При решении задач комбинаторики часто возникает необходимость в расчете биномиальных коэффициентов. Бином Ньютона, т.е. разложение 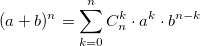 также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы:
также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: 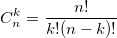 или использовать рекуррентную формулу:
или использовать рекуррентную формулу: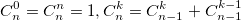 Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
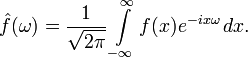
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Прямое преобразование:
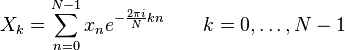
Обратное преобразование:
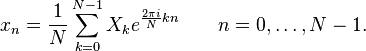
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
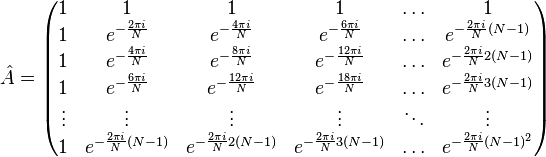
Согласно определению, свёрткой двух функций F и G называется функция FхG:
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
Где
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Рассмотрим полином F(x)=1+x и его свёртку с самим собой n раз
Fx..xF = SUM С( i, n-1 )*x^i = BFT ( FFT(F)*...*FFT(F) ) = BFT ( FFT(F)^(n-1) )
То есть биномиальные коэффициенты С( i, n-1 ) могут быть получены из значений коэффициентов полинома (1+x)^(n-1)
При вычислении с помощью треугольника Паскаля трудоёмкость имеет оценку O(n^2).
При вычислении с помощью быстрых Фурье-преобразований трудоёмкость имеет оценку O(n*log n).
В статье заимствованы фрагменты из статьи Расчет биномиальных коэффициентов на Си (С++)
P.S.
Трудоёмкость расчета биномиальных коэффициентов может быть уменьшена до O(n):
Cn[0]=1
Cn[i+1] = Cn[i]*(n-i)/(i+1)
Доказательство:
Cn[i]*(n-i)/(i+1) = n!/((n-i)!i!) * (n-i)/(i+1) = n!/((n-i-1)!(i+1)!) = Cn[i+1]
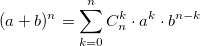 также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы:
также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: 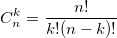 или использовать рекуррентную формулу:
или использовать рекуррентную формулу: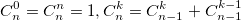 Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.
Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа. Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
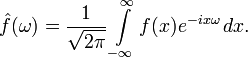
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Дискретное преобразование Фурье
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы дискретных преобразований
Прямое преобразование:
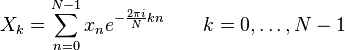
Обратное преобразование:
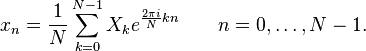
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
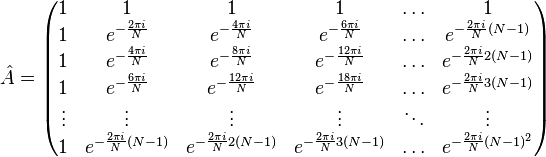
Свёртка двух функций
Согласно определению, свёрткой двух функций F и G называется функция FхG:
FхG(t) = SUM F(i)*G(j)|i+j=t
Фурье-преобразования для вычисления свёртки
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
FхG = BFT ( FFT(F)*FFT(G) )
Где
- FFT – операция прямого преобразования Фурье
- BFT – операция обратного преобразования Фурье
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Биномиальные коэффициенты
Рассмотрим полином F(x)=1+x и его свёртку с самим собой n раз
Fx..xF = SUM С( i, n-1 )*x^i = BFT ( FFT(F)*...*FFT(F) ) = BFT ( FFT(F)^(n-1) )
То есть биномиальные коэффициенты С( i, n-1 ) могут быть получены из значений коэффициентов полинома (1+x)^(n-1)
Программируем:
using System;
using System.Drawing;
using System.Linq;
using System.Numerics;
namespace FFTTools
{
public class BinomialBuilder : BuilderBase, IBuilder
{
/// <summary>
/// Performs application-defined tasks associated with freeing, releasing, or resetting unmanaged resources.
/// </summary>
public void Dispose()
{
}
public static void GetLongs(long[] array, long x = 1)
{
var n = array.Length - 1;
if (array.Length > 0) array[0] = 1;
for (var i = 0; i < n; i++)
array[i + 1] = x*array[i]*(n - i)/(i + 1);
}
public static void GetDoubles(double[] array, double x = 1.0)
{
var complex = new Complex[array.Length];
if (array.Length > 0) complex[0] = Complex.One;
if (array.Length > 1) complex[1] = x;
if (array.Length > 0)
{
Fourier(complex, FourierDirection.Forward);
complex = complex.Select(
value => Complex.Pow(value, array.Length - 1)/array.Length).ToArray();
Fourier(complex, FourierDirection.Backward);
}
var index = 0;
foreach (var value in complex) array[index++] = value.Real;
}
public Bitmap ToBitmap(Bitmap source)
{
throw new NotImplementedException();
}
}
}
Проверяем:
using System;
using System.Linq;
using Microsoft.VisualStudio.TestTools.UnitTesting;
namespace FFTTools.UnitTest
{
[TestClass]
public class BinomialUnitTest
{
[TestMethod]
public void BinomialTestMethod()
{
const int count = 10;
var doubles = new double[count];
var longs = new long[count];
BinomialBuilder.GetLongs(longs);
BinomialBuilder.GetDoubles(doubles);
Console.WriteLine(
string.Join(Environment.NewLine,
longs.Zip(doubles, (x, y) => string.Format("{0} - {1} = {2}", x, y, x - y))) +
Environment.NewLine);
Assert.IsTrue(doubles.Zip(longs, (x, y) => x - y).All(x => Math.Abs(x) < 0.001));
}
}
}
Зачем?
При вычислении с помощью треугольника Паскаля трудоёмкость имеет оценку O(n^2).
При вычислении с помощью быстрых Фурье-преобразований трудоёмкость имеет оценку O(n*log n).
Примечание:
В статье заимствованы фрагменты из статьи Расчет биномиальных коэффициентов на Си (С++)
P.S.
Трудоёмкость расчета биномиальных коэффициентов может быть уменьшена до O(n):
Cn[0]=1
Cn[i+1] = Cn[i]*(n-i)/(i+1)
Доказательство:
Cn[i]*(n-i)/(i+1) = n!/((n-i)!i!) * (n-i)/(i+1) = n!/((n-i-1)!(i+1)!) = Cn[i+1]