В этой статье я хочу рассмотреть один, на мой взгляд, достойный внимания подход к фильтрации изображений методом математической морфологии. Про математическую морфологию написано много статей, и одна из них размещена здесь на хабре. Читателю, незнакомому с данной темой, я рекомендую сначала ознакомиться с материалом по ссылке выше.
В статье про фильтрацию изображения я рассказывал про метод фильтрации медианным фильтром. Данный фильтр показал себя очень даже неплохо, но у него есть ряд ограничений и неудобств:
громоздкий даже в реализации 3x3:
- требует формирование оконной функции
- очень сложен для расширения окна
- большое запаздывание (latency) при последовательном соединении с другими оконными функциями.
Все эти неудобства нисколько не умаляют степень его применимости в цифровых системах обработки изображений, однако существует и иной подход.
Фильтрация изображений при помощи математической морфологии — давно известная тема, и всё что я хочу, это чуть ближе познакомить читателя с ней.
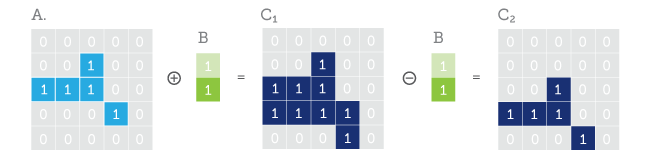
Как мы уже выяснили из статьи выше по тексту, из базовых морфологических операций сужение (erosion) и расширение (dilation) можно построить операции открытие (opening) и закрытие (closing).
Операция открытие — это последовательное выполнение erosion -> dilation. Такая комбинация приведёт к тому, что одиночные пиксели и малые их скопления будут безвозвратно сожраны сужением, как и крупные объекты подвергнутся обгладыванию ) по бокам. Если внутри больших объектов были маленькие дырки, то и они станут больше. Последующая операция расширения восстановит обглоданные объекты до первоначальных размеров, однако мелкого мусора, сожранного сужением уже не будет.
Операция закрытие — это последовательное выполнение dilation → erosion. Эта операция сначала заполнит дырки внутри объектов и сделает их чуть толще, а затем уменьшит их толщину до первоначальной, но дырок больше не будет.
Последовательное выполнение операций opening → closing является очень хорошим фильтром, ничем не хуже медианного, а напротив, она ещё и объекты сделает нам менее дырявыми. Обязательным условием является одинаковый размер окна для базовых операций.
Однако, каждая базовая операция erosion или dilation являет собой всё ту же оконную функцию, требующую как минимум 2 FIFO для реализации окна 3x3 и логические операции AND или OR в зависимости от функции.
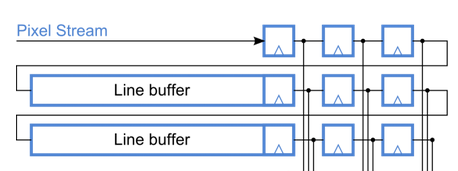
Для более глубокой фильтрации нередко применяют окно 5x5 и 7x7, что влечёт за собой увеличение объёма памяти на элементы FIFO и общее время запаздывания.
Для реализации подобных операций на ПЛИС фирмы Альтера можно использовать мегафункцию FIFO и встроенную 2-х портовую память, однако на одно такое FIFO шириной всего в 1 бит, а большего нам и не надо для бинаризованного изображения, уйдёт целый блок памяти, например M4K, что тоже не очень экономично.
Low complexity метод
Занимаясь поиском альтернативных решений, я наткнулся в сети на, так называемый, low complexity метод. Суть этого метода — декомпозиция матрицы оконной функции. Исходная матрица раскладывается на две:
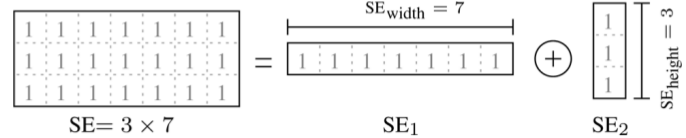
И работает согласно этому изображению:
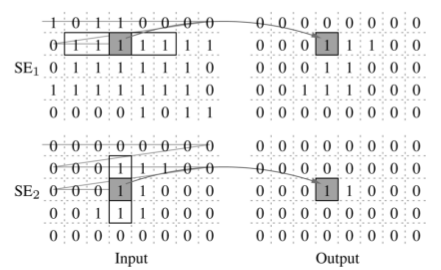
К моему стыду и сожалению, я не силён в математике и тему разложения матриц в ВУЗе я проходил, но только мимо. По этому, рассказывать как оно работает с математической точки зрения и почему именно так, а не иначе я не стану по понятным причинам.
В вышеупомянутой статье была представлена функциональная схема реализации операций erosion и dilation с применением low complexity метода. Данная схема состоит из двух блоков, каждый из которых олицетворяет структурный элемент SE1 и SE2.

Из данной схемы понятно, что выбор операций erosion/dilation выполняется инверсией входных данных т.к. эти операции симметричны.
Выход блока Stage-1 зависит от значения входного пикселя и накопленной суммы в триггере ff. Как только эта сумма станет равна ширине окна структурного элемента SE1, на выход блока пойдёт “1” иначе “0”. Любой “0” на входе блока сбрасывает накопленную сумму в триггере ff в ноль. Очевидно, что данный блок подсчитывает количество последовательно идущих единиц под структурным элементом SE1.
Выход блока Stage-1 поступает на вход блока Stage-2, который работает по такому-же принципу. Отличием его от блока Stage-1 является использование памяти Row_mem глубиной в количество столбцов входного изображения, и сумма хранится отдельно для каждого столбца в этой памяти. Выход блока “1” только тогда, когда сумма по столбцу равна высоте структурного элемента SE2. Выходной сигнал блока Stage-2 может быть проинвертирован в зависимости от выполняемой операции erosion или dilation.
Таким образом, получается что в блоке Stage-1 схема отслеживает все “1” под горизонтальным элементом SE1 и результат передаёт в блок Stage-2, который в свою очередь, отслеживает все “1” под вертикальным элементом SE2 учитывая результат выхода SE1.
Так же, в данной схеме предусмотрены сигналы, обеспечивающие работу структурного элемента SE на границах изображения.

Границы изображения условно обозначены названиями сторон света: North, South, West и East. При нахождении структурного элемента SE на границах изображения, предусмотрена вставка (padding) необходимого количества единиц или нулей, соответствующего половинному размеру структурного элемента.
Большим преимуществом этого метода является экономия памяти. Объем требуемой памяти для блоков Stage-1 и Stage-2 определяется размером слова (WL) равным
Log2(SE1_width) и Log2(SE2_height). Для блока Stage-2 используется не триггер, а память Row_mem, объём которой равен Image_width x Log2(SE2_height).
Очевидно, что результат вычисления логарифма надо округлить до ближайшего значения разрядности SE1_width и SE2_height, т.е. если окно 3x5, то округлённое значение Log2(SE1_width) = 2 бита, а Log2(SE2_height) = 3 бита.
Не сложно заметить, что разницы нет в использовании памяти для окна 3x3 в low complexity методе и обычном оконном. Что в первом случае объём памяти равен 320 столбцов x 2 бита, что во вторм: два однобитных элемента FIFO размером по 320 элементов. Если же размер окна меняется на 5x5 или 7x7, то количество FIFO растёт пропорционально количеству рядов окна, а вот для low complexity метода размер слова увеличится всего лишь на 1 бит, и память Row_mem станет не 320x2, а 320x3.
Таким образом, можно заранее заложить максимальный размер окна и использовать, например, мегафункцию altsyncram этого размера. Это будет куда экономичнее чем использование FIFO для формирования оконной функции.
Код модуля erosion/dilation на языке Verilog:
Low complexity erosion/dilation
module low_complexity
#(parameter BW = 3'd3,
parameter BH = 3'd3,
parameter WIDTH = 9'd320,
parameter HEIGH = 9'd240,
parameter START_X = 9'd320,
parameter START_Y = 9'h0
)
(
input wire clk,
input wire er_dil,
input wire [0:0] data_in,
input wire input_valid,
input wire [10:0] x_in, y_in,
output wire output_valid,
output wire [0:0] data_out
);
localparam END_X = (WIDTH + START_X) - 1;
localparam END_Y = HEIGH - 1;
wire e_bound, s_bound, n_bound, w_bound;
assign n_bound = (y_in == START_Y && x_in == START_X) ? 1'b1 : 1'b0;
assign s_bound = (y_in == END_Y && x_in == END_X) ? 1'b1 : 1'b0;
assign w_bound = (x_in == START_X) ? 1'b1 : 1'b0;
assign e_bound = (x_in == END_X) ? 1'b1 : 1'b0;
// stage 1
wire mux1_out, mux2_out;
wire [2:0] mux3_out;
wire [2:0] mux4_out;
reg [2:0] ff = 0;
reg [2:0] ff_d = 0;
wire [2:0] sum1;
wire [2:0] mux5_out;
wire cmp1_out;
wire [8:0] mem_addr = input_valid ? x_in[8:0] - START_X : 9'd0;
assign mux1_out = er_dil ? ~data_in : data_in;
assign mux2_out = (e_bound | s_bound) ? 1'b1 : mux1_out;
assign mux3_out = mux2_out ? sum1 : 3'h0;
assign mux4_out = cmp1_out ? mux5_out : mux3_out;
always @(posedge clk) ff_d = mux4_out;
always @* ff = ff_d;
assign mux5_out = w_bound ? BH - 1'b1 : ff;
assign sum1 = mux5_out + 1'b1;
assign cmp1_out = (mux3_out == BW) ? 1'b1 : 1'b0;
// stage2 2
wire [2:0] sum2;
wire [2:0] mux6_out, mux7_out;
wire cmp2_out;
wire [2:0] mux8_out;
wire [2:0] mem_out;
alt_ram320x3 row_mem (
.clock(clk),
.data(mux7_out),
.rdaddress(mem_addr),
.wraddress(mem_addr),
.wren(1'b1),
.q(mem_out)
);
assign mux6_out = cmp1_out ? sum2 : 3'h0;
assign mux7_out = cmp2_out ? mux8_out : mux6_out;
assign mux8_out = n_bound ? BW : mem_out;
assign sum2 = mux8_out + 1'b1;
assign cmp2_out = (mux6_out == BH) ? 1'b1 : 1'b0;
assign data_out = er_dil ? ~cmp2_out : cmp2_out;
assign output_valid = input_valid;
endmodule
Операции открытие и закрытие:
opening/closing
wire [0:0] er1_out, dil1_out, er2_out, dil2_out;
wire dil_input = line_data_out;
// OPENING
// EROSION 3x3
low_complexity
#(
.BW(3'h3), .BH(3'h3),
.WIDTH(9'd320), .HEIGH(9'd240),
.START_X(9'd320), .START_Y(9'h0)
) er_1 (
.clk(clk),
.er_dil(1'b0),
.data_in(dil_input),
.input_valid(line_rd_rq),
.x_in(x_in),
.y_in(y_in),
.output_valid(),
.data_out(er1_out)
);
// DILATION 3x3
low_complexity
#(
.BW(3'h3), .BH(3'h3),
.WIDTH(9'd320), .HEIGH(9'd240),
.START_X(9'd320), .START_Y(9'h0)
) dil_1 (
.clk(clk),
.er_dil(1'b1),
.data_in(er1_out),
.input_valid(line_rd_rq),
.x_in(x_in),
.y_in(y_in),
.output_valid(),
.data_out(dil1_out)
);
// CLOSING
// DILATION 3x3
low_complexity
#(
.BW(3'h3), .BH(3'h3),
.WIDTH(9'd320), .HEIGH(9'd240),
.START_X(9'd320), .START_Y(9'h0)
) dil_2 (
.clk(clk),
.er_dil(1'b1),
.data_in(dil1_out),
.input_valid(line_rd_rq),
.x_in(x_in),
.y_in(y_in),
.output_valid(),
.data_out(dil2_out)
);
// EROSION 3x3
low_complexity
#(
.BW(3'h3), .BH(3'h3),
.WIDTH(9'd320), .HEIGH(9'd240),
.START_X(9'd320), .START_Y(9'h0)
) er_2 (
.clk(clk),
.er_dil(1'b0),
.data_in(dil2_out),
.input_valid(line_rd_rq),
.x_in(x_in),
.y_in(y_in),
.output_valid(),
.data_out(er2_out)
);
Результат
На этом видео демонстрируется эффективность фильтрации изображения методом математической морфологии (low complexity method) с окном 3x3 в сравнении с медианным фильтром с окном того-же размера.
Зелёный маркер — медианный фильтр
Жёлтый маркер — морфология
Заметно, что на видео с зелёным маркером появляется неотфильтрованный мусор и детектор помещает его в рамку, а на видео с жёлтым маркером мусор исчезает и в рамку попадает только крупный объект.
Из этого эксперимента можно сделать вывод, что фильтр на основе математической морфологии справляется чуть лучше чем медианный.
Выводы
На основе метода low complexity erosion/dilation можно построить базовые элементы морфологической обработки изображения много эффективнее по расходу памяти чем при помощи формирования оконной функции.
Результат фильтрации изображения методом математической морфологии ничуть не хуже результата фильтрации медианным фильтром, и является неплохой альтернативой последнему.
Материалы по теме
→ Low complexity method
→ Morphological image processing
→ Математическая морфология





