Изображения формата JPEG встречаются повсюду в нашей цифровой жизни, но за этим покровом осведомлённости скрываются алгоритмы, устраняющие детали, не воспринимаемые человеческим глазом. В итоге получается высочайшее визуальное качество при наименьшем размере файла – но как конкретно всё это работает? Давайте посмотрим, чего именно не видят наши глаза!

Легко принять, как само собой разумеющееся, возможность отправить фотку другу, и не волноваться по поводу того, какое устройство, браузер или операционную систему он использует – однако так было не всегда. К началу 1980-х компьютеры умели хранить и показывать цифровые изображения, однако по поводу наилучшего способа для этого существовало множество конкурирующих идей. Нельзя было просто отправить изображение с одного компьютера на другой и надеяться, что всё заработает.
Для решения этой проблемы в 1986 году был собран комитет экспертов со всего мира под названием "Объединённая группа экспертов по фотографии" (Joint Photographic Experts Group, JPEG), основанный в рамках совместной работы Международной организации по стандартизации (ISO) и Международной электротехнической комиссии (IEC) – двух международных организаций по стандартизации, штаб-квартира которых расположена в Женеве (Швейцария).
Группа людей под названием JPEG создала стандарт сжатия цифровых изображений JPEG в 1992 году. Любой человек, использовавший интернет, вероятно, встречался с изображениями в кодировке JPEG. Это самый распространённый способ кодирования, отправки и хранения изображений. От веб-страниц до емейла и соцсетей, JPEG используется миллиарды раз в день – практически каждый раз, когда мы смотрим изображение онлайн или отправляем его. Без JPEG веб был бы менее ярким, более медленным, и, вероятно, в нём было бы меньше фоток котиков!
Эта статья – о том, как декодировать JPEG изображение. Иначе говоря, о том, что требуется для преобразования сжатых данных, хранящихся на компьютере, в изображение, появляющееся на экране. Об этом стоит знать не только потому, что это важно для понимания технологии, которую мы используем ежедневно, но и потому, что раскрывая уровни сжатия, мы лучше узнаём восприятие и зрение, а также то, к каким деталям наши глаза восприимчивей всего.
Кроме того, играться с изображениями таким способом очень интересно.
Заглядывая внутрь JPEG
На компьютере всё хранится в виде последовательности двоичных чисел. Обычно эти биты, нули и единицы, группируются по восемь, составляя байты. Когда вы открываете JPEG изображение на компьютере, что-то (браузер, операционка, ещё что-то) должно декодировать байты, восстановив изначальное изображение в виде списка цветов, которые можно показать.
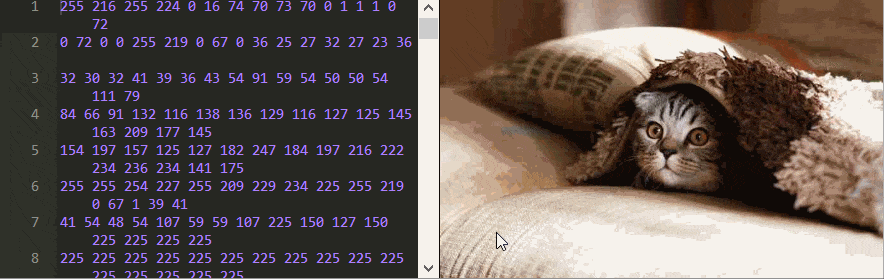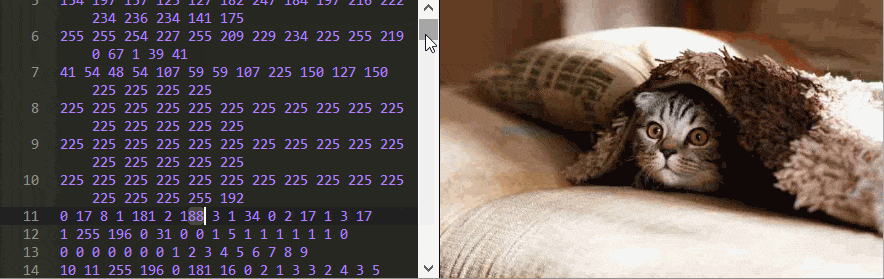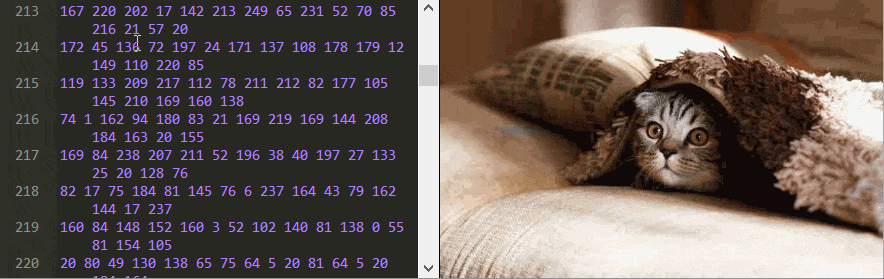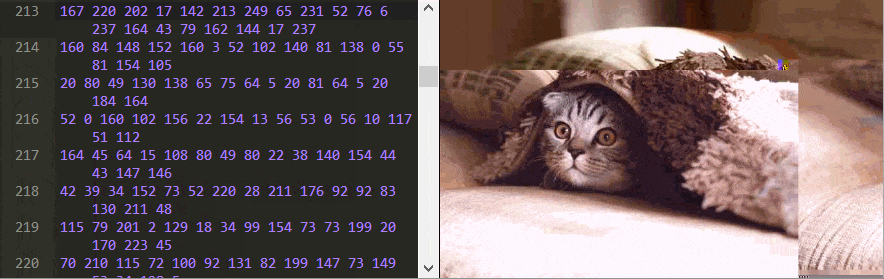
Если вы скачаете эту умильную фотографию кота и откроете её в текстовом редакторе, вы увидите кучу бессвязных символов.

Здесь я использую Notepad++ для изучения содержимого файла, поскольку обычные текстовые редакторы, типа Notepad из Windows, испортят двоичный файл после сохранения, и он перестанет удовлетворять формату JPEG.
Открывая изображение в текстовом редакторе, вы сбиваете компьютер с толку, точно так же, как вы сбиваете с толку свой мозг, когда потрёте глаза и начинаете видеть цветные пятна!
Эти пятна, которые вы видите, известны, как фосфены, и не являются результатом воздействия светового стимула или галлюцинациями, порождёнными разумом. Они возникают, потому что ваш мозг считает, что любые электрические сигналы в глазных нервах передают информацию о свете. Мозгу необходимо делать такие предположения, поскольку никак нельзя узнать, является ли сигнал звуком, видением или чем-то ещё. Все нервы в теле передают абсолютно одинаковые электрические импульсы. Давя на глаза, вы отправляете сигналы, не являющиеся зрительными, но активирующие рецепторы глаза, что ваш мозг интерпретирует – в данном случае, неверно – как нечто зрительное. Вы буквально способны видеть давление!
Забавно думать о том, насколько компьютеры похожи на мозг, однако это также является полезной аналогией, иллюстрирующей, насколько сильно значение данных – передаваемых по телу нервами, или хранящихся на компьютере – зависит от их интерпретации. Все двоичные данные состоят из нулей и единиц, базовых компонентов, способных передавать информацию любого вида. Ваш компьютер часто догадывается, как интерпретировать их при помощи подсказок, например, расширений файлов. А сейчас мы заставляем его интерпретировать их как текст, поскольку именно этого ожидает текстовый редактор.
Чтобы понять, как декодировать JPEG, нам нужно увидеть сами изначальные сигналы – двоичные данные. Это можно сделать при помощи шестнадцатеричного редактора, или же прямо на веб-странице оригинала статьи! Там есть изображение, рядом с которым в текстовом поле приведены все его байты (кроме заголовка), представленные в десятичном виде. Вы можете менять их, и скрипт перекодирует и выдаст новое изображение на лету.

Можно узнать многое, просто играясь с этим редактором. К примеру, можете ли вы сказать, в каком порядке хранятся пиксели?
В этом примере странно то, что изменение некоторых чисел вообще не влияет на изображение, а, например, если заменить число 17 на 0 в первой строке, то фотка полностью испортится!

Другие изменения, например, замена 7 на строке 1988 на число 254 изменяет цвет, но только последующих пикселей.

Возможно, наиболее странным будет то, что некоторые числа меняют не только цвет, но и форму изображения. Измените 70 в строке 12 на 2 и посмотрите на верхний ряд изображения, чтобы увидеть, что я имею в виду.

И вне зависимости от того, какое JPEG изображение вы используете, вы всегда будете находить эти загадочные шахматные последовательности при редактировании байтов.
Играясь с редактором, тяжело понять, как воссоздаётся фотка из этих байтов, поскольку JPEG сжатие состоит из трёх различных технологий, применяющихся последовательно по уровням. Мы изучим каждую из них отдельно, чтобы раскрыть наблюдаемое нами загадочное поведение.
Три уровня JPEG сжатия:
- Цветовая субдискретизация.
- Дискретное косинусное преобразование и дискретизация.
- Кодирование длин серий, дельта и Хаффмана
Дабы вы могли представить себе масштабы сжатия, обратите внимание, что изображение, приведённое выше, представляет 79 819 чисел, то есть, около 79 Кб. Если бы мы хранили его без сжатия, для каждого пикселя потребовалось бы по три числа – для красной, зелёной и синей составляющей. Это составило бы 917 700 чисел, или ок. 917 Кб. В результате JPEG сжатия итоговый файл уменьшился больше чем в 10 раз!
На самом деле, это изображение можно сжать гораздо сильнее. Снизу приведены два изображения рядом – фотка справа была ужата до 16 Кб, то есть в 57 раз меньше, чем несжатая версия!

Если присмотреться, будет видно, что эти изображения не идентичны. Оба они – картинки с JPEG сжатием, однако правая гораздо меньше по объёму. Также она выглядит чуть похуже (посмотрите на квадраты цветов фона). Поэтому JPEG ещё называют сжатием с потерями; в процессе сжатия изображение меняется и теряет некоторые детали.
1. Цветовая субдискретизация
Вот изображение с применением только первого уровня сжатия.

(Интерактивная версия – в оригинале статьи). Удаление одного числа рушит все цвета. Однако если удалить ровно шесть чисел, это практически не влияет на изображение.
Теперь числа чуть проще расшифровать. Это почти что простой список цветов, у которого каждый байт изменяет ровно один пиксель, но при этом он уже в два раза меньше несжатого изображения (которое занимало бы ок. 300 Кб в таком уменьшенном размере). Догадаетесь, почему?
Можно видеть, что эти числа не обозначают стандартные красную, зелёную и синюю компоненты, поскольку если заменить все числа нулями, мы получим зелёное изображение (а не белое).

Это потому, что эти байты обозначают Y (яркость),

Cb (относительная голубизна),

и Cr (относительная краснота) картинки.

Почему не использовать RGB? Ведь именно так работает большинство современных экранов. Ваш монитор может демонстрировать любой цвет, включая красный, зелёный и синий цвета с разной интенсивностью для каждого пикселя. Белый получается включением всех трёх на полную яркость, а чёрный – их отключением.
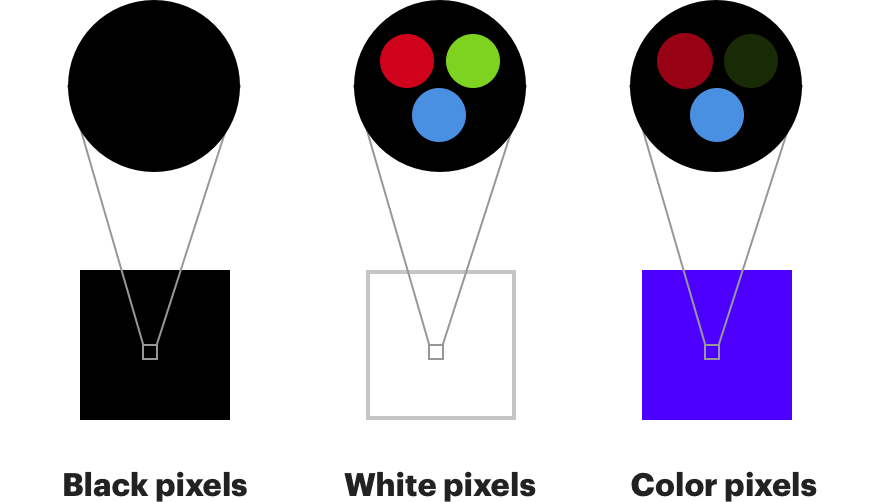
Это также очень похоже на работу человеческого глаза. Цветовые рецепторы наших глаз называются "колбочки", и делятся на три типа, каждый из которых более чувствителен либо к красному, либо к зелёному, либо к синему цветам [колбочки S-типа чувствительны в фиолетово-синей (S от англ. Short — коротковолновый спектр), M-типа — в зелено-желтой (M от англ. Medium — средневолновый), и L-типа — в желто-красной (L от англ. Long — длинноволновый) частях спектра. Наличие этих трёх видов колбочек (и палочек, чувствительных в изумрудно-зелёной части спектра) даёт человеку цветное зрение. / прим. перев.]. Палочки, другой тип фоторецепторов в наших глазах, способны улавливать только изменения в яркости, однако они гораздо более чувствительные. В наших глазах есть около 120 млн палочек и всего 6 млн колбочек.
Поэтому наши глаза гораздо лучше замечают изменения в яркости, чем изменения в цвете. Если отделить цвет от яркости, можно убрать немного цвета, и никто ничего не заметит. Цветовая субдискретизация – это процесс представления цветовых компонентов изображения в меньшем разрешении по сравнению с компонентами яркости. В примере выше у каждого пикселя ровно один компонент Y, а у каждой отдельной группы из четырёх пикселей есть ровно одна компонента Cb и одна Cr. Поэтому изображение содержит в четыре раза меньше цветовой информации, чем было у оригинала.
Цветовое пространство YCbCr используется не только в JPEG. Его изначально придумали в 1938 году для телепередач. Не у всех есть цветной телевизор, поэтому разделение цвета и яркости позволило всем получать один и тот же сигнал, а телевизоры без цвета просто использовали только компонент яркости.
Поэтому удаление одного числа из редактора полностью рушит все цвета. Компоненты хранятся в виде Y Y Y Y Cb Cr (на самом деле, не обязательно в таком порядке – порядок хранения задаётся в заголовке файла). Удаление первого числа приведёт к тому, что первое значение Cb будет воспринято, как Y, Cr как Cb, и в целом получится эффект домино, переключающий все цвета картинки.
Спецификация JPEG не обязывает вас использовать YCbCr. Но в большинстве файлов она используются, поскольку она даёт изображения лучшего качества после субдискретизации по сравнению с RGB. Но вам не обязательно верить мне на слово. Посмотрите сами в табличке ниже, как будет выглядеть субдискретизация каждого отдельного компонента как в RGB, так и в YCbCr.

(Интерактивная версия – в оригинале статьи).
Удаление синего не так заметно, как красного или зелёного. Всё потому, что из шести миллионов колбочек в ваших глазах около 64% чувствительны к красному, 32% к зелёному и 2% к синему.
Субдискретизация компонента Y (слева внизу) видна лучше всего. Заметно даже небольшое изменение.
Преобразование изображения из RGB в YCbCr не уменьшает размер файла, но облегчает поиск менее заметных деталей, которые можно удалить. Сжатие с потерями происходит на втором этапе. В её основе лежит идея представления данных в более сжимаемом виде.
2. Дискретное косинусное преобразование и дискретизация
Этот уровень сжатия по большей части и определяет суть JPEG. После преобразования цветов в YCbCr компоненты сжимаются по отдельности, поэтому далее мы можем сконцентрироваться только на компоненте Y. И вот как выглядят байты компонента Y после применения этого уровня.
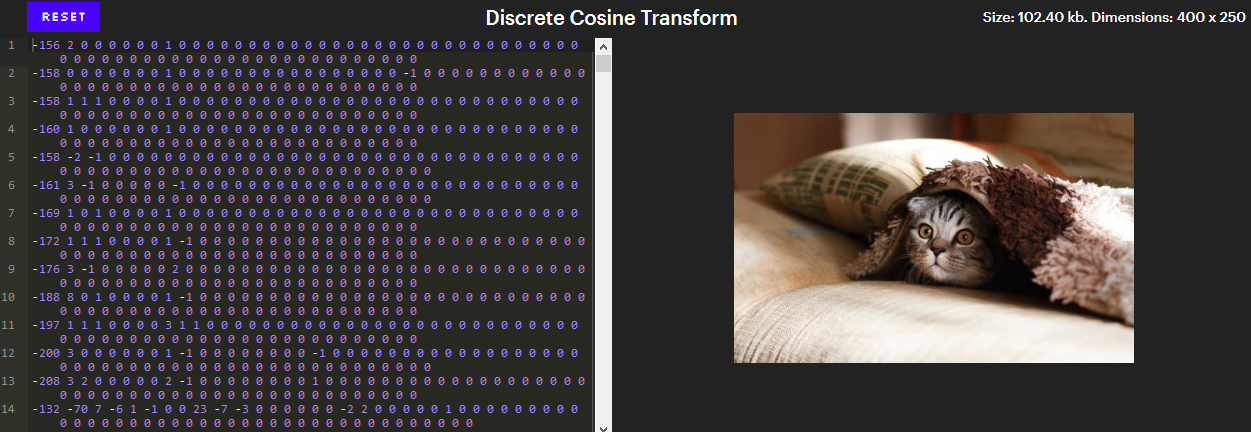
(Интерактивная версия – в оригинале статьи). В интерактивной версии клик на пикселе прокручивает редактор на строчку, которая его обозначает. Попробуйте поудалять числа с конца или добавить несколько нулей к определённому числу.
На первый взгляд, выглядит, как очень плохое сжатие. В изображении 100 000 пикселей, и для обозначения их яркости (Y-компоненты) требуется 102 400 чисел — это хуже, чем если вообще ничего не сжимать!
Однако обратите внимание на то, что большинство этих чисел равны нулю. Более того, все эти нули в конце строк можно удалять, не меняя изображение. Остаётся порядка 26 000 чисел, а это уже почти в 4 раза меньше!
На этом уровне находится секрет шахматных узоров. В отличие от других эффектов, которые мы видели, появление этих узоров не является глюком. Они – строительные блоки всего изображения. В каждой строчке редактора содержится ровно 64 числа, коэффициенты дискретного косинусного преобразования (DCT), соответствующие интенсивностям 64-х уникальных узоров.
Эти узоры формируются на основе графика косинуса. Вот, как выглядят некоторые из них:

8 из 64 коэффициентов
Ниже – изображение, демонстрирующее все 64 узора.

(Интерактивная версия – в оригинале статьи).
Эти узоры имеют особое значение, поскольку они формируют базис изображений размера 8х8. Если вы незнакомы с линейной алгеброй, то это означает, что любое изображение размера 8х8 можно получить из этих 64-х узоров. DCT – это процесс разбиения изображений на блоки 8х8 и преобразования каждого блока в комбинацию из этих 64 коэффициентов.
То, что любое изображение можно составить из 64 определённых узоров, кажется волшебством. Однако это то же самое, что сказать, что любое место на Земле можно описать двумя числами – широтой и долготой [с указанием полушарий / прим. перев.]. Мы часто считаем поверхность Земли двумерной, поэтому нам требуются всего два числа. Изображение 8х8 имеет 64 измерения, поэтому нам требуются 64 числа.
Пока непонятно, как это помогает нам в смысле сжатия. Если нам нужно 64 числа для представления изображения 8х8, почему этот способ будет лучше, чем просто хранить 64 компоненты яркости? Мы делаем это по той же причине, по которой мы превратили три числа RGB в три числа YCbCr: это позволяет нам удалить незаметные детали.
Сложно увидеть, какие именно детали удаляются на этом этапе, поскольку JPEG применяет DCT к блокам 8х8. Однако никто не запрещает нам применить его к целой картинке. Вот, как выглядит DCT по компоненте Y в применении к целой картинке:

С конца можно удалить более 60 000 чисел практически без заметных изменений на фотке.

Однако отметьте, что если мы обнулим первые пять чисел, разница будет очевидной.

Числа в начале обозначают изменения низкой частоты в изображении, и наши глаза улавливают их лучше всего. Числа ближе к концу обозначают изменения высоких частот, которые сложнее заметить. Чтобы «увидеть то, что не видно глазом», мы можем изолировать эти детали высокой частоты, обнулив первые 5000 чисел.

Мы видим все области изображения, в которых происходит наибольшее изменение от пикселя к пикселю. Выделяются глаза кота, его усы, махровое одеяло и тени в нижнем левом углу. Можно пойти и дальше, обнулив первые 10 000 чисел:

20 000:

40 000:

60 000:

Эти высокочастотные детали JPEG и удаляет на этапе сжатия. Преобразование цветов в коэффициенты DCT не несёт потерь. Потери образуются на шаге дискретизации, где удаляются величины высокой частоты или близкие к нулю. Когда вы понижаете качество сохранения JPEG, программа увеличивает порог количества удаляемых значений, что даёт уменьшение размера файла, но делает картинку более пикселизированной. Поэтому изображение в первом разделе, которое было в 57 раз меньше, так выглядело. Каждый блок 8х8 представлялся гораздо меньшим количеством коэффициентов DCT по сравнению с более качественной версией.
Можно сделать такой крутой эффект, как постепенная потоковая передача изображений. Можно вывести размытую картинку, которая становится всё более детализированной по мере скачивания всё большего количества коэффициентов.
Вот, просто для интереса, что получится при использовании всего 24 000 чисел:

Или всего 5000:

Очень размыто, но как будто узнаваемо!
3. Кодирование длин серий, дельта и Хаффмана
Пока что все этапы сжатия шли с потерями. Последний этап, наоборот, идёт без потерь. Он не удаляет информацию, однако значительно уменьшает размер файла.
Как можно сжать что-либо, не отбрасывая информацию? Представьте, как бы мы описали простой чёрный прямоугольник 700 х 437.
JPEG использует для этого 5000 чисел, но можно достичь гораздо лучшего результата. Можете представить себе схему кодирования, которая бы описывала подобное изображение как можно меньшим количеством байт?
Минимальная схема, которую смог придумать я, использует четыре: три для обозначения цвета, и четвёртый – сколько пикселей имеет такой цвет. Идея представления повторяющихся значений таким сжатым способом называется кодирование длин серий. Она не имеет потерь, поскольку мы можем восстановить закодированные данные в первозданном виде.
Размер файла JPEG с чёрным прямоугольником гораздо больше 4 байт – вспомните, что на уровне DCT сжатие применяется к блокам 8х8 пикселей. Поэтому как минимум нам нужен один коэффициент DCT на каждые 64 пикселя. Один нам нужен потому, что вместо того, чтобы хранить один DCT-коэффициент, за которым идёт 63 нуля, кодирование длин серий позволяет нам хранить одно число и обозначить, что «все остальные – нули».
Дельта-кодирование – это техника, при которой каждый байт содержит отличие от какого-то значения, а не абсолютную величину. Поэтому редактирование определённых байтов изменяет цвет всех остальных пикселей. К примеру, вместо того, чтобы хранить
12 13 14 14 14 13 13 14
Мы могли бы начать с 12, а потом просто обозначать, сколько надо прибавить или отнять, чтобы получить следующее число. И эта последовательность в дельта-кодировании приобретает вид:
12 1 1 0 0 -1 0 1
Преобразованные данные не получаются меньше исходных, но сжимать их уже легче. Применение дельта-кодирования перед кодированием длин серий может сильно помочь, оставаясь при этом сжатием без потерь.
Дельта-кодирование – одна из немногих техник, применяемых вне блоков 8х8. Из 64 коэффициентов DCT один – просто постоянная волновая функция (сплошной цвет). Он представляет среднюю яркость каждого блока для компонент яркости, или среднюю голубизну для компонентов Cb, и так далее. Первое значение каждого DCT-блока называется DC-значением, и каждое DC-значение проходит дельта-кодирование по отношению к предыдущим. Поэтому изменение яркости первого блока повлияет на все блоки.
Остаётся последняя загадка: как изменение единственного числа полностью портит всю картинку? Пока таких свойств у уровней сжатия не было. Ответ лежит в заголовке JPEG. Первые 500 байт содержат метаданные об изображении – ширину, высоту, и проч., и пока мы с ними не работали.
Без заголовка практически невозможно (ну, или очень сложно) декодировать JPEG. Это будет выглядеть так, будто я пытаюсь описать вам картину, и начинаю изобретать слова для того, чтобы передать своё впечатление. Описание будет, вероятно, весьма сжатым, поскольку я могу изобретать слова именно с тем значением, которое я хочу передать, однако для всех остальных они не будут иметь смысла.
Звучит глупо, но именно так это и происходит. Каждое изображение JPEG сжимается с кодами, специфичными именно для него. Словарь кодов хранится в заголовке. Эта техника называется «код Хаффмана», а словарь – таблицей Хаффмана. В заголовке таблица отмечена двумя байтами – 255 и потом 196. У каждого цветового компонента может быть своя таблица.
Изменения таблиц радикально повлияют на любое изображение. Хороший пример – поменять на 15-й строке 1 на 12.

Это происходит потому, что в таблицах указывается, как нужно читать отдельные биты. Пока что мы работали только с двоичными числами в десятичном виде. Но это скрывает от нас тот факт, что если вы хотите хранить число 1 в байте, то оно будет выглядеть, как 00000001, поскольку в каждом байте должно быть ровно восемь бит, даже если нужен из них всего один.
Потенциально это большая трата места, если у вас есть много мелких чисел. Код Хаффмана – это техника, позволяющая нам ослабить это требование, по которому каждое число должно занимать восемь бит. Это значит, что если вы видите два байта:
234 115
То, в зависимости от таблицы Хаффмана, это могут быть три числа. Чтобы их извлечь, вам надо сначала разбить их на отдельные биты:
11101010 01110011
Затем обращаемся к таблице, чтобы понять, как их группировать. К примеру, это могут быть первые шесть битов, (111010), или 58 в десятичной системе, за которыми идут пять битов (10011), или 19, и наконец последние четыре бита (0011), или 3.
Поэтому очень сложно разобраться в байтах на этом этапе сжатия. Байты не представляют то, что кажется. Не буду углубляться в детали работы с таблицей в данной статье, но материалов по этому вопросу в сети достаточно.
Один из интересных трюков, которые можно проделать, зная это – отделить заголовок от JPEG и хранить его отдельно. По сути, получится, что файл сможете прочесть только вы. Facebook проделывает это, чтобы ещё сильнее уменьшать файлы.
Что ещё можно сделать – совсем немного изменить таблицу Хаффмана. Для других это будет выглядеть, как испорченная картинка. И только вы будете знать волшебный вариант её исправления.
Подведём итоги: так что же нужно для декодирования JPEG? Необходимо:
- Извлечь таблицу (таблицы) Хаффмана из заголовка и декодировать биты.
- Извлечь коэффициенты дискретного косинусного преобразования для каждого компонента цвета и яркости для каждого блока 8х8, проведя обратные преобразования кодирования длин серий и дельты.
- Скомбинировать косинусы на основе коэффициентов, чтобы получить значения пикселей для каждого блока 8х8.
- Масштабировать компоненты цветов, если проводилась субдискретизация (эта информация есть в заголовке).
- Преобразовать полученные значения YCbCr для каждого пикселя в RGB.
- Вывести изображение на экран!
Серьёзная работа для простого просмотра фотки с котиком! Однако, что мне в этом нравится – видно, насколько технология JPEG человекоцентрична. Она основана на особенностях нашего восприятия, позволяющих достичь гораздо лучшего сжатия, чем обычные технологии. И теперь, понимая, как работает JPEG, можно представить, как эти технологии можно перенести в другие области. К примеру, дельта-кодирование в видео может дать серьёзное уменьшение размера файла, поскольку там часто есть целые области, не меняющиеся от кадра к кадру (к примеру, фон).
Код, использованный в статье, открыт, и содержит инструкции по замене картинок на свои собственные.