Содержание:
В предыдущем разделе мы оценивали градиент путем исследования выходного значения схемы по каждому исходному значению по отдельности. Эта процедура дает нам то, что мы называем числовым градиентом. Однако этот подход все равно считается довольно проблематичным, так как нам нужно вычислять результат схемы по мере изменения каждого исходного значения на небольшое число. Поэтому сложность оценки градиента является линейной по количеству исходных значений. Но на практике у нас будут сотни, тысячи или (для нейронных сетей) от десятков до сотен миллионов исходных значений, и схемы будут включать не только один логический элемент умножения, но и огромные выражения, которые могут быть очень сложными в вычислении. Нам нужно что-то получше.
К счастью, существует более простой и значительно более быстрый способ вычисления градиента: мы можем использовать метод расчета для производной прямого выражения, который будет таким же простым в оценке, как и выходное значение схемы. Мы называем это аналитическим градиентом, и здесь не нужно что-то подставлять. Вы наверняка видели, как другие люди, обучающие нейронные сети, берут производные градиентов с помощью огромных и, четно говоря, страшных и сложных математических уравнений (если вы не особо сильны в математике). Но это необязательно. Я написал огромное количество кода для нейронных сетей и мне редко приходится брать математические производные длиной более двух строк, и в 95% случаев это можно сделать без необходимости что-то писать вообще. Это все потому, что мы вряд ли будем брать производную градиента для очень маленьких и простых выражений (считайте это базовым случаем), и потом я покажу вам, как можно довольно просто составлять такие выражения с помощью цепного правила для оценки целого градиента (считайте это индуктивным/рекурсивным случаем).
Если вы помните правила произведения, правила возведения в степень, правила частного (см. правила производных или страницу Википедии), вам будет просто записать производную по отношению к x и y для небольших выражений вроде x * y. Но предположим, что вы не помните правила дифференциального вычисления. Мы можем вернуться к определению. Например, вот выражение производной по отношению к x:

(Технически я не пишу предел в виде h стремящегося к нулю. Простите меня, математики). Хорошо. А теперь давайте включим нашу функцию ( f(x,y)=xy ) в выражение. Готовы к самой сложной математической части во всей этой статье? Вот она:
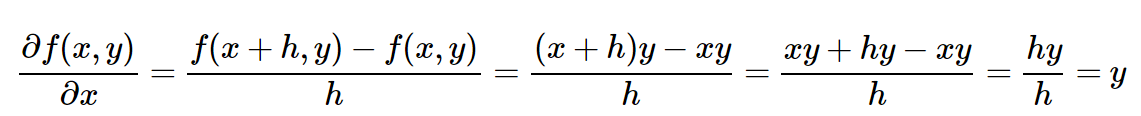
Это интересно. Производная по отношению к x просто равна y. Вы заметили совпадение с предыдущим разделом? Мы изменили x на x+h и вычислили x_derivative = 3.0, который, на самом деле, оказывается значением y в этом примере. Оказывается, что это не было совпадение как таковое, так как это всего лишь то, как, по мнению аналитического градиента, должна выглядеть производная x для f(x,y) = x * y. Производная по отношению к y, тем не менее, оказывается равной x, что неудивительно. Поэтому нет необходимости что-либо подставлять! Мы воспользовались силой математики и теперь можем преобразовать наши расчеты производной в следующий код:
Чтобы рассчитать градиент, мы прошли от перебора схемы сотни раз (Стратегия №1) до количества итераций в два раза больше количества исходных значений (Стратегия №2), и до ее продвижения только один раз! И он становится ЕЩЕ лучше, так как более затратные стратегии (№1 и №2) дают только приблизительный градиент, тогда как №3 (наиболее быстрый способ на данный момент) дает точный градиент. Никаких приблизительных значений. Единственный минус – вы должны чувствовать себя уверенно в дифференциальных вычислениях.
Давайте вкратце повторим, что мы узнали:
ИСХОДНОЕ ЗНАЧЕНИЕ: Нам дана схема, некоторые исходные значения, и мы должны вычислить выходное значение.
ВЫХОДНОЕ ЗНАЧЕНИЕ: Мы заинтересованы в поиске небольших изменений каждого исходного значения (по отдельности), которые могут сделать выходное значение более высоким.
Стратегия №1: Один простой способ, который заключается в произвольном поиске небольших изменений исходных значений и отслеживании, какое значение приводит к наибольшему увеличению результата.
Стратегия №2: Мы увидели, что мы можем больше что касается вычисления градиента. Вне зависимости от того, насколько сложной является схема, числовой градиент является довольно простым (но относительно затратным по времени) в вычислениях. Мы вычисляем его путем прощупывания выходных значений схемы по мере подстановки исходных значений по одному.
Стратегия №3: В конечном итоге, мы поняли, что мы можем быть умнее и аналитически взять производную прямого выражения для получения аналитического градиента. Он похож на числовой градиент, но на данный момент является наиболее быстрым, а также не требует подстановки значений.
На практике, между прочим (и мы к этому еще раз вернемся чуть позже), все библиотеки нейронных сетей всегда вычисляют аналитический градиент, но правильность выполнения проверяется путем его сравнения с числовым градиентом. Это потому, что числовой градиент очень прост в оценке (но он может быть немного затратным по времени при вычислении), в то время как аналитический градиент может иногда содержать ошибки, но он обычно довольно эффективен в вычислении. Как мы увидим далее, оценка градиента (т.е. в процессе выполнения обратного распространения ошибки или обратного прохода), оказывается, имеет такое же значение, как и оценка прямого прохода.
Глава 1: Схемы реальных значений
Часть 1:
Часть 2:
Часть 3:
Часть 4:
Часть 5:
Часть 6:
Введение
Базовый сценарий: Простой логический элемент в схеме
Цель
Стратегия №1: Произвольный локальный поиск
Часть 2:
Стратегия №2: Числовой градиент
Часть 3:
Стратегия №3: Аналитический градиент
Часть 4:
Схемы с несколькими логическими элементами
Обратное распространение ошибки
Часть 5:
Шаблоны в «обратном» потоке
Пример "Один нейрон"
Часть 6:
Становимся мастером обратного распространения ошибки
Глава 2: Машинное обучение
В предыдущем разделе мы оценивали градиент путем исследования выходного значения схемы по каждому исходному значению по отдельности. Эта процедура дает нам то, что мы называем числовым градиентом. Однако этот подход все равно считается довольно проблематичным, так как нам нужно вычислять результат схемы по мере изменения каждого исходного значения на небольшое число. Поэтому сложность оценки градиента является линейной по количеству исходных значений. Но на практике у нас будут сотни, тысячи или (для нейронных сетей) от десятков до сотен миллионов исходных значений, и схемы будут включать не только один логический элемент умножения, но и огромные выражения, которые могут быть очень сложными в вычислении. Нам нужно что-то получше.
К счастью, существует более простой и значительно более быстрый способ вычисления градиента: мы можем использовать метод расчета для производной прямого выражения, который будет таким же простым в оценке, как и выходное значение схемы. Мы называем это аналитическим градиентом, и здесь не нужно что-то подставлять. Вы наверняка видели, как другие люди, обучающие нейронные сети, берут производные градиентов с помощью огромных и, четно говоря, страшных и сложных математических уравнений (если вы не особо сильны в математике). Но это необязательно. Я написал огромное количество кода для нейронных сетей и мне редко приходится брать математические производные длиной более двух строк, и в 95% случаев это можно сделать без необходимости что-то писать вообще. Это все потому, что мы вряд ли будем брать производную градиента для очень маленьких и простых выражений (считайте это базовым случаем), и потом я покажу вам, как можно довольно просто составлять такие выражения с помощью цепного правила для оценки целого градиента (считайте это индуктивным/рекурсивным случаем).
Аналитическая производная не требует подстановок исходных значений. Эту производную можно взять с помощью математики (дифференциальных вычислений).
Если вы помните правила произведения, правила возведения в степень, правила частного (см. правила производных или страницу Википедии), вам будет просто записать производную по отношению к x и y для небольших выражений вроде x * y. Но предположим, что вы не помните правила дифференциального вычисления. Мы можем вернуться к определению. Например, вот выражение производной по отношению к x:
(Технически я не пишу предел в виде h стремящегося к нулю. Простите меня, математики). Хорошо. А теперь давайте включим нашу функцию ( f(x,y)=xy ) в выражение. Готовы к самой сложной математической части во всей этой статье? Вот она:
Это интересно. Производная по отношению к x просто равна y. Вы заметили совпадение с предыдущим разделом? Мы изменили x на x+h и вычислили x_derivative = 3.0, который, на самом деле, оказывается значением y в этом примере. Оказывается, что это не было совпадение как таковое, так как это всего лишь то, как, по мнению аналитического градиента, должна выглядеть производная x для f(x,y) = x * y. Производная по отношению к y, тем не менее, оказывается равной x, что неудивительно. Поэтому нет необходимости что-либо подставлять! Мы воспользовались силой математики и теперь можем преобразовать наши расчеты производной в следующий код:
var x = -2, y = 3;
var out = forwardMultiplyGate(x, y); // до этого: -6
var x_gradient = y; // с помощью нашего сложного математического вывода, приведенного выше
var y_gradient = x;
var step_size = 0.01;
x += step_size * x_gradient; // -2.03
y += step_size * y_gradient; // 2.98
var out_new = forwardMultiplyGate(x, y); // -5.87. Больший результат!
Чтобы рассчитать градиент, мы прошли от перебора схемы сотни раз (Стратегия №1) до количества итераций в два раза больше количества исходных значений (Стратегия №2), и до ее продвижения только один раз! И он становится ЕЩЕ лучше, так как более затратные стратегии (№1 и №2) дают только приблизительный градиент, тогда как №3 (наиболее быстрый способ на данный момент) дает точный градиент. Никаких приблизительных значений. Единственный минус – вы должны чувствовать себя уверенно в дифференциальных вычислениях.
Давайте вкратце повторим, что мы узнали:
ИСХОДНОЕ ЗНАЧЕНИЕ: Нам дана схема, некоторые исходные значения, и мы должны вычислить выходное значение.
ВЫХОДНОЕ ЗНАЧЕНИЕ: Мы заинтересованы в поиске небольших изменений каждого исходного значения (по отдельности), которые могут сделать выходное значение более высоким.
Стратегия №1: Один простой способ, который заключается в произвольном поиске небольших изменений исходных значений и отслеживании, какое значение приводит к наибольшему увеличению результата.
Стратегия №2: Мы увидели, что мы можем больше что касается вычисления градиента. Вне зависимости от того, насколько сложной является схема, числовой градиент является довольно простым (но относительно затратным по времени) в вычислениях. Мы вычисляем его путем прощупывания выходных значений схемы по мере подстановки исходных значений по одному.
Стратегия №3: В конечном итоге, мы поняли, что мы можем быть умнее и аналитически взять производную прямого выражения для получения аналитического градиента. Он похож на числовой градиент, но на данный момент является наиболее быстрым, а также не требует подстановки значений.
На практике, между прочим (и мы к этому еще раз вернемся чуть позже), все библиотеки нейронных сетей всегда вычисляют аналитический градиент, но правильность выполнения проверяется путем его сравнения с числовым градиентом. Это потому, что числовой градиент очень прост в оценке (но он может быть немного затратным по времени при вычислении), в то время как аналитический градиент может иногда содержать ошибки, но он обычно довольно эффективен в вычислении. Как мы увидим далее, оценка градиента (т.е. в процессе выполнения обратного распространения ошибки или обратного прохода), оказывается, имеет такое же значение, как и оценка прямого прохода.