В этой статье мы поговорим о детерминистических кошельках, иерархической генерации ключей, а также о том, как это математически работает и в каких случаях это удобно применять на практике. Данный материал будет полезен специалистам, чья деятельность связана с платежными шлюзами, Биткоин кошельками и другими хранилищами монет. Кроме того, материал будет интересен тем, кто увлекается эллиптической криптографией и схемами развертывания ключей электронной подписи.
В первую очередь давайте определим, что такое детерминистический кошелек (deterministic wallet). Когда мы говорим о генерации ключей, мы часто употребляем слово “кошелек”, потому что в контексте криптовалют владение личным ключом является доказательством владения монетами, а в данном случае кошелек и ключ имеют похожий смысл.
Deterministic wallet — это кошелек, в котором все используемые личные ключи были порождены из одного общего для всех ключей секрета. Особенность состоит в том, что есть возможность из одного секрета породить сколько-угодно пар ключей для электронной подписи. Можно использовать новые адреса для каждого входящего платежа и сдачи.
Удобно, что ключи такого кошелька можно легко перенести на другое устройство, сделать резервную копию и потом восстановить, потому что фактически нужно резервировать только один основной секрет. Кроме того, все порожденные из основного секрета личные ключи, друг с другом никак не связаны. Нельзя проследить и связь между порожденными адресами (определить что все они принадлежат одному пользователю), а имея порожденный личный ключ, нельзя восстановить общий секрет.
Теперь поговорим о кодировании основного секрета. Здесь имеется некоторый стандартизированный подход, который был определен в BIP39. Это так называемое Check Encoding кодирование основного секрета в мнемоническую фразу — набор слов, который легко записать на бумагу и при необходимости запомнить. При вводе есть возможность проверить контрольную сумму, то есть выявить ошибку, если такая имеется, с довольно большой вероятностью.
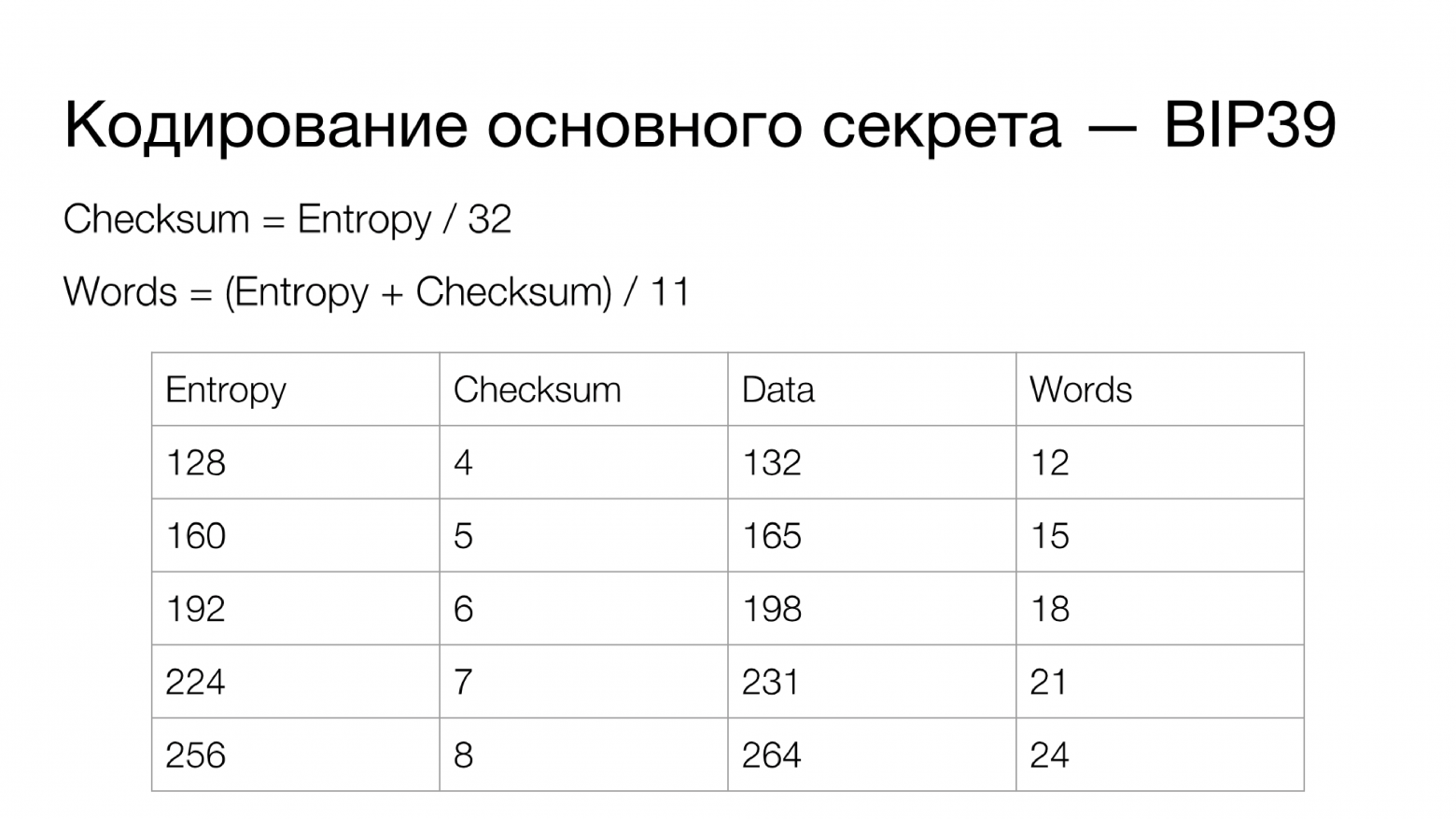
Как это работает? Фактически у вас есть основной секрет (Entropy) — данные, из которых разворачиваются все личные ключи кошелька. Этот секрет может иметь разную длину. Что касается контрольной суммы: на каждые 32 бита Entropy приходится 1 бит контрольной суммы, то есть Checksum по формуле рассчитывается, как длина Entropy в битах, разделенная на 32.
Entropy конкатенируется с контрольной суммой, которая рассчитывается, как двойной хеш SHA-256 (SHA-2 на длине 256 бит), после чего отрезается необходимое количество битов. Конкатенированные данные переводятся в другую систему счисления: из двоичной в систему счисления по основанию 2048 (как видим, 2048 — это ). И если сложить длину битов Entropy и контрольной суммы, то получится число, кратное 11-ти. Таким образом, мы получаем количество слов в выходной мнемонической фразе.
). И если сложить длину битов Entropy и контрольной суммы, то получится число, кратное 11-ти. Таким образом, мы получаем количество слов в выходной мнемонической фразе.
Фактически данные “нарезаются” частями по 11 бит. Есть словарь, состоящий из 2048 слов ( ), к которым применены определенные требования. По умолчанию язык словаря английский, но может использоваться любой. Слова не должны превышать определенную длину (обычно предел до 7 символов). Все они должны быть закодированы в UTF-8 с определенной нормализацией всех символов. Обязательной является уникальность каждого слова по первым четырем символам.
), к которым применены определенные требования. По умолчанию язык словаря английский, но может использоваться любой. Слова не должны превышать определенную длину (обычно предел до 7 символов). Все они должны быть закодированы в UTF-8 с определенной нормализацией всех символов. Обязательной является уникальность каждого слова по первым четырем символам.
Первые четыре символа однозначно определяют слово в словаре, а остальные символы используются, чтобы завершить это слово до удобной формы для чтения, запоминания и т. д. Таким образом каждый фрагмент данных, состоящий из 11-ти бит, получает однозначное соответствие в виде слова из словаря. Если Entropy вашего секрета составляет 256 бит, то данные для кодирования составят 264 бита, а ваша мнемоническая фраза будет содержать 24 слова. Это основной подход к кодированию секрета кошельков в BIP39, который применяется на практике чаще всего.
Для того чтобы в будущем делать резервную копию и использовать ее, вам предлагается выписать эту фразу на внешний носитель. Лучше всего подойдет бумага, которую вы будете хранить в надежном месте. Так вы можете восстановить полный доступ ко всем своим ключам.
Детерминистические кошельки бывают двух типов. Рассмотрим основные их отличия.
Первый из них самый простой. Основной секрет здесь конкатенируется с индексом дочернего ключа, который мы хотим получить, после чего конкатенированные данные хешируются. Чаще всего это происходит с помощью хеш-функции SHA-256.
Ко второму типу относятся иерархические детерминистические кошельки (hierarchical deterministic wallets, HD wallets), принципы которых определены в BIP32, и являются очень распространенным подходом к иерархической генерации ключей.
Рассмотрим отличия этих типов кошельков на схеме.
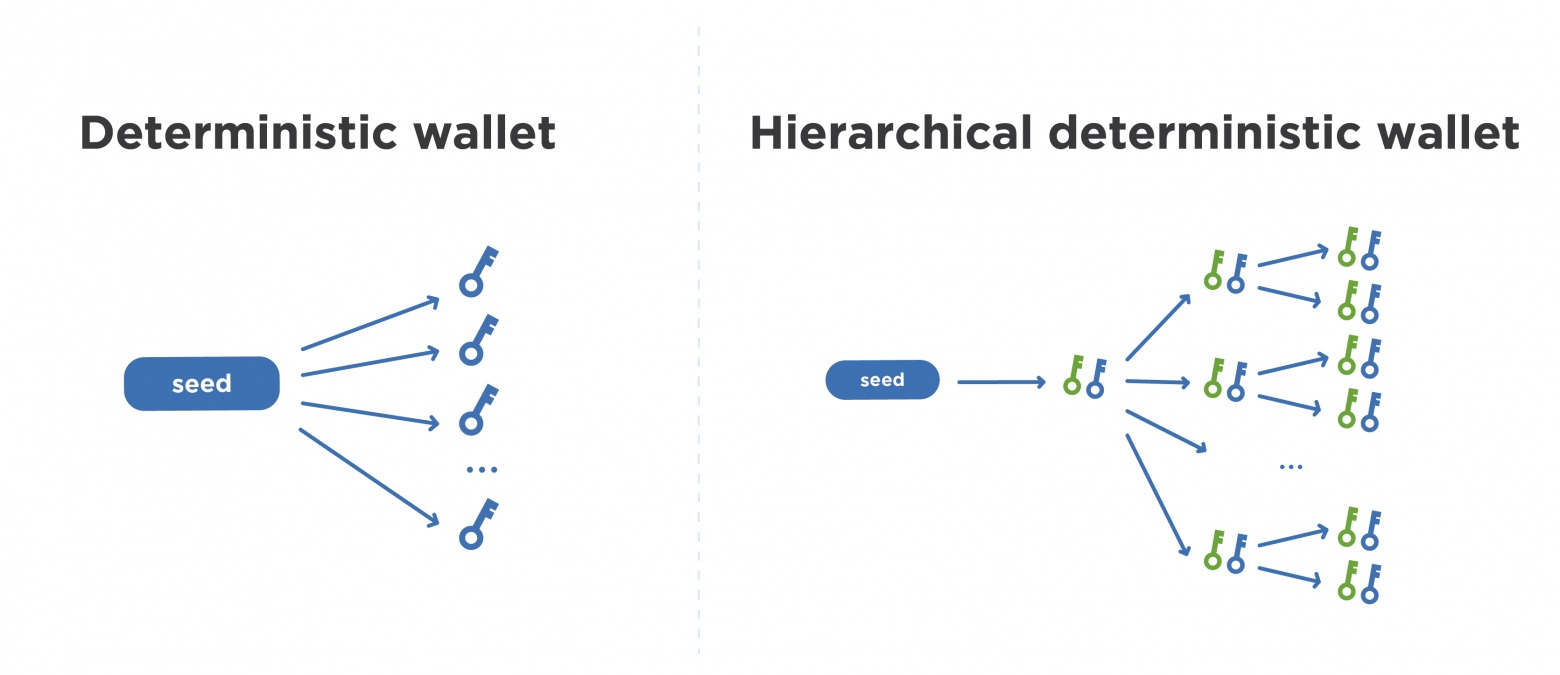
Обычный детерминистический кошелек имеет некоторый seed, из которого напрямую генерируется огромное множество личных ключей. Их количество может быть ограничено только размерностью индекса, который конкатенируется к секрету перед хешированием. Обычно это 4 байта, то есть пространство возможных вариантов допускает около 4 миллиардов уникальных ключей детерминистического кошелька. На практике этого должно хватить для любой ситуации.
Перейдем к иерархическому детерминистическому кошельку, схема разворачивания ключей которого представлена пока в упрощенном виде. Есть seed, из которого напрямую получается пара мастер-ключей. Если в обычном детерминистическом кошельке мы получаем личный ключ, то здесь мы получаем пару ключей. Более того, есть уровни иерархии, на каждом из которых мы рассчитываем индекс для порождения дочернего ключа. Мы также можем строить ветки открытых ключей и ветки личных ключей.
В отношении HD кошельков стоит отметить, что согласно правилам BIP32 на каждом уровне иерархии узел порождения имеет три объекта: личный ключ (private key), открытый ключ (public key) и код цепочки (chain code), который используется для порождения следующего уровня иерархии.
Рассмотрим более детально схему генерации ключей по BIP32.
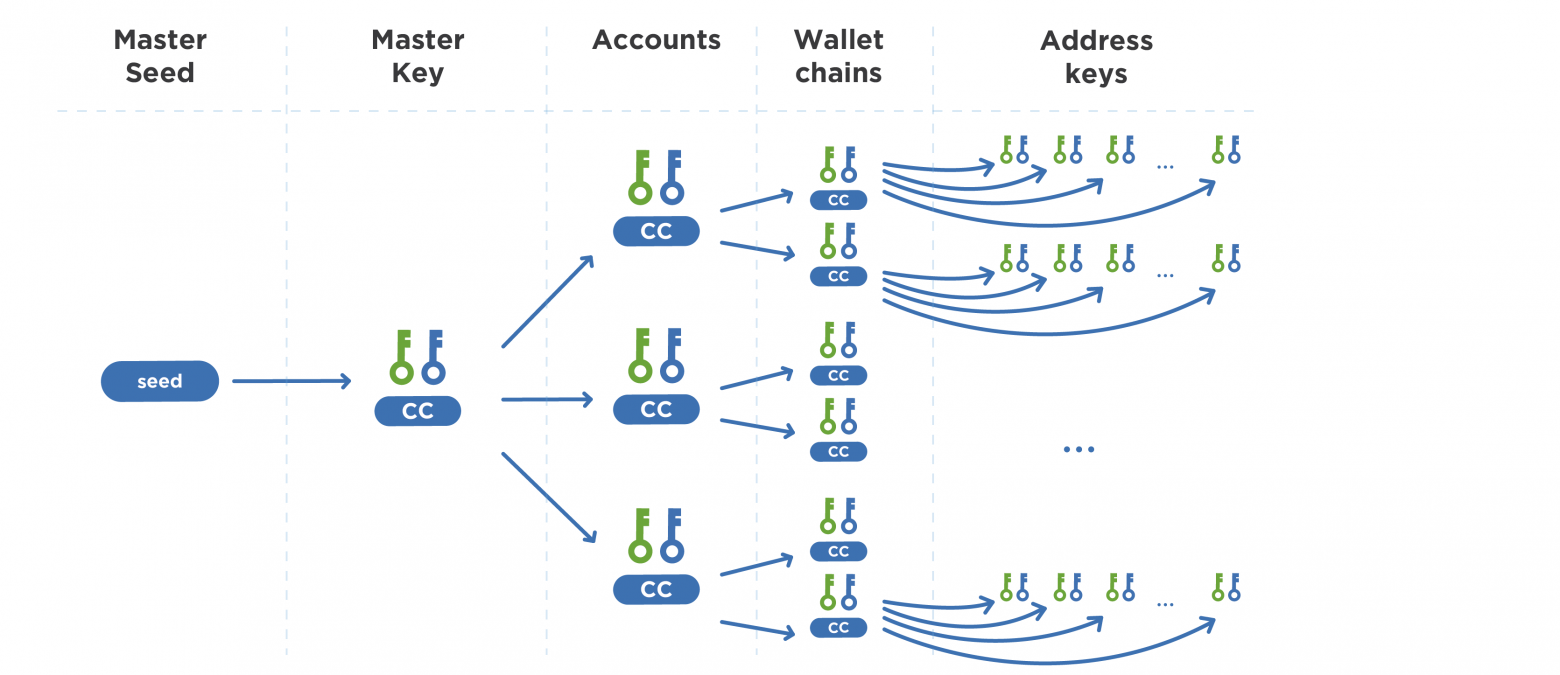
Все начинается с seed, его еще называют master seed, из которого рассчитывается нулевой уровень иерархии — пара master keys и chain code.
Из пары мастер-ключей может генерироваться огромное множество пар ключей с определенными индексами. Формируется новый уровень иерархии, который используется для генерации аккаунтов. Допустим, у одного пользователя есть seed и он хочет создать несколько адресов, которые будут отличаться друг от друга. Монеты этих адресов не будут смешиваться, не будут публиковаться вместе, а в готовых транзакциях между ними нельзя будет найти связь. Данные ключи будут использоваться полностью отдельно друг от друга. В одном из аккаунтов группа ключей будет использоваться для рабочего бюджета, в другом — для личного бюджета, а еще один аккаунт — для черной бухгалтерии. Монеты не будут смешиваться друг с другом.
Следующий уровень иерархии определяет разные цепочки генерирования ключей. Чаще всего используются цепочки с индексами 0 и 1. Цепочка с индексом 0 будет генерировать конечные ключи для формирования адреса для входящих платежей, а цепочка с индексом 1 будет генерировать кошельки, на которые будут приходить монеты, отправленные пользователем себе, то есть сдача. Это нужно, чтобы кошелек на программном уровне отличал отправленные извне платежи от сдачи, рассчитывал изменения баланса каждой транзакции и составлял наглядный список с историей всех платежей. Это упрощает разработку кошелька и его использование для повседневных платежей.
Теперь давайте перейдем к математической составляющей процессов иерархической генерации ключей. Начнем с того, что рассмотрим hash-based message authentication code. Это другой класс расчета хеш-функций. Отличается она тем, что принимает на вход два значения, а не одно. Первое значение — это секретный ключ, а второе — само сообщение.
K — ключ
m — сообщение
opad, ipad — некоторые константные значения, необходимые для формирования отличающихся друг от друга ключей на разных этапах хеширования.
В качестве хеш-функции используется SHA-512.
Особенность состоит в том, что для использования HMAC, нужно владеть секретным ключом, для того чтобы получить правильное хеш-значение сообщения.
Итак, для расчета хеш-значения по HMAC значение ключа XOR-ится с константным значением ipad, после чего результат хешируется. К этому значению конкатенируется сообщение, после чего рассчитывается XOR ключа с константным значением, конкатенируется с хеш-значением, после чего снова хешируется. В итоге мы получаем 512 бит хеш-значения.
Давайте рассмотрим несколько функций, которые используются при расчете иерархических ключей.

Первым делом нас интересует преобразование master seed в пару master key. После этого нужно получить из личного родительского ключа дочерний личный ключ и дочерний открытый ключ. Во втором случае используется точно такая же функция, как и в первом, но добавляется умножение числа на базовую точку, поэтому отдельно не будет рассматриваться. Далее следует получение из открытого родительского ключа дочернего открытого. Стоит отметить, что получение из родительского открытого ключа дочернего личного невозможно. Это ограничение обусловлено определенными свойствами, присущими HD кошелькам, которые мы рассмотрим дальше.
Итак, пройдемся по каждой из функций порождения отдельно.

Для получения мастер-ключа из мастер-сида используется функция HMAC, где в качестве ключа передается константная строка “Bitcoin seed”, а в качестве сообщения сами данные основного секрета. Таким образом, получается хеш-значение длиной 512 бит, которое мы рассматриваем как две части: левую и правую. Левая часть является master private key, а правая часть будет chain code. Дальше эти значения будут использоваться для порождения последующих уровней дочерних ключей.
Для того чтобы получить master public, достаточно умножить значение базовой точки на значение master private key. Как видим, это происходит по аналогии с обычными ключами в группе точек на эллиптической кривой.
Теперь посмотрим как происходит дочерний личный ключ из родительского личного.
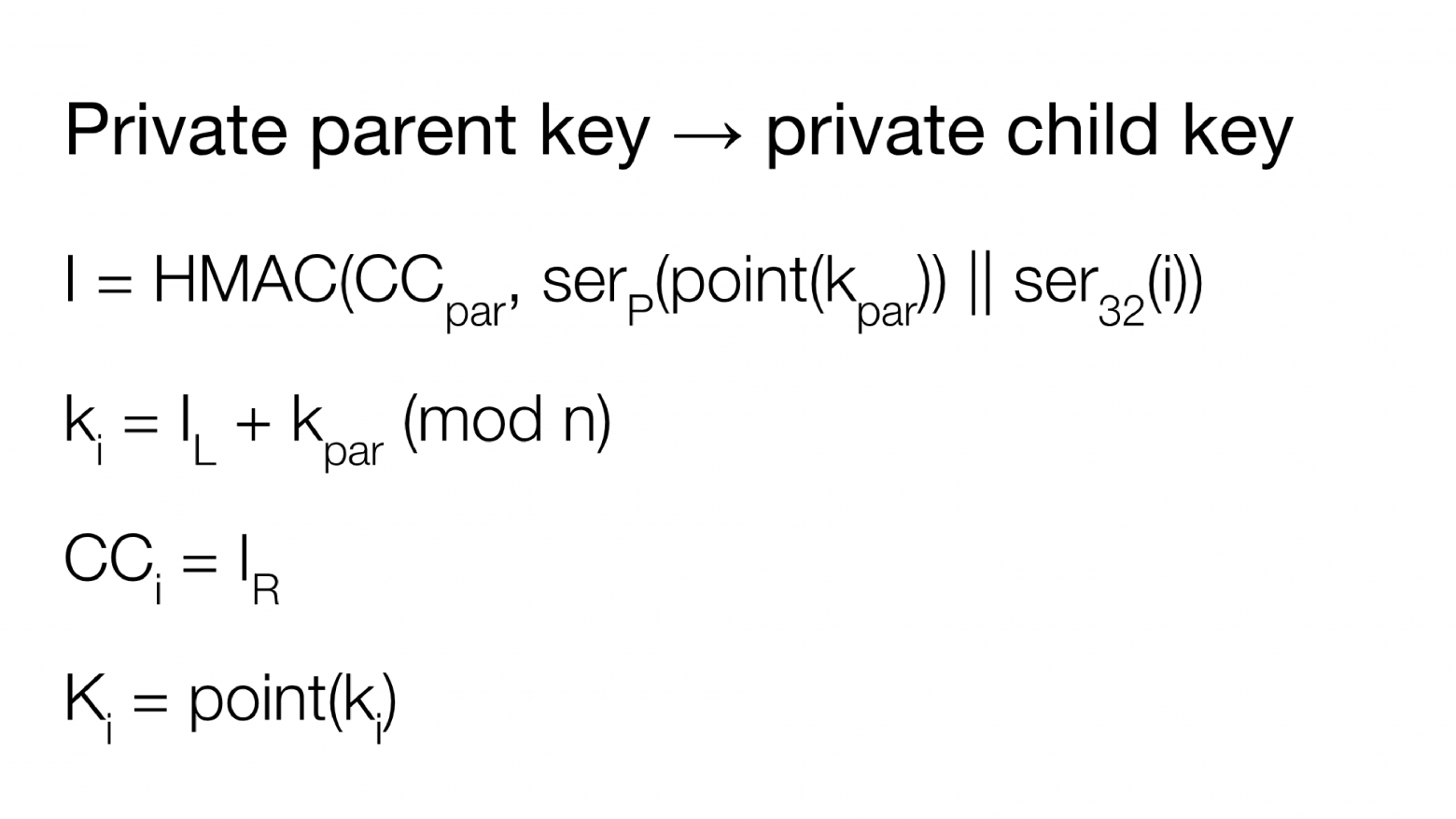
Снова воспользуемся функцией HMAC. В качестве ключа мы передаем chain code текущего уровня иерархии, а в качестве сообщения — конкатенацию, где первой частью будет личный родительский ключ, умноженный на базовую точку. Фактически это приведение к точке и сериализация этой точки. Конкатенация происходит с индексом дочернего ключа, который мы хотим получить, сериализованного в 32 бита, то есть в 4 байта.
По результату работы функции HMAC мы получаем значение I, и снова его рассматриваем по отдельности: левую и правую части выходных значений по 256 бит. Тогда дочерний личный ключ мы рассчитываем путем прибавления к левому выходному значению
мы рассчитываем путем прибавления к левому выходному значению  значения родительского личного ключа. Сложение выполняем по модулю n, где n — это порядок базовой точки эллиптической кривой, для того чтобы не превысить максимальное значение личного ключа. Таким образом, мы получили дочерний личный ключ.
значения родительского личного ключа. Сложение выполняем по модулю n, где n — это порядок базовой точки эллиптической кривой, для того чтобы не превысить максимальное значение личного ключа. Таким образом, мы получили дочерний личный ключ.
Соответственно, дочерний chain code будет равен правому выходному значению функции HMAC, то есть . Если мы хотим из личного родительского ключа найти дочерний открытый ключ, умножаем значение
. Если мы хотим из личного родительского ключа найти дочерний открытый ключ, умножаем значение  на значение базовой точки на эллиптической кривой. Так мы получим открытый ключ
на значение базовой точки на эллиптической кривой. Так мы получим открытый ключ  .
.
Как же нам рассчитать из открытого родительского ключа дочерний открытый ключ?

Здесь расчет будет немного иным. Мы передаем в качестве ключа chain code текущего уровня иерархии в функцию HMAC, после чего мы сериализируем родительский открытый ключ и конкатенируем его с нужным индексом, сериализованным в 32 бита. Входные данные получены точно таким же образом, как и в предыдущем случае. Для расчета открытого ключа мы берем левую часть выходного значения функции HMAC, и рассматриваем его, как 256 бит, взятых по модулю порядка базовой точки, приводим к точке на эллиптической кривой, то есть умножаем на базовую точку, после чего складываем результат с родительским открытым ключом. Результатом сложения будет тоже точка, и это будет открытый дочерний ключ. Chain code для данного ключа будет правая часть выходного значения функции HMAC.
Тут может возникнуть логический вопрос о том, как личный и открытый ключи, полученные разным образом, будут соответствовать друг другу. Действительно ли из порожденного публичным образом открытого ключа можно получить точно такое же значение, взяв личный ключ, полученный другим образом, и умножив его на базовую точку? Это легко проверить.

Если вспомнить, как мы рассчитывали личный дочерний ключ, и умножить его на базовую точку, то есть привести к функции point, а потом вспомнить расчет дочернего открытого ключа и сравнить эти расчеты, то мы увидим, что если рассматривать родительский открытого ключ как произведение личного родительского ключа на базовую точку, то мы увидим, что были произведены одни и те же расчеты, просто в разном порядке.
В одном случае мы сложили личные ключи и умножили на базовую точку, а во втором случае мы сначала умножили значения на базовую точку, а потом сложили их и получили результат. Основываясь на том, что операция сложения точек на эллиптической кривой является аддитивной, мы можем сказать, что эти два значения равны — мы получим один и тот же открытый ключ, рассчитанный двумя способами.
Ради интереса мы можем посмотреть на пример открытого ключа, который был получен для тестовых значений и расчетов BIP32. Если наша Entropy состояла из 128 бит, то в шестнадцатеричной системе счисления это будет выглядеть, как на изображении ниже.

Это же значение, закодированное в мнемоническую фразу по BIP39, будет выглядеть как показанные 12 слов. Если использовать эту мнемоническую фразу как мастер-сид для иерархической генерации ключей, то вы получите такой master private key с соответствующим chain code по 256 бит.
Есть еще такие понятия как расширенный открытый ключ и расширенный личный ключ. Как это используется? Чтобы лучше понять, опишем наглядную ситуацию.
Допустим, у нас есть определенный пользователь и некоторый сервис. Сервис с определенной частотой передает платежи, например в биткоинах, пользователю. И пользователь, и сервис заинтересованы в том, чтобы использовать для каждого платежа новый адрес, для того чтобы усложнить для внешнего наблюдателя установление факта и запутывание истории взаимодействия друг с другом.
В самом простом случае это выглядело бы так: пользователь для каждого входящего платежа формирует новую пару ключей, вычисляет адрес, который передает сервису, после чего сервис может сформировать транзакцию и выполнить платеж. Однако это неудобно ни для одной из сторон, если интенсивность этих платежей высокая.
В подобной ситуации от неудобств помогает избавиться расширенный открытый ключ (extended public key, xPubKey). Пользователь может дать возможность стороннему сервису вместо себя генерировать такие адреса, которые будут известны сервису, но личные ключи будут только у пользователя. Сервис может генерировать какое-угодно количество адресов без ведома пользователя и отправлять на них средства, а пользователь может, когда ему будет удобно, развернуть личные ключи и получить доступ к любому из этих адресов.
Как это работает? Пользователю нужно сгенерировать новый аккаунт на втором уровне иерархии ключей, рассчитать для него открытый ключ и chain code для текущего уровня. После этого нужно передать сервису и открытый ключ, и chain code. Для удобства было введено кодирование Base58Check Encoding, о котором мы говорили (здесь есть специальная версия). Далее, конкатенируется открытый ключ, chain code и контрольная сумма. Это все кодируется в систему счисления по основанию 58 и мы получаем уже закодированный по определенному стандарту открытый расширенный ключ. Он начинается с символов “xpub”, что легко распознается. Он будет выглядеть, как показано на изображении.

Сервис может принять такой ключ и развернуть по BIP32 открытые ключи для пользователя, из них получать адреса и платить на них. Однако соответствующие личные ключи может вычислить только пользователь.
В иерархическом порождении ключей есть такое понятие, как hardened derivation. Это такой подход, который не позволяет рассчитывать дочерние открытые ключи из соответствующего родительского открытого ключа. От нормального порождения это отличается тем, что в нем мы используем в качестве сообщения функции HMAC конкатенацию сериализованной точки как родительского открытого ключа, а в hardened derivation мы используем сериализацию родительского личного ключа.
Кроме того, отличается вычисление индекса. Индекс в нормальном порождении напрямую сериализуется в 32 бита, а в hardened derivation он несколько преобразуется: к нему добавляется константное значение , что устанавливает старший бит в 1 (становится легко отличать типы деривации). Соответственно, пространство вариантов возможных ключей одинаково как для нормального порождения, так и для hardened derivation и равно
, что устанавливает старший бит в 1 (становится легко отличать типы деривации). Соответственно, пространство вариантов возможных ключей одинаково как для нормального порождения, так и для hardened derivation и равно  .
.

Таким образом, имея родительский открытый ключ и hardened derivation, невозможно рассчитать дочерние открытые ключи. Если злоумышленник получит родительский открытый ключ, то он не сможет вычислить дочерние ключи. Следовательно, не сможет вычислить адреса и связь их с полученным родительским ключом. В случае normal derivation, то есть в обычном, такой функцией можно пользоваться и прослеживать взаимосвязь адресов между собой.
Давайте поговорим о путях, по которым могут порождаться ключи.

На каждом уровне иерархии есть определенный индекс, который определяет аспекты порождения ключей. Путь от Мастер-ключа до конечного ключа может записываться через слэши в виде индексов. Если речь идет о личном ключе то запись начинается с маленькой “m”, а если речь о порождении открытого ключа, то с большой “M”. Если индекс обозначен апострофом, то следует понимать, что речь идет о hardened derivation, без апострофа — normal derivation.
Рассмотрим один из популярных путей порождения ключей, который используется в BIP32, где и были определены иерархические ключи.

Он использует такой путь, где нулевым уровнем иерархии является мастер-ключ. Далее следуют индексы аккаунтов, которые обозначают одного и того же пользователя, после чего идут цепочки, где могут быть цепочки адресов, которые публикуются вовне для принятия входящих платежей, а с индексом 1 будут создаваться те цепочки, на которые сам пользователь отправляет себе платежи (чаще всего это сдача). Конечный индекс будет использоваться для порождения тех ключей, из которых будут рассчитываться адреса.
Для того чтобы по стандарту BIP32 рассчитать самый первый ключ с индексом 0, мы будем иметь m, 0 с порождением hardened, chain — 0, индекс — 0 (m/0’/0/0). Так мы получим путь для первого иерархически порожденного ключа.
Существует предложение по улучшению Биткоина, оно называется BIP43, которое предполагает запись в первый уровень иерархии номера улучшения, которое предлагает новый путь порождения (m/bip_number’/*).

Таким образом, появился BIP44, который использовал особенность предыдущего предложения, то есть для первого уровня иерархии записывается индекс 44, а предложил следующие улучшения: в индексе второго уровня иерархии записывать определенное значение, которое будет соответствовать типу монеты, которую мы используем для данного кошелька. Теперь в одном кошельке могут разворачиваться и использоваться ключи для разных валют.

Для Биткоина путь будет выглядеть, как “m/44’/0’/0’/0/0”, для Bitcoin testnet — “m/44’/1’/0’/0/0”, для Litecoin — “m/44’/2’/0’/0/0”, для Dash — “m/44’/5’/0’/0/0”. Интересно, что Ethereum использует точно такую же эллиптическую кривую для расчета ключей и электронно-цифровой подписи и для его кошелька путь будет выглядеть так “m/44’/60’/0’/0/0”.
Есть еще одно улучшение — BIP45. Улучшение нацелено на то, чтобы определить правила порождения ключей в случае их использования в multisignature кошельках и формирования адресов по BIP16, то есть P2SH. Он включает в себя предложение BIP43 и указывает на первом уровне иерархии индекс 45, на втором же уровне иерархии он требует указания подписанта (cosigner).
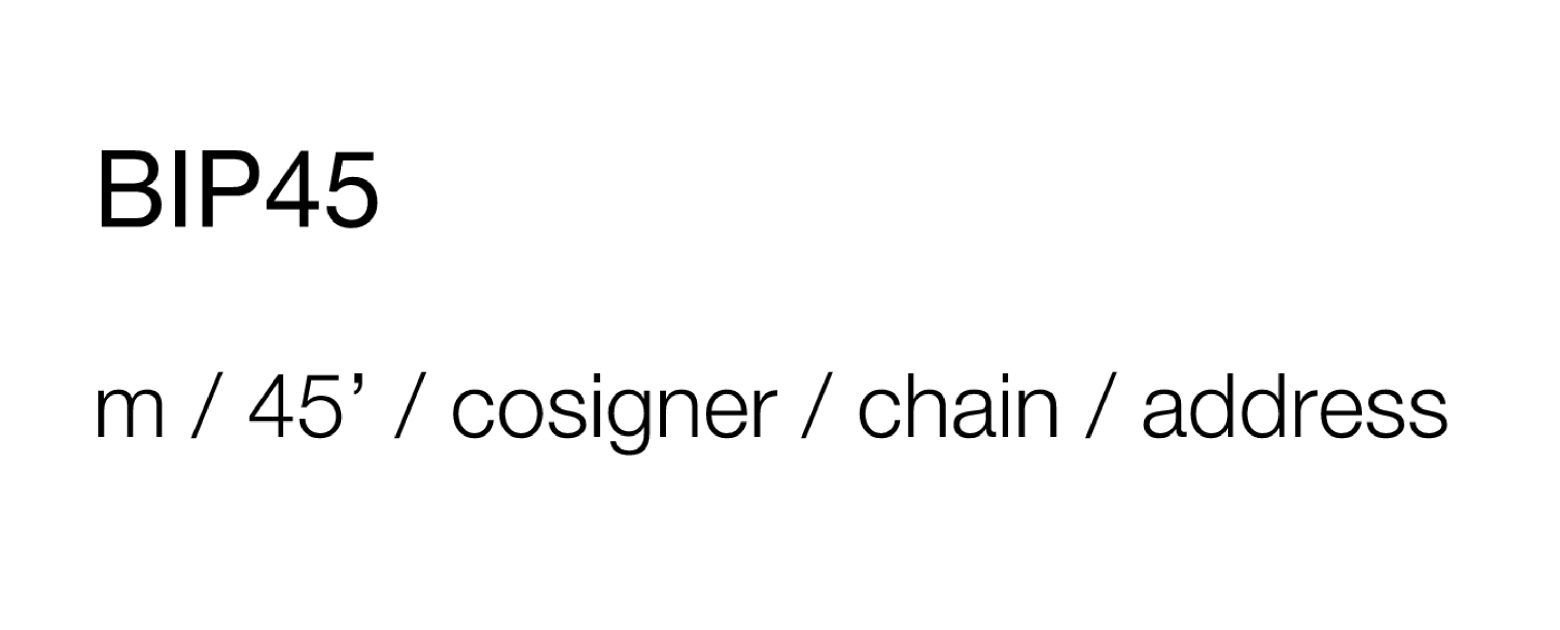
Например, есть правило мультиподписи 3-из-5. Следовательно есть 5 подписантов, но чтобы потратить монеты, нужно как минимум 3 подписи. Таким образом, каждый из подписантов будет иметь HD кошелек со своим мастер-сидом, а в своем пути будет указывать свой порядковый номер. Он может быть рассчитан, как индекс при сортировке ключей, порожденных на первом уровне иерархии каждого пользователя. Допустим, на первом уровне произошло порождение ключей у каждого пользователя, они обмениваются друг с другом, сортируют и узнают, у кого какой индекс для второго уровня иерархии. Это нужно, чтобы в дальнейшем исключить необходимость взаимодействовать подобным образом, а сразу правильно генерировать адреса и знать свой порядковый номер.
То есть можно единожды обменяться расширенным открытым ключом, чтобы потом самостоятельно, независимо от других участников группы, формировать multisignature адреса и принимать на них платежи.
Перейдем к часто задаваемым вопросам.
— Как отличаются master seeds в разных монетах?
Seed — это случайно сгенерированное число, какая-то последовательность бит, либо это мнемоническая фраза, сгенерированная, например, по BIP39, которая используется для порождения ключей. Она может быть использована как для одной монеты, так и для любой другой — не обязательно использовать разные мнемонические фразы для разных валют. Тем более, что есть BIP44, который определяет правила генерации ключей для разных валют из одной и той же мнемонической фразы. Эти личные ключи не будут пересекаться друг с другом, а будут использоваться для разных адресов разных валют.
— Словарь из BIP39, где 2048 слов для мнемонической фразы стандартизирован? Можно ли его использовать во всех кошельках и приложениях?
Дело в том, что этот стандарт описан для BIP39. Именно для BIP39 есть словари: английский, два японских, китайский, итальянский, русский, украинский и т. д. То есть если некоторое приложение заявляет, что оно использует BIP39 и дает возможность импортировать и экспортировать мнемоническую фразу, значит и набор слов оно использует тот же. Однако есть кошельки, которые используют не BIP39, а свою модификацию. Нужно смотреть описание кошелька и использовать либо стандартизированную, либо свою собственную разработку, либо разработку сервиса, который предлагает кошелек.
— На биржах и централизованных хранилищах типа Coinbase ключи кошельков всех пользователей генерируются из одной общей для всех сид-фразы или нет?
Сложно сказать, потому что они свою внутреннюю структуру не открывают, но те новые сервисы, которые появляются, могут либо отдельно генерировать ключи, либо использовать стандарт BIP32, либо использовать его модифицированную версию. Те сервисы, которые существовали еще до того, как появились стандарты по иерархической генерации ключей, скорее всего, продолжают генерировать просто отдельные личные ключи. Возможно, так ими проще управлять, если идет большой оборот всех ключей.
— Ключ — это точка на эллиптической кривой, то есть два очень больших числа X и Y?
Открытый ключ — да, это точка на эллиптической кривой, а личный ключ — это натуральное число, которое показывает, сколько раз саму с собой нужно сложить базовую точку. Сам открытый ключ состоит из двух значений — это координаты X и Y, каждая из которых имеет размер 256 бит.
— Что такое “приведение к точке” и сериализация точки и индекса?
Приведение к точке значит, что есть натуральное число, которое мы рассматриваем, как личный ключ. Базовую точку мы складываем саму с собой столько раз, то есть в группе точек на эллиптической кривой определена операция только сложения, то можно произвести умножение точки на натуральное число. Под сериализацией точки подразумевается запись определенным образом двух координат. Возможно, это сжатая запись, но не обязательно. Сжатая в смысле, что одну из координат, а именно Y преобразуют в знак, потом данные подставляются в уравнение и смотрят, где находится точка: выше или ниже. В случае сериализации индекса нужно понимать, что обычное число, которое, в зависимости от размера, можно записать в байтах или битах. Чем больше число, тем больший объем данных понадобится. В случае с теми вычислениями, которые мы рассмотрели, требуется число определенной длины. Нужно сериализовать его в определенную длину — 4 байта. В итоге, имеется в виду приведение индекса к 4-х байтовому числу. Если там остаются незаполненными старшие значения, значит они будут нулевыми.
— Кто придумал эти расчеты для derivation функций HD кошельков? Почему именно такие формулы, где есть обоснования и где можно подробнее об этом почитать?
Подробнее можно почитать именно в BIP32, если вас интересует мнемоническая фраза, то в BIP39, и т. д. Можно открыть GitHub, найти пользователя под ником Bitcoin. У него есть репозиторий Bitcoin, где хранится исходный код Биткоина, а есть репозиторий BIPs (первоисточник), где записаны все предложения по улучшению Биткоина.
Придумали делать расчеты именно так, потому что это завязано на группе точек эллиптической кривой. Когда хотели добиться такой функциональности, которая позволяет рассчитывать отдельно ветки открытых и личных ключей, при этом сохранить их соответствие друг другу, это был самый простой вариант реализации. Фактически разработчики использовали самый простой вариант, который позволяет добиться интересных свойств, используя ту криптографию, которая проверена временем. Авторов предложенных улучшений достаточно много. Сообщество Биткоина, участники которого предлагают какие-то разработки улучшений и математических преобразований, достаточно большое.
— Hardened derivation всегда только на втором уровне иерархии?
Все зависит от ситуации. В случае с порождением ключей для мультиподписи имеет смысл делать hardened derivation только на первом уровне иерархии. В BIP44 hardened derivation применяется к первым трем уровням: на первом уровне находится номер самого BIP, на втором — номер аккаунта, где это актуально, на третьем — номер валюты, где это тоже имеет смысл. Допустим, вам вряд ли понравится, если вы выложите открытый ключ, а через него люди смогут отследить все ваши адреса в Биткоине. Если вы используете аккаунт для получения платежей от определенных сервисов, тогда вы можете разглашать этот ключ и hardened derivation вам здесь не нужен.
— Где возможно применить иерархическую генерацию ключей?
Можно применить при работе с биржей, чтобы биржа все время вам платила на разные адреса. Хотя в данном случае лучше уж вручную все это организовать. Наиболее актуально это для цифровых кошельков повседневного использования, потому что здесь очень простой процесс создания резервной копии личных ключей и восстановления кошелька. Также поддерживается генерация ключей для разных валют, а сам стандарт уже используется в разных реализациях цифровых кошельков. Ключи между такими кошельками удобно переносить, используя одну и ту же мнемоническую фразу.
Данной теме посвящена одна из лекций онлайн-курса по Blockchain “Иерархическая генерация ключей”.
Deterministic wallet
В первую очередь давайте определим, что такое детерминистический кошелек (deterministic wallet). Когда мы говорим о генерации ключей, мы часто употребляем слово “кошелек”, потому что в контексте криптовалют владение личным ключом является доказательством владения монетами, а в данном случае кошелек и ключ имеют похожий смысл.
Deterministic wallet — это кошелек, в котором все используемые личные ключи были порождены из одного общего для всех ключей секрета. Особенность состоит в том, что есть возможность из одного секрета породить сколько-угодно пар ключей для электронной подписи. Можно использовать новые адреса для каждого входящего платежа и сдачи.
Удобно, что ключи такого кошелька можно легко перенести на другое устройство, сделать резервную копию и потом восстановить, потому что фактически нужно резервировать только один основной секрет. Кроме того, все порожденные из основного секрета личные ключи, друг с другом никак не связаны. Нельзя проследить и связь между порожденными адресами (определить что все они принадлежат одному пользователю), а имея порожденный личный ключ, нельзя восстановить общий секрет.
Кодирование основного секрета
Теперь поговорим о кодировании основного секрета. Здесь имеется некоторый стандартизированный подход, который был определен в BIP39. Это так называемое Check Encoding кодирование основного секрета в мнемоническую фразу — набор слов, который легко записать на бумагу и при необходимости запомнить. При вводе есть возможность проверить контрольную сумму, то есть выявить ошибку, если такая имеется, с довольно большой вероятностью.
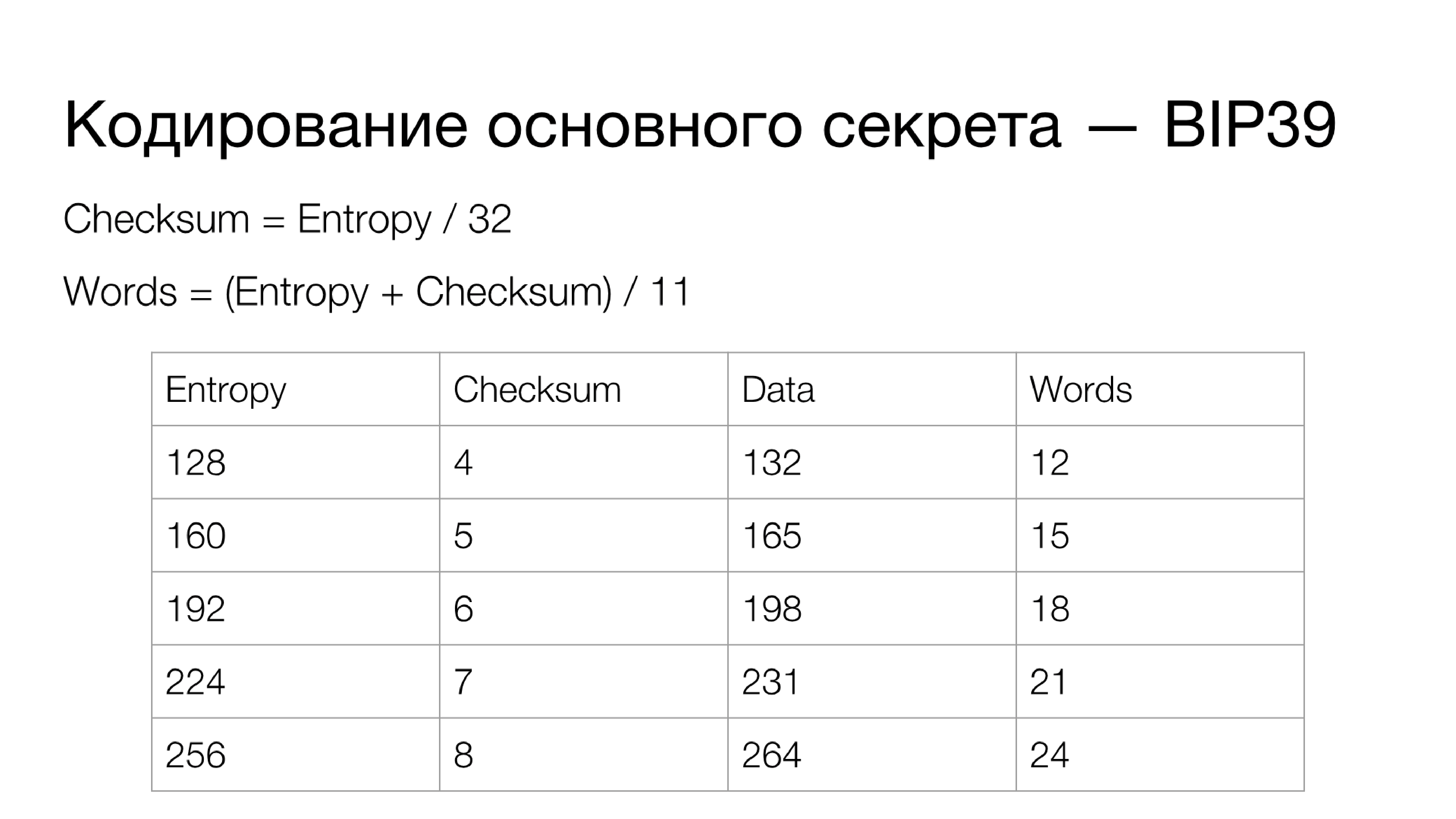
Как это работает? Фактически у вас есть основной секрет (Entropy) — данные, из которых разворачиваются все личные ключи кошелька. Этот секрет может иметь разную длину. Что касается контрольной суммы: на каждые 32 бита Entropy приходится 1 бит контрольной суммы, то есть Checksum по формуле рассчитывается, как длина Entropy в битах, разделенная на 32.
Entropy конкатенируется с контрольной суммой, которая рассчитывается, как двойной хеш SHA-256 (SHA-2 на длине 256 бит), после чего отрезается необходимое количество битов. Конкатенированные данные переводятся в другую систему счисления: из двоичной в систему счисления по основанию 2048 (как видим, 2048 — это
Фактически данные “нарезаются” частями по 11 бит. Есть словарь, состоящий из 2048 слов (
Первые четыре символа однозначно определяют слово в словаре, а остальные символы используются, чтобы завершить это слово до удобной формы для чтения, запоминания и т. д. Таким образом каждый фрагмент данных, состоящий из 11-ти бит, получает однозначное соответствие в виде слова из словаря. Если Entropy вашего секрета составляет 256 бит, то данные для кодирования составят 264 бита, а ваша мнемоническая фраза будет содержать 24 слова. Это основной подход к кодированию секрета кошельков в BIP39, который применяется на практике чаще всего.
Для того чтобы в будущем делать резервную копию и использовать ее, вам предлагается выписать эту фразу на внешний носитель. Лучше всего подойдет бумага, которую вы будете хранить в надежном месте. Так вы можете восстановить полный доступ ко всем своим ключам.
Типы детерминистических кошельков
Детерминистические кошельки бывают двух типов. Рассмотрим основные их отличия.
Первый из них самый простой. Основной секрет здесь конкатенируется с индексом дочернего ключа, который мы хотим получить, после чего конкатенированные данные хешируются. Чаще всего это происходит с помощью хеш-функции SHA-256.
Ко второму типу относятся иерархические детерминистические кошельки (hierarchical deterministic wallets, HD wallets), принципы которых определены в BIP32, и являются очень распространенным подходом к иерархической генерации ключей.
Deterministic generation
Рассмотрим отличия этих типов кошельков на схеме.

Обычный детерминистический кошелек имеет некоторый seed, из которого напрямую генерируется огромное множество личных ключей. Их количество может быть ограничено только размерностью индекса, который конкатенируется к секрету перед хешированием. Обычно это 4 байта, то есть пространство возможных вариантов допускает около 4 миллиардов уникальных ключей детерминистического кошелька. На практике этого должно хватить для любой ситуации.
Hierarchical deterministic generation
Перейдем к иерархическому детерминистическому кошельку, схема разворачивания ключей которого представлена пока в упрощенном виде. Есть seed, из которого напрямую получается пара мастер-ключей. Если в обычном детерминистическом кошельке мы получаем личный ключ, то здесь мы получаем пару ключей. Более того, есть уровни иерархии, на каждом из которых мы рассчитываем индекс для порождения дочернего ключа. Мы также можем строить ветки открытых ключей и ветки личных ключей.
Уровни иерархии
В отношении HD кошельков стоит отметить, что согласно правилам BIP32 на каждом уровне иерархии узел порождения имеет три объекта: личный ключ (private key), открытый ключ (public key) и код цепочки (chain code), который используется для порождения следующего уровня иерархии.
Схема иерархической генерации
Рассмотрим более детально схему генерации ключей по BIP32.

Все начинается с seed, его еще называют master seed, из которого рассчитывается нулевой уровень иерархии — пара master keys и chain code.
Из пары мастер-ключей может генерироваться огромное множество пар ключей с определенными индексами. Формируется новый уровень иерархии, который используется для генерации аккаунтов. Допустим, у одного пользователя есть seed и он хочет создать несколько адресов, которые будут отличаться друг от друга. Монеты этих адресов не будут смешиваться, не будут публиковаться вместе, а в готовых транзакциях между ними нельзя будет найти связь. Данные ключи будут использоваться полностью отдельно друг от друга. В одном из аккаунтов группа ключей будет использоваться для рабочего бюджета, в другом — для личного бюджета, а еще один аккаунт — для черной бухгалтерии. Монеты не будут смешиваться друг с другом.
Следующий уровень иерархии определяет разные цепочки генерирования ключей. Чаще всего используются цепочки с индексами 0 и 1. Цепочка с индексом 0 будет генерировать конечные ключи для формирования адреса для входящих платежей, а цепочка с индексом 1 будет генерировать кошельки, на которые будут приходить монеты, отправленные пользователем себе, то есть сдача. Это нужно, чтобы кошелек на программном уровне отличал отправленные извне платежи от сдачи, рассчитывал изменения баланса каждой транзакции и составлял наглядный список с историей всех платежей. Это упрощает разработку кошелька и его использование для повседневных платежей.
Hash-based message authentication code
Теперь давайте перейдем к математической составляющей процессов иерархической генерации ключей. Начнем с того, что рассмотрим hash-based message authentication code. Это другой класс расчета хеш-функций. Отличается она тем, что принимает на вход два значения, а не одно. Первое значение — это секретный ключ, а второе — само сообщение.
K — ключ
m — сообщение
opad, ipad — некоторые константные значения, необходимые для формирования отличающихся друг от друга ключей на разных этапах хеширования.
В качестве хеш-функции используется SHA-512.
Особенность состоит в том, что для использования HMAC, нужно владеть секретным ключом, для того чтобы получить правильное хеш-значение сообщения.
Итак, для расчета хеш-значения по HMAC значение ключа XOR-ится с константным значением ipad, после чего результат хешируется. К этому значению конкатенируется сообщение, после чего рассчитывается XOR ключа с константным значением, конкатенируется с хеш-значением, после чего снова хешируется. В итоге мы получаем 512 бит хеш-значения.
Функции деривации
Давайте рассмотрим несколько функций, которые используются при расчете иерархических ключей.

Первым делом нас интересует преобразование master seed в пару master key. После этого нужно получить из личного родительского ключа дочерний личный ключ и дочерний открытый ключ. Во втором случае используется точно такая же функция, как и в первом, но добавляется умножение числа на базовую точку, поэтому отдельно не будет рассматриваться. Далее следует получение из открытого родительского ключа дочернего открытого. Стоит отметить, что получение из родительского открытого ключа дочернего личного невозможно. Это ограничение обусловлено определенными свойствами, присущими HD кошелькам, которые мы рассмотрим дальше.
Итак, пройдемся по каждой из функций порождения отдельно.

Для получения мастер-ключа из мастер-сида используется функция HMAC, где в качестве ключа передается константная строка “Bitcoin seed”, а в качестве сообщения сами данные основного секрета. Таким образом, получается хеш-значение длиной 512 бит, которое мы рассматриваем как две части: левую и правую. Левая часть является master private key, а правая часть будет chain code. Дальше эти значения будут использоваться для порождения последующих уровней дочерних ключей.
Для того чтобы получить master public, достаточно умножить значение базовой точки на значение master private key. Как видим, это происходит по аналогии с обычными ключами в группе точек на эллиптической кривой.
Теперь посмотрим как происходит дочерний личный ключ из родительского личного.

Снова воспользуемся функцией HMAC. В качестве ключа мы передаем chain code текущего уровня иерархии, а в качестве сообщения — конкатенацию, где первой частью будет личный родительский ключ, умноженный на базовую точку. Фактически это приведение к точке и сериализация этой точки. Конкатенация происходит с индексом дочернего ключа, который мы хотим получить, сериализованного в 32 бита, то есть в 4 байта.
По результату работы функции HMAC мы получаем значение I, и снова его рассматриваем по отдельности: левую и правую части выходных значений по 256 бит. Тогда дочерний личный ключ
Соответственно, дочерний chain code будет равен правому выходному значению функции HMAC, то есть
Как же нам рассчитать из открытого родительского ключа дочерний открытый ключ?

Здесь расчет будет немного иным. Мы передаем в качестве ключа chain code текущего уровня иерархии в функцию HMAC, после чего мы сериализируем родительский открытый ключ и конкатенируем его с нужным индексом, сериализованным в 32 бита. Входные данные получены точно таким же образом, как и в предыдущем случае. Для расчета открытого ключа мы берем левую часть выходного значения функции HMAC, и рассматриваем его, как 256 бит, взятых по модулю порядка базовой точки, приводим к точке на эллиптической кривой, то есть умножаем на базовую точку, после чего складываем результат с родительским открытым ключом. Результатом сложения будет тоже точка, и это будет открытый дочерний ключ. Chain code для данного ключа будет правая часть выходного значения функции HMAC.
Соответствие ключей друг другу
Тут может возникнуть логический вопрос о том, как личный и открытый ключи, полученные разным образом, будут соответствовать друг другу. Действительно ли из порожденного публичным образом открытого ключа можно получить точно такое же значение, взяв личный ключ, полученный другим образом, и умножив его на базовую точку? Это легко проверить.

Если вспомнить, как мы рассчитывали личный дочерний ключ, и умножить его на базовую точку, то есть привести к функции point, а потом вспомнить расчет дочернего открытого ключа и сравнить эти расчеты, то мы увидим, что если рассматривать родительский открытого ключ как произведение личного родительского ключа на базовую точку, то мы увидим, что были произведены одни и те же расчеты, просто в разном порядке.
В одном случае мы сложили личные ключи и умножили на базовую точку, а во втором случае мы сначала умножили значения на базовую точку, а потом сложили их и получили результат. Основываясь на том, что операция сложения точек на эллиптической кривой является аддитивной, мы можем сказать, что эти два значения равны — мы получим один и тот же открытый ключ, рассчитанный двумя способами.
Пример открытого ключа
Ради интереса мы можем посмотреть на пример открытого ключа, который был получен для тестовых значений и расчетов BIP32. Если наша Entropy состояла из 128 бит, то в шестнадцатеричной системе счисления это будет выглядеть, как на изображении ниже.

Это же значение, закодированное в мнемоническую фразу по BIP39, будет выглядеть как показанные 12 слов. Если использовать эту мнемоническую фразу как мастер-сид для иерархической генерации ключей, то вы получите такой master private key с соответствующим chain code по 256 бит.
Расширенные ключи
Есть еще такие понятия как расширенный открытый ключ и расширенный личный ключ. Как это используется? Чтобы лучше понять, опишем наглядную ситуацию.
Допустим, у нас есть определенный пользователь и некоторый сервис. Сервис с определенной частотой передает платежи, например в биткоинах, пользователю. И пользователь, и сервис заинтересованы в том, чтобы использовать для каждого платежа новый адрес, для того чтобы усложнить для внешнего наблюдателя установление факта и запутывание истории взаимодействия друг с другом.
В самом простом случае это выглядело бы так: пользователь для каждого входящего платежа формирует новую пару ключей, вычисляет адрес, который передает сервису, после чего сервис может сформировать транзакцию и выполнить платеж. Однако это неудобно ни для одной из сторон, если интенсивность этих платежей высокая.
Расширенный открытый ключ
В подобной ситуации от неудобств помогает избавиться расширенный открытый ключ (extended public key, xPubKey). Пользователь может дать возможность стороннему сервису вместо себя генерировать такие адреса, которые будут известны сервису, но личные ключи будут только у пользователя. Сервис может генерировать какое-угодно количество адресов без ведома пользователя и отправлять на них средства, а пользователь может, когда ему будет удобно, развернуть личные ключи и получить доступ к любому из этих адресов.
Как это работает? Пользователю нужно сгенерировать новый аккаунт на втором уровне иерархии ключей, рассчитать для него открытый ключ и chain code для текущего уровня. После этого нужно передать сервису и открытый ключ, и chain code. Для удобства было введено кодирование Base58Check Encoding, о котором мы говорили (здесь есть специальная версия). Далее, конкатенируется открытый ключ, chain code и контрольная сумма. Это все кодируется в систему счисления по основанию 58 и мы получаем уже закодированный по определенному стандарту открытый расширенный ключ. Он начинается с символов “xpub”, что легко распознается. Он будет выглядеть, как показано на изображении.

Сервис может принять такой ключ и развернуть по BIP32 открытые ключи для пользователя, из них получать адреса и платить на них. Однако соответствующие личные ключи может вычислить только пользователь.
Hardened derivation
В иерархическом порождении ключей есть такое понятие, как hardened derivation. Это такой подход, который не позволяет рассчитывать дочерние открытые ключи из соответствующего родительского открытого ключа. От нормального порождения это отличается тем, что в нем мы используем в качестве сообщения функции HMAC конкатенацию сериализованной точки как родительского открытого ключа, а в hardened derivation мы используем сериализацию родительского личного ключа.
Кроме того, отличается вычисление индекса. Индекс в нормальном порождении напрямую сериализуется в 32 бита, а в hardened derivation он несколько преобразуется: к нему добавляется константное значение

Таким образом, имея родительский открытый ключ и hardened derivation, невозможно рассчитать дочерние открытые ключи. Если злоумышленник получит родительский открытый ключ, то он не сможет вычислить дочерние ключи. Следовательно, не сможет вычислить адреса и связь их с полученным родительским ключом. В случае normal derivation, то есть в обычном, такой функцией можно пользоваться и прослеживать взаимосвязь адресов между собой.
Пути порождения
Давайте поговорим о путях, по которым могут порождаться ключи.

На каждом уровне иерархии есть определенный индекс, который определяет аспекты порождения ключей. Путь от Мастер-ключа до конечного ключа может записываться через слэши в виде индексов. Если речь идет о личном ключе то запись начинается с маленькой “m”, а если речь о порождении открытого ключа, то с большой “M”. Если индекс обозначен апострофом, то следует понимать, что речь идет о hardened derivation, без апострофа — normal derivation.
Рассмотрим один из популярных путей порождения ключей, который используется в BIP32, где и были определены иерархические ключи.

Он использует такой путь, где нулевым уровнем иерархии является мастер-ключ. Далее следуют индексы аккаунтов, которые обозначают одного и того же пользователя, после чего идут цепочки, где могут быть цепочки адресов, которые публикуются вовне для принятия входящих платежей, а с индексом 1 будут создаваться те цепочки, на которые сам пользователь отправляет себе платежи (чаще всего это сдача). Конечный индекс будет использоваться для порождения тех ключей, из которых будут рассчитываться адреса.
Для того чтобы по стандарту BIP32 рассчитать самый первый ключ с индексом 0, мы будем иметь m, 0 с порождением hardened, chain — 0, индекс — 0 (m/0’/0/0). Так мы получим путь для первого иерархически порожденного ключа.
Существует предложение по улучшению Биткоина, оно называется BIP43, которое предполагает запись в первый уровень иерархии номера улучшения, которое предлагает новый путь порождения (m/bip_number’/*).

Таким образом, появился BIP44, который использовал особенность предыдущего предложения, то есть для первого уровня иерархии записывается индекс 44, а предложил следующие улучшения: в индексе второго уровня иерархии записывать определенное значение, которое будет соответствовать типу монеты, которую мы используем для данного кошелька. Теперь в одном кошельке могут разворачиваться и использоваться ключи для разных валют.

Для Биткоина путь будет выглядеть, как “m/44’/0’/0’/0/0”, для Bitcoin testnet — “m/44’/1’/0’/0/0”, для Litecoin — “m/44’/2’/0’/0/0”, для Dash — “m/44’/5’/0’/0/0”. Интересно, что Ethereum использует точно такую же эллиптическую кривую для расчета ключей и электронно-цифровой подписи и для его кошелька путь будет выглядеть так “m/44’/60’/0’/0/0”.
Есть еще одно улучшение — BIP45. Улучшение нацелено на то, чтобы определить правила порождения ключей в случае их использования в multisignature кошельках и формирования адресов по BIP16, то есть P2SH. Он включает в себя предложение BIP43 и указывает на первом уровне иерархии индекс 45, на втором же уровне иерархии он требует указания подписанта (cosigner).

Например, есть правило мультиподписи 3-из-5. Следовательно есть 5 подписантов, но чтобы потратить монеты, нужно как минимум 3 подписи. Таким образом, каждый из подписантов будет иметь HD кошелек со своим мастер-сидом, а в своем пути будет указывать свой порядковый номер. Он может быть рассчитан, как индекс при сортировке ключей, порожденных на первом уровне иерархии каждого пользователя. Допустим, на первом уровне произошло порождение ключей у каждого пользователя, они обмениваются друг с другом, сортируют и узнают, у кого какой индекс для второго уровня иерархии. Это нужно, чтобы в дальнейшем исключить необходимость взаимодействовать подобным образом, а сразу правильно генерировать адреса и знать свой порядковый номер.
То есть можно единожды обменяться расширенным открытым ключом, чтобы потом самостоятельно, независимо от других участников группы, формировать multisignature адреса и принимать на них платежи.
Вопросы
Перейдем к часто задаваемым вопросам.
— Как отличаются master seeds в разных монетах?
Seed — это случайно сгенерированное число, какая-то последовательность бит, либо это мнемоническая фраза, сгенерированная, например, по BIP39, которая используется для порождения ключей. Она может быть использована как для одной монеты, так и для любой другой — не обязательно использовать разные мнемонические фразы для разных валют. Тем более, что есть BIP44, который определяет правила генерации ключей для разных валют из одной и той же мнемонической фразы. Эти личные ключи не будут пересекаться друг с другом, а будут использоваться для разных адресов разных валют.
— Словарь из BIP39, где 2048 слов для мнемонической фразы стандартизирован? Можно ли его использовать во всех кошельках и приложениях?
Дело в том, что этот стандарт описан для BIP39. Именно для BIP39 есть словари: английский, два японских, китайский, итальянский, русский, украинский и т. д. То есть если некоторое приложение заявляет, что оно использует BIP39 и дает возможность импортировать и экспортировать мнемоническую фразу, значит и набор слов оно использует тот же. Однако есть кошельки, которые используют не BIP39, а свою модификацию. Нужно смотреть описание кошелька и использовать либо стандартизированную, либо свою собственную разработку, либо разработку сервиса, который предлагает кошелек.
— На биржах и централизованных хранилищах типа Coinbase ключи кошельков всех пользователей генерируются из одной общей для всех сид-фразы или нет?
Сложно сказать, потому что они свою внутреннюю структуру не открывают, но те новые сервисы, которые появляются, могут либо отдельно генерировать ключи, либо использовать стандарт BIP32, либо использовать его модифицированную версию. Те сервисы, которые существовали еще до того, как появились стандарты по иерархической генерации ключей, скорее всего, продолжают генерировать просто отдельные личные ключи. Возможно, так ими проще управлять, если идет большой оборот всех ключей.
— Ключ — это точка на эллиптической кривой, то есть два очень больших числа X и Y?
Открытый ключ — да, это точка на эллиптической кривой, а личный ключ — это натуральное число, которое показывает, сколько раз саму с собой нужно сложить базовую точку. Сам открытый ключ состоит из двух значений — это координаты X и Y, каждая из которых имеет размер 256 бит.
— Что такое “приведение к точке” и сериализация точки и индекса?
Приведение к точке значит, что есть натуральное число, которое мы рассматриваем, как личный ключ. Базовую точку мы складываем саму с собой столько раз, то есть в группе точек на эллиптической кривой определена операция только сложения, то можно произвести умножение точки на натуральное число. Под сериализацией точки подразумевается запись определенным образом двух координат. Возможно, это сжатая запись, но не обязательно. Сжатая в смысле, что одну из координат, а именно Y преобразуют в знак, потом данные подставляются в уравнение и смотрят, где находится точка: выше или ниже. В случае сериализации индекса нужно понимать, что обычное число, которое, в зависимости от размера, можно записать в байтах или битах. Чем больше число, тем больший объем данных понадобится. В случае с теми вычислениями, которые мы рассмотрели, требуется число определенной длины. Нужно сериализовать его в определенную длину — 4 байта. В итоге, имеется в виду приведение индекса к 4-х байтовому числу. Если там остаются незаполненными старшие значения, значит они будут нулевыми.
— Кто придумал эти расчеты для derivation функций HD кошельков? Почему именно такие формулы, где есть обоснования и где можно подробнее об этом почитать?
Подробнее можно почитать именно в BIP32, если вас интересует мнемоническая фраза, то в BIP39, и т. д. Можно открыть GitHub, найти пользователя под ником Bitcoin. У него есть репозиторий Bitcoin, где хранится исходный код Биткоина, а есть репозиторий BIPs (первоисточник), где записаны все предложения по улучшению Биткоина.
Придумали делать расчеты именно так, потому что это завязано на группе точек эллиптической кривой. Когда хотели добиться такой функциональности, которая позволяет рассчитывать отдельно ветки открытых и личных ключей, при этом сохранить их соответствие друг другу, это был самый простой вариант реализации. Фактически разработчики использовали самый простой вариант, который позволяет добиться интересных свойств, используя ту криптографию, которая проверена временем. Авторов предложенных улучшений достаточно много. Сообщество Биткоина, участники которого предлагают какие-то разработки улучшений и математических преобразований, достаточно большое.
— Hardened derivation всегда только на втором уровне иерархии?
Все зависит от ситуации. В случае с порождением ключей для мультиподписи имеет смысл делать hardened derivation только на первом уровне иерархии. В BIP44 hardened derivation применяется к первым трем уровням: на первом уровне находится номер самого BIP, на втором — номер аккаунта, где это актуально, на третьем — номер валюты, где это тоже имеет смысл. Допустим, вам вряд ли понравится, если вы выложите открытый ключ, а через него люди смогут отследить все ваши адреса в Биткоине. Если вы используете аккаунт для получения платежей от определенных сервисов, тогда вы можете разглашать этот ключ и hardened derivation вам здесь не нужен.
— Где возможно применить иерархическую генерацию ключей?
Можно применить при работе с биржей, чтобы биржа все время вам платила на разные адреса. Хотя в данном случае лучше уж вручную все это организовать. Наиболее актуально это для цифровых кошельков повседневного использования, потому что здесь очень простой процесс создания резервной копии личных ключей и восстановления кошелька. Также поддерживается генерация ключей для разных валют, а сам стандарт уже используется в разных реализациях цифровых кошельков. Ключи между такими кошельками удобно переносить, используя одну и ту же мнемоническую фразу.
Данной теме посвящена одна из лекций онлайн-курса по Blockchain “Иерархическая генерация ключей”.