boygenius Jan 21 2022 at 14:02

CatBoost, XGBoost и выразительная способность решающих деревьев

42 min

50K

Open Data Science corporate blogProgramming*Mathematics*Machine learning*Artificial Intelligence

Сейчас существенная часть машинного обучения основана на решающих деревьях и их ансамблях, таких как CatBoost и XGBoost, но при этом не все имеют представление о том, как устроены эти алгоритмы "изнутри".

Данный обзор охватывает сразу несколько тем. Мы начнем с устройства решающего дерева и градиентного бустинга, затем подробно поговорим об XGBoost и CatBoost. Среди основных особенностей алгоритма CatBoost:

Упорядоченное target-кодирование категориальных признаков с большим числом значений (параметр one_hot_max_size)
Использование решающих таблиц (параметр по умолчанию grow_policy='SymmetricTree')
Разделение ветвей не только по отдельным признакам, но и по их комбинациям (параметр max_ctr_complexity)
Упорядоченный бустинг (параметр boosting_type='Ordered') для датасетов небольшого размера
Возможность работы с текстовыми признаками (параметр text_features метода fit) с помощью bag-of-words
Возможность обучения на GPU (параметр task_type='GPU' в методе fit), хотя это может сказаться на качестве

В конце обзора поговорим о методах интерпретации решающих деревьев (MDI, SHAP) и о выразительной способности решающих деревьев. Удивительно, но ансамбли деревьев ограниченной глубины, в том числе CatBoost, не являются универсальными аппроксиматорами: в данном обзоре приведено собственное исследование этого вопроса с доказательством (и экспериментальным подтверждением) того, что ансамбль деревьев глубины N не способен сколь угодно точно аппроксимировать функцию $y = x_1 x_2 \dots x_{N+1}$ . Поговорим также о выводах, которые можно из этого сделать.

Содержание

Структура решающих деревьев

Решающие деревья применяются в основном в задачах классификации и регрессии в машинном обучении на табличных данных (хотя могут быть и другие применения). В общем виде решающее дерево - это иерархическая схема принятия решений в виде графа. В промежуточных вершинах (звеньях) проверяются некие условия, и в зависимости от результатов выбирается путь в графе, который приводит к одной из конечных вершин (листьев).

В общем случае звенья и листья могут быть сложными функциями. Однако в большинстве практических реализаций каждый лист соответстствует константному ответу, а в каждом звене проверяется значение лишь одного признака (рис. 1). Если в звене проверяется количественный признак, то все значения больше некоего порога отправляются по одному пути, меньше порога - по другому пути. Если это категориальный признак, то одна или несколько категорий отправляется по одному пути, остальные категории по другому пути (категориальные признаки иногда преобразуются в количественные, более подробно рассмотрим позже).

Рис. 1. Пример решающего дерева для задачи бинарной классификации. Принятие решения начинается с верхней вершины графа (корня).

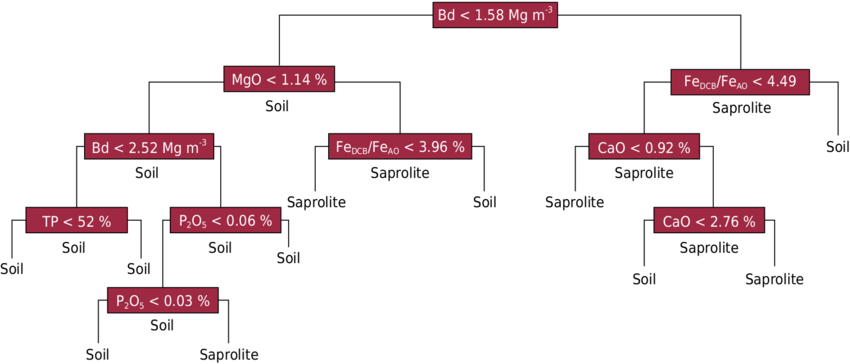
Модели такого вида появились больше полувека назад (Morgan and Sonquist, 1963), и с тех пор практически не изменились. В наши дни одни из наиболее эффективных моделей машинного обучения для работы с табличными данными (scikit-learn, XGBoost, LightGBM, CatBoost) основаны на суммировании предсказаний множества решающих деревьев.

С первого взгляда кажется, что такой подход хорошо подходит для одних задач, но очень плохо подходит для других задач.

Позитивный пример. Многие способы принятия решений выглядят как блок-схема. Например при постановке диагноза врач сначала может измерить температуру. Если температура выше определенного порога, то может заподозрить простуду и посмотреть горло, послушать легкие и так далее. Листьями решающего дерева окажутся конкретные диагнозы. В целом, решающее дерево хорошо следует идее о том, что на некоторые признаки нужно обращать внимание только при условии определенных значений других признаков.

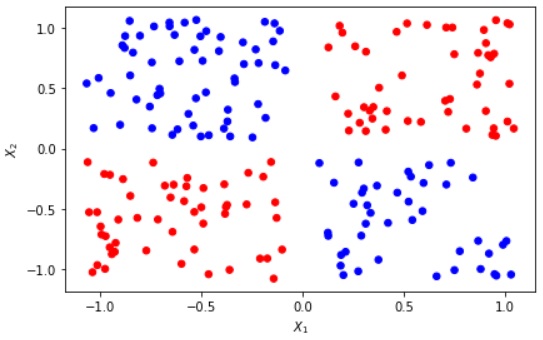
Негативный пример. Попробуем аппроксимировать функцию (рис. 2a) решающим деревом (рис. 2b). Решающее дерево разбивает все пространство признаков на прямоугольные области, в каждой из которых ответом является константа. В данной задаче такой подход явно неоптимален. Во-первых, если решающее дерево представить в виде функции , то эта функция будет разрывной (кусочно-постоянной), тогда как целевая функция непрерывна. Во-вторых, на ответ влияет разность , а в каждом звене дерева проверяется либо , либо , что тоже неоптимально. Для достижения хорошей точности потребуется большое и сложное дерево, хотя сама задача определения очень проста. И наконец, поскольку решающее дерево обучается на данных (о способе обучения мы поговорим далее), то в тех областях, где мало данных или они вовсе отсутствуют, функция будет продолжена неправильно (проблема экстраполяции).

Рис. 2. Приближение непрерывной функции одним решающим деревом и ансамблем решающих деревьев.

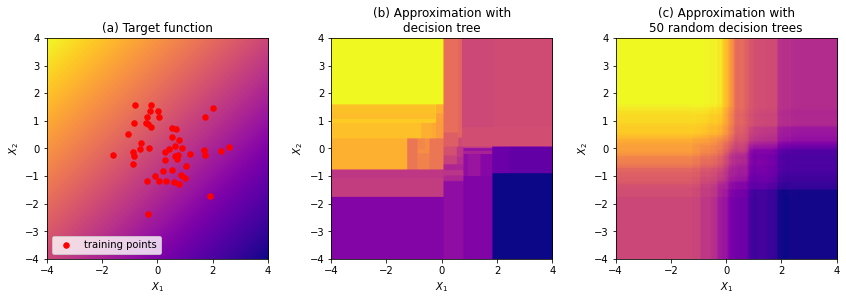
Проблему разрывности функции и негладкости границ между листьями можно смягчить, если обучать не одно решающее дерево, а много деревьев, и усреднять их ответы (рис. 2c). При этом деревья либо должны обучаться на разных подвыборках данных, либо сам процесс обучения должен содержать элемент случайности, чтобы деревья получились неодинаковыми. Поэтому на практике обучают так называемый "случайный лес" из множества деревьев с помощью алгоритмов бэггинга или бустинга, которые мы расмотрим позже. Проблема экстраполяции при этом все же остается - например, случайный лес не может предсказывать значения, большие или меньшие всех тех, что встречались при обучении.

На нашей модельной задаче (рис. 2) решающие деревья дают не впечатляющий результат, тогда как, например, нейронная сеть в этой же задаче обучается почти точно аппроксимировать целевую функцию. Но на реальных задачах, наоборот, ансамбли решающих деревьев сейчас являются одними из самых эффективных моделей.

While deep learning models are more appropriate in fields like image recognition, speech recognition, and natural language processing, tree-based models consistently outperform standard deep models on tabular-style datasets where features are individually meaningful and do not have strong multi-scale temporal or spatial structures. (Lundberg et al., 2019)

Обучение решающих деревьев

Допустим мы имеем обучающую выборку из пар $\{x_i, y_i\}_{i=1}^N$ и хотим построить по нему решающее дерево. Можно без труда построить сколько угодно деревьев, дающих на обучающей выборке 100%-ю точность (если в ней нет примеров с одинаковыми , но разными ). Для этого достаточно в каждой вершине выбирать для разделения любой признак и любой порог, и тогда рано или поздно все примеры попадут в разные листья. Но нам важна не точность на обучающей выборке, а степень обобщения - то есть точность на всем порождающем распределении, из которого взята обучающая выборка.

Можно воспользоваться принципом бритвы Оккама, который говорит, что простые гипотезы предпочтительнее сложных, и попробовать построить как можно более простое дерево. Однако задача нахождения наиболее простого решающего дерева для данного датасета (по суммрному количеству листьев или по средней длине пути в графе) является NP-полной (Hancock et al., 1996; Hyafil and Rivest, 1976), то есть (если $P \neq NP$ ) экспоненциально сложной.

Вообще многие задачи являются экспоненциально сложными, если искать лучшее решение из всех возможных, то есть выполнять исчерпывающий поиск (exhaustive search). Но это не мешает находить хорошие приближенные решения, выполняя либо жадный поиск (greedy search), либо лучевой поиск (beam search). Жадный поиск означает, что на каждом шаге мы ищем локально оптимальное решение, то есть решение, приводящее к наибольшему "сиюминутному" выигрышу. Например, знакомясь с девушкой, которая вам нравится, вы не можете перебрать все возможные варианты развития диалога и заранее выбрать наилучший (т. е. выполнить исчерпывающий поиск), но можете после каждой фразы искать оптимальное продолжение диалога (жадный поиск).

Примечание: пока работаем с количественными признаками, работу с категориальными признаками рассмотрим позднее.

Построение решающего дерева

Применительно к решающим деревьям жадный поиск означает, что мы строим дерево пошагово, на каждом шаге заменяя один из листьев на разделяющее правило, ведущее к двум листьям. На каждом шаге мы должны выбрать:

Лист , который заменяем решающим правилом
Способ разделения (признак и порог)
Значения и $C^\prime$ на двух новых листьях

Этот выбор мы должны сделать так, чтобы функция потерь всего дерева на обучающей выборке уменьшилась как можно сильнее. Для этого достаточно рассмотреть функцию потерь на примерах из обучающей выборки, которые относятся к листу .

Шаг алгоритма выглядит следующим образом: мы перебираем все возможные листья, признаки и пороги (если обучающая выборка имеет размер , то каждый признак принимает не более различных значений, поэтому для каждого признака имеет смысл перебирать не более порогов). Для каждого листа, признака и порога определяем значения и $C^\prime$ на листьях и считаем функцию потерь получившегося дерева. В итоге мы выбираем тот лист, признак и порог, для которых значение функции потерь наименьшее, и дополняем дерево новым разделяющим правилом.

Осталось ответить на вопрос: как именно определяются значения и $C^\prime$ на двух новых листьях?

Пусть после добавления разделяющего правила в один лист попало примеров со значениями целевого признака $y_1, \dots, y_{N_1}$ , в другой лист попало примеров со значениями целевого признака $y^\prime_1, \dots, y^\prime_{N_2}$ . Запишем суммарную функцию потерь после разделения, и минимизируем ее по и $C^\prime$ :

$\sum\limits_{i=1}^{N_1} {Loss}(y_i, C) + \sum\limits_{i=1}^{N_2} {Loss}(y^\prime_i, C^\prime) \to \underset{C, C^\prime}{\min} \tag{1}$

Первое слагаемое зависит только от , второе только от $C^\prime$ , поэтому их можно минимизировать независимо по и $C^\prime$ , если известны примеры, попавшие в один и в другой лист.

Оптимальное разделение в задаче регрессии

В качестве функции потерь выберем среднеквадратичную ошибку. Исходя из формулы , на первом листе нужно выбрать такое значение на первом листе, что:

$\sum\limits_{i=1}^{N_1} (C - y_i)^2 \to \underset{C}{\min}$

Поскольку - константы, то задача означает поиск минимума функции от одной переменной. Взяв производную и приравняв ее к нулю мы найдем, что - среднее арифметическое значений . Аналогично, $C^\prime$ - среднее арифметическое значений $y_i^\prime$ .

Если бы мы минимизировали не среднеквадратичную ошибку (MSE), а среднюю абсолютную ошибку (MAE), тогда оптимальным значением была бы медиана значений .

Оптимальное разделение в задаче классификации

Мы можем пойти стандартным путем: пусть каждый лист выдает вероятности классов, а в качестве функции потерь используем категориальную перекрестную энтропию (logloss). Пусть количество классов равно . Введем следующие обозначения:

$\{p_k\}_{i=1}^{K}$ - доля объектов -го класса в первом листе
$\{p_k^\prime\}_{i=1}^{K}$ - доля объектов -го класса во втором листе
$\{C_k\}_{i=1}^{K}$ - предсказываемая вероятность -го класса в первом листе
$\{C_k^\prime\}_{i=1}^{K}$ - предсказываемая вероятность -го класса во втором листе

Минимизируем суммарную ошибку на первом листе. Количество примеров в первом листе, для которых верным ответом является класс , равно . Суммируем ошибку по всем классам и будем искать минимум по $C_1, \dots, C_K$ :

$- \sum\limits_{k=1}^{K} N_1 p_k \log C_k \to \underset{C_1, \dots, C_K}{\min} \qquad \sum\limits_{k=1}^{K} C_k = 1$

Из данной формулы можно исключить , и тогда задача нахождения оптимального распределения сводится к минимизации перекрестной энтропии между распределениями и . Это эквивалентно минимизации расхождения Кульбака-Лейблера между и и достигается при для всех . Полученный результат интуитивно понятен: если, например, в листе 10% примеров класса 0 и 90% примеров класса 1, то предсказывая ответ для неизвестного примера оптимальным вариантом будет назначить классам вероятности 10% и 90%.

Таким образом, мы нашли, что оптимальное равно . Суммарная функция потерь на обоих листьях будет равна:

$- N_1 \sum\limits_{k=1}^{K} p_k \log p_k - N_2 \sum\limits_{k=1}^{K} p_k^\prime \log p_k^\prime = N_1 H(p_k) + N_2 H(p_k^\prime)$

Здесь - энтропия распределения (ее более корректно записывать как $H(\{p_k\}_{i=1}^{K})$ ). Иными словами, нам нужно искать такой признак и порог, чтобы минимизировать взвешенную сумму энтропий распределений классов в обоих листьях. Энтропию можно интерпретировать как степень неопределенности, или "загрязненности" (impurity) распределения, и энтропия достигает минимума в том случае, если распределение вероятностей назначает вероятность 1 одному из классов.

Минимизация взвешенной суммы энтропий называется энтропийным критерием разделения (рис. 3). Интересно, что если мы будем минимизировать не кроссэнтропию, а среднюю абсолютную ошибку (MAE) между предсказанным распределением и истинным (эмпирическим) распределением, которое назначает вероятность 1 верному классу, то придем к критерию Джини:

$N_1 \sum\limits_{k=1}^{K} p_k (1 - p_k) + N_2 \sum\limits_{k=1}^{K} p_k^\prime (1 - p_k^\prime) \to \min$

На практике чаще используется энтропийный критерий, потому что он соответствует перекрестной энтропии, которая чаще других применяется в задачах классификации.

Рис. 3. Распределение классов до и после разделения. Второй способ разделения (c) дает больший выигрыш по энтропийному критерию, чем первый способ (b).

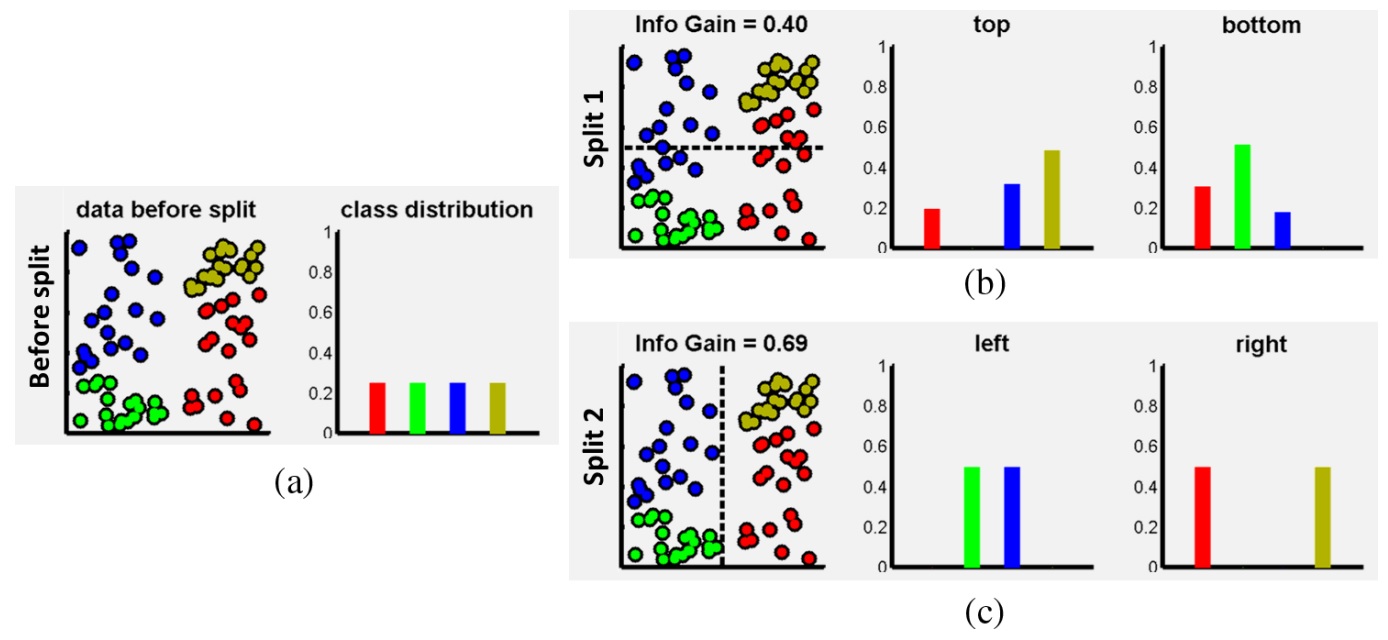
Критерий остановки и обрезка дерева

Мы рассмотрели шаг роста дерева, но остается еще один вопрос: до какой степени нужно растить дерево? На рис. 3 показаны шаги роста дерева для классификации по энтропийному критерию. На первых шагах дерево находит явные закономерности в распределении классов, но затем начинает переобучаться на случайном шуме. Говоря в терминах так называемой дилеммы смещения-дисперсии, дерево неограниченной глубины имеет высокую дисперсию, то есть получаемый результат сильно зависит от случайных изменений в обучающей выборке (например, мы удалили часть примеров или добавили новые).

Если мы соберем ансамбль из деревьев, то проблема переобучения ослабнет. Однако чем больше дерево, тем больше вычислительных ресурсов требуется для его обучения, поэтому размер дерева в ансамбле все же имеет смысл ограничивать.

Рис. 3. Обучение решающих деревьев в зависимости от максимального количества листьев.

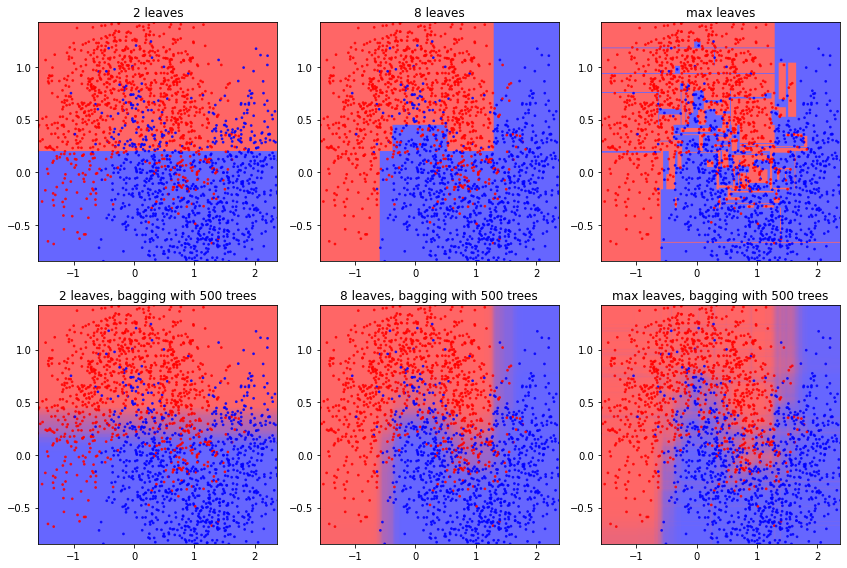
На практике чаще ограничивают не суммарное количество листьев, а максимальную глубину дерева, то есть максимальную длину пути от корня к листу. Можно также воспользоваться следующим критерием: прекращать рост дерева, если после добавления нового разделяющего правила функция потерь упала на величину, меньшую некоего порога. Однако такой подход тоже имеет свои проблемы.

На рис. 4а показана ситуация, когда добавление первого оптимального разделяющего правила не приведет к значимому снижению ошибки классификации, тогда как следующие два разделяющих правила ведут к радикальному снижению функции потерь. Более того, оптимальное значение порога для первого разделяющего правила сильно зависит от случайных факторов и может быть выбрано не равным нулю. На этом примере мы видим ситуацию "отложенного выигрыша", когда жадный алгоритм построения дерева может сработать не лучшим образом (см. также Biau et al., 2008, раздел 6).

Рис. 4. Первое решающее правило не даст выигрыша в точности.

Обрезкой решающего дерева (pruning) называется процесс удаления из него отдельных ветвей, которые не приводят к существенному падению функции потерь. Имеел ли смысл сначала строить, а затем удалять ветви? Как мы увидели на рис. 4, при построении ветви мы не можем точно сказать, насколько сильно эта ветвь и дочерние к ней ветви помогут снизить функцию потерь. Это станет понятно только тогда, когда мы построим дочерние ветви, затем дочерние к дочерним и так далее. Если даже после этого функцию потерь на данной ветви не удалось сушественно снизить, тогда всю ветвь можно удалить, упростив дерево. См. также Соколов, 2018, раздел 5.

Работа с категориальными признаками

До сих пор мы рассматривали работу только с количественными признаками. Если в обучающей выборке примеров, то в количественном признаке имеет смысл перебирать не более значений порога. Теперь рассмотрим категориальный признак с категориями. Можно разделить все категории на два подмножества, и отправить эти подмножества в разные ветви. Но количество возможных делений всех категорий на два подмножества растет экспоненциально с ростом количества категорий , что делает невозможным полный перебор при большом .

Есть два достаточно простых пути. Мы можем закодировать категориальный признак one-hot кодированием. Тогда если по этому признаку произойдет деление, то одна категория отправится в одву ветвь, все остальные в другую, то есть мы ищем только деления вида "одина категория против всех". Также мы можем оставить признаки в label-кодировании и рассматривать их как количественный признак, тогда в одну из ветвей отправятся все категории, индексы которых меньше определенного числа. Такие деления получаются менее осмысленными, но из этого напрямую не следует, что эффективность такого подхода будет ниже. Могут быть и другие подходы, например мы можем перебрать какое-то количество случайных делений всех категорий на два подмножества или упорядочить категории по среднему значению целевой переменной и искать разбиение как для количественного признака (см. Соколов, 2018, раздел 7).

На практике установлено, что для категориальных признаков небольшой размерности (т. е. с небольшим количеством категорий) лучше работает one-hot кодирование (см. Prokhorenkova et al., 2017). Для признаков большой размерности можно тоже применять one-hot кодирование, хотя если сделать это в явном виде, то получившаяся матрица признаков будет занимать очень много места в памяти. Более эффективным подходом к работе с категориальными признаками большой размерности считается target-кодирование.

При target-кодировании мы заменяем каждую категорию некой статистикой (обычно средним значением) целевой переменной, рассчитанной по объектам данной категории. Например, если категориальной переменной является модель автомобиля, а целевым признаком является цена, то мы рассчитываем среднюю цену по каждой модели, и используем полученные данные вместо модели автомобиля.

Данный подход имеет два недостатка. Во-первых, представим, что в каждой категории только один объект. Тогда после target-кодирования признак будет содержать готовые ответы. Модели, обучаемой на этом датасете, будет достаточно извлекать ответ из этого признака, не используя никакие другие признаки. Очевидно, такой подход приведет к переобучению. Как вариант, можно использовать две обучающие выборки: на первой рассчитывать статистику по целевой переменной, а на второй с помощью этой статистики делать target-кодирование и обучать модель.

Вторая проблема в том, что категориальные признаки могут влиять на целевой признак не независимо друг от друга. Например, пусть мы имеем два категориальных признака в label-кодировани, принимающие значения 0 или 1: если они не равны друг другу, то целевой признак равен 1, в противном случае целевой признак равен 0. Если мы выполним target-кодирование, то эта информация будет полностью утеряна.

Несмотря на эти недостатки, target-кодирование и его различные варианты остается одним из самых эффективных способов работы с категориальными признаками высокой размерности. Авторы библиотеки CatBoost разработали метод упорядоченного target-кодирования, при котором на обучающих примерах задается некий порядок, и для каждого -го примера статистика по целевой переменной рассчитывается только на основе примеров с индексами меньше (см. далее в разделе "CatBoost: несмещённый упорядоченный бустинг"). Обзор различных способов target-кодирования также можно найти в Pargent et al., 2021.

Другие особенности решающих деревьев

Одним из преимуществ решающих деревьев является отсутствие необходимости нормализации данных и в целом почти полная нечувствительность к монотонным преобразованиям количественных признаков (например, логарифмированию).

Еще одним преимуществом является простота работы с пропущенными значениями. При вычислении суммарной функции потерь мы можем игнорировать те объекты, для которых значение признака не указано. Далее при построении дерева эти объекты можно отправять одновременно в обе ветви. При инференсе (то есть получении предсказаний с помощью уже построенного дерева) можно также отправлять объекты с неизвестным значением признака одновременно в обе ветви, и в обоих ветвях рассчитывать целевую переменную. После этого мы усредняем оба значения с весами, равными количеству обучающих примеров, прошедших через обе ветви (подробнее см. Соколов, 2018).

Ансамблирование решающих деревьев

Выше мы видели (рис. 2, 3), что одно решающее дерево имеет достаточно грубые границы между листьями, и при этом либо существенно недообучается (при малом количестве листьев), либо сильно переобучается (при большом количестве листьев). Эту проблему можно исправить, обучая сразу много разных решающих деревьев.

В целом ансамблированием называется комбинация нескольких моделей машинного обучения в одну модель. Ансамблирование решающих деревьев как правило осуществляется "одноуровнево", то есть при инференсе все деревья работают параллельно и независимо выдают ответ, а затем их предсказания складываются или усредняются. Процесс обучения при этом может выполняться параллельно (бэггинг) или последовательно (бустинг).

Существует также стекинг, при котором предсказания одной модели используются в качестве входных данных для другой модели. Однако распространенные алгоритмы ансамблирования решающих деревьев (random forest, XGBoost, LightGBM, CatBoost) не включают в себя стекинг. Стекинг может выполняться поверх этих моделей, так же как и поверх любых других (нейронных сетей и пр.).

Бэггинг

Алгоритм бэггинга достаточно прост: каждое дерево обучается на своей подвыборке данных, взятой из обучающей выборки. Подвыборка делается с возвращением, то есть один пример может быть выбран более одного раза. Если при этом в каждом дереве мы также будем использовать случайную подвыборку признаков, то получим алгоритм построения случайного леса, реализованный, например, в sklearn. Можно внести еще больше случайности в процесс ансамблирования, если процесс построения дерева также будет содержать элементы случайности (см. Extremely Randomized Trees).

Бустинг

Более распространенным методом ансаблирования решающих деревьев является бустинг. Бустинг - это способ построения ансамбля, в котором обучается много копий более слабой модели ("weak learner"), то есть такой модели, которая не может достичь высокой точности на обучающем датасете, переобучившись на нем. Как правило такой моделью является решающее дерево небольшой глубины. На каждом шаге новый weak learner концентрируется на исправлении ошибок, допущенных предыдущими weak learner'ами. В итоге предсказания всех weak learner'ов суммируются с определенными весами. Бустинг чем-то похож на бэггинг, но в бэггинге модели обучаются совершенно независимо и параллельно, а в бустинге последовательно, с оглядкой на предыдущие.

Ранний вариант бустинга: AdaBoost

Итак, в бустинге каждый следующий weak learner стремится скорректировать предсказания предыдущих. Это можно сделать разными способами. Одной из первых эффективных реализаций бустинга был AdaBoost - в нем каждый следующий weak learner фокусировал внимание на тех примерах, на которых предыдущие weak learner'ы дали неверные ответы. При этом он не знал, какие именно ответы даны предыдущими weak learner'ами - было лишь известно, что ответы неверны или неточны. Задачей нового weak learner'а было дать верные ответы преимущественно на этих примерах.

Заметим, что при этом не используется никакого валидационного датасета. Используется только обучающий датасет, на нем же оценивается точность предыдущих weak learner'ов. Это означает, что если очередной weak learner после обучения дал верные ответы на все примеры, то бустинг продолжить будет невозможно. Например, если в качестве weak learner'а мы используем решающее дерево неограниченной глубины, то так и произойдет. Нужно использовать решающие деревья небольшой глубины: weak learner должен быть действительно "слабым", не переобучаясь слишком сильно.

Градиентный бустинг

В градиентном бустинге (Friedman, 2001) целевыми данными для следующего weak learner'а является градиент (со знаком минус) функции потерь по предсказаниям предыдущих алгоритмов. Таким образом следующий weak learner корректирует предсказания предыдущих.

Например, производная среднеквадратичной ошибки $(y - \hat{y})^2$ по $\hat{y}$ равна $2(\hat{y} - y)$ , а значит предсказывая градиент weak learner как раз и предсказывает разность предсказания и правильного ответа. Но можно использовать и другие функции потерь.

Далее рассмотрим алгоритм градиентного бустинга более формально. Для дальнейшего изложения введем необходимые обозначения:

Обучающая выборка (датасет) состоит из массива исходных данных $\textbf{X} = \{x_i\}_{i=1}^N$ и массива эталонных ответов $\textbf{y} = \{y_i\}_{i=1}^N$ . Каждый представляет собой набор признаков - вектор фиксированной длины. В задаче классификации будем считать, что $\textbf{y}$ представлен в one-hot кодировании.
Обучаемый алгоритм имеет параметры $\theta$ , принимает на вход исходные данные и возвращает предсказания: $f(x_i, \theta) = \hat{y}_i$ . Массив предсказаний алгоритма на всей обучающей выборке обозначим как $\hat{\mathbf{y}} = f(\textbf{x}, \theta)$ . Количество параметров может быть как фиксированным (например, нейронная сеть), так и переменным (например, растущий случайный лес). Предсказание может быть, а может не быть дифференцируемым по параметрам $\theta$ . Для градиентного спуска требуется дифференцируемость по параметрам, для градиентного бустинга - не требуется.
Функция потерь принимает на вход эталонный ответ и предсказание и выдает число: $loss(y_i, \hat{y}_i)$ . Мы хотим минимизировать сумму значений функции потерь по всей обучающей выборке: $sum\_loss(\textbf{y}, \hat{\mathbf{y}}) = \sum_{i=1}^{n} loss(y_i, \hat{y}_i)$ . Как для градиентного спуска, так и для градиентного бустинга требуется дифференцируемость функции потерь по предсказаниям.

Алгоритм градиентного бустинга

Пусть мы имеем обучающую выборку, обучаемый алгоритм (weak learner) и функцию потерь. В качестве исходного приближения выберем константу так, чтобы сумма $\sum_{i=1}^n loss(y_i, C)$ была минимальна. К начальному приближению мы будем прибавлять предсказания weak learner'ов.
Заранее выберем число шагов .

for k = 0, ..., N-1:

На -м шаге мы уже обучили weak learner'ов. Мы получаем предсказания с помощью их взвешенной суммы для всех примеров из обучающего датасета: $\hat{y}_i = С + \sum\limits_{j=0}^k w_i f(x_i, \theta_j)$
Считаем производную функции потерь со знаком минус по каждому предсказанию: $r_i = -\cfrac{\partial}{\partial \hat{y}_i} loss(y_i, \hat{y}_i)$ . Таким образом мы получаем информацию о том, как нам нужно изменить каждое предсказание, чтобы функция потерь уменьшилась (исходя из смысла понятия производной).
Обучаем новый weak learner предсказывать по . Обозначим параметры нового weak learner'а за $\theta_k$ .
Осталось выбрать вес для нового weak learner'а. Для этого получаем предсказания нового weak learner'а на всей обучающей выборке: $\hat{r}_i = f(x_i, \theta_k)$ . Затем подбираем такой вес , чтобы значение $sum\_loss(\mathbf{y}, \hat{\mathbf{y}} + w_k*\hat{\mathbf{r}})$ было минимально.

В итоге мы получаем ансамбль из weak learner'ов. Алгоритм инференса (то есть предсказания на произвольных данных) выглядит аналогично:

$\hat{y} = С + \sum_{j=0}^N w_i f(x, \theta_j)$

Про градиентный бустинг см. также в этом посте на Хабре.

Регуляризация градиентного бустинга

Для того, чтобы ослабить переобучение градиентного бустинга, применяются следующие техники:

Subsampling. Мы обучаем каждый следующий weak learner не на всей обучающей выборке, а на случайной подвыборке. В этом случае градиентный бустинг называется стохастическим.

Shrinkage. После того, как мы расчитали вес нового weak learner'а , мы умножаем его на некоторое число меньше 1 (learning rate). Таким образом мы укорачиваем шаг в направлении градиента.

Регуляризация weak learner'а. Например, в sklearn можно использовать параметр max_features, который определяет, сколько случайно выбранных признаков будет использоваться при поиске оптимального разбиения в каждом узле дерева.

Особенности градиентного бустинга

В случае выбора функции потерь ее производная пропорциональна разности предсказания и верного ответа, поэтому градиентный бустинг сводится к тому, что каждый следующий weak learner пытается предсказать величину ошибки, допущенную предыдущим. Но при этом сам допускает ошибки, и их пытается предсказать уже следующий weak learner, и так далее.

Важно, чтобы weak learner не был способен слишком сильно переобучиться, иначе следующим weak learner'ам будет не на чем учиться. Поэтому в качестве weak learner'а обычно выбирают деревья небольшой глубины. Линейная регрессия не подходит в качестве weak learner'а, поскольку взвешенная сумма линейных моделей линейна, поэтому и весь ансамбль получится линейным.

Интересно, что если мы выберем в градиентном бустинге специальную "экспоненциальную" функцию потерь, то мы получаем алгоритм, эквивалентный AdaBoost. Конечно с вычистельной точки зрения эти алгоритмы получатся все равно разные, но было доказано, что они эквивалентны в плане получаемого результата. Таким образом, алгоритм AdaBoost эквивалентен частному случаю градиентного бустинга.

Связь с градиентным спуском

Идея как градиентного спуска, так и градиентного бустинга состоит в том, что мы рассчитываем градиент функции потерь по предсказаниям, а затем ходим сдвинуть предсказания в направлении, противоположном градиенту, и таким образом сделать их более точными.

Но в градиентном спуске это достигается с помощью распространения градиента на веса и обновления весов, а в градиентном бустинге с помощью прибавления предсказаний нового weak learner'а, который аппроксимирует градиент со знаком минус. Таким образом, в градиентном спуске используется фиксированное число параметров, а в градиентном бустинге - переменное (каждый новый weak learner содержит новые параметры).

Иногда градиентный бустинг рассматривают как покоординатный градиентный спуск в пространстве функций.

XGBoost

Теперь рассмотрим современные алгоритмы бустинга над решающими деревьями, и начнем с XGBoost.

Библиотека XGBoost (Chen and Guestrin, 2016) является вычислительно эффективной реализацией градиентного бустинга над решающими деревьями. Помимо оптимизированного программного кода, авторы предлагают различные улучшения алгоритма.

Рассмотрим для примера задачу регрессии и введем следующие обозначения:

$\{x_i, y_i\}_{i=1}^N$ - обучающая выборка
- количество деревьев в ансамбле
$f_k: x \to y$ - k-e дерево ансамбля как функция
$F: x \to y$ - весь ансамбль как функция
${loss}: y_{true} \times y_{pred} \to \mathbb{R}$ - выбранная пользователем основная функция потерь
- количество листьев в -м дереве ансамбля
- вектор, составленный из выходных значений на всех листьях -го дерева

В XGBoost ответы суммируются по всем деревьям ансамбля:

$F(x) = \sum\limits_{k=1}^K f_k(x)$

Суммарная функция потерь в XGBoost выглядит следующим образом:

${total\_loss} = \sum\limits_{i=1}^N {loss}(y_i, F(x_i)) + \gamma\sum\limits_{k=1}^K T_k + \frac{1}{2}\lambda\sum\limits_{k=1}^K \|w_k\|^2$

Здесь $\gamma$ , $\lambda$ - гиперпараметры. Первое слагаемое - это основная функция потерь, второе слагаемое штрафует деревья за слишком большое количество листьев, третье слагаемое за слишком большие предсказания. Третье слагаемое является нетипичным в машинном обучении. Оно обеспечивает то, что каждое дерево вносит минимальный вклад в результат. Функция потерь используется при построении каждого следующего дерева, то есть функция потерь оптимизируется по параметрам лишь последнего дерева, не затрагивая предыдущие. Для минимизации ${total\_loss}$ используется метод второго порядка, то есть рассчитываются не только производные, но и вторые производные функции потерь по предсказаниям предыдущих деревьев (подробнее см. Chen and Guestrin, 2016, раздел 2.2).

При поиске каждого нового разделяющего правила, для каждого признака перебираются не все возможные значения порога, а значения с определенным шагом. Для этого на признаке рассчитывается набор персентилей, используя статистику из обучающего датасета. Поиск оптимального порога выполняется только среди этих персентилей. Это позволяет существенно сократить время перебора и ускорить обучение. Для работы с пропущенными значениями в каждом решающем правиле определяется ветвь, в которую будут отправлены объекты с пропущенным значением данного признака.

Однако основной ценностью библиотеки XGBoost является эффективная программная реализация. За счет разных оптимизаций, таких как эффективная работа с пропущенными значениями, поиск порога только среди персентилей, оптимизация работа с кэшем и распределенное обучение, достигается выигрыш в десятки или даже сотни раз по сравнению с наивной реализацией.

CatBoost: несмещённый упорядоченный бустинг

Библиотека CatBoost (Prokhorenkova et al., 2017; Dorogush et al, 2018) - еще одна эффективная реализация градиентного бустинга над решающими деревьями. Основные особенности алгоритма следующие (не в порядке важности):

Использование решающих таблиц (разновидности решающих деревьев)
Упорядоченное target-кодирование на категориальных признаках высокой размерности
Бустинг с упорядочиванием обучающих примеров

Упорядоченное target-кодирование

Упорядоченное target-кодирование мы уже кратко рассматривали в разделе "Работа с категориальными признаками". Рассмотрим некий категориальный признак . Все обучающие примеры случайным образом упорядочиваются. Пусть -й пример имеет категорию . Для данного примера рассчитывается выбранная статистика целевой переменной для всех примеров с индексами строго меньше , имеющими ту же категорию . Полученное значение является новым признаком, который используется вместо исходного признака . О том, какие статистики можно использовать, см. документацию CatBoost (1, 2).

В таком подходе есть одна проблема: статистика целевой переменной на первых примерах будет рассчитана слишком неточно (будет иметь высокую дисперсию). Поэтому в CatBoost target-кодирование выполняется несколько раз, каждый раз с новым случайным упорядочиванием обучающей выборки.

Использование решающих таблиц

Решающая таблица является частным случаем забывчивого решающего дерева (oblivious decision tree). В таком дереве все решающие правила одного уровня (то есть на одном и том же расстоянии от корня) проверяют один и тот же признак (Kohavi, 1994; Rokach and Maimon, 2005). Забывчивые решающие деревья разрабатывались для задач с большим количеством нерелевантных признаков.

В варианте, реализованном в CatBoost, на каждом уровне решающего дерева используется не только общий признак, но и общий порог разделения (аналогично Modrý and Ferov, 2016). Благодаря этому порядок следования разделяющих правил становится не важен: можно переставить уровни дерева, и его функционирование от этого не изменится. Такое дерево более естественно представлять в виде таблицы, в которой решающее правило соответствует колонке, в которой может быть значение 0 или 1. Если в дереве уровней , то в таблице колонок и строк, содержащих все возможные сочетания значений колонок. Каждой строке сопоставляется константное значение целевого признака. Как можно видеть, такая модель имеет достаточно слабое сходство с обычным решающим деревом, хотя и строится по тем же правилам.

На рис. 5 показана работа CatBoost на примере задачи регрессии (сравните с рис. 2).

Рис. 5. Приближение непрерывной функции одной или несколькими решающими таблицами с помощью CatBoost.

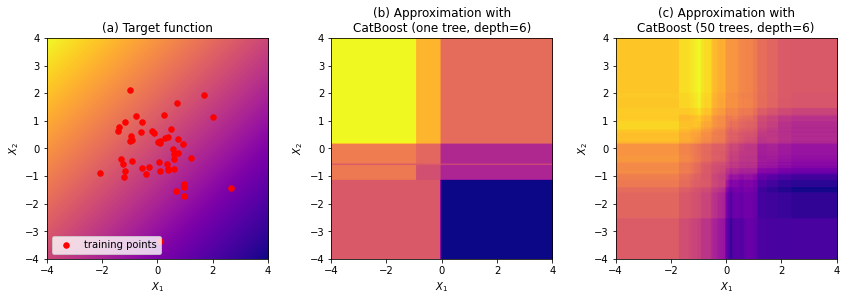
Несколько решающих таблиц можно объединить в одну, поэтому весь ансамбль CatBoost можно представить в виде одной решающей таблицы, что видно из рис. 5. При этом не любая сложная решающая таблица может быть разложена в сумму многих простых таблиц.

Впрочем, CatBoost поддерживает не только решающие таблицы, но и обычные решающие деревья (см. параметр grow_policy). Возможно, мотивацией использовать именно решающие таблицы была скорость инференса. Как говорит один из разрабочиков библиотеки Станислав Кириллов:

Мы изначально создавали его [CatBoost] как библиотеку для применения в сервисах Яндекса, отсюда характерные для большой компании требования. К примеру, у наших сервисов всегда высокие нагрузки, поэтому скорость инференса модели критична для CatBoost. (habr)

В чем профит наших oblivious-деревьев? Они быстро учатся, быстро применяются и помогают обучению быть более устойчивым к изменению параметров с точки зрения изменений итогового качества модели, что сильно уменьшает необходимость в подборе параметров. (habr)

Проблема смещённости бустинга

Алгоритм бустинга имеет одну достаточно очевидную проблему. Выполняя шаг бустинга, мы хотим скорректировать предсказания алгоритма , обучив новый алгоритм , то есть алгоритм должен выявить и исправить систематические ошибки, допущенные алгоритмом . При этом для обучения мы используем те же обучающие данные , что использовали для обучения . Это означает, что мы оцениваем работу алгоритма (точнее, производные функции потерь по его предсказаниям) на тех же данных, на которых этот алгоритм обучался. Однако алгоритм переобучился на данных , и его работа на этих данных уже не показательна.

Gradients used at each step are estimated using the same data points the current model was built on. This leads to a shift of the distribution of estimated gradients in any domain of feature space in comparison with the true distribution of gradients in this domain, which leads to overfitting. The idea of biased gradients was discussed in previous literature [1] [9]. (Dorogush et al, 2018, раздел 3)

Рассмотрим эту проблему более формально. Обозначим на порождающее распределение, из которого взята обучающая выборка. Совместное распределение в обучающей выборке можно обозначить за $P_{train}$ (эмпирическое распределение). Алгоритм моделирует условное распределение , алгоритм обучается моделировать условное распределение производных:

$P(g(x, y)|x) = P(\cfrac{\partial {Loss}(y, F(x))}{\partial F(x)}|x)$

Целью является моделирование для всего порождающего распределения, то есть при $x, y {\sim} P$ , однако мы имеем выборку из только для обучающих данных, то есть при $x, y {\sim} P_{train}$ . Проблема заключается в том, что распределение производных на обучающей выборке $P_{train}$ является смещённым (biased), проще говоря искаженным, относительно распределения производных на всем порождающем распределении :

$g(x, y) | x, y {\sim} P \neq g(x, y) | x, y {\sim} P_{train}$

В качестве примера, если максимально переобучился на $P_{train}$ , то $g(x, y) | x, y {\sim} P \equiv 0$ . Из-за этого получается не оптимальным, так как обучается на выборке не из того распределения, которое в идеале должен моделировать. В идеале хотелось бы использовать для оценки градиента данные, на которых алгоритм не обучался, но тогда нам нужно использовать новые данные на каждом шаге бустинга, что невозможно при большом числе шагов.

Можно привести еще такой пример. Представим, что ученик обучается решать математические задачи из класса (например, упрощение дробей), имея выборку из этих задач $P_{train}$ , и у нас есть также тестовая выборка задач $P_{test}$ . Часть примеров из $P_{train}$ ученик не понял и просто запомнил, но не идеально. Если после обучения ученика дать ему задачи из $P_{test}$ , которые он никогда не видел, то часть задач он решит, на на других сделает на них какие-то осмысленные ошибки. Если же дать ученику снова решать задачи из $P_{train}$ , то он будет пытаться вспомнить решение, и сделает во-первых меньше ошибок, во-вторых уже ошибки другого рода (неправильно вспомнит и напишет что-то бессмысленное, что сойдется с ответом). Это означает, что распределение ошибок может быть совсем разным на обучающих и тестовых данных, по причине переобучения и так называемой утечки данных (target leakage).

Несмотря на то, что градиентный бустинг содержит такую проблему, он все равно хорошо работает на практике, поэтому на эту проблему долгое время закрывали глаза. Авторы библиотеки CatBoost нашли способ ее решения, названный упорядоченным бустингом.

Упорядоченный бустинг

В Prokhorenkova et al., 2017 (раздел 4) упорядоченный бустинг описывается в двух вариантах. В первом варианте на каждом шаге бустинга обучается сразу много деревьев (подробнее рассмотрим далее), но тогда вычислительная сложность алгоритма многократно растет. Во втором варианте на каждом шаге обучается только одно дерево, как и в обычном бустинге. В обоих случаях авторы доказывают несмещенность получаемой оценки градиента.

Рассмотрим сначала первый вариант упорядоченного бустинга. Введем на обучающих примерах некий порядок (так же, как в упорядоченном target-кодировании) и пронумеруем их согласно этому порядку: $\mathcal{D} = \{x_i, y_i\}_{i=1}^N$ . На каждом шаге бустинга мы будем обучать не одно решающее дерево, а набор решающих деревьев для каждого номера обучающего примера: $f_{i, t}$ . При этом последовательность деревьев для каждого рассматривается как модель градентного бустинга, то есть ответы деревьев суммируются по : $F_{i, t} = f_{i, 0} + \dots + f_{i, t}$ (рис. 6). Таким образом, мы обучаем столько моделей градиентного бустинга, сколько у нас обучающих примеров. При этом -е дерево обучается на примерах с 1-го по -й включительно и на каждом шаге используется для получения предсказания на -м примере.

Рис. 6. Один из вариантов упорядоченного бустинга.

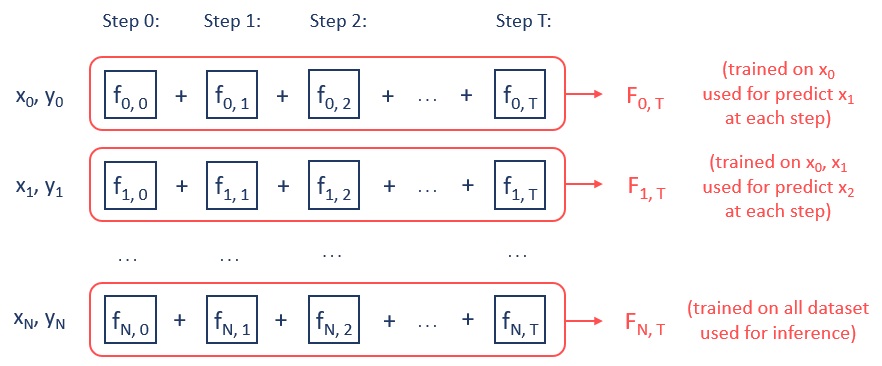
Например, чтобы на 100-м шаге обучить 10-е дерево, нам нужны предсказания для первых 10 примеров. Предсказание для 10-го примера мы получаем 9-й моделью градиентного бустинга (то есть суммируя все деревья, которые обучались на первых 9 примерах), предсказание для 9-го примера мы получаем 8-й моделью градиентного бустинга и так далее. Что делать с первым примером при этом, правда, не уточняется - возможно, ответом на нем всегда является константа.

После шагов бустинга финальным результатом является модель $F_{N, T}$ , то есть та, что обучалась на всех примерах. Эта модель в дальнейшем используется для тестирования и инференса. Те деревья, которые обучались не на всех примерах, после обучения отбрасываются.

В таком алгоритме оценка градиента получается несмещенной, так как деревья не используются для предсказания на тех же примерах, на которых обучались. Однако такой подход не реализуем на практике из-за большого объема вычислений. Можно было бы объединять примеры в группы, и обучать по одному дереву для каждой группы, но все равно на каждом шаге пришлось бы обучать много деревьев. Авторы CatBoost предлагают иной подход, также обладающий свойством несмещенности.

Алгоритм CatBoost

Общая идея алгоритма CatBoost в том, что во-первых мы выполняем упорядоченное target-кодирование, а во-вторых при расчете предсказаний на листьях мы используем примеры с индексами меньше, чем тот пример, на котором хотим получить предсказание.

На каждом шаге бустинга обучается одна решающая таблица (дерево). Глубина дерева является гиперпараметром, то есть задается заранее. Если глубина равна , то дерево представляет собой последовательность из признаков и порогов разделения и имеет листьев.

Далее рассмотрим алгоритм в том виде, в каком он дан в Prokhorenkova et al., 2017, appendix B. Алгоритм CatBoost имеет два режима: plain (бустинг без упорядочивания) и ordered (упорядоченный бустинг), мы рассмотрим только режим ordered.

Примечание. В CatBoost по умолчанию не всегда используется упорядоченный бустинг, см. параметр boosting_type. Также есть возможность использовать разные виды решающих деревьев (см. далее). В данном разделе мы будем рассматривать только использование решающих таблиц.

В качестве входных данных алгоритм принимает обучающую выборку, пронумерованную от до , количество шагов , функцию потерь и два гиперпараметра: $\alpha$ , используемый как learning rate (см. раздел "Регуляризация градиентного бустинга") и - количество перестановок минус единица.

Сначала (строка 1) создаются случайных перестановок, то есть упорядочиваний обучающей выборки (например, см. np.random.permutation). Позицию -го элемента обучающей выборке в перестановке $\sigma_r$ будем обозначать как $\sigma_r(i)$ . Эти перестановки используются как для упорядоченного бустинга, так и для упорядоченного target-кодирования. Перестановки $\sigma_1, \dots, \sigma_s$ будут использоваться для обучения, перестановка $\sigma_0$ будет использоваться для создания финальной модели для инференса.

В обычном градиентном бустинге мы обучаем последовательность деревьев, и на каждом шаге прибавляем предсказания нового дерева к результату. Таким образом, на каждом шаге результатом является новое дерево и предсказаний (для каждого обучающего примера). В CatBoost на каждом шаге тоже обучается одно дерево, но при этом имитируется обучение сразу многих "виртуальных" моделей градиентного бустинга, поэтому на каждом шаге результатом является сразу несколько предсказаний для каждого примера. Эти предсказания хранятся в массиве .

Запись $M_{r, j}(i)$ означает предсказание (в случае регрессии - число), сделанное на -м примере "виртуальной" моделью с индексами . Индекс соответствуют номеру перестановки (при этом - особный случай, когда индекс отсутствует). Идея упорядоченного бустинга в том, что на выборке и на моделях вводится некий порядок (см. раздел "Упорядоченный бустинг"), и индекс соответствует этому порядку. В простом варианте мы использовали столько моделей, сколько есть обучающих примеров (рис. 6). Но из соображений производительности хотелось бы уменьшить количество моделей, поэтому в CatBoost при обучающих примерах используется $\lceil \log_2 n \rceil$ моделей (это и есть диапазон значений для индекса ). Символ $\lceil\ \rceil$ означает округление до целого в большую сторону.

Чтобы лучше понять, почему используется именно $\lceil \log_2 n \rceil$ моделей, представим, что мы имеем 70 обучающих примеров. Мы раскладываем их по мешкам, и в каждый следующий мешок кладем в 2 раза больше примеров, чем в предыдущий. Тогда в мешках окажется 1, 2, 4, 8, 16, 32 и 7 примеров (последний мешок заполнен не полностью). Каждому -му мешку соответствует "виртуальная" модель градиентного бустинга, которая обучается на примерах из мешков с номерами $1, 2, \dots, i$ и используется для предсказания на примерах из -го мешка.

Таким образом, - это массив чисел. Подмассив имеет размерность , подмассив при $r=1, \dots, s$ имеет размерность $\lceil \log_2 n \rceil \times n$ . Последний индекс, соответствующий номеру обучающего примера, записывается в круглых скобках. Например, в задаче регрессии и $M_{1, 0}(0)$ - это числа. В строках 2-4 алгоритма массив инициализируется нулями.

Далее начинается основной цикл из шагов бустинга. В строке 6 строится новое дерево (функцию рассмотрим далее), при этом используется массив предыдущих предсказаний $\{M_r\}_{r=1}^s$ и перестановки $\{\sigma_i\}_{i=1}^s$ , то есть и $\sigma_0$ на этом шаге не используются. Дерево , построенное на шаге , представляет собой последовательность разделяющих правил, каждое из которых состоит из признака и порога. При этом значения на листьях в не указаны (идея в том, что они разные для разных виртуальных моделей).

Функция (строка 7) используется для получения номера листа в дереве. Запись ${GetLeaf}(x_i, T_t, \sigma_0)$ означает следующее: используя перестановку $\sigma_0$ , мы выполняем target-кодирование обучающей выборки, и таким образом мы получаем значения всех признаков для примера . С помощью этих значений можно выбрать путь в дереве и определить номер листа. Таким образом, в строке 7 мы определяем номер листа для каждого обучающего примера, используя перестановку $\sigma_0$ . В итоге все обучающие примеры распределяются по листьям дерева .

В строке 8 мы рассчитываем градиент функции потерь по предсказаниями . Обозначение ${grad}_0(i)$ означает градиент по -му примеру. Индекс 0 здесь означает, что градиенты рассчитаны по . Далее для каждого листа дерева мы рассчитываем значение на этом листе, усредняя градиенты (со знаком минус) всех примеров, попавших в каждый лист. Далее (строка 12) мы обновляем , добавляя в него предсказания из нового дерева. В выражении $b^t_{{leaf}_0(i)}$ нижним индексом является номер листа для -го примера, соответственно все выражение означает значение, предсказываемое на -м примере, используя значения на листьях дерева .

В итоге, результатом шага является дерево со значениями на листьях. Также на каждом шаге обновляется массив , который используется в следующих шагах, и после обучения отбрасывается.

Алгоритм инференса CatBoost показан в строке 13. Мы суммируем предсказания по всем деревьям (с множителем $\alpha$ , как и при обучении). Чтобы получить предсказание для тестового примера, нужно выполнить target-кодирование на его категориальных признаках, для этого используется статистика, рассчитанная по всем обучающим примерам (что означает символ , подставленный вместо перестановки). Запись $b_j^t \mathbb{1}_{{GetLeaf}(x, T_t, {ApplyMode})=j}$ судя по всему означает то же самое, что $b^t_{{GetLeaf}(x, T_t, {ApplyMode})}$ , но записанное в виде скалярного произведения.

Теперь рассмотрим функцию . Эта функция принимает на вход обучающую выборку, массив промежуточных предсказаний (кроме ), массив перестановок (кроме $\sigma_0$ ), функцию потерь и коэффициент $\alpha$ . Функция возвращает новое дерево и обновленный массив промежуточных предсказаний.

В функции выбираем случайную перестановку $\sigma_r$ и далее работаем только с ней. Этой перестановке соответствует массив предсказаний , который имеет размерность $\lceil \log_2 n \rceil \times n$ . По этому массиву мы рассчитываем градиент ${grad}_r$ , который имеет такую же размерность.

Второй индекс () массива M соответствует порядку в упорядоченном бустинге. Каждому -му примеру из обучающей выборки можно сопоставить значение $\lfloor \log_2(\sigma_r(i)-1) \rfloor$ по этому индексу. В приведенной выше аналогии с мешками это номер мешка, в который попадает -й пример.

Массив (строка 3) имеет размерность (для задачи регрессии) и содержит производные для всех примеров обучающей выборки, то есть целевые данные для обучения следующего дерева. При этом производные по каждому примеру рассчитаны с помощью "виртуальной модели", ответственной за этот пример (вспомним, что модель, обучающаяся на первых мешках, используется для рассчета производных на -м мешке).

На каждом шаге роста дерева мы перебираем все возможные разделяющие правила (строка 6), то есть признаки и пороги разделения. Зафиксировав , мы хотим оценить качество, с которым полученное дерево предсказывает градиент . Для этого мы определяем листья, в которые попали примеры из обучающей выборки, используя перестановку $\sigma_r$ для target-кодирования (строка 8). Далее нужно определить значения на каждом листе, но делается это нетривиальным образом (строка 10). Глобальные, общие для всей выборки значения на листьях не рассчитываются. Вместо этого для -го обучающего примера предсказанием $\Delta(i)$ считается среднее значение градиента по всем примерам , попавшим в этот же лист ( ${leaf}_r(p)={leaf}_r(i)$ ) и имеющим меньший индекс в выбранной перестановке ( $\sigma_r(p) < \sigma_r(i)$ ). При этом глобальные значения на листьях дерева будут рассчитаны уже тогда, когда дерево будет полностью построено (строка 10 в алгоритме CatBoost).

Далее качество предсказания $\Delta(i)$ оценивается с помощью cosine similarity между ним и (строка 11), и на основании качества выбирается наилучшее решающее правило.

После того, как дерево построено, требуется обновить все промежуточные предсказания (строки 13-17), добавив слагаемое, предсказанное деревом на текущей итерации. Здесь в целом все аналогично.

Комбинирование признаков в CatBoost

Еще одной интересной особенностью CatBoost является комбинирование признаков при поиске оптимальных разделяющих правил. Ранее мы уже говорили о том, что категориальные признаки могут влиять на ответ не независимо друг от друга, и при target-кодировании эта информация будет утеряна (см. раздел "Работа с категориальными признаками"). Чтобы уменьшить влияние этой проблемы, в CatBoost применяется следующая стратегия (см. Dorogush et al, 2018, раздел "Feature combinations").

Пусть мы уже построили уровней дерева, использовав для разделения признаки $K_1, \dots, K_n$ , и на -м уровне рассматриваем возможность деления по некоему категориальному признаку . Мы комбинируем признак с признаками $K_1, \dots, K_n$ , то есть в качестве значений нового (комбинированного) признака рассматриваем все возможные сочетания значений признаков $K, K_1, \dots, K_n$ , и работаем с полученным признаком.

Впрочем, в статье этот механизм описан очень кратко, из-за чего остается не до конца понятным, как конкретно он реализован. В библиотеке CatBoost за комбинирование признаков отвечает параметр max_ctr_complexity.

Обзор некоторых параметров CatBoost

Выше мы рассмотрели алгоритм в том виде, в каком он приведен в научной статье. Программная реализация отличается тем, что в ней больше возможностей и гиперпараметров. Важно упомянуть, что CatBoost может использовать для обучения как CPU, так и GPU (параметр task_type метода fit). Многие значения гиперпараметры доступны либо только для CPU, либо только для GPU, из-за этого результаты обучения и метрика качества может отличаться.

Параметр grow_policy определяет тип деревьев и может принимать следующие значения:

grow_policy=SymmetricTree (по умолчанию) - использование решающих таблиц: одинаковая глубина всех листьев, общее разделяющее правило на каждом уровне дерева
grow_policy=Depthwise - одинаковая глубина всех листьев, но разделяющие правила могут быть разными в разных ветвях
grow_policy=Lossguide - обычное решающее дерево, глубина листьев могут быть разной

Параметр boosting_type задает тип бустинга: упорядоченный или неупорядоченный. Согласно документации, упорядоченный бустинг обучается медленнее, но обычно показывает лучшее качество на небольших датасетах. На CPU значение по умолчанию boosting_type='Plain', а на GPU значение по умолчанию выбирается в зависимости от размера обучающего датасета: если в нем меньше 50 тысяч примеров, то используется boosting_type='Ordered', за исключением отдельных частных случаев (см. документацию).

Также в CatBoost используется bootstrap aggregation (параметр bootstrap_type, подробнее см. в документации). Он может быть релализован в разных вариантах, например следующих:

При построении каждого следующего дерева оно обучается не на всей обучающей выборке, а на случайной подвыборке (bootstrap_type='Bernoulli'). Такой способ мы рассматривали в разделе "Регуляризация градиентного бустинга". При этом не только накладывается регуляризации, но и обучение выполняется быстрее.
При построении каждого следующего дерева обучающим примерам присваиваются случайные веса (bootstrap_type='Bayesian'), и при поиске оптимального разделения в основном учитываются примеры с большими весами.

Для поиска оптимальных разделяющих правил в CatBoost, конечно, перебираются не все возможные значения порога, которых очень много для больших датасетов, а значения с некоторым шагом (как и в других библиотеках - XGBoost, LightGBM). Подробнее см. Dorogush et al, 2018, раздел "Dense numerical features".

CatBoost также может работать с текстовыми признаками (для этого неявно используется модель bag-of-words). Это позволяет создавать на основе CatBoost отличные бейзлайны для задач табличного ML, в которых есть тестовые признаки. В методе fit нужно не забывать указывать параметры cat_features и text_features, чтобы алгоритм мог распознать типы признаков и корректно с ними работать.

Интерпретация ансамблей решающих деревьев

Одно дерево небольшой глубины полностью интерпретируемо, то есть процесс принятия решения уже представлен в понятной человеку форме. При ансамблировании большого числа деревьев часть интерпретируемости теряется, но тем не менее ансамбль деревьев интерпретируем лучше, чем, скажем, нейронная сеть. Начнем с оценки важности признаков.

Оценка важности признаков в решающих деревьях

В машинном обучении важностью признака (feature importance) неформально называется степень влияния этого признака на целевой признак. Оценка важности признаков имеет несомненную практическую пользу. При правильном применении она помогает отсеять нерелевантные признаки и в целом лучше понять данные. Кроме того, если мы сумеем найти признаки с явно завышенной важностью, то так мы можем распознать переобучение модели и утечку данных (подробнее см. здесь).

Понятие "степени влияния признака на ответ модели" можно формализовать по-разному.

Рассмотрим способ mean decrease impurity (MDI), который часто используется в решающих деревьях. В процессе построения решающего дерева добавление каждого решающего правила можно описать как шаг роста дерева, превращающий дерево $T_{\text{before}}$ в дерево $T_{\text{after}}$ (дерево $T_{\text{after}}$ имеет на один лист больше). Обозначим суммарную функцию потерь обоих деревьев за $\text{loss}(T_{\text{before}})$ и $\text{loss}(T_{\text{after}})$ . При этом новое решающее правило выбиралось таким образом, чтобы минимизировать $\text{loss}(T_{\text{after}})$ (см. раздел "Построение решающего дерева").

Мы можем посчитать падение функции потерь от добавления правила: $\text{loss}(T_{\text{after}}) - \text{loss}(T_{\text{before}})$ , и считать полученное значение важностью этого правила. Далее можно найти все правила во всех деревьях, использующих данный признак, и взять сумму важности эти правил по каждому дереву и среднее по всем деревьям.

Рассмотрим частный случай, когда функцией потерь является среднеквадратичная ошибка. Если до разделения на листе было значение , а после разделения появилось два листа со значениями и (см. раздел "Оптимальное разделение в задаче регрессии"), и количество примеров в листьях равно и , то получим следующую формулу для важности данного правила:

Такой способ расчета используется, например, в CatBoost (см. PredictionValuesChange).

Другой способ оценки важности некоего признака, называемый permutation importance, заключается в следующем: мы измеряем точность предсказания ансамбля деревьев на тестовой выборке, затем случайным образом переставляем значения этого признака и снова измеряем точность предсказания. Падение точности после перестановки и принимается за важность признака.

В оценке важности признаков таким способом кроется много подводных камней. Например, признак присутствует лишь в небольшой доле объектов, но сильно влияет на результат, тогда как признак оказывает лишь небольшое влияние на результат, но во всех объектах. Оба этих признака важны, но эта важность разного рода, и в стандартных методах оценки важности признаков не будет видно этого различия.

Более того, важность пропорциональна доле связанных с ним объектов в выборке, а эта доля может варьироваться в зависимости от способа сбора данных. Иными словами, важность признаков может сильно зависеть от особенностей распределения данных, а это распределение может отличаться при обучении и инференсе. Эта особенность добавляет неоднозначности понятию важности признака.

Переобученная модель может давать в целом неверную важность признаков. Если релевантность признаков заранее известна, то это может помочь распознать переобучение, но если релевантность заранее неизвестна, то отбор признаков на основе важности может в этом случае только усилить переобучение.

SHAP values

Еще одним, более современным способом оценки важности признаков являются SHAP values, основанные на теории игр. SHAP values позволяют оценить важность признаков на конкретном тестовом примере. SHAP values имеют некоторые проблемы. SHAP values, как и mean decrease impurity, зависит от распределения данных, то есть является характеристикой не только модели, но объединенной системы "модель + распределение данных". При этом можно получить ненулевые SHAP values для тех признаков, которые никак не используются моделью.

Перед использованием SHAP values полезно подробно ознакомиться с принципом работы этого метода, его преимуществами и недостатками. Подробнее см. в обзоре Интерпретация моделей и диагностика сдвига данных: LIME, SHAP и Shapley Flow.

Выразительная способность ансамблей решающих деревьев

Понятие выразительной способности

Любая модель машинного обучения - это некое параметризованное семейство функций $M = \{f_\theta|\theta \in \Theta\}$ . При обучении, как правило, мы выбираем одну из этих функций, которая хорошо приближает исследуемую зависимость $x \to y$ . Под выразительной способностью (expressivity) модели машинного обучения понимается то, насколько широкий класс функций представляет собой модель . Таким образом модели можно сравнивать друг с другом: модель имеет большую выразительную способность, чем модель , если $M_1 \supsetneq M_2$ . При этом функции в и могут быть параметризованы по разному.

Даже если какая-то функция отсутствует в модели , то возможно в найдутся функции, близкие к - это называется аппроксимацией функции моделью . Модель называется универсальным аппроксиматором, если с ее помощью можно со сколь угодно высокой точностью аппроксимировать любую функцию из достаточно широкого класса (например, любую непрерывную функцию или любую интегрируемую функцию; пример математически строгой формулировки см., например, здесь).

Прежде, чем переходить к решающим деревьям, вспомним нейронные сети. Нейронная сеть с одним скрытым слоем без функции активации имеет ту же выразительную способность, что и нейронная сеть без скрытых слоев (если размерность скрытого слоя не меньше, чем размерность входа и выхода). То есть эти модели равны как семейство функций, хотя параметризованы по-разному. Нейронная сеть с одним скрытым слоем и многими неполиномиальными функциями активации (например, ReLU или tanh) имеет выразительную способность намного больше, чем сеть без скрытых слоев, и при этом является универсальным аппроксиматором. Например, если мы используем функцию активации ReLU, то при конечном размере скрытого слоя не существует таких весов сети, чтобы сеть в точности реализовывала функцию , но подбирая веса и размер скрытого слоя можно создать сколь угодно точное приближение для этой функции на любом конечном интервале .

Если модель является универсальным аппроксиматором - это хорошо или плохо? Вопрос неоднозначный. Наличие факта универсальной аппроксимации ничего не говорит об обобщающей способности алгоритма, который будет осуществлять поиск решения. С одной стороны, отсутствие универсальной аппроксимации в модели может привести к тому, что обучиться некоторым типам зависимостей модель в принципе не способна. С другой стороны, наличие универсальной аппроксимации означает очень широкое пространство поиска и потенциальную возможность переобучиться на любом шуме (это будет еще зависеть от алгоритма обучения).

Итак, являются ли решающие деревья универсальными аппроксиматорами?

Выразительная способность решающего дерева

Решающие деревья (в том числе решающие таблицы, используемые в CatBoost), является универсальными аппроксиматорами при условии неограниченной глубины. С помощью дерева неограниченной глубины пространство можно разбить на сколь угодно маленькие участки, введя на каждом участке константное значение . Такое приближение напоминает сумму Римана (см. также Royden and Fitzpatrick "Real Analysis", The Simple Approximation Theorem).

Однако на практике глубину деревьев часто ограничивают, и более интересным является вопрос о том, являются ли универсальными аппроксиматорами ансамбли решающих деревьев ограниченной глубины. Я не смог найти в научной литературе исследования вопроса о том, являются ли ансамбли деревьев ограниченной глубины универсальными аппроксиматорами.

В этом разделе я приведу собственное доказательство того, что ансамбль деревьев фиксированной глубины не является универсальным аппроксиматором и способен аппроксимировать с произвольной точностью лишь те функции, которые представимы в виде суммы функций от признаков. Например, функция $f(x) = x_1 x_2 \dots x_{N+1}$ не может быть аппроксимирована с произвольной точностью ансамблем деревьев глубины .

Выразительная способность ансамбля решающих деревьев

Рассмотрим сначала ансамбль (т. е. сумму) деревьев, в котором все деревья имеют глубину 1, затем ансамбль деревьев глубины 2, и затем случай произвольной глубины .

Ансамбль деревьев глубины 1

При глубине 1 каждое дерево состоит из одного решающего правила и двух листьев. Каждое такое дерево может быть представлено как кусочно-постоянная функция от одного признака: $f(x) = (c_1 \text{ if } x{>}t \text{ else } c_2)$ . Сгруппировав все деревья в ансамбле по номеру признака, можно записать ансамбль в таком виде:

$f(x) = \sum\limits_i f_i(x_i) \tag{2}$

Здесь - любые кусочно-постоянные функции, представимые как сумма функцией вида $c_1 \text{ if } x{>}t \text{ else } c_2$ .

Отсюда, ансамблем деревьев глубины 1 можно представить любую функцию, представимую в виде , где - любая функция из очень широкого класса (интегрируемых по Риману) функций, которые можно сколь угодно точно приблизить кусочно-постоянной функцией.

Таким образом, с помощью ансамбля деревьев глубины 1 можно сколь угодно точно приблизить любую функцию, в которой зависимость представима в форме , где - произвольные функции. Если предсказывать не само значение , а его экспоненту, тогда суммирование в можно заменить произведением.

Ансамбль деревьев глубины 2

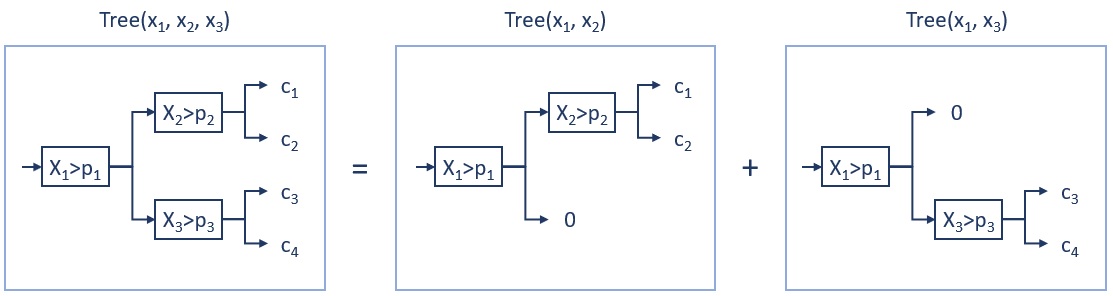
Дерево глубины 2 может иметь до трех решающих правил, а значит быть функцией от трех признаков. Однако такое дерево можно представить как сумму двух деревьев, в каждом из которых проверяется лишь два признака (рис. 7). Поэтому ансамбль из деревьев глубины 2 можно представить в виде суммы функций, каждая из которых использует 1 или 2 признака.

Рис. 7. Дерево глубины 2, использующее три признака, раскладывается в сумму двух деревьев, использующих по два признака.

Если ансамбль решающих деревьев как функцию можно разложить на слагаемые, каждое из которых использует по два признака, то такой ансамбль можно представить в виде функции:

$f(x) = \sum\limits_{i, j} f_{i, j}(x_i, x_j) \tag{3}$

При этом любую функцию от двух переменных можно аппроксимировать суммой деревьев глубины 2. Доказать это можно следующим образом: любую функцию (из очень широкого класса) можно сколь угодно точно аппроксимировать "кирпичиками" вида: $(c \text{ if } x_1{<}x{<}x_2 \text{ and } y_1{<}y{<}y_2)$ , и такой "кирпичик" можно построить, используя не более четырех деревьев глубины 2:

${Tree}_1: c \text{ if } \big( x{>}x_1 \text{ and } y{>}y_1 \big) \text{ else } 0$
${Tree}_2: -c \text{ if } \big( x{>}x_2 \text{ and } y{>}y_1 \big) \text{ else } 0$
${Tree}_3: -c \text{ if } \big( x{>}x_1 \text{ and } y{>}y_2 \big) \text{ else } 0$
${Tree}_4: c \text{ if } \big( x{>}x_2 \text{ and } y{>}y_2 \big) \text{ else } 0$

Отсюда можно сделать вывод о том, ансамблем решающих деревьев можно сколь угодно близко приблизить любую (интегрируемую по Риману) функцию, представимую в виде , где $f_{i, j}$ могут быть любыми.

Ансамбль деревьев глубины

Докажем, что ни при каком фиксированном ансамбль деревьев глубины не является универсальным аппроксиматором. Для этого достаточно показать, что произведение входных признаков не может быть сколь угодно точно аппроксимировано суммой деревьев глубины .

Введем запись $f \overset{\large{\epsilon}}{\approx} g$ , которая означает, что $\max |f(x) - g(x)| < \epsilon$ . По умолчанию будем считать, что области определения функций равны и максимум берется по всей области определения. Будем говорить, что функции из множества «сколь угодно точно аппроксимируют» функцию , если для любого $\epsilon > 0$ существует такое $a \in A$ , что $a \overset{\large{\epsilon}}{\approx} F$ . Иначе говоря, это означает, что существует последовательность функций из , равномерно сходящаяся к . Для упрощения в дальнейшем будем считать, что все переменные принимают значения в замкнутом промежутке . Введем также следующие обозначения:

- множество всех функций, представимых в виде суммы конечного числа решающих деревьев глубины .
- множество всех функций, представимых в виде суммы конечного числа функций от переменных.

Покажем, что $T_N \subset A_N$ . Каждое решающее дерево глубины можно представить как сумму деревьев, в которых лишь один лист содержит ненулевое значение, а значит решающее дерево глубины можно представить как сумму функций от переменных (для случая см. рис. 7).

Таким образом, осталось доказать, что функциями из множества нельзя сколь угодно точно аппроксимировать функцию $F(x) = x_1 x_2 \dots x_{N+1}$ . Чтобы упростить математическую нотацию, докажем для случая . Полученное доказательство обобщается на случай произвольного .

Теорема. Функцию нельзя сколь угодно точно аппроксимировать функциями из множества (а следовательно и функциями из множества ).

Доказательство. Докажем от противного. Зафиксируем произвольное $\epsilon$ . Пусть существует искомая аппроксимация:

$f_1(x_2,x_3,x_4)+f_2(x_1,x_3,x_4)+f_3(x_1,x_2,x_4)+f_4(x_1,x_2,x_3) \overset{\large{\epsilon}}{\approx} x_1 x_2 x_3 x_4$

Рассмотрим случаи и :

$x_4=0: \quad f_1(x_2,x_3,0)+f_2(x_1,x_3,0)+f_3(x_1,x_2,0)+f_4(x_1,x_2,x_3) \overset{\large{\epsilon}}{\approx} 0$

$x_4=1: \quad f_1(x_2,x_3,1)+f_2(x_1,x_3,1)+f_3(x_1,x_2,1)+f_4(x_1,x_2,x_3) \overset{\large{\epsilon}}{\approx} x_1 x_2 x_3$

Вычтем второе выражение из первого, при этом последнее слагаемое сократится:

$\underbrace{f_1(x_2,x_3,1)-f_1(x_2,x_3,0)}_{\large{g_1(x_2,x_3)}}+\underbrace{f_2(x_1,x_3,1)-f_2(x_1,x_3,0)}_{\large{g_2(x_1,x_3)}} \\ +\underbrace{f_3(x_1,x_2,1)-f_3(x_1,x_2,0)}_{\large{g_3(x_1,x_2)}} \overset{\large{2 \epsilon}}{\approx} x_1 x_2 x_3$

Мы пришли к тому, что функцию можно сколь угодно точно аппроксимировать сумой функций от двух переменных. Говоря более формально, имея ряд функций из , равномерно сходящийся к функции , можно построить ряд функций из , равномерно сходящийся к функции .

Повторив такой шаг, придем к тому, что функцию можно сколь угодно точно аппроксимировать сумой функций от одной переменной. Еще раз повторив такой шаг, придем к тому, что функцию можно сколь угодно точно аппроксимировать константой, что очевидно неверно. ■

Выводы и эксперименты

Как мы выяснили, суммой решающих деревьев ограниченной глубины нельзя аппроксимировать некоторые типы функций. Однако это не означает, что модель не сможет обучиться на конечной выборке, взятой из аргументов и значений таких функций. Просто такое обучение будет сопряжено с сильным переобучением.

Например, ансамбль деревьев глубины 1 не может аппроксимировать с произвольной точностью функцию . Возьмем выборку из 4 значений аргумента: . Поскольку ансамбль деревьев глубины 1 всегда можно представить как сумму функций от одной переменной (см. формулу ), то для любого ансамбля из деревьев глубины 1 будет верно следующее:

При этом для функции это равенство не выполняется, поэтому обучая ансамбль деревьев глубины 1 мы всегда будем видеть высокое значение функции потерь. Но если к исходным признакам добавить случайный шум, тогда, наоборот, функция потерь на обучающей выборке может стремиться к нулю, но получаемое решение будет некорректным и не будет обобщаться на тестовую выборку.

В качестве эксперимента попробуем обучить модель градиентного бустинга аппроксимировать функции и $x_1{+}x_2$ , с помощью обучающей выборки 256 точек, при этом точки могут быть распределены либо случайно, либюо по равномерной сетке. Будем использовать 1000 деревьев глубиной 1 или 2. Результаты эксперимента показаны на рис. 8. Каждое изображение представляет собой функцию , реализуемую обученной моделью.

Рис. 7. Аппроксимация градиентным бустингом функций x_1 + x_2 и x_1 x_2.

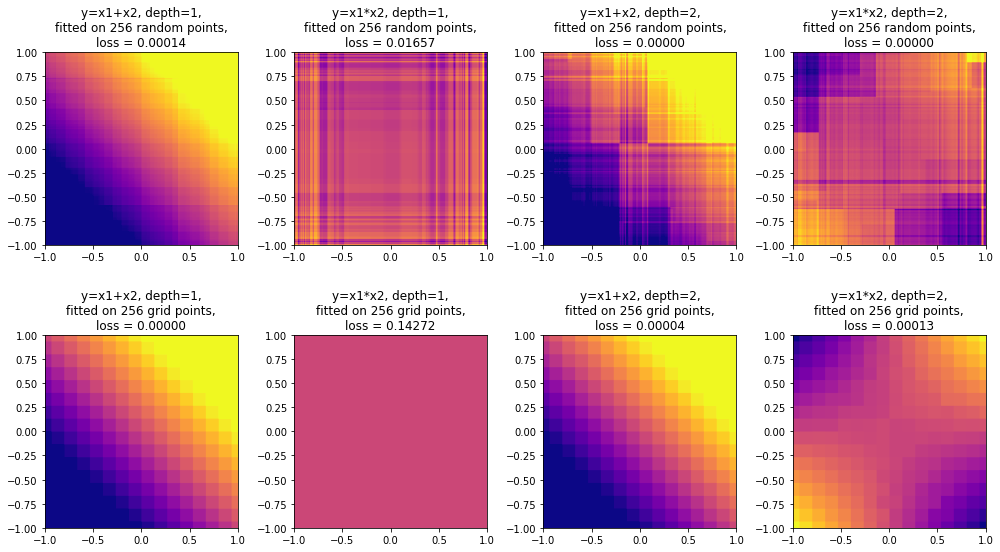
Как можно видеть, ансамбль деревьев глубины 1 может обучиться функции $x_1{+}x_2$ , но не может обучиться функции (второй столбец): при равномерном расположении точек обучения вообще не происходит, а при случайном расположении точек происходит лишь переобучение. Ансамбль деревьев глубины 2 при этом без труда обучается функции (четвертый столбец).

Что интересно, деревья глубины 1 лучше обучаются функции $x_1{+}x_2$ на случайных точках, чем деревья глубины 2. По-видимому, маленькую глубину дерева можно рассматривать как способ регуляризации, если известно, что искомая зависимость достаточно проста, например, имеет вид или .

Такие выводы, судя по всему, обобщаются и на случай большей размерности. В машинном обучении могут встречаться датасеты, где искомая зависимость имеет сложный вид и не представима как сумма функций от небольшого числа переменных. При этом библиотеки градиентного бустинга, такие как CatBoost, по умолчанию имеют не очень большую глубину дерева, из-за чего модель не сможет обучиться такой зависимости (недообучится либо переобучится, в зависимости от степени регуляризации).

Например, положительный ответ о выдаче кредита можно давать лишь тогда, когда одновременно строго соблюдено много условий. Если каждое условие представлено в виде бинарного признака, то искомая зависимость может иметь вид произведения многих признаков $x_1 x_2 \dots x_n$ . Хотя, с другой стороны, подобную зависимость можно описать в другом виде: $x_1 + x_2 + \dots + x_n > N$ . Поэтому вопрос о том, является ли отсутствие возможности универсальной аппроксимации существенным ограничением, остается открытым. Вполне возможно, что практически все зависимости на табличных данных, которые встречаются на практике, могут быть представлены как сумма функций от небольшого числа переменных.

Список источников

Biau et al., 2008. Consistency of Random Forests and Other Averaging Classifiers.
Breiman, 2001. Random Forests.
Chen and Guestrin, 2016. XGBoost: A Scalable Tree Boosting System.
Criminisi et al., 2011. Decision forests: A unified framework for classification, regression, density estimation, manifold learning and semi-supervised learning.
Dorogush et al., 2018. CatBoost: gradient boosting with categorical features support.
Freund and Schapire, 1997. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting.
Friedman, 2001. Greedy Function Approximation: A Gradient Boosting Machine.
Hancock et al., 1996. Lower Bounds on Learning Decision Lists and Trees.
Hyafil and Rivest, 1976. Constructing optimal binary decision trees is NP-complete.
Ke et al., 2017. LightGBM: A Highly Efficient Gradient Boosting Decision Tree.
Kohavi, 1994. Bottom-Up Induction of Oblivious Read-Once Decision Graphs.
Lundberg et al., 2019. Explainable AI for Trees: From Local Explanations to Global Understanding.
Modrý and Ferov, 2016. Enhancing LambdaMART Using Oblivious Trees.
Morgan and Sonquist, 1963. Problems in the Analysis of Survey Data, and a Proposal.
Pargent et al., 2021. Regularized target encoding outperforms traditional methods in supervised machine learning with high cardinality features.
Prokhorenkova et al., 2017. CatBoost: unbiased boosting with categorical features.
Rokach and Maimon, 2005. Decision Trees.
Royden and Fitzpatrick. Real Analysis.
Weinberger, 2018. Lecture 12: Bias-Variance Tradeoff.
Соколов, 2018. Решающие деревья.

Tags:

Hubs: