Содержание:
Вы наверняка скажете: «Аналитический градиент довольно прост, если брать производную для ваших простых выражений. Но это бесполезно. Что я буду делать, когда выражения станут намного больше? Разве уравнения не станут огромными и сложными довольно быстро?». Хороший вопрос. Да, выражения становятся намного сложнее. Но нет, это не делает все значительно труднее.
Как мы увидим далее, каждый логический элемент будет существовать сам по себе, абсолютно не подозревая о нюансах огромной и сложной схемы, частью которой он является. Он будет беспокоиться только о своих исходных значениях, и будет вычислять свои локальные производные так же, как описано в предыдущем разделе, за исключением того, что здесь будет одно дополнительное умножение, которое ему нужно будет выполнить.
Наверное, хватит нахваливать его. Надеюсь, я возбудил ваш интерес. Давайте углубимся в детали и включим в наш следующий пример два логических элемента:
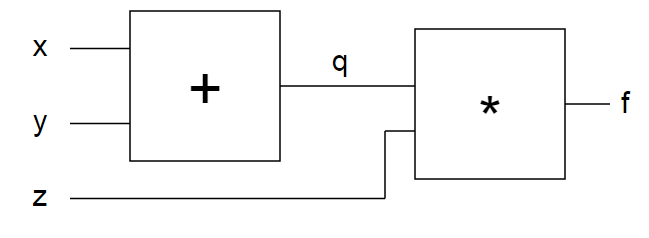
Выражение, которое мы вычисляем в данный момент, выглядит следующим образом: f(x,y,z)=(x+y)z. Давайте сформируем структуру кода, чтобы представить логические элементы в виде функций:
В вышеприведенном примере я использую a и b в качестве локальных переменных в функциях логических элементов. Таким образом, мы не будем путать их с исходными значениями схемы x,y,z. Как и раньше, мы заинтересованы в поиске производных по отношению к этим трем исходным значениям: x,y,z. Но как мы будем рассчитывать их теперь, когда у нас есть несколько логических элементов?
Для начала, давайте притворимся, что элемента + тут нет, и что у нас есть только две переменные в схеме: q,z и один логический элемент *. Обратите внимание, что q является результирующим значением логического элемента +. Если нам не надо беспокоиться об x и y, а только о q и z, тогда мы возвращаемся только к одному логическому элементу, так как задействован только элемент *, и мы знаем, что такое (аналитические) производные из предыдущего раздела. Мы можем записать их (при этом, заменяя x,y на q,z) следующим образом:
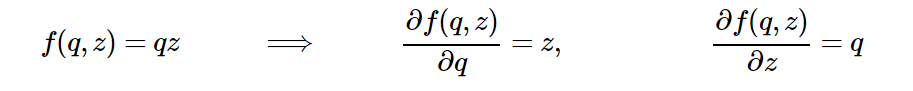
Все достаточно просто: это выражения градиента по отношению к q и z. Но стойте, нам не нужен градиент по отношению к q, а только по отношению к исходным значениям: x и y. К счастью, q вычисляется как функция x и y (путем прибавления в нашем примере). Мы можем записать градиент для логического элемента прибавления таким же образом, даже проще:
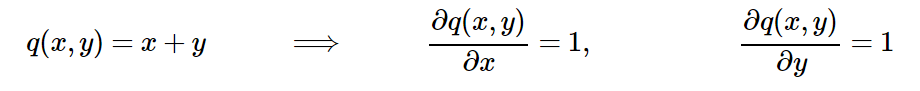
Все правильно, производные просто равны 1, вне зависимости от фактических значений x и y. Если вы задумались об этом, то это имеет смысл, так как чтобы сделать результат одного логического элемента сложения выше, нам нужно положительное изменение x и y, вне зависимости от их значений.
Обратное распространение ошибки
Мы, наконец, готовы воспользоваться Цепным правилом: мы знаем, как вычислять градиент q по отношению к x и y (это в случае одного логического элемента — +). И мы знаем, как вычислять градиент нашего конечного результата по отношению к q. Цепное правило рассказывает нам, как комбинировать эти подходы, чтобы получить градиент конечного результата по отношению к x и y, в котором мы, в конечном итоге, заинтересованы. Лучше всего то, что цепное правило просто утверждает, что правильнее всего – это взять и перемножить градиенты, чтобы связать их. Например, окончательной производной для x будет:
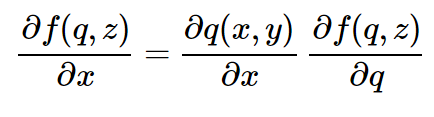
Здесь много символов, поэтому это опять же может показаться сложным, но это всего лишь два числа, перемножаемых между собой. Вот код:
Вот и все. Мы вычислили градиент и теперь можем позволить нашим исходным значениям немного реагировать на него. Давайте добавим градиенты в верхнюю часть исходных значений. Выходное значение схемы нужно сделать больше, чем -12!
Кажется, сработало! Давайте теперь попробуем интуитивно интерпретировать, что только что произошло. Схема хочет выдавать в результате более высокие значения. Последний логический элемент увидел исходные значения q = 3, z = -4 и вычислил результат -12. Путем «подталкивания» вверх, это выходное значение приложило силу на оба значения — q и z: чтобы увеличить выходное значение, схема «хочет», чтобы увеличилось значение z, как это видно из положительного значения производной (derivative_f_wrt_z = +3). Опять же, размер этой производной можно истолковать, как величину силы. С одной стороны, к q была приложена большая нисходящая сила, так как derivative_f_wrt_q = -4. Другими словами, схема хочет уменьшить q, приложив к нему силу равную 4.
Теперь мы подходим ко второму логическому элементу — "+", который выдает выходное значение q. По умолчанию, логический элемент + вычисляет свои производные, которые сообщают нам, как нужно изменить x и y, чтобы сделать q больше. НО! Вот важный момент: градиент значения q был вычислен как отрицательное число (derivative_f_wrt_q = -4), поэтому схема хочет уменьшить модуль q, прилагая силу, равную 4! Поэтому, если логический элемент + хочет помочь сделать окончательное выходное значение больше, он должен прислушиваться к сигналам градиента, поступающим сверху. В частности, в этом случае, он должен подтолкнуть x,y в противоположном направлении от того, куда он мог их подтолкнуть при нормальных условиях, и с силой, равной 4, если можно так выразиться. Умножение на -4, используемое в цепном правиле, приводит к следующему: вместо прикладывания положительной силы равной +1 на оба значения x и y (местную производную), полный градиент схемы по x и y становится равным 1 x -4 = -4. В этом есть смысл: схема хочет, чтобы x и y стали меньше, так как это приведет к уменьшению q, что, в свою очередь, приведет к увеличению f.
Давайте снова повторим то, что мы узнали:
В предыдущем разделе мы увидели, что в случае с одним логическим элементом (или одним выражением), мы можем взять производную аналитического градиента с помощью простого расчета. Мы интерпретировали градиент как силу или толчок на исходные значения, который толкает их в направлении, которое может сделать результат этого логического элемента выше.
В случае с несколькими логическими элементами, все остается примерно так же: каждый логический элемент существует самостоятельно, не подозревая о схеме, в которую он включен. Поступают некоторые исходные значения, и логический элемент вычисляет результат и производную по отношению к исходным значениям. Единственное различие на данном этапе заключается в том, что внезапно что-то может подтолкнуть этот логический элемент сверху. Это градиент окончательного выходного значения схемы по отношению к результату, который вычислил этот логический элемент. Именно схема запрашивает, чтобы логический элемент выдал в результате большее или меньшее число, прикладывая определенную силу. Логический элемент просто берет эту силу и умножает ее на все силы, которые он вычислил до этого для своих исходных значений (цепное правило). Это привело к желаемым результатам:
1. Если на логический элемент оказывается сильный положительный толчок сверху, он тоже сильнее толкает собственные исходные значения, дифференцированные по силе, приложенной на него сверху
2. А если на него оказывается отрицательный толчок, это означает, что схема хочет, чтобы его значение уменьшалось, а не увеличивалось, поэтому он приложит силу толчка на свои исходные значения, чтобы сделать собственное выходное значение меньше.
Разве это не прекрасно? Единственное различие между сценарием с одним логическим элементом и несколькими взаимодействующими логическими элементами, которые произвольно вычисляют сложные выражения, это дополнительная операция умножения, которая встречается в каждом логическом элементе.
Глава 1: Схемы реальных значений
Часть 1:
Часть 2:
Часть 3:
Часть 4:
Часть 5:
Часть 6:
Введение
Базовый сценарий: Простой логический элемент в схеме
Цель
Стратегия №1: Произвольный локальный поиск
Часть 2:
Стратегия №2: Числовой градиент
Часть 3:
Стратегия №3: Аналитический градиент
Часть 4:
Схемы с несколькими логическими элементами
Обратное распространение ошибки
Часть 5:
Шаблоны в «обратном» потоке
Пример "Один нейрон"
Часть 6:
Становимся мастером обратного распространения ошибки
Глава 2: Машинное обучение
Вы наверняка скажете: «Аналитический градиент довольно прост, если брать производную для ваших простых выражений. Но это бесполезно. Что я буду делать, когда выражения станут намного больше? Разве уравнения не станут огромными и сложными довольно быстро?». Хороший вопрос. Да, выражения становятся намного сложнее. Но нет, это не делает все значительно труднее.
Как мы увидим далее, каждый логический элемент будет существовать сам по себе, абсолютно не подозревая о нюансах огромной и сложной схемы, частью которой он является. Он будет беспокоиться только о своих исходных значениях, и будет вычислять свои локальные производные так же, как описано в предыдущем разделе, за исключением того, что здесь будет одно дополнительное умножение, которое ему нужно будет выполнить.
Одно дополнительное умножение превратит один (бесполезный) логический элемент в шестеренку в сложном механизме, который и представляет собой целую нейронную сеть.
Наверное, хватит нахваливать его. Надеюсь, я возбудил ваш интерес. Давайте углубимся в детали и включим в наш следующий пример два логических элемента:
Выражение, которое мы вычисляем в данный момент, выглядит следующим образом: f(x,y,z)=(x+y)z. Давайте сформируем структуру кода, чтобы представить логические элементы в виде функций:
var forwardMultiplyGate = function(a, b) {
return a * b;
};
var forwardAddGate = function(a, b) {
return a + b;
};
var forwardCircuit = function(x,y,z) {
var q = forwardAddGate(x, y);
var f = forwardMultiplyGate(q, z);
return f;
};
var x = -2, y = 5, z = -4;
var f = forwardCircuit(x, y, z); // результат равен -12
В вышеприведенном примере я использую a и b в качестве локальных переменных в функциях логических элементов. Таким образом, мы не будем путать их с исходными значениями схемы x,y,z. Как и раньше, мы заинтересованы в поиске производных по отношению к этим трем исходным значениям: x,y,z. Но как мы будем рассчитывать их теперь, когда у нас есть несколько логических элементов?
Для начала, давайте притворимся, что элемента + тут нет, и что у нас есть только две переменные в схеме: q,z и один логический элемент *. Обратите внимание, что q является результирующим значением логического элемента +. Если нам не надо беспокоиться об x и y, а только о q и z, тогда мы возвращаемся только к одному логическому элементу, так как задействован только элемент *, и мы знаем, что такое (аналитические) производные из предыдущего раздела. Мы можем записать их (при этом, заменяя x,y на q,z) следующим образом:
Все достаточно просто: это выражения градиента по отношению к q и z. Но стойте, нам не нужен градиент по отношению к q, а только по отношению к исходным значениям: x и y. К счастью, q вычисляется как функция x и y (путем прибавления в нашем примере). Мы можем записать градиент для логического элемента прибавления таким же образом, даже проще:
Все правильно, производные просто равны 1, вне зависимости от фактических значений x и y. Если вы задумались об этом, то это имеет смысл, так как чтобы сделать результат одного логического элемента сложения выше, нам нужно положительное изменение x и y, вне зависимости от их значений.
Обратное распространение ошибки
Мы, наконец, готовы воспользоваться Цепным правилом: мы знаем, как вычислять градиент q по отношению к x и y (это в случае одного логического элемента — +). И мы знаем, как вычислять градиент нашего конечного результата по отношению к q. Цепное правило рассказывает нам, как комбинировать эти подходы, чтобы получить градиент конечного результата по отношению к x и y, в котором мы, в конечном итоге, заинтересованы. Лучше всего то, что цепное правило просто утверждает, что правильнее всего – это взять и перемножить градиенты, чтобы связать их. Например, окончательной производной для x будет:
Здесь много символов, поэтому это опять же может показаться сложным, но это всего лишь два числа, перемножаемых между собой. Вот код:
// изначальные условия
var x = -2, y = 5, z = -4;
var q = forwardAddGate(x, y); // q равно 3
var f = forwardMultiplyGate(q, z); // результат равен -12
// градиент логического элемента УМНОЖЕНИЕ по отношению к его исходным значениям
// wrt – это сокращение «в отношении» ("with respect to")
var derivative_f_wrt_z = q; // 3
var derivative_f_wrt_q = z; // -4
// производная логического элемента сложение по отношению к его исходным значениям
var derivative_q_wrt_x = 1.0;
var derivative_q_wrt_y = 1.0;
// цепное правило
var derivative_f_wrt_x = derivative_q_wrt_x * derivative_f_wrt_q; // -4
var derivative_f_wrt_y = derivative_q_wrt_y * derivative_f_wrt_q; // -4
Вот и все. Мы вычислили градиент и теперь можем позволить нашим исходным значениям немного реагировать на него. Давайте добавим градиенты в верхнюю часть исходных значений. Выходное значение схемы нужно сделать больше, чем -12!
// конечный градиент, согласно вышеуказанному: [-4, -4, 3]
var gradient_f_wrt_xyz = [derivative_f_wrt_x, derivative_f_wrt_y, derivative_f_wrt_z]
// позволим исходным значениям реагировать на силу/толчок:
var step_size = 0.01;
x = x + step_size * derivative_f_wrt_x; // -2.04
y = y + step_size * derivative_f_wrt_y; // 4.96
z = z + step_size * derivative_f_wrt_z; // -3.97
// Наша схема теперь должна иметь более высокий результат:
var q = forwardAddGate(x, y); // q становится 2.92
var f = forwardMultiplyGate(q, z); // результат равен -11.59, больше, чем -12!
Кажется, сработало! Давайте теперь попробуем интуитивно интерпретировать, что только что произошло. Схема хочет выдавать в результате более высокие значения. Последний логический элемент увидел исходные значения q = 3, z = -4 и вычислил результат -12. Путем «подталкивания» вверх, это выходное значение приложило силу на оба значения — q и z: чтобы увеличить выходное значение, схема «хочет», чтобы увеличилось значение z, как это видно из положительного значения производной (derivative_f_wrt_z = +3). Опять же, размер этой производной можно истолковать, как величину силы. С одной стороны, к q была приложена большая нисходящая сила, так как derivative_f_wrt_q = -4. Другими словами, схема хочет уменьшить q, приложив к нему силу равную 4.
Теперь мы подходим ко второму логическому элементу — "+", который выдает выходное значение q. По умолчанию, логический элемент + вычисляет свои производные, которые сообщают нам, как нужно изменить x и y, чтобы сделать q больше. НО! Вот важный момент: градиент значения q был вычислен как отрицательное число (derivative_f_wrt_q = -4), поэтому схема хочет уменьшить модуль q, прилагая силу, равную 4! Поэтому, если логический элемент + хочет помочь сделать окончательное выходное значение больше, он должен прислушиваться к сигналам градиента, поступающим сверху. В частности, в этом случае, он должен подтолкнуть x,y в противоположном направлении от того, куда он мог их подтолкнуть при нормальных условиях, и с силой, равной 4, если можно так выразиться. Умножение на -4, используемое в цепном правиле, приводит к следующему: вместо прикладывания положительной силы равной +1 на оба значения x и y (местную производную), полный градиент схемы по x и y становится равным 1 x -4 = -4. В этом есть смысл: схема хочет, чтобы x и y стали меньше, так как это приведет к уменьшению q, что, в свою очередь, приведет к увеличению f.
Если для вас в этом есть смысл, значит, вы понимаете обратное распространение ошибки.
Давайте снова повторим то, что мы узнали:
В предыдущем разделе мы увидели, что в случае с одним логическим элементом (или одним выражением), мы можем взять производную аналитического градиента с помощью простого расчета. Мы интерпретировали градиент как силу или толчок на исходные значения, который толкает их в направлении, которое может сделать результат этого логического элемента выше.
В случае с несколькими логическими элементами, все остается примерно так же: каждый логический элемент существует самостоятельно, не подозревая о схеме, в которую он включен. Поступают некоторые исходные значения, и логический элемент вычисляет результат и производную по отношению к исходным значениям. Единственное различие на данном этапе заключается в том, что внезапно что-то может подтолкнуть этот логический элемент сверху. Это градиент окончательного выходного значения схемы по отношению к результату, который вычислил этот логический элемент. Именно схема запрашивает, чтобы логический элемент выдал в результате большее или меньшее число, прикладывая определенную силу. Логический элемент просто берет эту силу и умножает ее на все силы, которые он вычислил до этого для своих исходных значений (цепное правило). Это привело к желаемым результатам:
1. Если на логический элемент оказывается сильный положительный толчок сверху, он тоже сильнее толкает собственные исходные значения, дифференцированные по силе, приложенной на него сверху
2. А если на него оказывается отрицательный толчок, это означает, что схема хочет, чтобы его значение уменьшалось, а не увеличивалось, поэтому он приложит силу толчка на свои исходные значения, чтобы сделать собственное выходное значение меньше.
Неплохой пример, которую следует иметь в виду: мы толкаем результат схемы и это приводит к нисходящему толчку через всю схему вплоть до исходных значений.
Разве это не прекрасно? Единственное различие между сценарием с одним логическим элементом и несколькими взаимодействующими логическими элементами, которые произвольно вычисляют сложные выражения, это дополнительная операция умножения, которая встречается в каждом логическом элементе.