Итак, в прошлый раз мы немного поговорили о том, что такое вообще рекомендательные системы и какие перед ними стоят проблемы, а также о том, как выглядит постановка задачи коллаборативной фильтрации. Сегодня я расскажу об одном из самых простых и естественных методов коллаборативной фильтрации, с которого в 90-х годах и начались исследования в этой области. Базовая идея очень проста: как понять, понравится ли Васе фильм «Трактористы»? Нужно просто найти других пользователей, похожих на Васю, и посмотреть, какие рейтинги они ставили «Трактористам». Или с другой стороны: как понять, понравится ли фильм «Трактористы» Васе? Нужно просто найти другие фильмы, похожие на «Трактористов», и посмотреть, как Вася их оценивал.

Напомню, что у нас есть сильно разреженная матрица, состоящая из рейтингов (лайков, фактов покупки и т.п.), которые пользователи (строки матрицы) присвоили продуктам (столбцы матрицы):
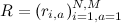
Наша задача – предсказывать оценки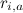 , зная некоторые уже расставленные в матрице оценки
, зная некоторые уже расставленные в матрице оценки 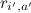 . Наше наилучшее предсказание будем обозначать через
. Наше наилучшее предсказание будем обозначать через 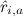 . Если мы сможем получить такие предсказания, нужно будет просто выбрать один или несколько продуктов, для которых
. Если мы сможем получить такие предсказания, нужно будет просто выбрать один или несколько продуктов, для которых 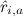 максимальны.
максимальны.
Мы упомянули два подхода: либо искать похожих пользователей – это называется «рекомендации, основанные на пользователях» (user-based collaborative filtering), либо искать похожие продукты – это, что логично, называется «рекомендации, основанные на продуктах» (item-based collaborative filtering). Собственно, основной алгоритм в обоих случаях понятен.
Осталось только понять, как же всё это делать.
Во-первых, нужно определить, что значит «похожий». Напоминаю, что всё, что у нас есть – это вектор предпочтений для каждого пользователя (строки матрицы R) и вектор оценок пользователей для каждого продукта (столбцы матрицы R). Прежде всего оставим в этих векторах только те элементы, для которых нам известны значения в обоих векторах, т.е. оставим только те продукты, которые оценили оба пользователя, или только тех пользователей, которые оба оценили данный продукт. В результате нам просто нужно определить, насколько похожи два вектора вещественных чисел. Это, конечно, известная задача, и классическое её решение – подсчитать коэффициент корреляции: для двух векторов предпочтений пользователей i и j коэффициент корреляции Пирсона равен
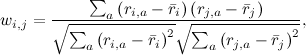
где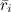 — средний рейтинг, выставленный пользователем i. Иногда пользуются так называемой «косинусной похожестью», используя косинус угла между векторами:
— средний рейтинг, выставленный пользователем i. Иногда пользуются так называемой «косинусной похожестью», используя косинус угла между векторами:
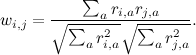
Но для того, чтобы косинус хорошо работал, желательно всё равно сначала вычесть среднее по каждому вектору, так что в реальности это та же самая метрика.
Для примера рассмотрим какую-нибудь матрицу оценок.

Ручной анализ предпочтений мы оставим читателю, а сами подсчитаем для user-based рекомендаций корреляцию между вектором предпочтений Васи и остальных участников системы.
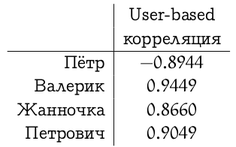
Мы сейчас привели формулы для user-based рекомендаций. В item-based подходе ситуация похожая, но есть один нюанс: разные пользователи по-разному относятся к оценкам, кто-то ставит всем подряд по пять звёздочек («лайкает» все подряд сайты), а кто-то, наоборот, ставит всем по две-три звёздочки (часто жмёт «дизлайк»). Для первого пользователя низкий рейтинг («дизлайк») будет гораздо более информативен, чем высокий, а для второго – наоборот. В user-based подходе об этом автоматически заботится коэффициент корреляции. А в item-based рекомендациях, чтобы это учесть, можно, например, вычесть из каждой оценки средний рейтинг того или иного пользователя, а потом уже подсчитать корреляцию или косинус угла между векторами. Тогда в формуле для косинуса получится
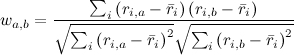 ,
,
где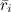 обозначает средний рейтинг, выставленный пользователем i. В нашем примере, если вычесть из каждого вектора оценок среднее, получится вот что:
обозначает средний рейтинг, выставленный пользователем i. В нашем примере, если вычесть из каждого вектора оценок среднее, получится вот что:
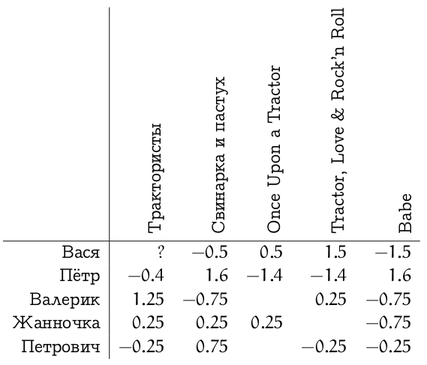
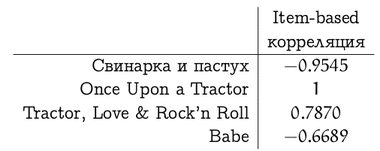
И тогда корреляция между вектором оценок фильма «Трактористы» и оценками других фильмов составит (заметим, что с «Once Upon a Tractor» сложилась вырожденная ситуация, потому что пересекающихся оценок было слишком мало)
У этих мер похожести есть свои недостатки и разнообразные вариации на тему, но давайте для иллюстрации методов ими ограничимся. Таким образом, мы разобрались с первым пунктом плана; на очереди второй – как воспользоваться этими оценками похожести (весами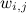 )?
)?
Простой и логичный подход – приблизить новый рейтинг как средний рейтинг данного пользователя плюс отклонения от среднего рейтингов других пользователей, взвешенных этими самыми весами:
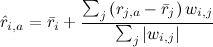 .
.
Этот подход иногда ещё называют GroupLens algorithm – так работал дедушка рекомендательных систем GroupLens (кстати, pardon the pun, рекомендую сайт MovieLens] – с него когда-то фактически начиналась серьёзная коллаборативная фильтрация, но и сегодня он может порадовать малоизвестными фильмами, которые вам понравятся). В случае с Васей и «Трактористами» по этому методу ожидается оценка около 3.9 (Петрович чуть подкачал), так что можно смело смотреть.
Для item-based рекомендаций всё совершенно эквивалентно – нужно просто найти взвешенное среднее уже оцененных пользователем продуктов:
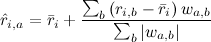
Item-based метод в нашем примере предполагает, что Вася поставит «Трактористам» аж 4.4.
Конечно, теоретически всё это хорошо, но в реальности вряд ли получится для каждой рекомендации суммировать данные от миллионов пользователей. Поэтому эту формулу обычно огрубляют до k ближайших соседей – k пользователей, максимально похожих на данного пользователя и уже оценивших этот продукт:
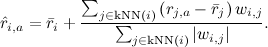
Остаётся только понять, как быстро искать ближайших соседей. Это уже выходит за рамки нашего обсуждения, поэтому я просто назову два основных метода: в небольших размерностях можно пользоваться k-d-деревьями (k-d-trees, см., например, это введение), а в больших размерностях выручит локально-чувствительное хеширование (locally sensitive hashing, см., например, здесь).
Итак, сегодня мы рассмотрели простейшие рекомендательные алгоритмы, которые оценивают похожесть пользователя (продукта) на других пользователей (другие продукты), а потом рекомендуют, исходя из мнения ближайших соседей по этой метрике. Не следует, кстати, думать, что эти методы окончательно устарели – для многих задач они прекрасно работают. Однако в следующих сериях мы перейдём к более тонкому анализу имеющейся информации. В частности, я с самого начала упорно называл входные данные «матрицей рейтингов», хотя, казалось бы, мы нигде не использовали то, что это действительно матрица, а не просто набор векторов (либо строк, либо столбцов, в зависимости от метода). В следующий раз – используем.
P.S. За картинки с формулами спасибо сервису mathURL. К сожалению, русские буквы он не понимает, поэтому таблицы про Васю и Петровича пришлось делать руками.

Напомню, что у нас есть сильно разреженная матрица, состоящая из рейтингов (лайков, фактов покупки и т.п.), которые пользователи (строки матрицы) присвоили продуктам (столбцы матрицы):

Наша задача – предсказывать оценки
 , зная некоторые уже расставленные в матрице оценки
, зная некоторые уже расставленные в матрице оценки  . Наше наилучшее предсказание будем обозначать через
. Наше наилучшее предсказание будем обозначать через 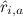 . Если мы сможем получить такие предсказания, нужно будет просто выбрать один или несколько продуктов, для которых
. Если мы сможем получить такие предсказания, нужно будет просто выбрать один или несколько продуктов, для которых 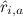 максимальны.
максимальны.Мы упомянули два подхода: либо искать похожих пользователей – это называется «рекомендации, основанные на пользователях» (user-based collaborative filtering), либо искать похожие продукты – это, что логично, называется «рекомендации, основанные на продуктах» (item-based collaborative filtering). Собственно, основной алгоритм в обоих случаях понятен.
- Найти, насколько другие пользователи (продукты) в базе данных похожи на данного пользователя (продукт).
- По оценкам других пользователей (продуктов) предсказать, какую оценку даст данный пользователь данному продукту, учитывая с большим весом тех пользователей (продукты), которые больше похожи на данный.
Осталось только понять, как же всё это делать.
Во-первых, нужно определить, что значит «похожий». Напоминаю, что всё, что у нас есть – это вектор предпочтений для каждого пользователя (строки матрицы R) и вектор оценок пользователей для каждого продукта (столбцы матрицы R). Прежде всего оставим в этих векторах только те элементы, для которых нам известны значения в обоих векторах, т.е. оставим только те продукты, которые оценили оба пользователя, или только тех пользователей, которые оба оценили данный продукт. В результате нам просто нужно определить, насколько похожи два вектора вещественных чисел. Это, конечно, известная задача, и классическое её решение – подсчитать коэффициент корреляции: для двух векторов предпочтений пользователей i и j коэффициент корреляции Пирсона равен
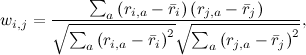
где
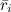 — средний рейтинг, выставленный пользователем i. Иногда пользуются так называемой «косинусной похожестью», используя косинус угла между векторами:
— средний рейтинг, выставленный пользователем i. Иногда пользуются так называемой «косинусной похожестью», используя косинус угла между векторами: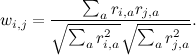
Но для того, чтобы косинус хорошо работал, желательно всё равно сначала вычесть среднее по каждому вектору, так что в реальности это та же самая метрика.
Для примера рассмотрим какую-нибудь матрицу оценок.

Ручной анализ предпочтений мы оставим читателю, а сами подсчитаем для user-based рекомендаций корреляцию между вектором предпочтений Васи и остальных участников системы.
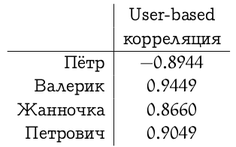
Мы сейчас привели формулы для user-based рекомендаций. В item-based подходе ситуация похожая, но есть один нюанс: разные пользователи по-разному относятся к оценкам, кто-то ставит всем подряд по пять звёздочек («лайкает» все подряд сайты), а кто-то, наоборот, ставит всем по две-три звёздочки (часто жмёт «дизлайк»). Для первого пользователя низкий рейтинг («дизлайк») будет гораздо более информативен, чем высокий, а для второго – наоборот. В user-based подходе об этом автоматически заботится коэффициент корреляции. А в item-based рекомендациях, чтобы это учесть, можно, например, вычесть из каждой оценки средний рейтинг того или иного пользователя, а потом уже подсчитать корреляцию или косинус угла между векторами. Тогда в формуле для косинуса получится
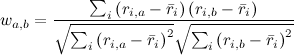 ,
,где
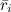 обозначает средний рейтинг, выставленный пользователем i. В нашем примере, если вычесть из каждого вектора оценок среднее, получится вот что:
обозначает средний рейтинг, выставленный пользователем i. В нашем примере, если вычесть из каждого вектора оценок среднее, получится вот что:
И тогда корреляция между вектором оценок фильма «Трактористы» и оценками других фильмов составит (заметим, что с «Once Upon a Tractor» сложилась вырожденная ситуация, потому что пересекающихся оценок было слишком мало)
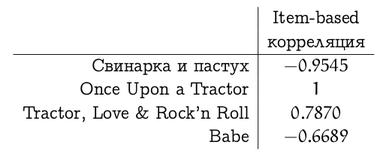
У этих мер похожести есть свои недостатки и разнообразные вариации на тему, но давайте для иллюстрации методов ими ограничимся. Таким образом, мы разобрались с первым пунктом плана; на очереди второй – как воспользоваться этими оценками похожести (весами
 )?
)?Простой и логичный подход – приблизить новый рейтинг как средний рейтинг данного пользователя плюс отклонения от среднего рейтингов других пользователей, взвешенных этими самыми весами:
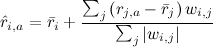 .
.Этот подход иногда ещё называют GroupLens algorithm – так работал дедушка рекомендательных систем GroupLens (кстати, pardon the pun, рекомендую сайт MovieLens] – с него когда-то фактически начиналась серьёзная коллаборативная фильтрация, но и сегодня он может порадовать малоизвестными фильмами, которые вам понравятся). В случае с Васей и «Трактористами» по этому методу ожидается оценка около 3.9 (Петрович чуть подкачал), так что можно смело смотреть.
Для item-based рекомендаций всё совершенно эквивалентно – нужно просто найти взвешенное среднее уже оцененных пользователем продуктов:

Item-based метод в нашем примере предполагает, что Вася поставит «Трактористам» аж 4.4.
Конечно, теоретически всё это хорошо, но в реальности вряд ли получится для каждой рекомендации суммировать данные от миллионов пользователей. Поэтому эту формулу обычно огрубляют до k ближайших соседей – k пользователей, максимально похожих на данного пользователя и уже оценивших этот продукт:
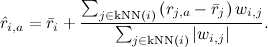
Остаётся только понять, как быстро искать ближайших соседей. Это уже выходит за рамки нашего обсуждения, поэтому я просто назову два основных метода: в небольших размерностях можно пользоваться k-d-деревьями (k-d-trees, см., например, это введение), а в больших размерностях выручит локально-чувствительное хеширование (locally sensitive hashing, см., например, здесь).
Итак, сегодня мы рассмотрели простейшие рекомендательные алгоритмы, которые оценивают похожесть пользователя (продукта) на других пользователей (другие продукты), а потом рекомендуют, исходя из мнения ближайших соседей по этой метрике. Не следует, кстати, думать, что эти методы окончательно устарели – для многих задач они прекрасно работают. Однако в следующих сериях мы перейдём к более тонкому анализу имеющейся информации. В частности, я с самого начала упорно называл входные данные «матрицей рейтингов», хотя, казалось бы, мы нигде не использовали то, что это действительно матрица, а не просто набор векторов (либо строк, либо столбцов, в зависимости от метода). В следующий раз – используем.
P.S. За картинки с формулами спасибо сервису mathURL. К сожалению, русские буквы он не понимает, поэтому таблицы про Васю и Петровича пришлось делать руками.