Кластеризация — это такая магическая штука: она превращает большой объём неструктурированных данных в потенциально обозримый набор кластеров, анализ которых позволяет делать выводы о содержании этих данных.
Приложений у методов кластеризации огромное количество. Например, мы кластеризуем поисковые запросы для того, чтобы повышать обобщающую способность алгоритмов ранжирования: любая статистика, вычисленная по группе похожих запросов, надёжнее той же статистики, вычисленной для одного отдельного запроса. Кластеризация позволяет повышать качество на запросах с редко встречающимися формулировками. Другой понятный пример — Яндекс.Новости, которые автоматически формируют сюжеты из новостных сообщений.
В далёком 2013 году мне повезло поучаствовать в разработке очень сложного алгоритма кластеризации. Требовалось с очень высоким качеством кластеризовать сотни тысяч объектов и делать это быстро: за десятки секунд на одной машине. Первым делом нужно было построить систему оценки качества, и в этой статье я расскажу именно о ней.
Когда речь заходит об оценке качества, начинать нужно, конечно же, с метрик.
Алгоритм кластеризации можно и нужно оценивать с позиции сервиса, частью которого этот алгоритм является: рост качества кластеризации должен приводить к росту числа пользователей, конверсий, возвращаемости и так далее, так что классическое А/Б-тестирование вполне уместно. Вместе с тем любой большой системе нужны метрики, специфичные для каждого из её компонентов. Кластеризация — не исключение.
1. Метрики и их свойства
Обычно задано образцовое разбиение на кластеры и разбиение, построенное алгоритмически. Метрика качества должна оценить степень соответствия между ними.
Обсуждение метрик стоит предварить обсуждением принципов, которым эти метрики должны удовлетворять. В статье Amigo et. al, 2009. A comparison of Extrinsic Clustering Evaluation Metrics based on Formal Constraints очень подробно разбирается ряд принципов, их корректность и то, как различные классы метрик удовлетворяют этим принципам.
1.1. Cluster Homogeneity, однородность кластеров

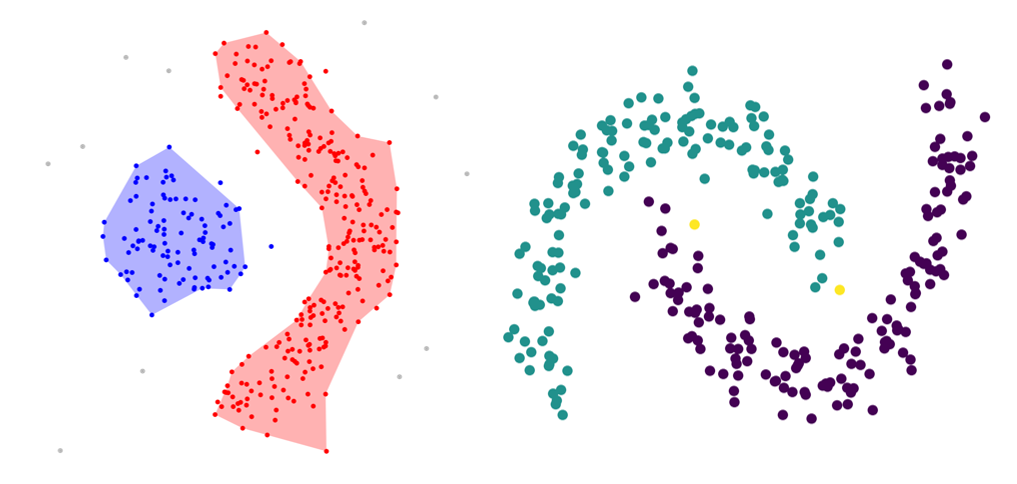
Значение метрики качества должно уменьшаться при объединении в один кластер двух эталонных.
1.2. Cluster Completeness, полнота кластеров
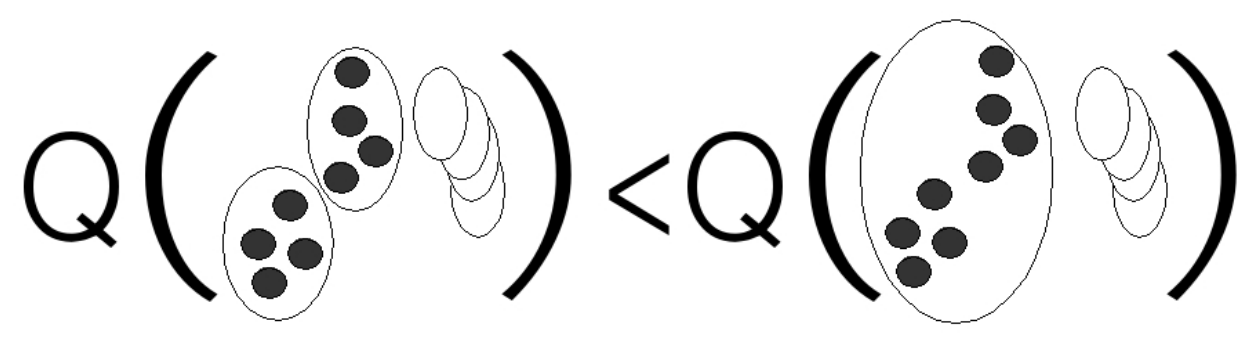
Это свойство, двойственное свойству однородности. Значение метрики качества должно уменьшаться при разделении эталонного кластера на части.
1.3. Rag Bag
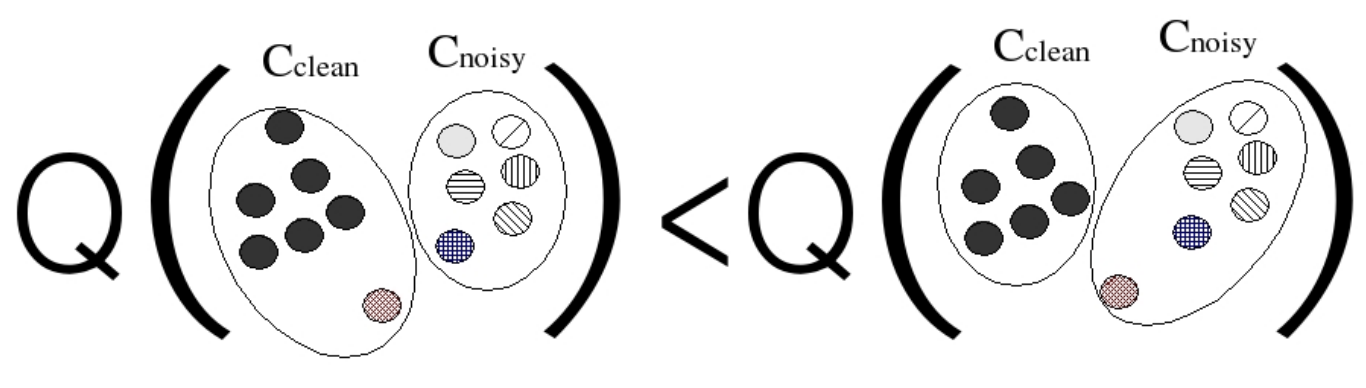
Пусть есть два кластера: чистый, содержащий элементы из одного эталонного кластера, и шумный («лоскутный»), где собраны элементы из большого числа различных эталонных кластеров. Тогда значение метрики качества должно быть выше у той версии кластеризации, которая помещает новый нерелевантный обоим кластерам элемент в шумный кластер, по сравнению с версией, которая помещает этот элемент в чистый кластер.
Это свойство может показаться очень естественным, но обязательно нужно принимать во внимание специфику приложения. Скажем, в Яндекс.Новостях большие «лоскутные» кластеры очень вредны: их невозможно адекватно проаннотировать, а благодаря своему размеру и разнообразию источников они могут ранжироваться очень высоко.
1.4. Size vs Quantity

Значительное ухудшение кластеризации большого числа небольших кластеров должно обходиться дороже небольшого ухудшения кластеризации в крупном кластере.
2. Метрики качества кластеризации
Теперь обсудим несколько важных классов метрик качества кластеризации.
Будем считать заданным конечное множество объектов . Множеством кластеров будем называть всякую совокупность его непересекающихся непустых подмножеств. Таким образом,
— множество кластеров, если
При этом множество кластеров не обязательно является покрытием множества объектов: допускается неполная кластеризация. Впрочем, иногда удобно считать каждый некластеризованный элемент тривиальным одноэлементным кластером.
Будем считать, что определены два множества кластеров: эталонное и построенное алгоритмом
. Через
и
будем обозначать, соответственно, эталонный и алгоритмический кластеры, которым принадлежит объект
.
2.1. Метрики, основанные на подсчёте пар (классификационные)
В этом подходе задача кластеризации сводится к бинарной классификации на множестве пар объектов. Пара объектов считается относящейся к положительному классу тогда и только тогда, когда оба объекта относятся к одному и тому же эталонному кластеру. Предсказание считается положительным тогда и только тогда, когда эти объекты относятся к одному и тому же алгоритмическому кластеру.
Иллюстрация ниже поясняет это определение. Восемь объектов разбиты на три эталонных кластера размеров 3 («жёлтый»), 3 («фиолетовый») и 2 («синий»). Эти же объекты кластеризованы алгоритмом так: «синий» кластер собран абсолютно верно, а вот один из «фиолетовых» объектов ошибочно отнесён в кластер к «жёлтым».

Тогда здесь суммарно пар объектов, из них:
— положительных;
— отрицательных.
Построенная алгоритмом матрица содержит шесть лишних положительных элементов за счёт создания связей между «жёлтыми» объектами и одним из «фиолетовых» объектов, а также теряет четыре элемента из-за потери связей между «фиолетовыми» элементами.
В терминах качества бинарной классификации получается, что:
— пар определены как положительные и при этом являются положительными;
— пар определены как положительные, но ими не являются;
— пар определены как отрицательные и при этом являются отрицательными;
— пары определены как отрицательные, но ими не являются.
Теперь можно вычислить точность, полноту и любые другие метрики:
В процессе вычислений можно учитывать тот факт, что матрица симметрична: это вносит изменения в получаемые значения.
Описанный способ интуитивно очень понятен и прост в реализации. Другая его замечательная особенность в том, что получение оценок не требует построения эталонного разбиения на кластеры: достаточно разметить репрезентативное множество пар объектов.
Главный недостаток pairwise-метрик — квадратичная зависимость числа порождаемых пар от размера кластера. Из-за этого значение pairwise-метрик может быть обусловлено качеством кластеризации буквально нескольких самых крупных кластеров.
2.2. Метрики, основанные на сопоставлении множеств
Для определения метрик этого класса вначале вводятся метрики точности и полноты соответствия между кластером и эталоном:
Пример ниже содержит два эталонных кластера: «жёлтый» (y) и «фиолетовый» (v). Единственный алгоритмический кластер содержит 25 жёлтых точек и 10 фиолетовых. Точность соответствия этого кластера жёлтому кластеру составляет 25/35, а фиолетовому — 10/35. Вне кластера находятся ещё пять жёлтых и две фиолетовых точки. Значит, всего имеется 30 жёлтых и 12 фиолетовых точек, поэтому полнота соответствия жёлтому кластеру равна 25/30, фиолетовому — 10/12.

Физический смысл введённых величин прост: точность равна вероятности выбрать элемент эталонного кластера при выборе случайного элемента из алгоритмического кластера, полнота равна вероятности выбрать элемент алгоритмического кластера при выборе случайного элемента из эталонного кластера. Показатели двойственны:
Далее можно определить и F-меру:
Теперь необходимо определить интегральный показатель. Самый известный способ определить его через показатели отдельных соответствий приводит к метрике «чистоты» кластеров, Purity:
Вводится и двойственная метрика, в которой суммирование и нормировка производятся по эталонным кластерам:
Высокое значение означает, что для кластера найдётся хорошо соответствующий ему эталон. Высокое значение
— что для эталона найдётся хорошо соответствующий ему алгоритмический кластер. Значит ли это, что близость обеих метрик к единице гарантирует очень хорошее качество кластеризации? К сожалению, нет. Рассмотрим следующий пример:
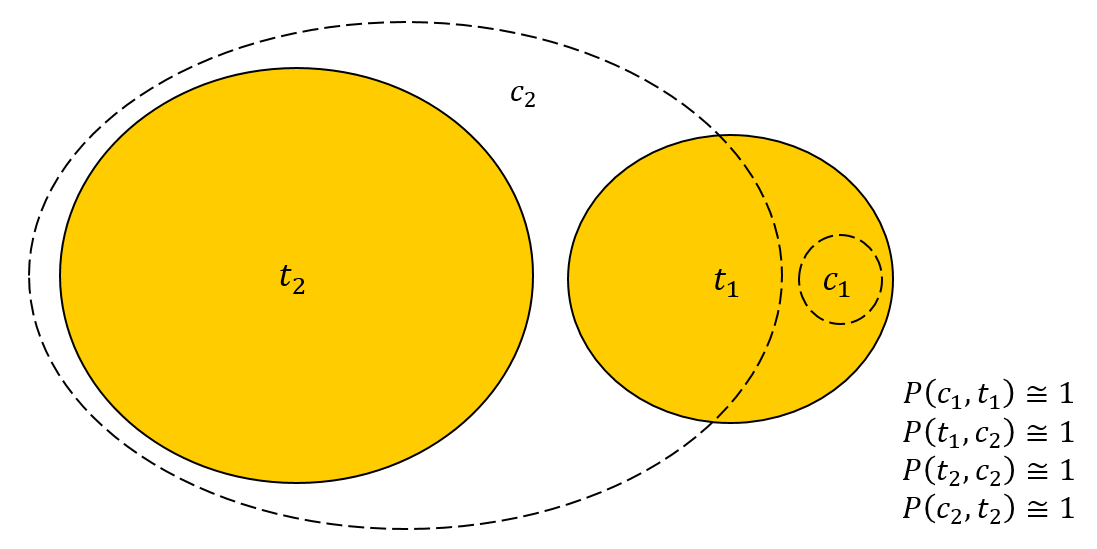
Для примера можно взять ,
,
,
. Кластер
полностью находится внутри
, поэтому:
Отсюда можно вычислить метрики точности для соответствий:
Из этого уже ясно, что показатели Purity и InversePurity высоки для каждого из алгоритмических и эталонных кластеров соответственно. Аккуратное вычисление даёт:
Обе величины близки к единице, хотя для кластера в действительности нет ни одного хорошего представителя из числа алгоритмических кластеров. Метрики не заметили этого, т. к. при подсчёте Purity кластеру
соответствовал кластер
, а при подсчёте InversePurity — кластер
. При вычислении двух различных показателей в качестве оптимальных были выбраны различные соответствия!
Отчасти с этой проблемой помогает справиться F-мера:
Использование такого показателя может быть оправданным в некоторых ситуациях, но стоит иметь в виду, что один и тот же кластер может сопоставиться сразу нескольким эталонам. Кроме того, кластеризация элементов из кластеров, не сопоставленных ни одному из эталонов, не оказывает влияния на значение метрики.
2.3. BCubed-метрики
Этот класс метрик предлагает взглянуть на кластеризацию с точки зрения одного отдельного элемента. Предположим, пользователь изучает конкретный документ внутри новостного сюжета. Какова доля документов этого сюжета, относящихся к той же теме, что и изучаемый документ? А какую долю документы по этой теме в сюжете составляют от числа всех документов по теме?
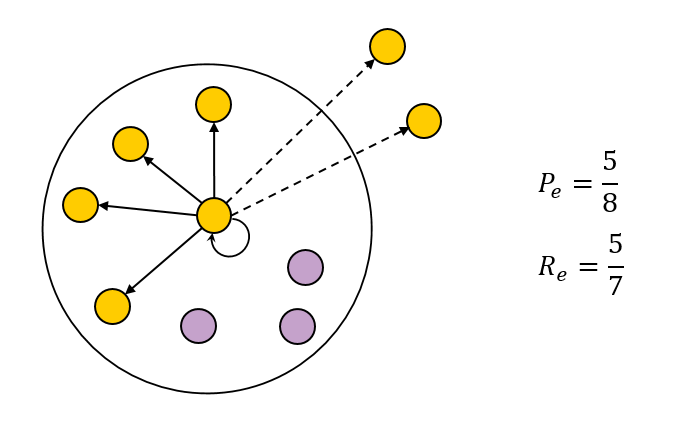
Вполне законные вопросы, и ответ на них приводит к BCubed-метрикам точности и полноты. Они определены для конкретного объекта:
Интегральные показатели определяются усреднением по элементам:
BCubed Precision удовлетворяет свойствам Cluster Homogeneity и Rag Bag, а BCubed Recall — свойствам Cluster Completeness и Size vs Quantity. Сводный показатель — F-мера — удовлетворяет всем четырём свойствам:
3. Метрики эталонных кластеров
В некоторых приложениях полезно оценивать не только интегральные показатели качества, но и качество кластеризации отдельных эталонных кластеров. Поэтому в нашей системе оценки качества все метрики определялись для эталонных кластеров, которые затем агрегировались путём усреднения.
Рассмотрим, как это работает, на следующем примере. Пусть множество объектов состоит из девяти элементов, образующих два эталонных кластера
и
(«зелёный» и «жёлтый» соответственно).
Алгоритмические кластеры не повторяют эталонные в точности: ,
.

3.1. BCubed
Введём BCubed-метрики для отдельных эталонных кластеров:
Для рассмотренного примера получим следующие значения метрики точности кластеризации отдельных элементов:
Отсюда метрики точности эталонных кластеров:
Аналогично для полноты:
Средневзвешенные по всем эталонным кластерам значения BCP и BCR будут такими:
Именно эти характеристики мы и использовали при оценке качества кластеризации.
3.2. Expected Cluster Completeness
Разложение качества кластеризации на характеристики точности и полноты бывает очень полезным для анализа и дальнейшего совершенствования алгоритма. Для принятия решений о том, какой из алгоритмов лучше, требуется, впрочем, выработать один-единственный показатель.
Стандартный способ — F-мера — подходит лишь в ограниченном смысле. Это действительно один показатель, но является ли его значение подходящим для принятия решений? Вовсе не факт.
В конечном счёте требование к алгоритму заключается в том, чтобы каждому эталонному кластеру сопоставить некоторый уникальный алгоритмический кластер, который служил бы для эталона «представителем». Алгоритмический кластер может представлять только один эталонный кластер. При этом из всех сопоставлений важно лишь одно — самое удачное. Такой ход рассуждений является естественным для многих приложений: например, при анализе поисковых запросов судить о содержании кластера проще всего по тексту типичного представителя, то есть единственного запроса.
Сопоставление — функция из множества алгоритмических кластеров в множество эталонных кластеров:
Тогда для конкретного эталона и сопоставления можно вычислить характеристику полноты (cluster completeness):
Среднее значение полноты:
Теперь возникает вопрос — как именно построить сопоставление, то есть функцию . В действительности никакой конкретный алгоритм не будет работать хорошо: незначительные изменения в кластеризации могут существенно повлиять на сопоставление и сильно изменить значение метрики.
Поэтому придётся ввести на множестве всех возможных сопоставлений вероятностную меру и затем вычислить математическое ожидание. Пусть вероятность того, что , равна
Теперь вероятность выбора функции определяется через произведение вероятностей выбора всех её значений:
Теперь можно вычислить ожидаемое покрытие для эталонного кластера:
Интегральный показатель можно определить так:
Либо эквивалентно:
Опишу и другой способ понять эту метрику. Пусть с эталоном пересекаются кластеры
,
, ...,
, пронумерованные в порядке невозрастания размера пересечения:
Кластер выбирается в соответствие эталону
с вероятностью
При этом покрытие будет равно
Поскольку это максимально возможное покрытие, которое может обеспечить один из кластеров, то выбранные для других кластеров сопоставления не играют роли. Так что в этом случае покрытие окажется равным .
Если же для кластера выбрано другое сопоставление, то с вероятностью
эталону
будет сопоставлен кластер
. Тогда покрытие окажется равным
. Это рассуждение можно продолжить, и в конце концов мы получим, что математическое ожидание покрытия равняется
Код для вычисления метрики ECC для конкретного эталонного кластера получается очень простым. Вектор sortedMatchings состоит из всех кластеров, которые пересекаются с эталоном, он отсортирован по неубыванию полноты. Точность и полноту каждого соответствия эталону можно вычислить при помощи методов Precision() и Recall() соответственно. Тогда:
double ExpectedClusterCompleteness(const TMatchings& sortedMatchings) {
double expectedClusterCompleteness = 0.;
double probability = 1.;
for (const TMatching& matching : sortedMatchings) {
expectedClusterCompleteness += matching.Recall() * matching.Precision() * probability;
probability *= 1. - matching.Precision();
}
return expectedClusterCompleteness;
}Интересно, что в этой метрике агрегирующей функцией для точности и полноты в итоге оказалась не -мера, а простое произведение!
Вычислим теперь ECC для эталонных кластеров, с которых начался пункт 3. Максимальное покрытие эталону обеспечивает кластер
, а эталону
—
. Поэтому:
Интегральное значение вычисляется как среднее значение по всем эталонам, поэтому:
4. Реализация
Метрики, описанные в пункте 3, реализованы на C++ и выложены под лицензией MIT на GitHub. Реализация компилируется и запускается как на Linux, так и на Windows.
Программу легко собрать:
git clone https://github.com/yandex/cluster_metrics/ .
cmake .
cmake --build .После этого её можно запустить для того же примера, что разбирался в пункте 3. Расчёты из статьи совпадают с показаниями программы!
./cluster_metrics samples/sample_markup.tsv samples/sample_clusters.tsv
ECC 0.61250 (0.61250)
BCP 0.65125 (0.65125)
BCR 0.65250 (0.65250)
BCF1 0.65187 (0.65187)В скобках указываются значения метрик для «оптимистичного» сценария, когда все неразмеченные элементы в действительности относятся к тем эталонам, с которыми пересекаются содержащие их кластеры. На практике это даже слишком оптимистичная оценка, так как каждый объект может относиться только к одной конкретной теме, но не ко всем сразу. Тем не менее, эта оценка полезна для случаев, когда алгоритм уж очень сильно меняет множество кластеризованных элементов. Если значение метрики существенно меньше оптимистичной оценки — стоит расширить разметку.
5. Как понять, что метрики работают
После того, как метрики придуманы, нужно аккуратно убедиться в том, что они действительно позволяют принимать правильные решения.
Мы построили систему экспертного сравнения алгоритмов кластеризации. Всякий раз, как алгоритм претерпевал существенные изменения, асессоры размечали изменения. Интерфейс, если изображать схематично, выглядел так:

В центре экрана находился эталонный кластер: были перечислены все документы, отнесённые к нему в процессе разметки. С двух сторон от него отображались кластеры, построенные двумя соревнующимися алгоритмами, имеющие непустое пересечение с эталоном. Стороны для алгоритмов выбирались случайным образом, чтобы асессор не знал, с какой стороны находится старый алгоритм, а с какой — новый. Порядок кластеров для каждого алгоритма определялся сортировкой по произведению точности на полноту соответствия — совсем как в метрике ECC!
Зелёным помечались документы, относящиеся к выбранному эталонному кластеру, красным — относящиеся к другому эталонному кластеру. Серым обозначались неразмеченные документы.
Асессор смотрел на этот экран, изучал документы, при необходимости определял правильные эталонные кластеры для неразмеченных документов и в конце концов принимал решение о том, какой из алгоритмов сработал лучше. После разметки нескольких сотен эталонных кластеров можно было получить статистически значимый вывод о превосходстве того или иного алгоритма.
Такую процедуру мы использовали в течение нескольких месяцев, пока не обнаружили, что асессоры всегда выбирают тот алгоритм, для которого выше значение метрики ECC! Если показатели ECC различались хотя бы сколько-то существенно, асессоры всегда выбирали тот же вариант, что и метрика, это происходило буквально в 100% случаев. Поэтому со временем мы отказались от процедуры ручной приёмки и принимали решения просто по метрикам.
Интересно рассказать, что свойства метрик кластеризации из пункта 1 также исследовались на соответствие интуитивным представлениям о качестве кластеризации. В уже цитировавшейся статье описывается следующий эксперимент: для каждого правила формулировался пример — эталонное разбиение некоторого множества объектов и два альтернативных способа кластеризовать эти же объекты.

Пример сравнения двух разбиений на кластеры для свойства Cluster Completeness
Далее сорок асессоров выносили вердикты о том, какой из двух способов лучше, и их ответы сравнивались с вердиктами правил. Оказалось, что с каждым из правил Cluster Homogeneity, Cluster Completeness, Rag Bag не согласился только один из сорока асессоров, а свойству Size vs Quantity не противоречил никто.
Это очень интересное исследование, хотя оно и обладает очевидными недостатками: пример для каждого правила был только один, а восприятие качества кластеризации, очевидно, сильно связано с геометрической интерпретацией.
Уверенности в метриках, описанных в пункте 3, намного больше, так как мы исследовали их на многих сотнях или даже тысячах примеров.
Закончить, однако, хочу предостережением: в каждой новой задаче применимость тех или иных метрик нужно изучать заново. Мне лишь остаётся надеяться, что статья поможет всем, кто будет заниматься этой нелёгкой работой в будущем.

