На данном ресурсе часто говорят о работе со случайными величинами — ну много где они нужны. Иногда случается так, что вам нужно определить зависимость двух случайных величин друг от друга. Тут вы воскликнете — «Пффф, дык мы ж такое в школе проходили — корреляция». Вот тут я хочу вас огорчить — корреляция Пирсона — всего лишь один из множества способов показать зависимость двух случайных величин. К тому же он линейный. То есть, если зависимость между X и Y не линейная, а, допустим, квадратичная, то есть X=Y^2, тогда корреляция Пирсона покажет отсутствие зависимости. Но мы то знаем что это не так. Если вы не задумывались об этом раньше, то сейчас у вас должны появляться идеи — «Как же так?», «А что же делать?», «Аааа, мы все умрем!» Ответы на все эти непростые вопросы я постараюсь дать под катом.
Для начала напомню, что кумулятивные функции распределения могут быть определены на любых множествах значений, но сами имеют значения от 0 до 1. То есть они преобразовывают значения с заданного множества в строго определенный диапазон от 0 до 1. Можно представить, что они «архивируют». Для примера, нормальная функция «архивирует» диапазон от минус бесконечности до плюс бесконечности в этот самый пресловутый (0,1). Логнормальное распределение «архивирует» диапазон только от 0 до бесконечности. И так далее.
А теперь представьте процесс «разархивации». Его проделывают обратные функции распределения. Их так же называют квантильными функциями (quantile function). Суть вы уже поняли — эти функции трансформируют диапазон (0,1) в заданный данной функцией диапазон значений. Все это, естественно, с кучей ограничений, но для «визуального представления», такое сравнение вполне подходит.
Что интересно, если мы возьмем 10^6 случайных величин сгенерированных по одному принципу (например по стандартному нормальному распределению) и еще 10^6 по логнормальному закону распределения:
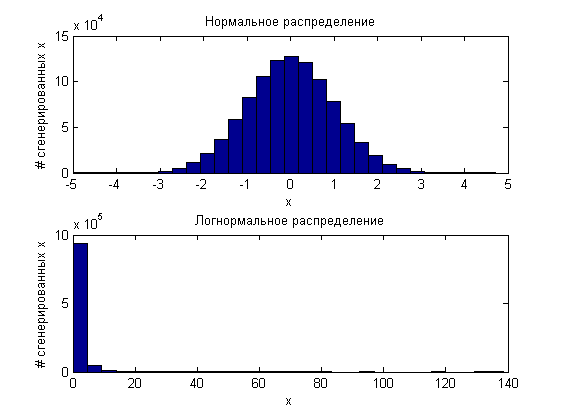
а потом «заархивируем» их, то оба полученных миллиона значений будут равномерно распределены от 0 до 1.
То есть, по сути, любое распределение может быть сгенерировано из равномерно распределённых величин и обратной функции распределения. Была бы такая функция. На этом ликбез закончим.
Теперь представлю вам копулы. Формульное определение звучит так:
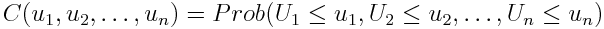
где u — это «архивированное» значение (u = F(x), F — маржинальная функция распределения). Мы так же можем записать, что
То есть это совместная функция распределения нескольких «архивированных» величин. Вы можете сказать — «эээ… мы же только что показали, что „архивированные“ величины одинаково распределены для всех функций распределения». Это верно для отдельных величин, мы же работаем сразу с несколькими. Допустим, у нас есть две величины — одна нормально распределена, другая логнормально. Для начала они будут независимыми друг от друга. Маржинальные (когда мы рассматриваем величины по-отдельности) распределения мы уже показали выше. Теперь я покажу, как выглядит их совместное распределение:
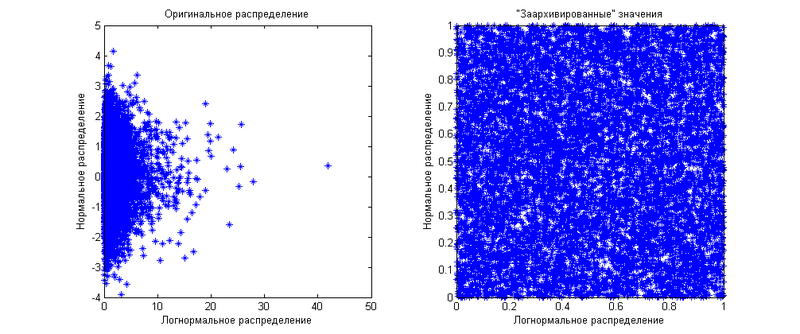
Как видите, «заархивированные» значения равномерно распределены по квадрату 1 на 1. Теперь же мы сгенерируем те же самые величины, но скажем, что между ними есть корреляция равная 0.8. Результат показан на следующем графике
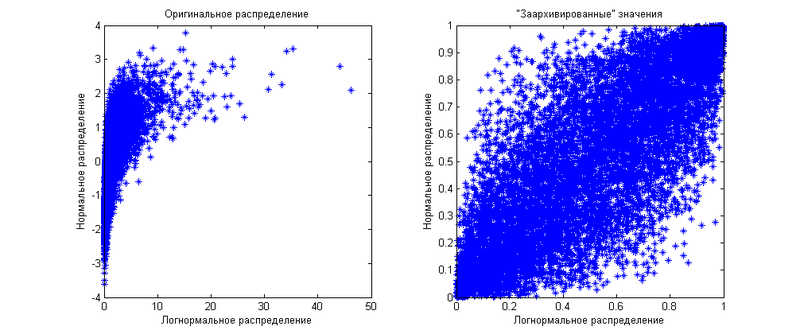
Как видите, теперь распределение «заархивированных» значений неравномерно — оно больше сконцентрировано по диагонали. Тут и проявляется ограниченность использования корреляции, как меры зависимости величин. Оперируя лишь ей, вы сможете распределять «заархивированные» значения только ближе или дальше от диагонали. Диагональ будет либо 45-градусной, если корреляция положительная, либо 135 градусной, если корреляция отрицательная. А что если вы хотите показать другой паттерн зависимости? Вот тут вам и приходят на помощь копулы. Из формульного определения копулы видно, что она показывает функцию распределения на этом квадрате 1 на 1, если величин две. Если же их больше двух, то копула будет показывать распределение в n-мерном кубе 1 на 1 на 1… на 1. Используя различные копулы, вы можете показать любые распределения «заархивированных» величин. Другим немаловажным преимуществом копул является их независимость от маржинальных распределений. То есть вам все равно, какие маржинальные распределения имеют величины — вы работаете непосредственно с зависимостями, выраженными через зависимости «заархивированных» значений.
Так как копула — это все же функция вероятности, а не распределение величин как таковое, графически ее показывают как поверхность, у которой каждая точка равна совместной вероятности двух величин. Иначе говоря — это график плотности совместного распределения. Для наглядности приведу пример нескольких копул:
Для начала покажем саму функцию плотности распределения Гауссовой копулы (gaussian copula) а так же ее графическое отображение:
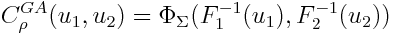
Где
— функция нормального распределения, а 
— обратная функция i-го маржинального распределения, то есть распределения конкретной величины per se.
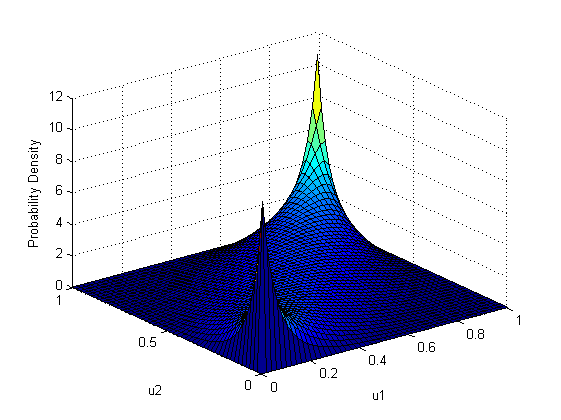
Как видите, она очень напоминает распределение «заархивированных» случайных величин в последнем примере. В этом нет ничего странного, так как в последнем примере использовалась как раз гауссовская копула с тем же параметром корреляции равным 0.8, c нормальной и логнормальной маржинальными функциями распределения.
Дальше хотелось бы показать копулу Стьюдента (Student copula):
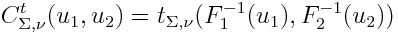
Где t — функция распределения Стьюдента с заданной ковариционной матрицей и заданным количеством степеней свободы
Видно, что в отличие от гауссовой копулы, копула Стьюдента имеет большее значение на крайних значениях (1-1 и 0-0), что означает более толстые хвосты распределения. Еще заметнее высокие значения в углах 0-1 и 1-0, что означает ярко выраженную обратную зависимость на концах диапазонов определений маржинальных функций. Стоит отметить, что данный график строился для положительной корреляции между величинами. В случае нулевой корреляции, в отличие от гауссовой копулы, где в данном случае было бы равномерное распределение по все квадрату, копула Стьюдента имеет одинаковые веса для всех углов. Это означает, что если одна величина принимает «хвостовое» значение, то другая тоже примет «хвостовое» значение, но с одинаковой вероятностью правое или левое. Для удобства прочтения графика плотности копулы можете мысленно делать перпендикулярный одной из осей срез. Полученный график будет графиком плотности вероятности выпадения одной «заархивированной» величины при фиксировании другой.
Еще хотелось бы показать копулу Клейтона (Clayton copula), которая определяет степень связанности двух величин только параметром альфа, который должен быть строго больше 1.
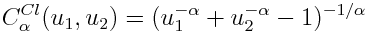
Здесь основной вес лежит на углу 0-0, то есть значения будут скорее принимать значения из левого хвоста маржинальных функций.
В общем, копулы дают возможность показать любую зависимость нескольких величин друг от друга, расширяя диапазон моделирования. Для дальнейшего ознакомления я привожу небольшой список литературы
Копулы в Matlab'е
Understanding relationships using copulas — Edward Frees, Emiliano Valdez
Coping with copulas — Thorsten Schmidt
Для начала напомню, что кумулятивные функции распределения могут быть определены на любых множествах значений, но сами имеют значения от 0 до 1. То есть они преобразовывают значения с заданного множества в строго определенный диапазон от 0 до 1. Можно представить, что они «архивируют». Для примера, нормальная функция «архивирует» диапазон от минус бесконечности до плюс бесконечности в этот самый пресловутый (0,1). Логнормальное распределение «архивирует» диапазон только от 0 до бесконечности. И так далее.
А теперь представьте процесс «разархивации». Его проделывают обратные функции распределения. Их так же называют квантильными функциями (quantile function). Суть вы уже поняли — эти функции трансформируют диапазон (0,1) в заданный данной функцией диапазон значений. Все это, естественно, с кучей ограничений, но для «визуального представления», такое сравнение вполне подходит.
Что интересно, если мы возьмем 10^6 случайных величин сгенерированных по одному принципу (например по стандартному нормальному распределению) и еще 10^6 по логнормальному закону распределения:
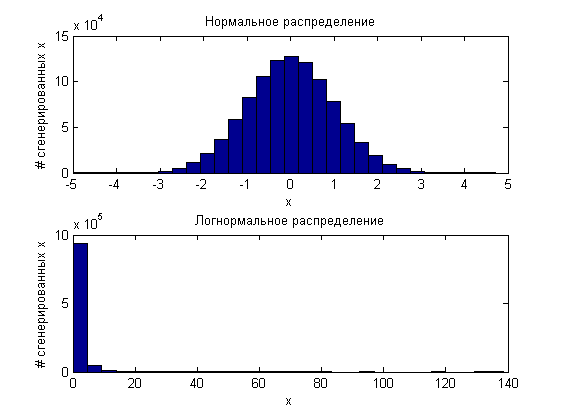
а потом «заархивируем» их, то оба полученных миллиона значений будут равномерно распределены от 0 до 1.
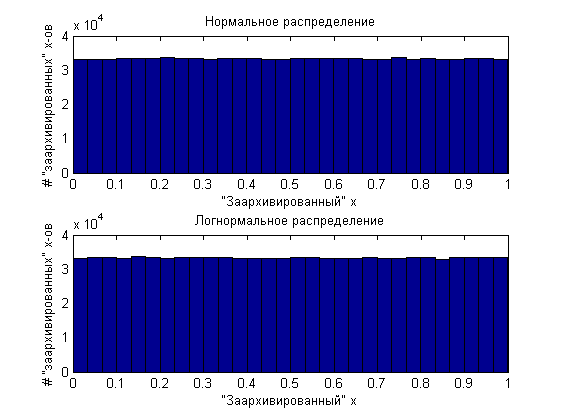
То есть, по сути, любое распределение может быть сгенерировано из равномерно распределённых величин и обратной функции распределения. Была бы такая функция. На этом ликбез закончим.
Теперь представлю вам копулы. Формульное определение звучит так:
где u — это «архивированное» значение (u = F(x), F — маржинальная функция распределения). Мы так же можем записать, что
То есть это совместная функция распределения нескольких «архивированных» величин. Вы можете сказать — «эээ… мы же только что показали, что „архивированные“ величины одинаково распределены для всех функций распределения». Это верно для отдельных величин, мы же работаем сразу с несколькими. Допустим, у нас есть две величины — одна нормально распределена, другая логнормально. Для начала они будут независимыми друг от друга. Маржинальные (когда мы рассматриваем величины по-отдельности) распределения мы уже показали выше. Теперь я покажу, как выглядит их совместное распределение:
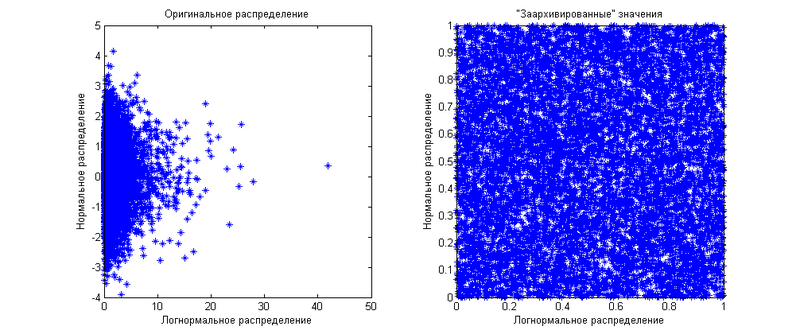
Как видите, «заархивированные» значения равномерно распределены по квадрату 1 на 1. Теперь же мы сгенерируем те же самые величины, но скажем, что между ними есть корреляция равная 0.8. Результат показан на следующем графике
Как видите, теперь распределение «заархивированных» значений неравномерно — оно больше сконцентрировано по диагонали. Тут и проявляется ограниченность использования корреляции, как меры зависимости величин. Оперируя лишь ей, вы сможете распределять «заархивированные» значения только ближе или дальше от диагонали. Диагональ будет либо 45-градусной, если корреляция положительная, либо 135 градусной, если корреляция отрицательная. А что если вы хотите показать другой паттерн зависимости? Вот тут вам и приходят на помощь копулы. Из формульного определения копулы видно, что она показывает функцию распределения на этом квадрате 1 на 1, если величин две. Если же их больше двух, то копула будет показывать распределение в n-мерном кубе 1 на 1 на 1… на 1. Используя различные копулы, вы можете показать любые распределения «заархивированных» величин. Другим немаловажным преимуществом копул является их независимость от маржинальных распределений. То есть вам все равно, какие маржинальные распределения имеют величины — вы работаете непосредственно с зависимостями, выраженными через зависимости «заархивированных» значений.
Так как копула — это все же функция вероятности, а не распределение величин как таковое, графически ее показывают как поверхность, у которой каждая точка равна совместной вероятности двух величин. Иначе говоря — это график плотности совместного распределения. Для наглядности приведу пример нескольких копул:
Для начала покажем саму функцию плотности распределения Гауссовой копулы (gaussian copula) а так же ее графическое отображение:
Где
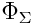— функция нормального распределения, а 
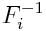— обратная функция i-го маржинального распределения, то есть распределения конкретной величины per se.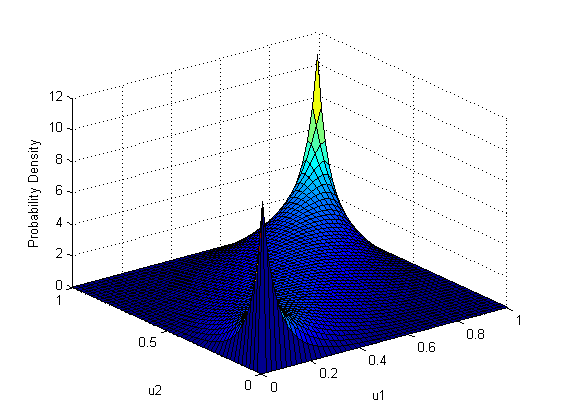 
Как видите, она очень напоминает распределение «заархивированных» случайных величин в последнем примере. В этом нет ничего странного, так как в последнем примере использовалась как раз гауссовская копула с тем же параметром корреляции равным 0.8, c нормальной и логнормальной маржинальными функциями распределения.
Дальше хотелось бы показать копулу Стьюдента (Student copula):
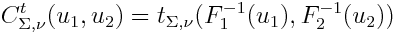
Где t — функция распределения Стьюдента с заданной ковариционной матрицей и заданным количеством степеней свободы
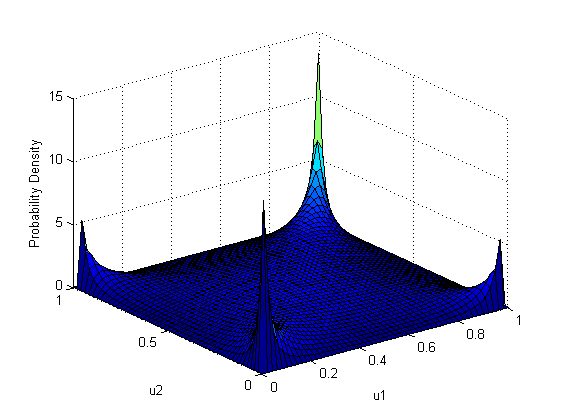
Видно, что в отличие от гауссовой копулы, копула Стьюдента имеет большее значение на крайних значениях (1-1 и 0-0), что означает более толстые хвосты распределения. Еще заметнее высокие значения в углах 0-1 и 1-0, что означает ярко выраженную обратную зависимость на концах диапазонов определений маржинальных функций. Стоит отметить, что данный график строился для положительной корреляции между величинами. В случае нулевой корреляции, в отличие от гауссовой копулы, где в данном случае было бы равномерное распределение по все квадрату, копула Стьюдента имеет одинаковые веса для всех углов. Это означает, что если одна величина принимает «хвостовое» значение, то другая тоже примет «хвостовое» значение, но с одинаковой вероятностью правое или левое. Для удобства прочтения графика плотности копулы можете мысленно делать перпендикулярный одной из осей срез. Полученный график будет графиком плотности вероятности выпадения одной «заархивированной» величины при фиксировании другой.
Еще хотелось бы показать копулу Клейтона (Clayton copula), которая определяет степень связанности двух величин только параметром альфа, который должен быть строго больше 1.
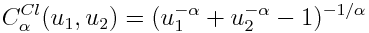
Здесь основной вес лежит на углу 0-0, то есть значения будут скорее принимать значения из левого хвоста маржинальных функций.
В общем, копулы дают возможность показать любую зависимость нескольких величин друг от друга, расширяя диапазон моделирования. Для дальнейшего ознакомления я привожу небольшой список литературы
Копулы в Matlab'е
Understanding relationships using copulas — Edward Frees, Emiliano Valdez
Coping with copulas — Thorsten Schmidt
