Comments 149
Красиво!)
+1
А в первой задаче «нижняя» окружность разве не будет эллипсом?
+1
Нет. Мы изначально взяли конус, где нижняя хрень — окружность.
+7
Фикс:
Хрень = основание
Хрень = основание
+19
Понял, то есть конус не прямой. Тогда такой вопрос, если прямой конус резать не параллельно основанию (не перпендикулярно оси вращения), то получится эллипс. А для не прямого, возможно если резать не параллельно основанию тоже выйдет эллипс? Не должны ли нижняя и верхняя окружность лежать в параллельных плоскостях? (не настаиваю, пытаюсь для себя разобраться)
+2
Для непрямого конуса, почти всегда выйдет эллипс, но есть две замечательные плоскости, которые высекает именно окружность. Одна плоскость, параллельна основанию, а вторая — нет.
0
Все равно не понимаю почему центры не совпадают.
+1
Я только что понял, что я рисунок немного неправдоподобно нарисовал. Эта секущая плоскость должна быть чуть наклоннее.
А вообще, то что центры не совпадают можно доказать прямыми выкладками.
А вообще, то что центры не совпадают можно доказать прямыми выкладками.
0
Отрезки от вершины к середине окружности — это медианы треугольников, которые получаются, если конус разрезать вертикальной плоскостью. Медианы из одинаковых углов не обязаны совпадать, это только биссектрисы делают.
Интереснее послушать доказательство существования двух непараллельных плоскостей, которые могут вырезать круг из такого конуса.
Интереснее послушать доказательство существования двух непараллельных плоскостей, которые могут вырезать круг из такого конуса.
+2
то что они не обязаны — никак не доказывает что они не могут.
мой вгляд (уже на более 10 лет далекий от стереометрии или как это называется). возьмем центр окружности (верхней, не паралельной), и проведем через эту точку плоскость паралельную основанию, может я чего-то и забыл, но она тоже будет кругом.
Вот тут я возможно ошибась, но центр этого нового круга будет в той же точке, через которую мы провели секущую плоскость. Т.е. они совпадут.
Центр новой окружности — будет совпадать по проекции с центром нижней, а центр второй — там же.
мой вгляд (уже на более 10 лет далекий от стереометрии или как это называется). возьмем центр окружности (верхней, не паралельной), и проведем через эту точку плоскость паралельную основанию, может я чего-то и забыл, но она тоже будет кругом.
Вот тут я возможно ошибась, но центр этого нового круга будет в той же точке, через которую мы провели секущую плоскость. Т.е. они совпадут.
Центр новой окружности — будет совпадать по проекции с центром нижней, а центр второй — там же.
0
то что они не обязаны — никак не доказывает что они не могут
Доказывается легко — возьмем угол и два отрезка с концами на сторонах угла, не параллельные друг другу такие, что их середины и вершина угла лежат на одний прямой. Проведем отрезок, параллельный одному из них, через конец другого — медиана, очевидно, будет и его медианой тоже. Тогда у нас получится треугольник из двух отрезков и куска стороны угла, причем медиана угла делит две стороны пополам. Но тогда она должна быть паралллельной третьей стороне. Противоречие.
0
Можно наверное отрезать параллельно нижней, а потом повернуть вокруг оси вращения. Но придется вращать на 180 градусов, так как сечение в перпендикулярное оси — эллипс, у нужно чтобы границы совпали после вращения. То есть вроде как вторая плоскость рассекает под тем же углом к оси, только как зеркальное отражение.
+1
А можете привести ссылку (книга, веб — не важно) подтверждающее это утверждение? Ну или доказательство.
+1
Я тоже обыскался.
+1
Возьмём эллиптический конус
z^2=a^2*x^2+y^2, где a>1.
Пересечем его плоскостью, заданной параметрически:
x=b*u, y=v, z=1+c*u,
где b^2=2/(1+a^2), c^2=(a^2-1)/(a^2+1).
Поскольку b^2+c^2=1, система координат (u,v) на этой плоскости декартова (направляющие векторы (b,0,c) и (0,1,0) равны и перпендикулярны). Подставив x,y,z в уравнение конуса, получим:
0=a^2*b^2*u^2+v^2-1-2*c*u-c^2*u^2=v^2+u^2*(2*a^2-(a^2-1))/(a^2+1)-2*c*u-1=v^2+(u-c)^2-(1+c^2)
Это уравнение окружности радиусом sqrt(1+c^2).
Если мы возьмём b>0, c>0, то получим одно сечение, а если b>0, c<0 — то другое. В обох случаях сечение будет окружностью. Плоскости, очевидно, непараллельны.
z^2=a^2*x^2+y^2, где a>1.
Пересечем его плоскостью, заданной параметрически:
x=b*u, y=v, z=1+c*u,
где b^2=2/(1+a^2), c^2=(a^2-1)/(a^2+1).
Поскольку b^2+c^2=1, система координат (u,v) на этой плоскости декартова (направляющие векторы (b,0,c) и (0,1,0) равны и перпендикулярны). Подставив x,y,z в уравнение конуса, получим:
0=a^2*b^2*u^2+v^2-1-2*c*u-c^2*u^2=v^2+u^2*(2*a^2-(a^2-1))/(a^2+1)-2*c*u-1=v^2+(u-c)^2-(1+c^2)
Это уравнение окружности радиусом sqrt(1+c^2).
Если мы возьмём b>0, c>0, то получим одно сечение, а если b>0, c<0 — то другое. В обох случаях сечение будет окружностью. Плоскости, очевидно, непараллельны.
+3
Более того, если интеграл от синуса по какому-то любому отрезку равен нулю, то смело можно считать, что длина этого отрезка кратна числу 2пи.
А как же, например [-0.0001, 0.0001]? Интеграл 0 за счет нечетности sin, а кратности 2пи нет. Дырка в доказательстве?
+4
Вы абсолютно правы. Я написал бред.
На самом деле надо было так написать:
берем ставим начало координат в нижнем левом углу стены. Интеграл распадется на произведение двух интегралов. Один из интегралов равен нулю и есть интеграл от нуля до чего-то. И теперь из этого следует, что «чего-то» — целое.
Спасибо.
Сейчас поправлю.
На самом деле надо было так написать:
берем ставим начало координат в нижнем левом углу стены. Интеграл распадется на произведение двух интегралов. Один из интегралов равен нулю и есть интеграл от нуля до чего-то. И теперь из этого следует, что «чего-то» — целое.
Спасибо.
Сейчас поправлю.
0
По первой задаче такой вопрос — известно, что есть по меньшей мере одна точка (цент окружности конуса), которая при таком переносе с плоскости на плоскость не переходит сама в себя, грубо говоря. Видимо, нужно доказать, что такое не случится ни с какой точкой из тех, которые мы будем использовать в построении. То есть не факт, что проекция с одной плоскости на другую реально отобразит наш алгоритм, по-моему.
0
Дело в том, что все точки, которые мы используем в алгоритме получены как точки пересечения. А эти точки пересечения точно переходят друг в друга.
Еще раз:
Считайте, что алгоритм — это прога на компьютере. Что может делать эта прога:
1) В рандомном месте рисовать прямые. Притом конечный результат алгоритма не должен, очевидно, зависеть от рандомности.
2) Соединять какие-то определенные точки (получившиеся от пересечений).
Больше ничего прога не умеет делать. Раз от рандомности ничего не должно зависеть, то можно предположить, что если прога нарисовала на верхней плоскости какую-то рандомную прямую, то пусть на нижней плоскости эта же прога нарисует ее тень. Ну а при соединении определенных точек (получившихся от пересечений) прямыми, очевидно на нижней плоскости получится тень верхней.
Еще раз:
Считайте, что алгоритм — это прога на компьютере. Что может делать эта прога:
1) В рандомном месте рисовать прямые. Притом конечный результат алгоритма не должен, очевидно, зависеть от рандомности.
2) Соединять какие-то определенные точки (получившиеся от пересечений).
Больше ничего прога не умеет делать. Раз от рандомности ничего не должно зависеть, то можно предположить, что если прога нарисовала на верхней плоскости какую-то рандомную прямую, то пусть на нижней плоскости эта же прога нарисует ее тень. Ну а при соединении определенных точек (получившихся от пересечений) прямыми, очевидно на нижней плоскости получится тень верхней.
0
Притом конечный результат алгоритма не должен, очевидно, зависеть от рандомности
А эти точки пересечения точно переходят друг в друга.
Да, понял. Действительно, если речь идет строго только о точках, прямых и пересечениях, то можно говорить о полном соответствии алгоритма. Спасибо!
+1
Если мы можем строить «тени» от существующих прямых, то мы легко можем найти центр окружности.
0
UFO just landed and posted this here
В этом комментарии описывается, как бороться с нарушением порядка при проективном преобразовании.
0
>>Аналогию, наверное, можно провести, например, с этой оптической иллюзией:
>>Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.
При всём уважении, тут 3 шестиугольника и 3 четырёхугольника. От силы — 6 плоскостей в пространстве, но никак не кубы в той или иной форме.
>>Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.
При всём уважении, тут 3 шестиугольника и 3 четырёхугольника. От силы — 6 плоскостей в пространстве, но никак не кубы в той или иной форме.
+1
>>Тут видишь то большой куб с выпиленным куском, то маленький кубик, стоящий в углу.
Увидел ещё один вариант, там два кубика странно расположенных по отношению друг к другу.
Увидел ещё один вариант, там два кубика странно расположенных по отношению друг к другу.
+4
Я его называю кристалл соли с дефектом :) А вообще очень немногие почему-то могут это представить, даже если прямо говоришь представить два параллелепипеда
0
Увидел его когда усердно пытался разглядеть отпиленный угол.
Отпиленный угол разглядел в последнюю очередь :)
Отпиленный угол разглядел в последнюю очередь :)
+1
Я тоже с трудом смог представить «кристалл соли», как Вы его назвали.
А представить сложно вот почему: на оригинальном изображении в изометрии каждая пара параллельных плоскостей подкрашена отдельным цветом — читай воображаемый источник света одинаково подсвечивает параллельные поверхности. Поэтому, не напрягаясь, мозг распознает то большой куб с маленьким выпиленным, то маленький куб в углу. На это и рассчитана светотень.
Я поменял местами эти же цвета, и представить «кристалл соли с дефектом» стало значительно проще (по крайней мере мне):

А представить сложно вот почему: на оригинальном изображении в изометрии каждая пара параллельных плоскостей подкрашена отдельным цветом — читай воображаемый источник света одинаково подсвечивает параллельные поверхности. Поэтому, не напрягаясь, мозг распознает то большой куб с маленьким выпиленным, то маленький куб в углу. На это и рассчитана светотень.
Я поменял местами эти же цвета, и представить «кристалл соли с дефектом» стало значительно проще (по крайней мере мне):

+1
А вы попробуйте увидеть выемку странной формы :) У меня пока не получилось.
+1
Я вижу маленький параллелепипед, стоящий в углу, потому что свет обычно падает сверху.
0
Странное доказательство 1й задачи.
Для доказательства выдвинули смелую теорию, что тень центра не попадает в центр и на основе этого доказываем, что задача решается.
Тогда надо и понятие «тень» вводить более формально и доказывать, что центры не совпадут.
Это как доказывать что параллельные прямые не пересекаются.
Пусть прямые мы строим как окружности. Тогда при достаточном удалении друг от друга любые две прямые не пересекаются. А значит и 2 параллельные прямые не будут пересекаться.
Для доказательства выдвинули смелую теорию, что тень центра не попадает в центр и на основе этого доказываем, что задача решается.
Тогда надо и понятие «тень» вводить более формально и доказывать, что центры не совпадут.
Это как доказывать что параллельные прямые не пересекаются.
Пусть прямые мы строим как окружности. Тогда при достаточном удалении друг от друга любые две прямые не пересекаются. А значит и 2 параллельные прямые не будут пересекаться.
+4
UFO just landed and posted this here
параллельны, то коэффициент использования площади досок не увеличится, но может уменьшится, если появятся пересечения
Докажите.
0
UFO just landed and posted this here
а докажите, что у идеального расположения досок этот ваш определенный «коэффициент покрытия» будет максимальными среди всех возможных.
0
Еще вам нужно доказать, что чем больше коэффициент, тем лучше покрытие, то есть тем меньше сумма ширин досок.
0
Например, две положенные крест на крест доски возле края окружности могут покрыть большую площадь, чем лёжа рядом.
А вот площадь на такой полусфере покроют меньшую.
Собственно, площадь на полусфере и есть мерило коэффициента, который вы упомянули.
А вот площадь на такой полусфере покроют меньшую.
Собственно, площадь на полусфере и есть мерило коэффициента, который вы упомянули.
+2
>>Например, две положенные крест на крест доски возле края окружности могут покрыть большую площадь, чем лёжа рядом.
Это как, простите? А, паралельные доски кладём у края, одна из скрещивающихся будет проходить через центр? Смешно.
Надо танцевать от площади. Есть участок, который надо покрыть. То, что покрывающие его доски крест-на-крест будут иметь ширину большую чем паралельные доказывать надо?..
Это как, простите? А, паралельные доски кладём у края, одна из скрещивающихся будет проходить через центр? Смешно.
Надо танцевать от площади. Есть участок, который надо покрыть. То, что покрывающие его доски крест-на-крест будут иметь ширину большую чем паралельные доказывать надо?..
0
Если этот участок уже имеет форму креста (например, обычный крестик, составленный из 5 квадратов), то доски, лежащие крест-накрест, будут иметь меньшую ширину. В реальности такого участка не встретится, но может остаться несколько незакрытых областей в разных местах колодца, и их тоже иногда выгоднее будет покрывать перекрещивающимися досками.
+1
0
Рассуждение к первой задаче не является доказательством. Сечения не параллельные основанию конуса являются не являются окружностями (эллипс, парабола, гипербола, ничего, но не окружность)
0
Да, не все сечения являются окружностями. Но мы проводим именно то сечение, которое высекает окружность. Это всегда возможно.
0
Процитирую:
а) — секущая плоскость пересекает все образующие конуса в точках одной его полости; линия пересечения — замкнутая овальная кривая — эллипс, в частности, когда плоскость перпендикулярна оси конуса, — окружность;
-1
И как вы этим опровергли то, что я сказал комментарием выше? (Наш конус не прямой, а в вашей цитате предполагается, что прямой)
0
А это неважно. При построении одной линейкой нам абсолютно плевать, окружность перед нами или эллипс. Построение линейкой использует только проективные свойства плоскости.
0
Это очень важно так как у эллипса нет центра.
+2
Да, но само по себе это не гарантирует, что у эллипса должен получиться именно центр. Другое дело, что поскольку алгоритма построения не существует, мы можем делать из его существования какие угодно выводы.
0
Мне очень нравится теорема, только она не из геометрии.
Для любого алгоритма сжатия без потерь существует текст произвольной длины n, такой что этот алгоритм не сможет сжать этот текст.
А доказательство очень простое, и, имхо, красивое.
Для любого алгоритма сжатия без потерь существует текст произвольной длины n, такой что этот алгоритм не сможет сжать этот текст.
А доказательство очень простое, и, имхо, красивое.
+1
Решения первой задачи рассчитано на людей, не знающих высшую математику. Проблема в том, что для понимания его корректности желательно знать высшую математику =)
+1
Высшая математика тут ни при чём. Начертательная геометрия обычно не выходит в дисциплины «вышки».
+1
С каких пор начерталка занимается доказательствами?
0
А с каких пор аналитическая геометрия, единственная включаемая в дисциплины «вышки», занимается построениями с линейкой?
+2
Во-первых, здесь используется проективная геометрия. Во-вторых, я не вижу причин, почему ей нельзя заниматься построениями с линейкой.
+1
Возможно, потому, что понятие алгоритма, или произвольных цепочек построений (пусть даже определяемых через отношения принадлежности), входит не в геометрию, а в математическую логику. Теоремы геометрии обычно содержат конечное множество объектов (или бесконечное, но хорошо проиндексированное). В сущности, тут надо доказать, что g(F(X))=F(g(X)), где g — проекция, F — формула, описывающая построение, а X — выбранные произвольные точки (на окружности и не только) для всех наборов точек и всех формул… Это уже трудно назвать элементарной математикой.
0
Товарищ Sirion как раз утверждает, что это из высшей математики. И после упоминания проективной геометрии, я вынужден признать, что он прав, эта задача скорее относится к высшей математике, чем не относится к ней. Т.к. проективная геометрия может использовать методы «аналгема».
+1
А разве понятие алгоритма входит не в теорию алгоритмов? Впрочем, неважно. По сути да, такое доказательство не будет производиться средствами исключительно проективки. Но проективка будет в нём существенно использоваться. С другой стороны, начерталка — дисциплина сугубо прикладная. Я не вижу, как она может хотя бы использоваться в доказательстве.
0
Кстати, отпишитесь те, кто не гей пытался сам решать задачи перед тем, как смотреть решения. Как у вас успехи? Я пока решил первые две. Вторую, кстати, существенно проще и нагляднее, чем у автора.
+2
Первую я и так знал. Вторую, вроде бы, решил — через сумму проекций сторон. Пока ошибок не вижу, но записать ещё не пытался. Третью решил с ошибкой, сейчас думаю, как исправить. С четвёртой пока глухо.
0
Третью пытались решать по индукции?
+1
Авторское решение третьей задачи шикарно. Я решил её тупо в лоб.
+1
В четвёртой нужную функцию нашёл подбором. Со сферой и тенями, конечно, красивше.
+1
Про кирпичную стену: если у прямоугольника есть одна целая сторона, то у него должна быть и вторая.
+6
>Окружность и линейка
>тень найденного центра «верхней» окружности не попадает в центр «нижней».
Да ну? Проведём плоскость перпендикулярно окружностям через их центры.
Получим: угол (образующие конуса), и 2 параллельных отрезка(диаметры окружностей). В серединах этих параллельных отрезков будут точки — центры окружностей (X и X').
habrastorage.org/storage2/22b/49d/c69/22b49dc6935bc34f7b698a994bdbbcf1.png
Треугольники ACX и A'CX' подобны (по 3м углам), следовательно центры лежат на одной прямой.
На самом деле невозможность связана с тем, что линейка эквивалентна простым арифметическим действиям, а чтобы найти центр окружности нужно проинтегрировать радиус-вектор от -pi до pi и разделить полученное на 2pi — это и будет радиус-вектор центра. Но линейка не умеет интегрировать, а тем более — делить на пи, так как пи — число трансцендентное (почитайте о квадратуре круга).
С остальными задачами на первый взгляд всё хорошо (второго не было).
>тень найденного центра «верхней» окружности не попадает в центр «нижней».
Да ну? Проведём плоскость перпендикулярно окружностям через их центры.
Получим: угол (образующие конуса), и 2 параллельных отрезка(диаметры окружностей). В серединах этих параллельных отрезков будут точки — центры окружностей (X и X').
habrastorage.org/storage2/22b/49d/c69/22b49dc6935bc34f7b698a994bdbbcf1.png
Треугольники ACX и A'CX' подобны (по 3м углам), следовательно центры лежат на одной прямой.
На самом деле невозможность связана с тем, что линейка эквивалентна простым арифметическим действиям, а чтобы найти центр окружности нужно проинтегрировать радиус-вектор от -pi до pi и разделить полученное на 2pi — это и будет радиус-вектор центра. Но линейка не умеет интегрировать, а тем более — делить на пи, так как пи — число трансцендентное (почитайте о квадратуре круга).
С остальными задачами на первый взгляд всё хорошо (второго не было).
-2
Отрезки, которые диаметры окружностей, будут непараллельны. На вашем чертеже AB следовало бы нарисовать почти вертикально. Треугольники ABC и B'A'C будут подобны (именно в таком порядке — с переставленными B' и A'), а точки С, X и X' окажутся не на одной прямой — лучи CX и CX' будут симметричны относительно биссектрисы угла.
+2
КМК, если использовать линейку как отвес, то можно:
1. Расположить лист для рисования окружности ниже линейки и перпендикулярно ей (отвесу), поставить точку (она и будет центром будущей окружности).
2. Чуть поднимем лист (или опустим линейку), теперь нам придется линейку наклонить относительно перпендикуляра к листу/плоскости.
3. Делаем линейкой круговое движение и рисуем ею (линейкой) окружность, с центром там, где мы его отметили в п.1…
Так, конечно, нарушается условие
1. Расположить лист для рисования окружности ниже линейки и перпендикулярно ей (отвесу), поставить точку (она и будет центром будущей окружности).
2. Чуть поднимем лист (или опустим линейку), теперь нам придется линейку наклонить относительно перпендикуляра к листу/плоскости.
3. Делаем линейкой круговое движение и рисуем ею (линейкой) окружность, с центром там, где мы его отметили в п.1…
Так, конечно, нарушается условие
ею можно соединять любые заданные точки на плоскости, все остальное, кажется, соответствует условию задачи?
0
В оптической иллюзии про куб, кстати, есть еще один вариант. Маленький параллелпипед торчит из большого под тупым углом к нему, если опустить привязки цветов к граням, нормали которых, направлены в одну сторону.
+2
Куда вы придете если будете все время идти (а по морю плыть) на северо-восток?
0
Никуда — по пути голова закружится
+1
Через бесконечное число оборотов — на северный полюс. А к чему это?
0
На Северный полюс наверное. Что-то вроде нулевого меридиана (может криво сформулировано, не помню уже географии), дальше будет не север и не восток =)
-1
Про кирпичи.
Представим нашу доску в виде ориентированного графа. Вершины графа — отрезки, являющиеся объединением вертикальных сторон кирпичей, рёбра — сами кирпичи. Каждая вершина и каждое ребро снабжены числом («ключом»). Для вершины это x-координата, для ребра — высота кирпича. «Старт» — вершина, соответствующая левой стороне доски, «Финиш» — правая сторона.
Из условия задачи следуют два условия на граф:
1) сумма ключей рёбер, входящих в какую-нибудь вершину (кроме старта и финиша) равна сумме ключей рёбер, выходящих из неё;
2) каждое ребро либо снабжено целым ключом, либо соединяет две вершины, разность ключей которых целая.
Допустим, что в графе есть хотя бы одно ребро AB, ключ которого не является целым. Тогда оно соединяет вершины, разность ключей которых целая. Если мы стянем это ребро (удалим его вместе с вершиной B, а рёбра, которые шли в вершину B или из неё, переключим на вершину A), то условия 1 и 2 не нарушатся. То, что при стягивании могут появиться рёбра, идущие из финиша, нас не пугает — ацикличности графа мы не требовали.
Продолжаем этот процесс, пока возможно. В конце есть два варианта.
— либо нам удалось стянуть ребро, соединяющее старт и финиш. Это означает, что разность ключей старта и финиша была целым числом, т.е. доска имела целую ширину.
— либо остались только рёбра с целыми ключами. Значит, сумма ключей рёбер, выходящих из старта (минус сумма ключей рёбер, входящих в старт) является целым числом, а она равна высоте доски.
Что и требовалось доказать. И никаких интегралов.
Представим нашу доску в виде ориентированного графа. Вершины графа — отрезки, являющиеся объединением вертикальных сторон кирпичей, рёбра — сами кирпичи. Каждая вершина и каждое ребро снабжены числом («ключом»). Для вершины это x-координата, для ребра — высота кирпича. «Старт» — вершина, соответствующая левой стороне доски, «Финиш» — правая сторона.
Из условия задачи следуют два условия на граф:
1) сумма ключей рёбер, входящих в какую-нибудь вершину (кроме старта и финиша) равна сумме ключей рёбер, выходящих из неё;
2) каждое ребро либо снабжено целым ключом, либо соединяет две вершины, разность ключей которых целая.
Допустим, что в графе есть хотя бы одно ребро AB, ключ которого не является целым. Тогда оно соединяет вершины, разность ключей которых целая. Если мы стянем это ребро (удалим его вместе с вершиной B, а рёбра, которые шли в вершину B или из неё, переключим на вершину A), то условия 1 и 2 не нарушатся. То, что при стягивании могут появиться рёбра, идущие из финиша, нас не пугает — ацикличности графа мы не требовали.
Продолжаем этот процесс, пока возможно. В конце есть два варианта.
— либо нам удалось стянуть ребро, соединяющее старт и финиш. Это означает, что разность ключей старта и финиша была целым числом, т.е. доска имела целую ширину.
— либо остались только рёбра с целыми ключами. Значит, сумма ключей рёбер, выходящих из старта (минус сумма ключей рёбер, входящих в старт) является целым числом, а она равна высоте доски.
Что и требовалось доказать. И никаких интегралов.
0
Раз пошла такая пьянка, вот моё решение второй задачи. Пусть рёбра внешнего ящика равны a, b, c, а внутреннего — x, y, z.
Самый длинный отрезок, который можно запихнуть в ящик, равен диагонали этого ящика. Значит, диагональ внутреннего ящика не больше диагонали внешнего. Отсюда следует, что а2+ b2+ c2 >= x2 + y2 + z2.
Далее, несложно показать, что поверхность внутреннего ящика не больше поверхности внешнего. Для этого выделим на поверхности внешнего ящика шесть участков, которые, будучи ортогонально спроектированы на соответствующие грани внутреннего ящика, покроют их. Следовательно, 2ab + 2bc + 2ac >= 2xy + 2yz + 2zx.
Просуммируем. а2+ b2+ c2 + 2ab + 2bc + 2ac >= x2 + y2 + z2 + 2xy + 2yz + 2zx.
(a + b + c)2 >= (x + y + z)2
a + b + c >= x + y + z, что и требовалось доказать.
Самый длинный отрезок, который можно запихнуть в ящик, равен диагонали этого ящика. Значит, диагональ внутреннего ящика не больше диагонали внешнего. Отсюда следует, что а2+ b2+ c2 >= x2 + y2 + z2.
Далее, несложно показать, что поверхность внутреннего ящика не больше поверхности внешнего. Для этого выделим на поверхности внешнего ящика шесть участков, которые, будучи ортогонально спроектированы на соответствующие грани внутреннего ящика, покроют их. Следовательно, 2ab + 2bc + 2ac >= 2xy + 2yz + 2zx.
Просуммируем. а2+ b2+ c2 + 2ab + 2bc + 2ac >= x2 + y2 + z2 + 2xy + 2yz + 2zx.
(a + b + c)2 >= (x + y + z)2
a + b + c >= x + y + z, что и требовалось доказать.
+2
Нетрудно показать, что сумма длин проекций любого отрезка на три перпендикулярных прямых не меньше длины этого отрезка.
С другой стороны, длина проекции ящика на прямую равна 1/4 суммы длин проекций его рёбер (это легко проверить).
Значит, сумма длин проекций ящика на три перпендикулярных прямых равна 1/4 суммы длин проекций его рёбер на эти прямые, т.е. не меньше суммы длин рёбер ящика, что, в свою очередь, равно сумме измерений ящика.
Доказано.
С другой стороны, длина проекции ящика на прямую равна 1/4 суммы длин проекций его рёбер (это легко проверить).
Значит, сумма длин проекций ящика на три перпендикулярных прямых равна 1/4 суммы длин проекций его рёбер на эти прямые, т.е. не меньше суммы длин рёбер ящика, что, в свою очередь, равно сумме измерений ящика.
Доказано.
0
Вторая половина пишется в три строчки: либо есть путь из старта в финиш (в неориентированном графе), идущий только по рёбрам с нецелыми ключами — тогда разность ключей старта и финиша целая, либо можно выделить множество вершин S, содержащее старт, но не содержащее финиша, для которого все идущие в S или из S рёбра имеют целые ключи — тогда поток из старта в финиш целый.
0
Решение задачи поиска центра окружности.
Провожу любую прямую, пересекающую окружность. Выбираю точку внутри окружности, но не на этой прямой. Далее, провожу через эту точку случайные прямые до тех пор, пока не окажется, что построенная прямая не пересекает первую нарисованную прямую (это может занять бесконечное время, но у нас в запасе универсум). Потом так же строю вторую пару параллельных прямых, пересекающих первую пару. А имея две пары параллельных прямых, найти центр окружности — дело техники.
Провожу любую прямую, пересекающую окружность. Выбираю точку внутри окружности, но не на этой прямой. Далее, провожу через эту точку случайные прямые до тех пор, пока не окажется, что построенная прямая не пересекает первую нарисованную прямую (это может занять бесконечное время, но у нас в запасе универсум). Потом так же строю вторую пару параллельных прямых, пересекающих первую пару. А имея две пары параллельных прямых, найти центр окружности — дело техники.
+1
Далее, провожу через эту точку случайные прямые до тех пор, пока не окажется, что построенная прямая не пересекает первую нарисованную прямую (это может занять бесконечное время, но у нас в запасе универсум).Не работает. Мощность множества прямых, проведённых через точку — континуум, мощность множества попыток алгоритма — счётное. Вероятность проведения параллельной прямой за бесконечное число попыток равна нулю.
+1
Mrrl Подсказал как можно найти центр окружности в первой задаче.
1. Строим бесконечную прямую касательную к окружности в плоскости окружности.
2. С противоположной стороны окружности строим еще одну касательную параллельную первой прямой, т.к. линейка и прямые бесконечны, то мы можем построить такую прямую.
3. Соединяем точки касания отрезком. Это диаметр окружности.
4. Аналогичным образом строим другие две бесконечных касательных к окружности не совпадающие с первыми касательными.
5. Соединяем две новые точки касания между собой. Это еще один диаметр окружности отличный от найденного в п.3.
6. Точка пересечения двух диаметров будет центром окружности.
1. Строим бесконечную прямую касательную к окружности в плоскости окружности.
2. С противоположной стороны окружности строим еще одну касательную параллельную первой прямой, т.к. линейка и прямые бесконечны, то мы можем построить такую прямую.
3. Соединяем точки касания отрезком. Это диаметр окружности.
4. Аналогичным образом строим другие две бесконечных касательных к окружности не совпадающие с первыми касательными.
5. Соединяем две новые точки касания между собой. Это еще один диаметр окружности отличный от найденного в п.3.
6. Точка пересечения двух диаметров будет центром окружности.
0
А, кстати, можно ли одной линейкой построить касательную в данной точке (за конечное время)? Здесь фокус с конусом уже не помешает.
0
Считаю, что если мы оперируем бесконечной линейкой, то нет никаких проблем построить касательную.
0
Опустить касательную из точки, лежащей вне окружности, легко — делается за 9 прямых (две последние — касательные). А вот если точка на окружности — пока глухо.
0
А очень интересный вопрос, кстати. Проективным свойствам такое построение вроде как не противоречит
Отличный ответ, например: otvet.mail.ru/question/51786724
Отличный ответ, например: otvet.mail.ru/question/51786724
0
Ответ пока не смотрел. Получилось за 7 прямых (с помощью теоремы Паскаля).
UPD. Посмотрел ответ. Шутники :)
UPD. Посмотрел ответ. Шутники :)
0
Я уж и забыл, что такая теорема есть)
0
А можно поподробнее? Как все-таки провести касательную?
0
А все я понял. Надо теорему паскаля применить, когда одна сторона шестиугольника вырождается в точку.
0
Выходит, можно найти центр? Доказательство неверное?
-1
Нет, точно и за конечное число операций его найти нельзя.
Но доказательство не совсем верное: в нём не учитывается, что мы можем посмотреть, с какой стороны от данной точки пересеклись две прямые, и действовать в зависимости от результата. Хотя, наверное, подправить доказательство было бы несложно.
Но доказательство не совсем верное: в нём не учитывается, что мы можем посмотреть, с какой стороны от данной точки пересеклись две прямые, и действовать в зависимости от результата. Хотя, наверное, подправить доказательство было бы несложно.
0
А можно поподробнее? Что означает, с какой стороны?
0
Ну, например, построили мы прямую A, которая пересекает окружность. Потом в какой то момент у нас появилась прямая B, пересекающаяся с А в точке Х, лежащей вне окружности. И для дальнейшей работы нам почему-то понадобилась точка Y на прямой A, лежащая между X и ближайшей к ней точкой пересечения A с окружностью. Или сама ближайшая точка пересечения.
В этом случае мы можем с удивлением обнаружить, что тень точки Y оказалась не с той стороны от окружности или от тени точки X (и объявить, что именно из-за этого «тень алгоритма» дала неверный результат :D ). Проблема в том, что проективные преобразования не сохраняют линейного порядка точек на прямой.
В этом случае мы можем с удивлением обнаружить, что тень точки Y оказалась не с той стороны от окружности или от тени точки X (и объявить, что именно из-за этого «тень алгоритма» дала неверный результат :D ). Проблема в том, что проективные преобразования не сохраняют линейного порядка точек на прямой.
+3
Спасибо за наводку на интересную тонкость, про которую я никогда не задумывался. Действительно на «верхней» плоскости есть одна выделенная прямая, тень от которой не попадает в «нижнюю» плоскость. И эта прямая делит плоскость на две полуплоскости, в каждой из которых по-отдельности линейный порядок точек сохраняется.
Чтобы обойти эту трудность, нужно сделать так.
Давайте применим наш чудо-алгоритм на плоскости. Все получившиеся точки пересечений прямых лежат в какой-то ограниченной области. Мы всегда можем подобрать параметры конуса (параметры проективного преобразования) так, что эта ограниченная область будет находится строго в одной из полуплоскостей. Значит линейный порядок точек пересечений будет сохранятся.
Чтобы обойти эту трудность, нужно сделать так.
Давайте применим наш чудо-алгоритм на плоскости. Все получившиеся точки пересечений прямых лежат в какой-то ограниченной области. Мы всегда можем подобрать параметры конуса (параметры проективного преобразования) так, что эта ограниченная область будет находится строго в одной из полуплоскостей. Значит линейный порядок точек пересечений будет сохранятся.
0
del
0
Решение задачи с окружностью.
Воспользуемся тем, что линейка бесконечно длинная.
Выбираем точку, бесконечно отстоящую от окружности, проводим две касательные из этой точки. Точки касания соединяем, образуется первый диаметр. Аналогично проводим две касательные из второй бесконечно удалённой точки. Получаем второй диаметр. Пересечение диаметров — центр.
Убирая требование бесконечной удалённости, можно получить центр с любой заданной точностью, при увеличении расстояния центр будет сходиться). Интересно, как себя поведёт центр-двойник на проекции :)
Воспользуемся тем, что линейка бесконечно длинная.
Выбираем точку, бесконечно отстоящую от окружности, проводим две касательные из этой точки. Точки касания соединяем, образуется первый диаметр. Аналогично проводим две касательные из второй бесконечно удалённой точки. Получаем второй диаметр. Пересечение диаметров — центр.
Убирая требование бесконечной удалённости, можно получить центр с любой заданной точностью, при увеличении расстояния центр будет сходиться). Интересно, как себя поведёт центр-двойник на проекции :)
+1
Задачи хорошие, но решения как решения, вполне обычные, не вижу в них ничего необычного. После интригующего начала статьи ждал чего-то по-оригинальнее.
+1
Решение первой задачи, на правах шутки:
Берем линейку длиной больше, чем диаметр окружности, проводим прямую, пересекающую окружность в двух точках, затем ломаем линейку пополам, делаем циркуль, а дальше нехитрыми построениями линейкой(одна из ножек циркуля) и циркулем строим прямую перпендикулярную отрезку и проходящую через его середину. Диаметр окружности будет лежать на этом перпендикуляре. А дальше, опять же при помощи линейки и циркуля, находим середину диаметра. Это и будет центр нашей окружности
Берем линейку длиной больше, чем диаметр окружности, проводим прямую, пересекающую окружность в двух точках, затем ломаем линейку пополам, делаем циркуль, а дальше нехитрыми построениями линейкой(одна из ножек циркуля) и циркулем строим прямую перпендикулярную отрезку и проходящую через его середину. Диаметр окружности будет лежать на этом перпендикуляре. А дальше, опять же при помощи линейки и циркуля, находим середину диаметра. Это и будет центр нашей окружности
0
А вот ещё задача с «необычным» решением:
Доказать, что среди всех выпуклых n-угольников с заданными сторонами a1,… an наибольшая площадь будет у того, который вписан в окружность.
Доказать, что среди всех выпуклых n-угольников с заданными сторонами a1,… an наибольшая площадь будет у того, который вписан в окружность.
Доказательство
Нарисуем n-угольник, вписанный в окружность, и саму эту окружность (пусть она будет радиуса R).
Круг, ограниченный окружностью, состоит из одного n-угольника и n сегментов.
Теперь возьмём другой n-угольник с теми же сторонами, и построим на этих сторонах сегменты того же радиуса R. Получится фигура (невыпуклая),
длина границы которой равна 2*pi*R. Поскольку из всех фигур с одинаковой длиной границы наибольшую площадь имеет круг, площадь нашей фигуры меньше площади круга, получившегося для первого многоугольника. А поскольку площади сегментов в обоих случаях одинаковы, площадь второго многоугольника будет меньше площади первого, что и требовалось доказать.

Круг, ограниченный окружностью, состоит из одного n-угольника и n сегментов.
Теперь возьмём другой n-угольник с теми же сторонами, и построим на этих сторонах сегменты того же радиуса R. Получится фигура (невыпуклая),
длина границы которой равна 2*pi*R. Поскольку из всех фигур с одинаковой длиной границы наибольшую площадь имеет круг, площадь нашей фигуры меньше площади круга, получившегося для первого многоугольника. А поскольку площади сегментов в обоих случаях одинаковы, площадь второго многоугольника будет меньше площади первого, что и требовалось доказать.

+3
Мозг за десять лет после последнего появления на матмехе окончательно съёжился, так что тупо втыкал в решения, да и те не все понял =).
Вопрос по доказательству четвёртой задачи: когда автор пишет «Получаем формулу для площади dS тени от доски, которая равна длине тени умноженной на ее ширину» — что он имеет в виду? У dS же форма не прямоугольная. Та граница тени, которая более удалена от центра, очевидно короче чем та граница, что ближе к центру. Соответственно, в развёрнутом на плоскость виде тень будет не прямоугольной, а изогнутой.
Вопрос по доказательству четвёртой задачи: когда автор пишет «Получаем формулу для площади dS тени от доски, которая равна длине тени умноженной на ее ширину» — что он имеет в виду? У dS же форма не прямоугольная. Та граница тени, которая более удалена от центра, очевидно короче чем та граница, что ближе к центру. Соответственно, в развёрнутом на плоскость виде тень будет не прямоугольной, а изогнутой.
+2
у dS такая форма, что ее можно развернуть в полоску постоянной ширины dx/cos(phi).
0
Прекрасно. Но что у этой полоски будет являться длиной? Длина одной из дуг на сфере? Если так, то площадь этой полоски вряд ли может считаться по формуле, справедливой для прямоугольников.
0
Но что у этой полоски будет являться длиной? Длина одной из дуг на сфере?
Да
площадь этой полоски вряд ли может считаться по формуле, справедливой для прямоугольников.
Можно считать. Надо просто полоску мысленно разделить на очень много маленьких прямоугольников, для которых формула верна. Потом просуммировать. Получится написанная выше формула.
0
Это как минимум неочевидно.
Коль уж две из четырёх задач (про метро и про колодец) требуют предъявления строгого доказательства вещей, которые большинство людей считает очевидными, то использовать в доказательствах утверждения, таковыми не являющиеся и требующие как минимум дополнительного доказательства — может и корректно с точки зрения профессионального математика, для которого «порог очевидности» явно выше, но не очень этично по отношению к более среднестатистическому читателю.
А то получается как в том посте про доказательство-парадокс: оно вроде и написано, но для его осознание требуется углубляться в отдельные его шаги и уже их либо доказывать самостоятельно, либо тупо принимать на веру.
Кстати. Вот вы, как я понимаю, имеете достаточно близкие отношения с математикой, я читал ваш пост про подделку подписей шарнирным механизмом — и это было впечатляюще.
Но дело не в этом. Вы можете рассказать, есть ли в профессиональном математическом сообществе некие «стандарты очевидности» при публикации работ в профильных изданиях? То есть, требуется ли как-то оформлять свою работу так, чтобы читающий не рылся в глубинах своей памяти, пытаясь вспомнить, почему утверждение автора, что из А следует B, истинно, а получал ссылку на использованную в этом месте теорему и мог просто проверить, насколько эта ссылка уместна?
Коль уж две из четырёх задач (про метро и про колодец) требуют предъявления строгого доказательства вещей, которые большинство людей считает очевидными, то использовать в доказательствах утверждения, таковыми не являющиеся и требующие как минимум дополнительного доказательства — может и корректно с точки зрения профессионального математика, для которого «порог очевидности» явно выше, но не очень этично по отношению к более среднестатистическому читателю.
А то получается как в том посте про доказательство-парадокс: оно вроде и написано, но для его осознание требуется углубляться в отдельные его шаги и уже их либо доказывать самостоятельно, либо тупо принимать на веру.
Кстати. Вот вы, как я понимаю, имеете достаточно близкие отношения с математикой, я читал ваш пост про подделку подписей шарнирным механизмом — и это было впечатляюще.
Но дело не в этом. Вы можете рассказать, есть ли в профессиональном математическом сообществе некие «стандарты очевидности» при публикации работ в профильных изданиях? То есть, требуется ли как-то оформлять свою работу так, чтобы читающий не рылся в глубинах своей памяти, пытаясь вспомнить, почему утверждение автора, что из А следует B, истинно, а получал ссылку на использованную в этом месте теорему и мог просто проверить, насколько эта ссылка уместна?
0
Спасибо за шарниры)
Вы правы в том, что человек, который хочет написать так, чтобы его поняли, должен предвидеть все неочевидные для читателя места. Но он, одновременно с этим, не должен очень сильно вдаваться в детали, иначе текст очень просто превратиться в занудную скучность. Я очень старался держаться золотой середины. В каких-то местах это получилось, в каких-то, как я вижу по комментам, не совсем. Но я, все-равно, до сих считаю, что расписывать подробнее про площадь — излишне. Может быть следовало больше внимания уделить первой задаче про конус, которая вызвала очень много дискуссий.
А насчет профессиональных статей по математике. Они написаны обычно так, что статью может сразу понять только математик работающий именнов в этой тематике. Грамотному математику из другой области нужно будет очень много времени, чтобы полностью разобраться в статье. Чтобы ее понять, ему придется еще изучить штук 10 других статей.
Вы правы в том, что человек, который хочет написать так, чтобы его поняли, должен предвидеть все неочевидные для читателя места. Но он, одновременно с этим, не должен очень сильно вдаваться в детали, иначе текст очень просто превратиться в занудную скучность. Я очень старался держаться золотой середины. В каких-то местах это получилось, в каких-то, как я вижу по комментам, не совсем. Но я, все-равно, до сих считаю, что расписывать подробнее про площадь — излишне. Может быть следовало больше внимания уделить первой задаче про конус, которая вызвала очень много дискуссий.
А насчет профессиональных статей по математике. Они написаны обычно так, что статью может сразу понять только математик работающий именнов в этой тематике. Грамотному математику из другой области нужно будет очень много времени, чтобы полностью разобраться в статье. Чтобы ее понять, ему придется еще изучить штук 10 других статей.
0
Я вот не понимаю почему не принимается в качестве доказательств повседневная логика в математических или геометрических абстракциях. Вот пример:
Окружность и линейка.
Окружность определяется радиусом и центром. Окружность имеет угол (360 вечно ваш КО). Чтобы найти угол линейка не подходит. Доказано.
Задача московского метро.
Это просто определяется евклидовой метрикой пространства. Можно с точностью до индукции упростить до одномерного случая.
Кирпичная стена.
Ряд который рано или поздно сойдется в среднем по ансамблю. Играйте в тетрис, короче.
Задача про колодец.
Мое любимое. Вот ты смотри, берешь доску перекрываешь дыру, и на нее кладешь следующую. Не-ет, лучше рядом, так ты просто перекрываешь часть уже занятую другой доской. Оптимальное решение класть другую доску рядом. Так, так — ну точно не меньше.
Окружность и линейка.
Окружность определяется радиусом и центром. Окружность имеет угол (360 вечно ваш КО). Чтобы найти угол линейка не подходит. Доказано.
Задача московского метро.
Это просто определяется евклидовой метрикой пространства. Можно с точностью до индукции упростить до одномерного случая.
Кирпичная стена.
Ряд который рано или поздно сойдется в среднем по ансамблю. Играйте в тетрис, короче.
Задача про колодец.
Мое любимое. Вот ты смотри, берешь доску перекрываешь дыру, и на нее кладешь следующую. Не-ет, лучше рядом, так ты просто перекрываешь часть уже занятую другой доской. Оптимальное решение класть другую доску рядом. Так, так — ну точно не меньше.
-2
Ещё решение первой задачи.
С точки зрения бесконечной линейки, можно использовать её ширину, для построения n-ного количества равноотстоящих точек на окружности, после чего разделить чётное количество (у нечётного отнять 1 и разделить) на 2 и соединить парные точки отрезками. Каждый цикл в 360 градусов, будет создавать набор точек. Продолжать накладывать точки пока первая и последняя не совпадут. С получившимся набором центральных точек, которые создадут гораздо более маленький круг, делать то же самое. Продолжать рекурсивно до получения одной точки.
С точки зрения бесконечной линейки, можно использовать её ширину, для построения n-ного количества равноотстоящих точек на окружности, после чего разделить чётное количество (у нечётного отнять 1 и разделить) на 2 и соединить парные точки отрезками. Каждый цикл в 360 градусов, будет создавать набор точек. Продолжать накладывать точки пока первая и последняя не совпадут. С получившимся набором центральных точек, которые создадут гораздо более маленький круг, делать то же самое. Продолжать рекурсивно до получения одной точки.
0
К сожалению, линейка — это прямая, без ширины. Если бы у нас была линейка постоянной ширины с параллельными краями, да ещё и была бы разрешена операция «приложить линейку к плоскости так, чтобы одна сторона проходила через одну заданную точку, а другая — через другую», то с помощью такой линейки можно выполнить любое построение, которое выполняется с помощью циркуля и бесконечно тонкой линейки.
Например, найти центр окружности с помощью линейки, ширина которой меньше диаметра окружности, можно за 9 операций:
— пересекли окружность парой параллельных прямых, проходящих на разных расстояниях от центра. Точки пересечения с окружностью — вершины равносторонней трапеции (или равнобочной?)
— построили у трапеции точку пересечения боковых сторон и точку пересечения диагоналей. Соединили — получили диаметр.
— провели две пары параллельных прямых, проходящих через концы диаметра. Получился ромб.
— Провели у ромба вторую диагональ. Она пересекла первую в центре окружности.
Например, найти центр окружности с помощью линейки, ширина которой меньше диаметра окружности, можно за 9 операций:
— пересекли окружность парой параллельных прямых, проходящих на разных расстояниях от центра. Точки пересечения с окружностью — вершины равносторонней трапеции (или равнобочной?)
— построили у трапеции точку пересечения боковых сторон и точку пересечения диагоналей. Соединили — получили диаметр.
— провели две пары параллельных прямых, проходящих через концы диаметра. Получился ромб.
— Провели у ромба вторую диагональ. Она пересекла первую в центре окружности.
+1
Вспомнился забавный случай, произошедший со мной, когда я лежал на 23-е февраля n-го года в больнице на Соколиной горе в Москве. Врачей в это время не было, были только медсестры, по случаю праздника. Поэтому лежать приходилось до окончания выходных. Делать было нечего, поэтому я готовился к студенческой математической олимпиаде.
В палате со мной лежал какой-то бывший заключенный, солдат (то ли бывший, то ли нет) и еще какой-то мутный парень. Суть в том, что они быстренько сообразили спирта у медсестер, нашинковали апельсинчики и приготовились отмечать «настоящий мужской праздник».
Мне было не очень интересно, я провалялся весь день под капельницей, поэтому спокойно решал олимпиадные задачки прошлых лет. Ну и вот, «уголовник» подошел ко мне со стаканом спирта и долькой апельсина и говорит: «ну че, ты как не родной, давай присоединяйся, чем ты тут занимаешься?». Я вежливо ему ответил, что занимаюсь подготовкой к олимпиаде, мол, математик я. И тогда он меня попросил показать какой-нибудь математической фокус, чтобы спорить с людьми на деньги.
Я ему предложил такой вариант: я могу доказать, что любое число равно нулю. «О! это супер! на это любой поведется! Давай учи меня» — радостно воскликнул он. Мое доказательство было такое:
Есть интеграл:
 ,
,
который мы постараемся взять по частям заменой
}=u,&space;cos(x)dx=dv)
Тогда
}{sin^2(x)}dx,&space;v&space;=&space;sin(x))
повторяя последовательное взятие по частям получим цепочку
}sin(x)+\int\frac{cos(x)sin(x)}{sin^2(x)}dx=1+\int\frac{cos(x)}{sin(x)}dx=2+\int\frac{cos(x)}{sin(x)}dx=...=n+\int\frac{cos(x)}{sin(x)}dx)
Т.е. 0=1=2=...=n
Ну, конечно, пришлось еще объяснить что такое интеграл.
В палате со мной лежал какой-то бывший заключенный, солдат (то ли бывший, то ли нет) и еще какой-то мутный парень. Суть в том, что они быстренько сообразили спирта у медсестер, нашинковали апельсинчики и приготовились отмечать «настоящий мужской праздник».
Мне было не очень интересно, я провалялся весь день под капельницей, поэтому спокойно решал олимпиадные задачки прошлых лет. Ну и вот, «уголовник» подошел ко мне со стаканом спирта и долькой апельсина и говорит: «ну че, ты как не родной, давай присоединяйся, чем ты тут занимаешься?». Я вежливо ему ответил, что занимаюсь подготовкой к олимпиаде, мол, математик я. И тогда он меня попросил показать какой-нибудь математической фокус, чтобы спорить с людьми на деньги.
Я ему предложил такой вариант: я могу доказать, что любое число равно нулю. «О! это супер! на это любой поведется! Давай учи меня» — радостно воскликнул он. Мое доказательство было такое:
Есть интеграл:
 ,
,который мы постараемся взять по частям заменой
Тогда
повторяя последовательное взятие по частям получим цепочку
}sin(x)+\int\frac{cos(x)sin(x)}{sin^2(x)}dx=1+\int\frac{cos(x)}{sin(x)}dx=2+\int\frac{cos(x)}{sin(x)}dx=...=n+\int\frac{cos(x)}{sin(x)}dx)
Т.е. 0=1=2=...=n
Ну, конечно, пришлось еще объяснить что такое интеграл.
+1
Спасибо за красивый парадокс. Кстати можно точно такой же парадокс сделать и с интегралом 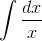
Ну а ключ к разгадке в том, что неопределенный интеграл определен с точностью до константы.
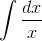
Ну а ключ к разгадке в том, что неопределенный интеграл определен с точностью до константы.
0
Слишком длинное доказательство на «Задачу московского метро».
Я вижу так:
Есть ящик a * b * c, кладём его в ящик a' * b' * c'
Если 'a < a, то не сможем положить => a' >= a, аналогично, b' > b, c' > c => a' + b' + c' >= a + b + c
«Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше 150 см, в ящик с суммой измерений меньше 150 см.»
Если a + b + c > 150 => a' + b' + c' > 150, ч.т.д.
Я вижу так:
Есть ящик a * b * c, кладём его в ящик a' * b' * c'
Если 'a < a, то не сможем положить => a' >= a, аналогично, b' > b, c' > c => a' + b' + c' >= a + b + c
«Доказать, что нельзя обмануть систему и полностью засунуть ящик, сумма измерений которого больше 150 см, в ящик с суммой измерений меньше 150 см.»
Если a + b + c > 150 => a' + b' + c' > 150, ч.т.д.
-1
А верно ли, что если в R2(Rn) одна область содержится в другой, обе выпуклые и ограниченные, то граница у внутренней области меньше?
0
В R2 верно — работает тот же приём с раздуванием. В Rn уже не очень очевидно.
0
Нет, в Rn, скорее всего, тоже верно. Приблизим поверхность симплексами (например, взяв выпуклую оболочку достаточно плотного множества точек на поверхности), над каждым симплексом построим полубесконечную прямую призму. Эти призмы не пересекаются (из выпуклости), вторая поверхность пересекает каждую из призм, и гиперплощадь пересечения больше гиперплощади самого симплекса. Надо только доказать, что внутреннюю поверхность можно приблизить сколь угодно точно по гиперплощади.
0
Вспомнился афоризм
For every phenomenon, however complex, someone will eventually come up with a simple and elegant theory. This theory will be wrong.
+1
Sign up to leave a comment.
Задачи с красивыми решениями