Требуемые знания: знакомство с методами линейной бинарной классификации (e.g. SVM (см. SVM Tutorial)), линейная алгебра, линейное программирование
Рассмотрим линейную задачу бинарной классификации (если задача линейно неразделима, её можно свести к таковой с помощью симметричного интегрального L-2 ядра(см. SVM)). При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».
При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».
В своей статье я хочу для начала провести краткий обзор метода из этой статьи Gene_Selection_for_Cancer_Classification_using, после чего предложить свой метод.
Основная идея метода понижения размерности в Gene_Selection_for_Cancer_Classification_using заключается в ранжировании всех компонент. Предлагается следующий алгоритм:
В основном в статье расматривается способ присвоения весов полученных SVM.То есть используем в качестве весов коэффициенты в классифицирующей функции соответствующих компонент. Допустим после тренировки SVM мы получили классифицирующую функцию (w,x) + b=0, тогда wi компонент будет весом компоненты i. Также в статье рассматривается корреляционный способ задания весов, но он, как и любой другой, проигрывает SVM способу, т.к. при повторном попадании на шаг 1 весовые коэффициенты в SVM способе известны из шага 3.
Класс таких алгоритмов по-прежнему вынужден тренировать SVM на образцах большой размерности, т.е. проблемы погрешности и скорости не решаются. Всё что он даёт — это возможность после тренировки SVM сократить число компонент классифицируемых образцов. Если опытное получение значений сокращённых компонент финансово затратно, то можно сэкономить.
P.S. Кроме того выбор весов как wi довольно спорный. Я бы предложил хотя бы домножить их на выборочную дисперсию компоненты i по всем образцам или на первый центральный абсолютный выборочный момент компоненты i по всем образцам.
Идея такова: выбрасываем компоненту и проверяем будет ли теперь (без этой компоненты) множество образцов линейно разделимо. Если да, то не возвращаем эту компоненту, если нет то возвращаем. Вопрос в том как проверить множество на линейную разделимость?
Пусть xi — образцы, yi — принадлежность образца к классу (yi=-1 — первый класс, yi=1 — второй класс) i=1..m. Тогда образцы линейно разделимы, если — имеет нетривиальное решение, где
— имеет нетривиальное решение, где  (условия как при тренировке SVM).
(условия как при тренировке SVM).
_____________________________________________________________________________________
Давайте для начала рассмотрим как можно проверить множество на строгую линейную разделимость:
 — имеет решение. По лемме Фаркаша <=>
— имеет решение. По лемме Фаркаша <=> 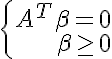 — имеет только тривиальное решение. Проверяем вектор 0 на оптимальность в задаче линейного программирования с полученными ограничениями и целевой функцией
— имеет только тривиальное решение. Проверяем вектор 0 на оптимальность в задаче линейного программирования с полученными ограничениями и целевой функцией 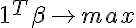 Если 0 оказался оптимальным, значит множество строго линейно разделимо.
Если 0 оказался оптимальным, значит множество строго линейно разделимо.
_____________________________________________________________________________________
Нестрогая линейная разделимость:
 — имеет нетривиальное решение. По лемме Фаркаша <=>
— имеет нетривиальное решение. По лемме Фаркаша <=> 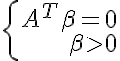 — не имеет решений. <=>
— не имеет решений. <=>  — не имеет решений. Для проверки наличия решения полученных ограничений можно использовать любой метод нахождения начального опорного вектора в задаче линейного программирования с данными ограничениями.
— не имеет решений. Для проверки наличия решения полученных ограничений можно использовать любой метод нахождения начального опорного вектора в задаче линейного программирования с данными ограничениями.
_____________________________________________________________________________________
В некоторых задачах (особенно когда размерность (n) превышает число образцов (m)) мы можем захотеть отбрасывать компоненту только если разделение множества происходит с некоторым зазором. Тогда можно проверять такие условия: — имеет решение, где c>=0 параметр зазора, а второе ограничение заменяет нормировку альфа(чтобы нельзя было решение A*x>0 просто умножить на достаточно большую константу k и удовлетворить системе A*k*x>=c). Эти условия по лемме Фаркаша(E — единичная матрица) <=>
— имеет решение, где c>=0 параметр зазора, а второе ограничение заменяет нормировку альфа(чтобы нельзя было решение A*x>0 просто умножить на достаточно большую константу k и удовлетворить системе A*k*x>=c). Эти условия по лемме Фаркаша(E — единичная матрица) <=> 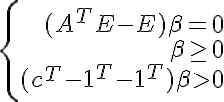 — не имеет решений. Проверяем вектор 0 на оптимальность в задаче линейного программирования с полученными ограничениями(без последней строчки) и целевой функцией
— не имеет решений. Проверяем вектор 0 на оптимальность в задаче линейного программирования с полученными ограничениями(без последней строчки) и целевой функцией 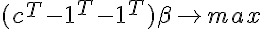 Если 0 оказался оптимальным, значит множество можно разделить с заданным зазором.
Если 0 оказался оптимальным, значит множество можно разделить с заданным зазором.
_____________________________________________________________________________________
В некоторых задачах (особенно когда число образцов (m) превышает размерность (n)) мы можем захотеть отбрасывать компоненту даже если разделение множества происходит с некоторой ошибкой. Тогда можно проверять такие условия: — имеет решение, где c<=0 параметр ошибки, а вторые ограничения заменяют нормировку альфа (чтобы нельзя было решение A*x>negative_number_less_than_c просто разделить на достаточно большую константу k и удовлетворить системе A*x/k>=c). Здесь всё аналогично вышеописанному случаю, только из-за дизъюнкции(квадратной скобки) придётся рассмотреть две задачи линейного программирования.
— имеет решение, где c<=0 параметр ошибки, а вторые ограничения заменяют нормировку альфа (чтобы нельзя было решение A*x>negative_number_less_than_c просто разделить на достаточно большую константу k и удовлетворить системе A*x/k>=c). Здесь всё аналогично вышеописанному случаю, только из-за дизъюнкции(квадратной скобки) придётся рассмотреть две задачи линейного программирования.
Рассмотрим линейную задачу бинарной классификации (если задача линейно неразделима, её можно свести к таковой с помощью симметричного интегрального L-2 ядра(см. SVM)).
 При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».
При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».В своей статье я хочу для начала провести краткий обзор метода из этой статьи Gene_Selection_for_Cancer_Classification_using, после чего предложить свой метод.
Алгоритмы из Gene_Selection_for_Cancer_Classification_using
Основная идея метода понижения размерности в Gene_Selection_for_Cancer_Classification_using заключается в ранжировании всех компонент. Предлагается следующий алгоритм:
- Присваиваем всем(оставшимся) компонентам некоторые весовые коэффициенты (о том как — далее)
- Выкидываем компоненту с минимальным весом из всех образцов.
- Тренируем SVM. Если не удалось разделить образцы, то возвращаем выкинутую на прошлом шаге компоненту и выходим из алгоритма, в противном случае переходим на шаг 1 с данными без выкинутой компоненты.
В основном в статье расматривается способ присвоения весов полученных SVM.То есть используем в качестве весов коэффициенты в классифицирующей функции соответствующих компонент. Допустим после тренировки SVM мы получили классифицирующую функцию (w,x) + b=0, тогда wi компонент будет весом компоненты i. Также в статье рассматривается корреляционный способ задания весов, но он, как и любой другой, проигрывает SVM способу, т.к. при повторном попадании на шаг 1 весовые коэффициенты в SVM способе известны из шага 3.
Класс таких алгоритмов по-прежнему вынужден тренировать SVM на образцах большой размерности, т.е. проблемы погрешности и скорости не решаются. Всё что он даёт — это возможность после тренировки SVM сократить число компонент классифицируемых образцов. Если опытное получение значений сокращённых компонент финансово затратно, то можно сэкономить.
P.S. Кроме того выбор весов как wi довольно спорный. Я бы предложил хотя бы домножить их на выборочную дисперсию компоненты i по всем образцам или на первый центральный абсолютный выборочный момент компоненты i по всем образцам.
Мой алгоритм
Идея такова: выбрасываем компоненту и проверяем будет ли теперь (без этой компоненты) множество образцов линейно разделимо. Если да, то не возвращаем эту компоненту, если нет то возвращаем. Вопрос в том как проверить множество на линейную разделимость?
Пусть xi — образцы, yi — принадлежность образца к классу (yi=-1 — первый класс, yi=1 — второй класс) i=1..m. Тогда образцы линейно разделимы, если


_____________________________________________________________________________________
Давайте для начала рассмотрим как можно проверить множество на строгую линейную разделимость:

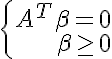
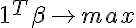
_____________________________________________________________________________________
Нестрогая линейная разделимость:

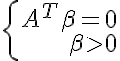

_____________________________________________________________________________________
В некоторых задачах (особенно когда размерность (n) превышает число образцов (m)) мы можем захотеть отбрасывать компоненту только если разделение множества происходит с некоторым зазором. Тогда можно проверять такие условия:

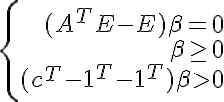
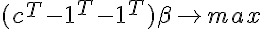
_____________________________________________________________________________________
В некоторых задачах (особенно когда число образцов (m) превышает размерность (n)) мы можем захотеть отбрасывать компоненту даже если разделение множества происходит с некоторой ошибкой. Тогда можно проверять такие условия:
