Прочитав недавно статью «Введение в оптимизацию. Имитация отжига» захотел принять участие в сравнении алгоритмов оптимизации. Но ведь их действительно хорошо бы сравнить. А в материалах исходной статьи не приводится никаких количественных данных. Значит, подумал я, надо сначала сформулировать критерии сравнения. Чем и предлагаю заняться в данной статье.
Итак, по каким критериям можно сравнить алгоритмы аналогичные «имитации отжига»? Чаще всего сравнивают:
• эффективность
• скорость работы
• использование памяти
И хотелось бы ещё добавить
• повторяемость (То есть проверить, насколько стабилен алгоритм в получаемых результатах).
В качестве первого критерия будем использовать длину получившегося маршрута. Понятия не имею, каков самый лучший маршрут на случайно сгенерированном наборе точек. Что делать? Попробуем, для простоты, всё прогонять на одном наборе. Более педантичные, для большей достоверности результатов, могут потом расширить на несколько наборов и усреднить результаты. А пока надо добавить считывание тестового набора из файла для возможности повторения эксперимента.
Для определения скорости работы посчитаем затраченное процессором на алгоритм время, благо есть в Octave такая функция. Конечно на разных компьютерах результат будет тоже разным. Поэтому можно для сравнения все результаты масштабировать по какому либо одному алгоритму, прогоняемому всегда. Например, по алгоритму из исходной статьи, раз уж он попался первым.
По расходу памяти сходу ничего не придумалось. Поэтому попробуем прикинуть на пальцах. Насколько я понял, основные расходы у автора — это два массива индексов. Один для текущего маршрута, другой — для маршрута-кандидата. Ну и, конечно, массив точек маршрута по две координаты на точку. Остальные расходы учитывать не будем, так как они будут разные в разных средах выполнения и не зависят от размера тестовых данных. (Возможно здесь я несколько резок, но вполне открыт для предложений). Итого основные расходы N*4, где N — количество точек которые надо обойти.
Небольшое отступление: всё описанное здесь проверялось не в MatLab, как в оригинальной статье, а в Octave [http://www.gnu.org/software/octave/]. Причин тому несколько — во-первых, она у меня есть, во-вторых, её язык программирования почти полностью совмести с MatLab, ну и наконец, она может быть у каждого ибо бесплатна и общедоступна.
Для начала убеждаемся в совместимости для имеющегося кода (скачивается по ссылке в конце исходной статьи). Всё работает, но оказывается, что там нет кода генерирующего приводимые в ней красивые графики. Не беда — напишем свою функцию из которой вызываем оригинальный алгоритм и рисуем результат. Всё равно она понадобится для обвеса всего сбором статистики.
Итак функция Analyze:
Функцию для генерации файла с массивом координат городов писать не стал. Сделать это можно прямо из командной строки:
Да, если кто заметил, что для оценки не используется функция CalculateEnergy из исходного алгоритма, то тому есть две причины. Во-первых, есть мысль попробовать работу на других метриках, а результат лучше всё же оценивать евклидовым расстоянием. А во-вторых, хотя автор исходной статьи и описал подробно вычисление евклидова расстояния, код в исходниках вычисляет манхэттенское. Евклидово для двух точек правильно вычислять так:
Ну и, чтобы определить насколько результат стабилен от раза к разу, будем запускать всё это в цикле много раз, собирать результаты и оценивать их среднее и степень разброса результатов:
Первое разочарование — как всё долго! На компьютере core i5-3450 3.1GHz 8Gb ОЗУ один проход выполняется в среднем 578 секунд. Так хотелось для пущей достоверности запустить и усреднить 1000 циклов но это… 6.69 суток. Пришлось запустить на 100 циклов и через примерно 16 часов 4 минуты (то есть наутро) имеем результат:
среднее время вычисления 578.1926 (стандартное отклонение в выборке 3.056), средняя длина получившегося пути 91.0844 (стандартное отклонение 2.49). То есть всё более чем стабильно, а, следовательно, пригодно к использованию. Но как же долго. Не удержался и соблазнился заняться оптимизацией.
Первый кандидат для ускорения — оценка расстояния. Octave, как и MatLab оптимизированы для матричных вычислений — под это и перепишем. Функция будет принимать два массива: A — начала отрезков, B — их концы соответственно:
Чтобы вызвать эту функцию введём ещё одну, которая подготовит данные, циклически сдвинув исходный массив точек для получения массива концов отрезков:
Ну и, конечно, надо переписать функцию SimulatedAnnealing и GenerateStateCandidate для работы непосредственно с массивами точек. Полный код приводить не буду, в конце будет ссылка на архив со всеми исходниками для тех, кому интересно.
Запускаем, смотрим… среднее время вычисления 70.554 (стандартное отклонение в выборке 0.096), средняя длина получившегося пути 90.403 (стандартное отклонение 2.204).
Прирост скорости более чем в восемь раз! Дальше стараться уже и не интересно — такого прироста уже не получить. Правда расход памяти (по предложенной методике) теперь два массива точек по две координаты (текущее решение и новый кандидат), то есть … N*4. Ничего не изменилось.
Но, раз уж оценивать алгоритм, проверим данные температур. Исходная «энергия» сгенерированных массивов точек колеблется около 500 — 700 итоговые маршруты на выходе колеблются около 90 плюс/минус 5. Следовательно выбранные автором температуры практически обеспечивают только ограничение в 100000 итераций (кстати, оно также и жёстко забито в коде. Для предотвращения зацикливания, наверное. Я поднял до десяти миллионов, зачем себя сдерживать при проверке алгоритма?). И действительно, немного поэкспериментировав получаем примерно те же результаты для Tmax=300 и Tmin=0.001. При этом время выполнения сократилось до 21 секунды.
Теперь попробуем сравнить с чем-нибудь. Изначально была идея сравнить с манхэттенской метрикой, но оказалось, что она и была реализована. Потом ещё эта оптимизация. Короче — добавляем код для матричного расчёта манхэттенского расстояния и пробуем для него. Так же интересно как покажет себя другая функция изменения температуры. Тех, кто обманулся обещанной в исходной статье линейностью функции изменения температуры, вынужден разочаровать — она таковой не является. Чтобы это понять достаточно посмотреть на её график:

Наверное имелась ввиду линейность знаменателя функции, ибо знаменатели всех остальных используемых в науке вариантов действительно выглядят страшнее.
Для сравнения попробуем ещё функцию температуры T = Tmax*(A^k) где A выбирается, обычно, в пределах 0.7 — 0.999. (При реализации она вообще не жадная — Ti=A*Ti-1). Варианты «отжига» с её использованием называются «тушением». Она значительно быстрее падает до минимальной температуры, но более пологая на начальном этапе. То есть, с ней алгоритм больше экспериментирует вначале, но быстрее заканчивает работу. Итак — сводная таблица результатов:
Обещанные исходники можно найти по ссылке
Ну и если понравилось — можно через какое-то время сравнить с ещё чем-нибудь.

Итак, по каким критериям можно сравнить алгоритмы аналогичные «имитации отжига»? Чаще всего сравнивают:
• эффективность
• скорость работы
• использование памяти
И хотелось бы ещё добавить
• повторяемость (То есть проверить, насколько стабилен алгоритм в получаемых результатах).
Критерии оценки
В качестве первого критерия будем использовать длину получившегося маршрута. Понятия не имею, каков самый лучший маршрут на случайно сгенерированном наборе точек. Что делать? Попробуем, для простоты, всё прогонять на одном наборе. Более педантичные, для большей достоверности результатов, могут потом расширить на несколько наборов и усреднить результаты. А пока надо добавить считывание тестового набора из файла для возможности повторения эксперимента.
Для определения скорости работы посчитаем затраченное процессором на алгоритм время, благо есть в Octave такая функция. Конечно на разных компьютерах результат будет тоже разным. Поэтому можно для сравнения все результаты масштабировать по какому либо одному алгоритму, прогоняемому всегда. Например, по алгоритму из исходной статьи, раз уж он попался первым.
По расходу памяти сходу ничего не придумалось. Поэтому попробуем прикинуть на пальцах. Насколько я понял, основные расходы у автора — это два массива индексов. Один для текущего маршрута, другой — для маршрута-кандидата. Ну и, конечно, массив точек маршрута по две координаты на точку. Остальные расходы учитывать не будем, так как они будут разные в разных средах выполнения и не зависят от размера тестовых данных. (Возможно здесь я несколько резок, но вполне открыт для предложений). Итого основные расходы N*4, где N — количество точек которые надо обойти.
Небольшое отступление: всё описанное здесь проверялось не в MatLab, как в оригинальной статье, а в Octave [http://www.gnu.org/software/octave/]. Причин тому несколько — во-первых, она у меня есть, во-вторых, её язык программирования почти полностью совмести с MatLab, ну и наконец, она может быть у каждого ибо бесплатна и общедоступна.
Анализируем...
Для начала убеждаемся в совместимости для имеющегося кода (скачивается по ссылке в конце исходной статьи). Всё работает, но оказывается, что там нет кода генерирующего приводимые в ней красивые графики. Не беда — напишем свою функцию из которой вызываем оригинальный алгоритм и рисуем результат. Всё равно она понадобится для обвеса всего сбором статистики.
Итак функция Analyze:
function [timeUsed, distTotal] = Analyze( )
% считывание массива городов из файла для повторяемости результата
load points_data.dat cities
% засечка времени выполнения
timeStart = cputime();
% собственно поиск маршрута
result = SimulatedAnnealing(cities, 10, 0.00001);
% определение затраченного процессором времени
timeUsed = cputime - timeStart;
% вычисление общей длины маршрута
distTotal = PathLengthMat(result);
% рисование итогового маршрута
plot(result(:,1), result(:,2), '-*');
drawnow ();
end
Функцию для генерации файла с массивом координат городов писать не стал. Сделать это можно прямо из командной строки:
cities = rand(100, 2)*10;
save points_data.dat cities;
Да, если кто заметил, что для оценки не используется функция CalculateEnergy из исходного алгоритма, то тому есть две причины. Во-первых, есть мысль попробовать работу на других метриках, а результат лучше всё же оценивать евклидовым расстоянием. А во-вторых, хотя автор исходной статьи и описал подробно вычисление евклидова расстояния, код в исходниках вычисляет манхэттенское. Евклидово для двух точек правильно вычислять так:
function [dist] = distEuclid(A, B)
dist = (A - B).^2;
dist = sum(dist);
dist = sqrt(dist);
end
Ну и, чтобы определить насколько результат стабилен от раза к разу, будем запускать всё это в цикле много раз, собирать результаты и оценивать их среднее и степень разброса результатов:
function [] = Statistics
testNum = 1000;
% инициализация массивов для сбора статистики
timeUsed = zeros(testNum,1);
distTotal = zeros(testNum,1);
for n=1:testNum
[timeUsed(n), distTotal(n)] = Analyze;
end
% определение средних значений и разброса
time = [mean(timeUsed), std(timeUsed)]
dist = [mean(distTotal), std(distTotal)]
end
Первое разочарование — как всё долго! На компьютере core i5-3450 3.1GHz 8Gb ОЗУ один проход выполняется в среднем 578 секунд. Так хотелось для пущей достоверности запустить и усреднить 1000 циклов но это… 6.69 суток. Пришлось запустить на 100 циклов и через примерно 16 часов 4 минуты (то есть наутро) имеем результат:
среднее время вычисления 578.1926 (стандартное отклонение в выборке 3.056), средняя длина получившегося пути 91.0844 (стандартное отклонение 2.49). То есть всё более чем стабильно, а, следовательно, пригодно к использованию. Но как же долго. Не удержался и соблазнился заняться оптимизацией.
Оптимизация
Первый кандидат для ускорения — оценка расстояния. Octave, как и MatLab оптимизированы для матричных вычислений — под это и перепишем. Функция будет принимать два массива: A — начала отрезков, B — их концы соответственно:
function [dist] = distEuclid(A, B)
dist = (A - B).^2;
dist = sum(dist, 2);
dist = sqrt(dist);
dist = sum(dist);
end
Чтобы вызвать эту функцию введём ещё одну, которая подготовит данные, циклически сдвинув исходный массив точек для получения массива концов отрезков:
function [length] = PathLengthMat(cities)
citiesShifted = circshift(cities, 1);
length = distEuclid(cities, citiesShifted);
end
Ну и, конечно, надо переписать функцию SimulatedAnnealing и GenerateStateCandidate для работы непосредственно с массивами точек. Полный код приводить не буду, в конце будет ссылка на архив со всеми исходниками для тех, кому интересно.
Запускаем, смотрим… среднее время вычисления 70.554 (стандартное отклонение в выборке 0.096), средняя длина получившегося пути 90.403 (стандартное отклонение 2.204).
Прирост скорости более чем в восемь раз! Дальше стараться уже и не интересно — такого прироста уже не получить. Правда расход памяти (по предложенной методике) теперь два массива точек по две координаты (текущее решение и новый кандидат), то есть … N*4. Ничего не изменилось.
Но, раз уж оценивать алгоритм, проверим данные температур. Исходная «энергия» сгенерированных массивов точек колеблется около 500 — 700 итоговые маршруты на выходе колеблются около 90 плюс/минус 5. Следовательно выбранные автором температуры практически обеспечивают только ограничение в 100000 итераций (кстати, оно также и жёстко забито в коде. Для предотвращения зацикливания, наверное. Я поднял до десяти миллионов, зачем себя сдерживать при проверке алгоритма?). И действительно, немного поэкспериментировав получаем примерно те же результаты для Tmax=300 и Tmin=0.001. При этом время выполнения сократилось до 21 секунды.
Исследуем варианты
Теперь попробуем сравнить с чем-нибудь. Изначально была идея сравнить с манхэттенской метрикой, но оказалось, что она и была реализована. Потом ещё эта оптимизация. Короче — добавляем код для матричного расчёта манхэттенского расстояния и пробуем для него. Так же интересно как покажет себя другая функция изменения температуры. Тех, кто обманулся обещанной в исходной статье линейностью функции изменения температуры, вынужден разочаровать — она таковой не является. Чтобы это понять достаточно посмотреть на её график:
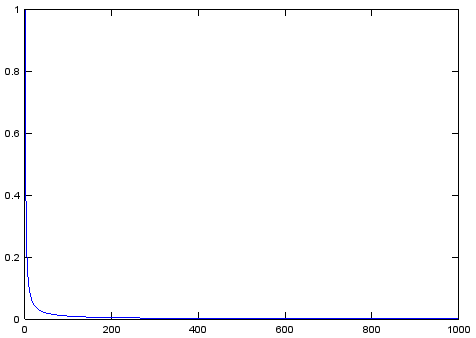
Наверное имелась ввиду линейность знаменателя функции, ибо знаменатели всех остальных используемых в науке вариантов действительно выглядят страшнее.
Для сравнения попробуем ещё функцию температуры T = Tmax*(A^k) где A выбирается, обычно, в пределах 0.7 — 0.999. (При реализации она вообще не жадная — Ti=A*Ti-1). Варианты «отжига» с её использованием называются «тушением». Она значительно быстрее падает до минимальной температуры, но более пологая на начальном этапе. То есть, с ней алгоритм больше экспериментирует вначале, но быстрее заканчивает работу. Итак — сводная таблица результатов:
| Алгоритм | Длина(Разброс) | Время(разброс) | Память |
|---|---|---|---|
| Из статьи | 91.0844 (2.4900) | 578.1926 (3.0560) | N*4 |
| Матричный(10-0.00001) | 90.4037 (2.2038) | 70.554593 (0.096166) | N*4 |
| Матричный(300-0.001) | 90.7956 (2.1967) | 20.94024 (0.16235) | N*4 |
| Матричный манхэттенский(10-0.00001) | 90.0506 (3.2397) | 70.96909 (0.7807) | N*4 |
| Матричный «тушение»(300-0.001) | 92.0963 (2.3129) | 22.59591 (0.39581) | N*4 |
Выводы.
- Возможность количественно оценить результаты работы алгоритма полезная даже если его не с кем сравнивать.
- Если учитывать особенности инструмента при написании программы — можно сэкономить много времени.
- Если подобрать параметры под конкретную задачу — можно сэкономить ещё немного.
- Сравнивать алгоритмы по скорости без оптимизации бессмысленно — время выполнения будет почти случайной величиной.
- Для современных процессоров возвести в степень и извлечь корень почти так же просто, как и взять модуль — можно не извращаться и писать математику почти без упрощений.
- Многие вариации одного алгоритма дают очень близкие результаты, если не графоман — используй что удобнее (или привычнее).
Обещанные исходники можно найти по ссылке
Ну и если понравилось — можно через какое-то время сравнить с ещё чем-нибудь.