Данная статья посвящается светлой памяти моего учителя, доктора технических наук, профессора Кабелькова Александра Николаевича, основателя и первого декана Физико-математического факультета ЮРГТУ (НПИ)
Данное видео иллюстрирует повторный эксперимент — вместо «барашка» используется какая-то самодельная ерунда
Это случилось в 1985 году, на орбитальной станции «Салют-7», во время посещения её экипажем корабля «Союз Т-13» в составе космонавтов Джанибекова В. А. и Савиных В. П. Не буду описывать своими словами, процитировав один из многочисленных сетевых источников
Думаю, что для затравки этого вполне достаточно. На самом деле, в «эффекте Джанибекова» нет ничего экстраординарного (хотя ему причисляют и возможную смену полюсов Земли каждые 12000 лет, и прочие глобальные катаклизмы). Используя аппарат тензорной алгебры и теорию устойчивости механического движения, попробуем разобраться, что происходит с загадочной гайкой.
На рисунке изображен объект нашего исследования. Наверняка каждый из читателей видел такую гайку хотя бы один раз в жизни. За сходство с оригиналом не ручаюсь, художник из меня тот ещё, но тем не менее.
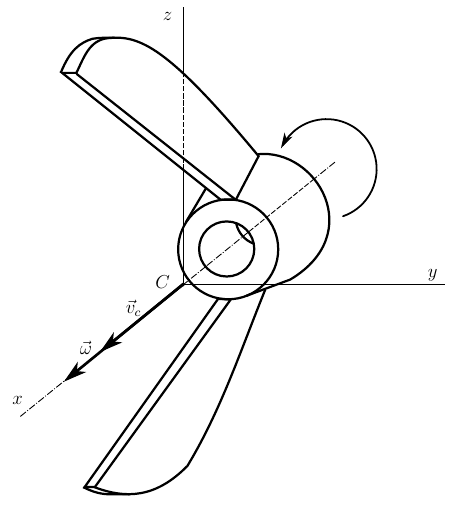
Во-первых, движение гайки (пока что, хотя моделирование в планах есть) мы будем изучать качественно. Поэтому нас не будут интересовать конкретные размеры этого изделия. Нам важна форма этой гайки, из которой мы, практически ничего не вычисляя можем сделать некоторые выводы.
Гайка совершает свободное движение, поэтому в качестве полюса удобно выбрать её центр масс. Кроме того, пусть собственная система координат (связанная с телом) будет декартовой, а её оси пусть совпадают с главными осями инерции. Такие оси всегда можно найти, и они будут ортогональны, что мы строго доказывали в предыдущей статье. Так что мы можем считать, что центральный тензор инерции гайки будет представлен диагональной матрицей
)

Очевидно, что наибольшим главным осевым моментом инерции будет — гайка имеет наиболее протяженную форму именно в плоскости, перпендикулярной оси
— гайка имеет наиболее протяженную форму именно в плоскости, перпендикулярной оси  . Насчет моментов инерции
. Насчет моментов инерции  и
и  можно поспорить — всё зависит от соотношения толщины центральной части к её диаметру и удаленности центра масс от резьбового отверстия, но допустим, что форма гайки такова, что
можно поспорить — всё зависит от соотношения толщины центральной части к её диаметру и удаленности центра масс от резьбового отверстия, но допустим, что форма гайки такова, что  . Тогда введем безразмерные моменты инерции
. Тогда введем безразмерные моменты инерции
)

и, так как
)

В этом случае центральный тензор инерции принимает вид
)

Так как после схода с резьбы гайка движется как свободное тело, форма записи уравнений движения очевидна
)
%20%3D%20%5Csum%20%5Cvec%20M_%7Bc%7D(%5Cvec%20F_k%5E%7B%5C%2Ce%7D)%20%0A%5Cend%7Balign*%7D%20%0A)
Поскольку гайка движется в неинерциальной системе отсчета, свободно падающей на Землю (кабина космического корабля, невесомость), приняв допущение о незначительности сопротивления воздуха и пренебрегая прочими возмущениями, правые части системы (5) будем считать нулевыми
)
%20%3D%200%0A%5Cend%7Balign*%7D%20%0A)
С учетом начальных условий уравнение движения полюса легко интегрируется, и мы получаем равномерное и прямолинейное движение центра масс. Вся соль во втором уравнении, которое тоже легко интегрируется, ведь его левая часть — абсолютная производная от момента количества движения гайки относительно центра масс
%20%3D%20%5Cfrac%7B%5Ctilde%20d%5Cvec%20L_c%7D%7Bdt%7D%20%2B%20%5Cvec%5Comega%20%5Ctimes%20%5Cvec%20L_c%20%3D%20%5Cfrac%7Bd%5Cvec%20L_c%7D%7Bdt%7D%0A)
где — локальная производная МКД, взятая в связанной системе координат, а сама формула носит название формулы Бура.
— локальная производная МКД, взятая в связанной системе координат, а сама формула носит название формулы Бура.
Таким образом и второе уравнение дает интеграл

который говорит о неизменности МКД. Учитывая, что в начале угловая скорость направлена строго вдоль оси , МКД так же будет направлен вдоль той же оси, ибо несимметричность тела в этом случае влияния оказывать не будет, МКД будет иметь проекцию на ось
, МКД так же будет направлен вдоль той же оси, ибо несимметричность тела в этом случае влияния оказывать не будет, МКД будет иметь проекцию на ось  и она будет равна
и она будет равна  . Откуда тогда берутся эволюции, описанные в опыте Джанибекова?
. Откуда тогда берутся эволюции, описанные в опыте Джанибекова?
Предположим, что под действием короткого малого возмущения, угловая скорость гайки отклонилась от закона, который дают уравнения (6) на малую величину . Тогда угловая скорость гайки станет равна
. Тогда угловая скорость гайки станет равна
)

Перепишем второе уравнение (6) в тензорном виде

и подставим туда (7)
)
%20%2B%20%5Cvarepsilon%5E%7B%5C%2Crkm%7D%20%5C%2C%20%5Cleft(%5Comega_%7B%5C%2Ck%7D%20%2B%20%5CDelta%20%5Comega_%7B%5C%2Ck%7D%5Cright)%20%5C%2C%20g_%7B%5C%2Cms%7D%20%5C%2C%20I_%7B%5C%2Cp%7D%5E%7B%5C%2Cs%7D%20%5C%2C%20%5Cleft(%5Comega%5E%7B%5C%2Cp%7D%20%2B%20%5CDelta%20%5Comega%5E%7B%5C%2Cp%7D%5Cright)%20%3D%200%0A)
Раскроем в (8) скобки
)

Однако, , что соответствует установившемуся режиму движения. Последнее слагаемое (9) отбрасываем как малое 2-го порядка, приводя уравнение (9) к виду
, что соответствует установившемуся режиму движения. Последнее слагаемое (9) отбрасываем как малое 2-го порядка, приводя уравнение (9) к виду

Пересчитаем компоненты угловой скорости по формулам
)

Подставим (10) в (9) и вынесем за скобку общие множители
%20%5C%2C%20%5CDelta%5Comega%5E%7B%5C%2Cl%7D%20%3D%200%0A)
Используя свойства дельты Кронекера и опуская индексы у тензора инерции, получаем
%20%5C%2C%20%5CDelta%5Comega%5E%7B%5C%2Cl%7D%20%3D%200%0A)
или
)

где) — тензор ранга
— тензор ранга ) .
.
Полученная система уравнений (11) называется линеаризованной системой уравнений возмущенного движения и служит для исследования устойчивости установившегося движения по первому приближению.
Обратите внимание, оперируя тензорами мы начисто забыли о том, что в уравнении (6) имеется страшное матричное умножение да ещё и векторное произведение. Ещё одна иллюстрация мощности тензорного подхода к преобразованию векторно-матричных форм.
Снова перейдем к матричной форме в уравнении (11), разрешив его относительно производной отклонений угловой скорости
)

Первый метод Ляпунова, который мы будем использовать для оценки устойчивости движения гайки предусматривает исследование собственных чисел матрицы . Для того, чтобы установившееся движение было устойчивым, собственные числа (которых будет три) матрицы
. Для того, чтобы установившееся движение было устойчивым, собственные числа (которых будет три) матрицы  должны иметь отрицательные действительные части.
должны иметь отрицательные действительные части.
Однако, для начала нам следует получить матрицу , элементы которой удовлетворяют тензорному соотношению
, элементы которой удовлетворяют тензорному соотношению
)
%0A)
Для начала вспомним, что мы работаем в декартовых координатах, значит метрический тензор представлен единичной матрицей, тензор Леви-Чивиты — символами Веблена, о которых мы уже говорили, а тензор инерции ранга) совпадает с тензором инерции ранга
совпадает с тензором инерции ранга ) .
.
Для свертки выражения (13) можно воспользоваться СКА, но так как я ещё не разобрался с покомпонентной работой с тензорами в Maxima и Maple, то быстро набросал следующий код в Maple, пользуясь её средствами линейной алгебры
Пропустив исходные данные через Maple, на выходе получаем матрицу
%20%5C%5C%0A0%20%26%26%20%5Comega%20%5C%2C%20I_x%20%5C%2C%20%5Cleft(i_y%20-%201%5Cright)%20%26%26%200%0A%5Cend%7Bbmatrix%7D%0A)
где — угловая скорость вращения гайки сразу после схода с резьбы на установившемся участке движения, перед кувырком. Эту угловую скорость можно считать постоянной.
— угловая скорость вращения гайки сразу после схода с резьбы на установившемся участке движения, перед кувырком. Эту угловую скорость можно считать постоянной.
Нетрудно получить и матрицу

Характеристическое уравнение для вычисления собственных чисел данной матрицы имеет вид
(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%20%5C%2C%20%5Clambda%20%3D%200%0A)
Решая его получаем собственные числа
)
(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%7D%2C%20%5Cquad%20%5C%2C%20%5Clambda_3%20%3D%20-%5Comega%20%5C%2C%20%5Csqrt%7B%5Cfrac%7B(i_y%20-%201)(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%7D%0A)
Собственные числа принимают действительные значения, если безразмерные моменты инерции удовлетворяют условию
)

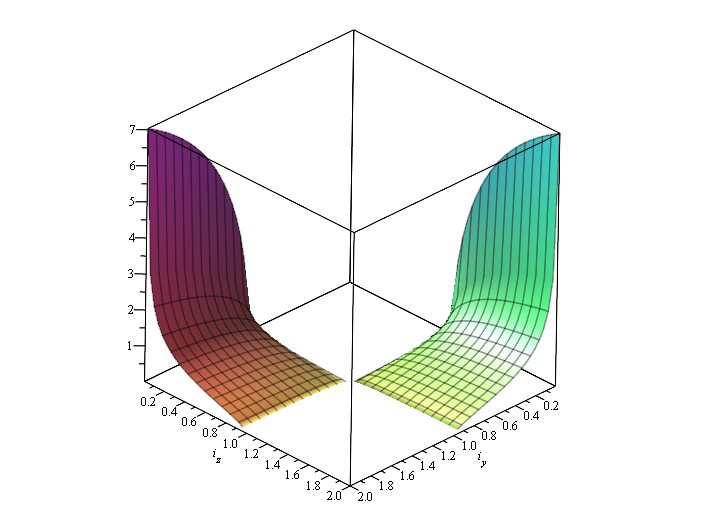
В противном случае два собственный числа будут чисто мнимыми. Если мы построим графики зависимости собственных значений и
и  от безразмерных моментов инерции, то увидим, что при нарушении условия (15) графики проваливаются в комплексную область.
от безразмерных моментов инерции, то увидим, что при нарушении условия (15) графики проваливаются в комплексную область.
Положительный корень характеристического полинома
Отрицательный корень характеристического полинома

Хотя бы одно собственное значение с положительной вещественной частью говорит о неустойчивости установившегося режима движения.
Теперь посмотрим, ведь условие (15) удовлетворяет принятому нами в начале условию (3). При соотношении между моментами инерции, когда

то есть, будучи изначально закрученной вокруг оси с промежуточным между максимальным и минимальным значением момента инерции, гайка ведет себя неустойчиво, совершает переворот, а затем снова пытается найти устойчивое положение, и снова совершает переворот. Известно, что устойчивые вращения свободного тела возможны лишь вокруг осей с максимальным и минимальным моментом инерции.
Если
)

то мы получаем чисто мнимые корни характеристического уравнения, и первый метод Ляпунова не отвечает однозначно на вопрос, будет ли устойчиво движение в этом случае. Но исходя из того, что знает механика не сегодняшний день и из колебательного характера решения линейных уравнений с мнимыми корнями характеристического уравнения, можно предположить периодические колебания вектора угловой скорости около установившегося режима, что соответствует процессам прецессии и нутации.
В этой связи, наша планета, удовлетворяющая условию (16) не будет испытывать на себе эффект Джанибекова. Так что глобальная катастрофа со сменой полюсов нам не грозит.
Данная статья была некоторой разминкой. К гайке «барашку» мы, возможно ещё вернемся, а пока — благодарю моих читателей за внимание!
>Продолжение следует…
Введение
Данное видео иллюстрирует повторный эксперимент — вместо «барашка» используется какая-то самодельная ерунда
Это случилось в 1985 году, на орбитальной станции «Салют-7», во время посещения её экипажем корабля «Союз Т-13» в составе космонавтов Джанибекова В. А. и Савиных В. П. Не буду описывать своими словами, процитировав один из многочисленных сетевых источников
Когда космонавты распаковывали доставленный на орбиту груз, то им приходилось откручивать так называемые «барашки» – гайки с ушками. Стоит ударить по ушку «барашка», и он сам раскручивается. Затем, раскрутившись до конца и соскочив с резьбового стержня, гайка продолжает, вращаясь, лететь по инерции в невесомости (примерно как летящий вращающийся пропеллер). Так вот, Владимир Александрович заметил, что пролетев примерно 40 сантиметров ушками вперед, гайка вдруг совершает внезапный переворот на 180 градусов и продолжает лететь в том же направлении, но уже ушками назад и вращаясь в другую сторону. Затем, опять пролетев сантиметров 40, гайка снова делает кувырок на 180 градусов и продолжает лететь снова ушками вперед, как в первый раз и так далее. Джанибеков неоднократно повторял эксперимент, и результат неизменно повторялся. В общем, вращающаяся гайка, летящая в невесомости, совершает резкие 180-градусные периодические перевороты каждые 43 сантиметра. Также он пробовал вместо гайки использовать другие предметы, например, пластилиновый шарик с прилепленной к нему обычной гайкой, который точно так же, пролетев некоторое расстояние, совершал такие же внезапные перевороты.
Думаю, что для затравки этого вполне достаточно. На самом деле, в «эффекте Джанибекова» нет ничего экстраординарного (хотя ему причисляют и возможную смену полюсов Земли каждые 12000 лет, и прочие глобальные катаклизмы). Используя аппарат тензорной алгебры и теорию устойчивости механического движения, попробуем разобраться, что происходит с загадочной гайкой.
1. Гайка «барашек» — массово-инерционные характеристики
На рисунке изображен объект нашего исследования. Наверняка каждый из читателей видел такую гайку хотя бы один раз в жизни. За сходство с оригиналом не ручаюсь, художник из меня тот ещё, но тем не менее.

Во-первых, движение гайки (пока что, хотя моделирование в планах есть) мы будем изучать качественно. Поэтому нас не будут интересовать конкретные размеры этого изделия. Нам важна форма этой гайки, из которой мы, практически ничего не вычисляя можем сделать некоторые выводы.
Гайка совершает свободное движение, поэтому в качестве полюса удобно выбрать её центр масс. Кроме того, пусть собственная система координат (связанная с телом) будет декартовой, а её оси пусть совпадают с главными осями инерции. Такие оси всегда можно найти, и они будут ортогональны, что мы строго доказывали в предыдущей статье. Так что мы можем считать, что центральный тензор инерции гайки будет представлен диагональной матрицей
Очевидно, что наибольшим главным осевым моментом инерции будет
и, так как
В этом случае центральный тензор инерции принимает вид
2. Дифференциальные уравнения установившегося движения гайки
Так как после схода с резьбы гайка движется как свободное тело, форма записи уравнений движения очевидна
Поскольку гайка движется в неинерциальной системе отсчета, свободно падающей на Землю (кабина космического корабля, невесомость), приняв допущение о незначительности сопротивления воздуха и пренебрегая прочими возмущениями, правые части системы (5) будем считать нулевыми
С учетом начальных условий уравнение движения полюса легко интегрируется, и мы получаем равномерное и прямолинейное движение центра масс. Вся соль во втором уравнении, которое тоже легко интегрируется, ведь его левая часть — абсолютная производная от момента количества движения гайки относительно центра масс
где
Таким образом и второе уравнение дает интеграл
который говорит о неизменности МКД. Учитывая, что в начале угловая скорость направлена строго вдоль оси
3. Дифференциальные уравнения возмущенного движения гайки
Предположим, что под действием короткого малого возмущения, угловая скорость гайки отклонилась от закона, который дают уравнения (6) на малую величину
Перепишем второе уравнение (6) в тензорном виде
и подставим туда (7)
Раскроем в (8) скобки
Однако,
Пересчитаем компоненты угловой скорости по формулам
Подставим (10) в (9) и вынесем за скобку общие множители
Используя свойства дельты Кронекера и опуская индексы у тензора инерции, получаем
или
где
Полученная система уравнений (11) называется линеаризованной системой уравнений возмущенного движения и служит для исследования устойчивости установившегося движения по первому приближению.
Обратите внимание, оперируя тензорами мы начисто забыли о том, что в уравнении (6) имеется страшное матричное умножение да ещё и векторное произведение. Ещё одна иллюстрация мощности тензорного подхода к преобразованию векторно-матричных форм.
4. Исследование устойчивости движения гайки Джанибекова по первому приближению (первый метод Ляпунова)
Снова перейдем к матричной форме в уравнении (11), разрешив его относительно производной отклонений угловой скорости
Первый метод Ляпунова, который мы будем использовать для оценки устойчивости движения гайки предусматривает исследование собственных чисел матрицы
Однако, для начала нам следует получить матрицу
Для начала вспомним, что мы работаем в декартовых координатах, значит метрический тензор представлен единичной матрицей, тензор Леви-Чивиты — символами Веблена, о которых мы уже говорили, а тензор инерции ранга
Для свертки выражения (13) можно воспользоваться СКА, но так как я ещё не разобрался с покомпонентной работой с тензорами в Maxima и Maple, то быстро набросал следующий код в Maple, пользуясь её средствами линейной алгебры
restart;
with(LinearAlgebra):
# Вычисление тензора Леви-Чивиты
levi_civita := proc(i, j, k)
local E := IdentityMatrix(3,3);
local A := Matrix(3, 3);
local i1 := 0;
A[1] := E[i];
A[2] := E[j];
A[3] := E[k];
return Determinant(Transpose(A));
end proc:
# Задаем используемые тензоры
J := Matrix( [ [I[xx], 0, 0], [0, a*I[xx], 0], [0, 0, b*I[xx]] ]);
g := IdentityMatrix(3, 3);
Omega := Vector([omega, 0, 0]);
L := J . Omega;
# Вычисляем матрицу G
G := Matrix(3, 3);
for r from 1 to 3 do
for l from 1 to 3 do
G[r, l] := 0;
for k from 1 to 3 do
summ := 0;
for m from 1 to 3 do
summ := summ + levi_civita(r, k, m)*Omega[k]*J[m, l] + levi_civita(r,k,m)*g[k,l]*L[m];
end do:
G[r, l] := G[r, l] + summ;
end do:
end do:
end do:
Пропустив исходные данные через Maple, на выходе получаем матрицу
где
Нетрудно получить и матрицу
Характеристическое уравнение для вычисления собственных чисел данной матрицы имеет вид
Решая его получаем собственные числа
Собственные числа принимают действительные значения, если безразмерные моменты инерции удовлетворяют условию
В противном случае два собственный числа будут чисто мнимыми. Если мы построим графики зависимости собственных значений
Положительный корень характеристического полинома

Отрицательный корень характеристического полинома
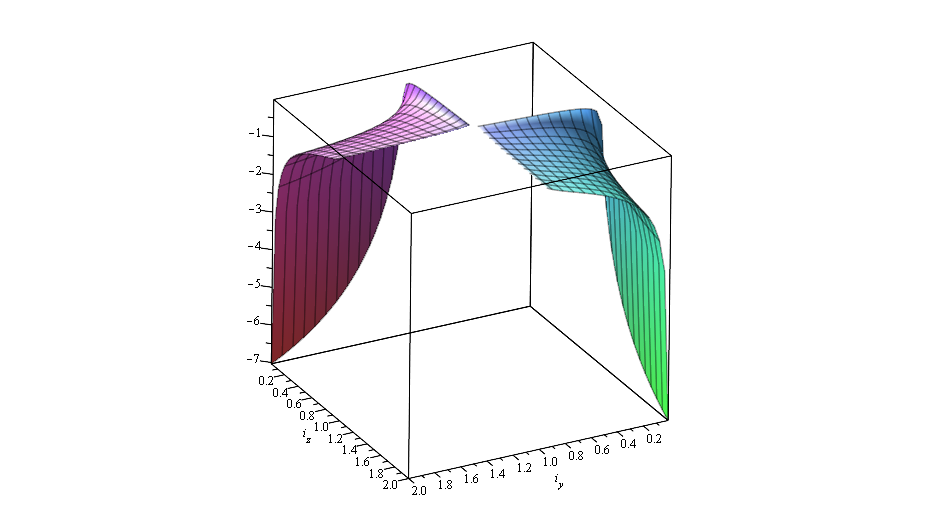
Выводы
Хотя бы одно собственное значение с положительной вещественной частью говорит о неустойчивости установившегося режима движения.
Теперь посмотрим, ведь условие (15) удовлетворяет принятому нами в начале условию (3). При соотношении между моментами инерции, когда
то есть, будучи изначально закрученной вокруг оси с промежуточным между максимальным и минимальным значением момента инерции, гайка ведет себя неустойчиво, совершает переворот, а затем снова пытается найти устойчивое положение, и снова совершает переворот. Известно, что устойчивые вращения свободного тела возможны лишь вокруг осей с максимальным и минимальным моментом инерции.
Если
то мы получаем чисто мнимые корни характеристического уравнения, и первый метод Ляпунова не отвечает однозначно на вопрос, будет ли устойчиво движение в этом случае. Но исходя из того, что знает механика не сегодняшний день и из колебательного характера решения линейных уравнений с мнимыми корнями характеристического уравнения, можно предположить периодические колебания вектора угловой скорости около установившегося режима, что соответствует процессам прецессии и нутации.
В этой связи, наша планета, удовлетворяющая условию (16) не будет испытывать на себе эффект Джанибекова. Так что глобальная катастрофа со сменой полюсов нам не грозит.
Данная статья была некоторой разминкой. К гайке «барашку» мы, возможно ещё вернемся, а пока — благодарю моих читателей за внимание!
>Продолжение следует…