Comments 60
Причем доказать, что существует требуемая прямая, параллельная произвольно выбранной довольно примитивно через параллельный сдвиг прямой и функцию разности площадей справа и слева как сумму нескольких непрерывных функций, принимающую значения А и -А с разных сторон от прямоугольника, а следовательно принимающую и значение 0 хотя бы в одной позиции.
Интересно, что это было за интервью.
Почему у меня глаз сразу зацепился за «подковерное» изменение задачи — в современном программостроении очень трудно найти проект сложнее Hello World в котором это не сыграло бы ощутимую роль. Чаще всего — негативную.
Возьмем произвольную прямую. Пересечение одной полуплоскости, ограничеваемой этоий прямой, с прямоугольником с дыркой назовем фигурой А, другой полуплоскости фигурой Б. Будем двигать эту прямую вдоль нормали к ней, и рассмотрим разность площадей А и Б. очевидно что она меняет знак, а значит есть точка где разность равна нулю.
Чуть-чуть не успел.
Сейчас вообще в школе проходят задачи с циркулем и линейкой?
если круг очень маленький, а прямоугольник большой, то IMHO вообще неважно где круг.
Навык? Наличие навыка показывает умение решать шаблонные задачи. Тут, скорее, я бы заподозрил попытку проверить умеет ли человек решать как раз нетиповые задачи (исходя из предположения, что большинство соискателей вышли из школьно-студенческого возраста и олимпиадные навыки успешно утратили со временем). Но, боюсь, это слишком сложная конспирология и большинство просто решило, — а почему бы и нет. И, как ни странно, оно даже так работает :). Полезно, если у вас в работе, конечно, встречаются нетиповые задачи. Если не встречаются и нужно тупое производство шаблонного кода с незначительными вариациями, то да, это всё лишнее, а подобный работник будет overqualified, быстро заскучает и уйдёт.
Решение подобной задачи покажет, может ли человек разбираться с незнакомыми поставленными задачами.
Всего две задачки, но насколько интересные…
Спасибо, что дали повод немножко подумать :)
Задача 1.
Легко увидеть, что через любую точку на периметре прямоугольника (при условии что вычитаемый круг находится полностью внутри прямоугольника, не касаясь его сторон) можно провести только одну прямую, которая разделит фигуру пополам.
Кстати, если для каждой точки периметра P провести прямую, делящую фигуру пополам, найти вторую точку её пересечения с периметром прямоугольника, и найти точку Q середины отрезка прямой между данными двумя точками… то если точка P пробегает множество всех точек периметра прямоугольника, должна получиться замкнутая фигура из множества точек Q… Интересно, как выглядит данная фигура? :)
Впрочем, мне кажется, надо меньше расстояния по периметру пробегать, но это будет не половина периметра — надо провести через начальную точку P0 прямую, делящую фигуру пополам, определить вторую точку пересечения данной прямой с периметром P1, а затем пробегать по периметру от P0 до P1 в любом направлении :)
В любом случае ответ я бы дал так: бесконечное количество прямых, соизмеримое с [бесконечным] количеством точек на периметре прямоугольника...
Задача 2.
Из того, что 4 точки не лежат на одной плоскости, сразу следует вывод: эти точки образуют объёмную фигуру с ненулевым объёмом, т.е. тетраэдр.
Соответственно, следует искать множество точек, которые будут равноудалены от всех вершин данного тетраэдра.
Надо полагать, что все плоскости, удовлетворяющие условиям задачи, должны пересекаться с этим тетраэдром, и ни одна точка снаружи тетраэдра не будет равноудалена от всех его вершин.
Как именно пересекаться? Совершенно очевидно, что любое ребро тетраэдра, пересекаемое искомой плоскостью, будет делиться ею ровно пополам, иначе нарушится условие равноудалённости.
Пожалуй, надо провести высоту из вершины к противоположной грани, и через середину этой высоты провести плоскость, параллельную той грани, к которой проводили высоту.
Значит, ответ (предварительный) будет таков: 4 (по количеству вершин тетраэдра)
На этом мои самостоятельные мысли по задаче 2 закончились, и я воспользуюсь тем, в тексте указано наличие 2-х разных случаев (4+3) и окончательный ответ 7 :)
Мои мысли дали только 1-й случай, когда по одну сторону плоскости лежит одна точка, а по другую — три. Значит, я упустил случай, когда две точки по одну сторону искомой плоскости и две по другую.
Что ж, давайте подумаем, как проводить плоскость через тетраэдр по 2-му случаю… Бррр, как тяжело на нетрезвую голову представить такие варианты, но я таки справился :) Всё отличие в том, что вместо 3-х рёбер искомая плоскость будет пересекать 4 ребра. А каково количество различных сочетаний по 4 ребра из 6? Ага, 6!/(4!(6-4)!) = 56/2! = 30/2 = 15… Э-э-э, ошибка, 15 — это много… Загуглим слово "тетраэдр" и посмотрим картинки… А-а-а, ведь надо брать не любые 4 ребра, а только такие, чтобы оставшиеся 2 ребра не имели общих точек… А сколькими способами можно взять 2 ребра, чтобы они не имели общих точек? Ну да, если точки пронумеровать: 0,1,2,3, то "вручную" считаем комбинации — (0+1; 2+3), (0+2; 1+3), (0+3; 1+2), и всё! Ровно три "недостающих" комбинации и получили :)) Ура!!!
Ответ: 4 + 3 = 7 штук!
1)Находим центры прямоугольника и круга.
2)Соединяем центры отрезком. На этом отрезке находится центр тяжести получившейся фигуры. (его просто вычислить, но одного циркуля с линейкой скорее всего не хватит)
Через этот центр можно провести бесконечное количество секущих.
Однако в большинстве случаев существуют точки на… прямоугольника, через которые можно провести бесконечное количество равновеликих секущих.
При определении центра масс нужно оперировать такими понятиями как радиус-вектор/момент силы тяжести/плечо. Можно уравновесить абсолютно разные массы, если подобрать плечи разной длины.
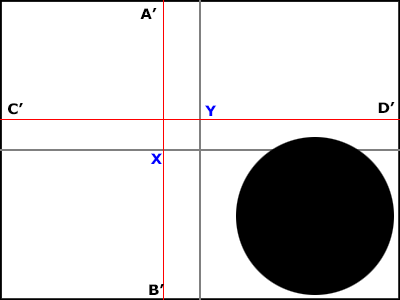
Сделал на скорую руку иллюстрацию. Средние линии обозначены серым цветом. Равновеликие — красным. При перемещении круга внутри красного правого нижнего прямоугольника центр масс будет смещаться (так как будут меняться радиус-векторы), а равновеликие секущие — нет (так как площадь правого нижнего красного прямоугольника останется постоянной).
Нетрудно заметить, что если точки X и Y не принадлежат кругу, то через каждую из них можно провести бесконечное количество равновеликих секущих. (но не равновесных!)
Из 4 точек не лежащих в одной плоскости можно выбрать 3 не лежащих на одной прямой и посторить по ним плоскость из варианта 1.
Или я что-то упускаю?
2) по каждую сторону от плоскости лежат по две точки.
Я не могу представить, как можно спутать эти варианты или преобразовать один в другой. В этих вариантах совершенно разные построения.
Мы искомую плоскость проводим, ее нет. Изначально у нас есть только 4 точки и все.
Поэтому я предположил такой алгоритм:
— берем 3 любые точки (они не могут лежать на 1 прямой, иначе все 4 точки окажутся в одной плоскости)
— строим по этим 3 точкам плоскость
— строим от 4 точки перпендикуляр до этой плоскости
— искомая плоскость — по центру перпендикуляра (параллельно 3-х точковой)
— повторяем с другим набором из 3 точек (итого: сколько не повторяющихся наборов из 3 точек из всего множества 4 точек — столько и плоскостей)
Существует движение пространства, при котором координаты точек будут иметь вид (иначе все точки лежат в одной плоскости):
K(0, 0, 0), M(x[m], 0, 0), L(x[l], y[l], 0), N(x[n], y[n], z[n]), причем x[m] * y[l] * z[n] != 0 (иначе все точки лежат в одной плоскости)
Пусть уравнение искомой плоскости П в данной системе координат имеет вид:
A * x + B * y + C * z + D = 0, D >= 0 (это всегда можно сделать так)
Пусть n = Sqrt[A^2 + B^2 + C^2]
dist(П, K) = D / n
dist(П, M) = Abs[A * x[m] + D] / n
dist(П, L) = Abs[A * x[l] + B * y[l] + D] / n
dist(П, L) = Abs[A * x[n] + B * y[n] + C * z[n] + D] / n
Тогда имеем систему уравнений:
{Abs[A * x[m] + D] == D, Abs[A * x[l] + B * y[l] + D] == D, Abs[A * x[n] + B * y[n] + C * z[n] + D] == D}
Всевозможными способами раскрывая модуль, получаем решения системы (8 семейств).
Одно из них не подходит, т. к имеет вид A = B = C = 0
Каждое другое задает соответствующую плоскость. Значит, существует всего 7 искомых плоскостей.
Как ни крути, а знания лишними не бывают
Знания лишними не бывают. Но ты решаешь эти задачи на собеседовании (легко и слету), а на работу тебя все равно не берут. Потому что Google.
Как ни крути, а знания лишними не бывают
Даже если предположить, что возможности мозга не ограничены, и человек (без потери, а вроде как с пользой) способен впитать в себя огромное количество знаний — то остается, как минимум, еще один фактор: время. Оно крайне лимитировано. Поэтому знания, как и всё остальное, стоит выбирать с точки зрения целесообразности.
Нужна ли программисту математика? Вечный холиварный вопрос. Хочу отметить, на один из комментариев выше, что в реальной жизни проекты не делятся на «тупой кодинг» и наукоемкие, с кучей математики. 99% задач где-то между ними. Программисту в первую очередь нужна computer science, которая частично пересекается с математикой (построена на ней), но большинство задач реального мира далеки от олимпиадных задач.
На собеседованиях любят давать олимпиадные задачи. Сложилась такая практика. Но, честно говоря, непонятно, что положено в основу. Это какое-то очень общее представление о том, что у человека, который хорошо решает задачи на логику, комбинаторику, геометрию, условно говоря, хорошо работает мозг. Так смотреть на работу мозга — это как всех, от web-дизайнера до DBA называть «компьютерщик». Понятно, что когда человек его не напрягает, то когнитивные способности в целом падают. Мозг надо нагружать. Но чем? Если я прорешаю 100 подобных задачек, мне это поможет в написании сложной программы? Если очень обще — то да, тут мозг задействован, там задействован, тут логика, там логика и пр. Но фактически, с КПД близким к единице, мне это поможет лишь для решения 101-й задачи такого же типа. Это примерно как с IQ, высокий — о, да он гений! А по факту, этот коэффициент показывает умение проходить тесты. Это не значит, что человек сможет изобрести что-то полезное, слишком разная для мозга эта задача. В общем, не хочу никого обидеть, просто я не вижу оснований (проведенные исследования) для сложившегося многолетнего хайпа по поводу олимпиадных задачах. Кому-то оно интересно само по себе, людям нравится решать задачки — отлично! Какая-то часть мозга очень развивается. Но почему это рассматривается как обязательная часть реального программирования?
Решение первой задачи приведено для условия "прямая, которая делит на равновеликие части как оставшуюся часть прямоугольника, так и вырезанный круг".
Две геометрические задачки, которые попадались на собеседовании, и где они обитают