Comments 47
для доски любого размера можно всегда расставить ферзей один за одним лесенкойСпорное утверждение. Хотел бы увидеть для нечётного N. Например, для 9.
Давайте сначала разберемся с тем, что кажется спорным:
- Что для любого N >=4 есть решение? Подсчет числа решений вот в этой части даёт больше нуля всюду (N >= 4)
- Что их можно один за одним расставить? Ну так обе ссылки в этой части описывают это в деталях
- То, что "лесенкой"? В оригинале используется научный жаргон в духе "explicit solutions exhibit stair-stepped patterns" — который перевел "лесенкой" (если прям педантично переводить, то там должно быть "явные решения показывают закономерность сходную со ступеньками") и нужный пример вам пример даже есть по ссылке:
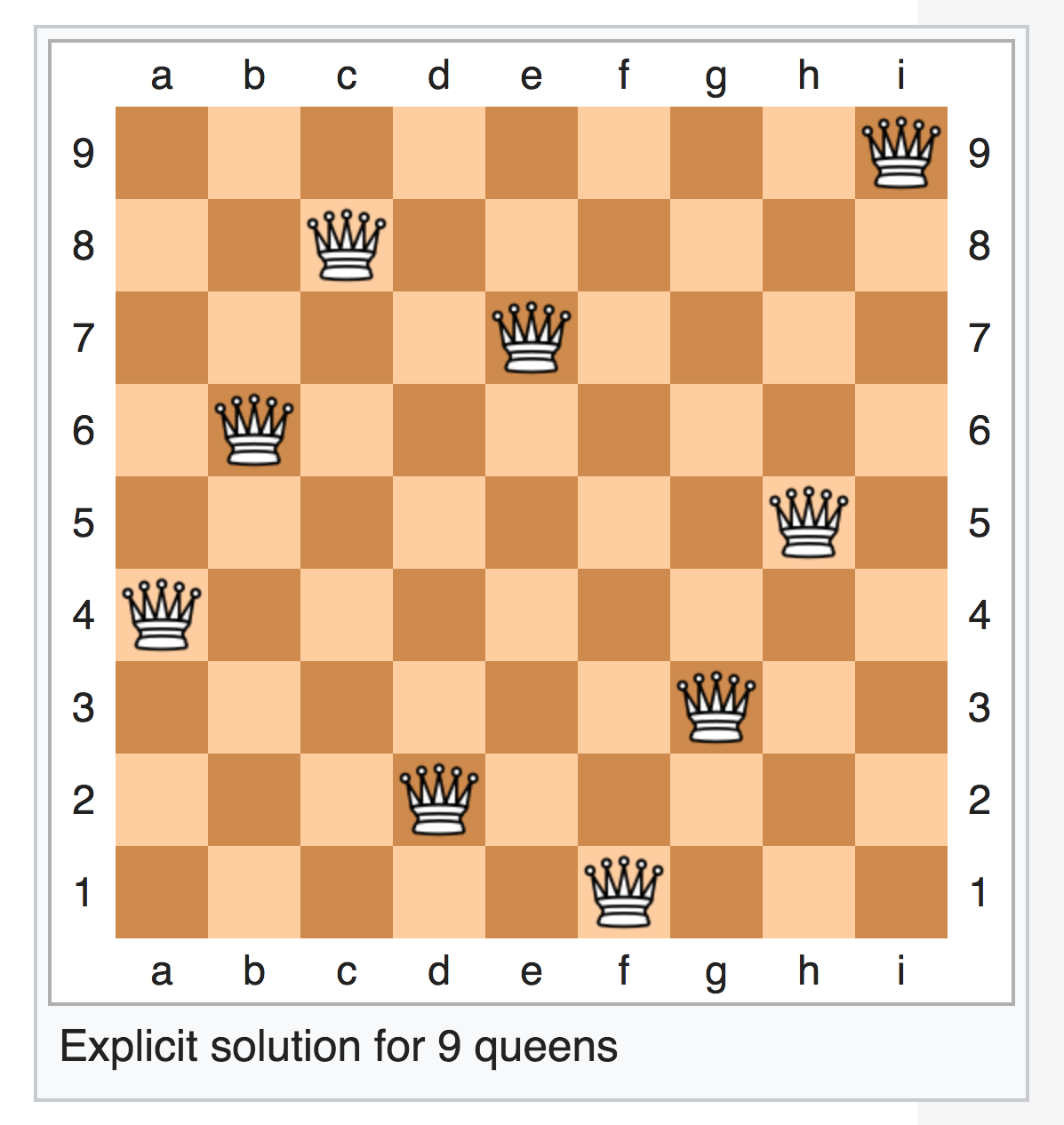
Да, определённые паттерны есть, причём для N разной кратности можно найти свои паттерны. Но это не лесенка. Это больше напомнит Г — ход шахматного коня, потому что это самые ближайшие друг к другу клетки, с которых ферзи не бьют друг друга.
Они не стоят "один за одним" — она ставятся один за одним (ставим первого, потом второго, третьего и никогда не меняем предыдущих позиций) — в этом разница с дополнением, там их нельзя поставить один за одним — их нужно ставить все сразу.
"Лесенка" тут взялась из того, что шаг алгоритма делает что-то похожее на ступеньку (иногда выскакивая за доску и делая mod оказывается на другой стороне) — хотите можете дать этому другое название — здесь это нужно исключительно в качестве иллюстрации, если не помогает, а буква Г помогает, то почему бы и нет.
Отлично, надо бы организовать Хабра-цикл статей по ASP :-)
Не вопрос — мне тут еще диссертацию надо доредактировать, так что к январю — это еще хорошо :-)
Ого, эту сужает список возможных университетов где-то до 10 (на самом деле нет) :) Потсдам?
Если это опубликовать, то в Потсдаме будут всегда рады — они активно ищут людей :-)
На CP Minizinc (Gecode) для N=150 находит решение за 7 сек, а с дополнениями еще быстрее.
int: n;
array [1..n] of var 1..n: q;
predicate
noattack(int: i, int: j, var int: qi, var int: qj) =
qi != qj /\
qi + i != qj + j /\
qi - i != qj - j;
constraint
forall (i in 1..n, j in i+1..n) (
noattack(i, j, q[i], q[j])
);
solve satisfy;
output [ if fix(q[i]) = j then "Q " else ". " endif ++
if j = n then "\n" else "" endif
| i, j in 1..n
];Ну технологии и правда родственные: главные CP и ASP конференции в этом году вообще вместе проводили. Где-то ASP чуть интересней, где-то CP. На мой вкус ASP как-то естественней, чем CP, особенно для реляционных задач, но тут я совсем biased :-)
Если даже для 8-ми ферзей их 92.
Короче говоря, есть несколько задач связанных между собой, которые неразрешимы на данный момент для достаточно большой доски, например, 1000x1000:
1) нахождение числа всех возможный расстановок ферзей;
2) нахождение числа возможных расстановок, когда на доске уже установлены одна или более фигур;
3) нахождение хотя бы одной правильной расстановки, когда на доске уже установлены одна или более фигур (либо указание невозможности расставить остальные фигуры).
Последняя задача интуитивно кажется наиболее простой, однако так ли это на самом деле — неизвестно. Чтобы понять сложность задачи попробуйте расставить несколько ферзей случайным образом на большой доске и затем отыскать хотя бы одно решение, в котором фигуры не бьют друг друга.
Можно высказать предположение, что для достаточно большой доски существует алгоритм, расставляющий фигуры за меньшее количество операций, чем банальный поиск перебором (при условии что на доске уже стоит хотя бы одна фигура!). Если такой алгоритм будет найден или это предположение будет доказано иным способом, можно утверждать, что P=NP.
SAT не делает "банального поиска с перебором" — но это никак не даёт нам P=NP
Можно высказать предположение, что для достаточно большой доски существует алгоритм, расставляющий фигуры за меньшее количество операций, чем банальный поиск перебором (при условии что на доске уже стоит хотя бы одна фигура!). Если такой алгоритм будет найден или это предположение будет доказано иным способом, можно утверждать, что P=NP.
можно утверждать = будет доказано?
А можно весьма наивный вопрос?
есть несколько задач связанных между собой, которые неразрешимы на данный момент для достаточно большой доски, например, 1000x1000:
[...]
3) нахождение хотя бы одной правильной расстановки, когда на доске уже установлены одна или более фигур
Если рассмотреть вырожденный случай, когда у нас уже есть готовое корректное решение для доски 999х999, правильно ли я понимаю, что задача дополнения до доски в 1000 тривиальна: надо просто проверить диагональ в доске 999? И аналогичное верно для любого перехода от расставленной доски n-1 к доске n?
Я никоим образом не говорю, что из этого вырожденного случая можно сделать какие-то обобщения для всех расстановок, просто хочу проверить свое наивное понимание задачи.
Ну и в качестве второго вопроса: вот тут человек, вроде как, пишет, что разработал алгоритм дополнения за линейное (!) время. Пора хоронить P vs NP, или я неправильно что-то прочитал?
Представим, что дана доска 1000х1000 с 500 королев и в ней пропущены 500 не с края, а хаотично здесь одна, там вторая и тд. Не получится дополнить — потому что расстановка дальше может быть фиксирована условиями, а не вашим алгоритмом.
Я уже отвечал этому человеку в личной переписке, кажется, он не очень понимает некоторых вещей, если честно. Есть алгоритм для P = NP за линейное время? Мы хотим результатов на стандартных SAT benchmarks с корректными результатами и линейным временем исполнения. Доказательств нет, но есть громкие заявления.
Если вся доска 999х999 заполнена корректно, то дополнить в принципе несложно (надо перебрать все оставшиеся клетки, например) — только задача не в этом.
Я понимаю, что задача не в этом. Я просто не так давно начал смотреть на n-queens, и хотел проверить свою интуицию для конкретного очень простого случая — просто потому, что если я и в таком простом случае ошибаюсь, то рассуждать дальше мне не стоит.
Спасибо за ответ.
"Если, говорить упрощенно" — я завис на этой запятой
(белые не бьют белых, а черные черных)
Судя по иллюстрации, всё как раз наоборот?
у ASP тоже загадочная русская душа: он временами запутан и непредсказуем для непосвященных; кстати, теория, лежащая в основе современного ASP, была придумана в 1988ом году Михаилом Гельфондом и Владимиром Лифшицем
О да, фамилии выдают в них истинных носителей загадочной русской души
(белые не бьют белых, а черные черных)
Судя по иллюстрации, всё как раз наоборот?
Если белые бьют белых, то как они стоят на одной строке? см. например самую верхнюю
О да, фамилии выдают в них истинных носителей загадочной русской души
Пушкину, она судя по этой логике, тоже не полагается?
(белые не бьют белых, а черные черных)
Судя по иллюстрации, всё как раз наоборот?
Если белые бьют белых, то как они стоят на одной строке? см. например самую верхнюю
Наоборот — это «белые не бьют чёрных, а чёрные белых».
Тут видимо у нас какая-то путаница в определениях: "белые не бьют белых" = белые не атакуют белых в принципе, т.е., это ок для решения, если белый ферзь стоит на одной диагонали, строке или столбце с другим белым ферзём — но это НЕ ок, если белый стоит на одной диагонали/строке/колонке с черным.
Видимо ваша интерпретация примерно такая, решение — это два множества пар W = { (x,y) } и B = { (x,y) }, таких ни один ферзь (x_w,y_w) из W "не бьёт" (= стоит на одной...) ни одного ферзя (x_b, y_b) из B.
Так? Если да, то это вопрос того, что означает фраза естественного языка: "белые не бьют белых" итд.
Что касается загадочной русской души Пушкина: нам неизвестно, считал ли он себя русским, или его провозгласили русским «задним числом». Есть даже анекдот про это.
Посмотрите статью, например. Там формулировка исходной задачи именно такая: "расставить на шахматной доске 8 ферзей так, чтобы ни один из них не бил другого".
Кстати, и по вами приведённой ссылке: we are required to place two equal-sized armies of black and white queens on a chessboard so that the white queens do not attack the black queens (and necessarily vice versa) and to find the maximum size of two such armies.
А вы используете эти слова по-разному. Для вас «не бьёт», кажется, означает «не может срубить». То есть пусть себе атакует, последствий не будет всё равно.
И это несколько сбивает, да.
На счёт задачки о 19 ферзях.
Смог написать программу которая рассчитывает с большой скоростью.
https://wasm.in/threads/zadacha-o-19-ferzjax.24611/
На райзен 3600х один вариант 4.3-4.5 тактов, это очень быстро.
Для доски 8х8 9 черных, 10 белах фр. есть 3 вариант, их давно нашли вручную.
> была придумана в 1988ом году Михаилом Гельфондом...
Гельфандом.
Интересно, что латинские квадраты получили применение в таких областях, как селекция растений.
У Мартина Гарднера есть такая игра типа нима, которую он придумал: на каждом ходе игроки выставляют на шахм. доску ферзя так, чтобы он не угрожал остальным ферзям. Кто не может сделать ход, проигрывает.
Я придумал более интересный вариант: выставить каждый раз можно как ферзя, так и коня.

Разбираемся, что же там нового открыли в задаче о ферзях