Comments 61
Я уже показал, что проще ничего быть не может, но вскоре установил, что этой единственной небольшой аксиомы было достаточно, чтобы создать всю логику…
Откуда мне было знать, что она верна? Потому что я заставил компьютер доказать её.
Аксио́ма (др.-греч. ἀξίωμα «утверждение, положение») или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами.
Сложно читать статью, которая imho начинается с бреда. Или это трудности перевода?
И «символьная логика» немного режет слух
Аксиому можно доказать в рамках другой системы аксиом (и если две системы аксиом доказываются в рамках друг друга — то они называются эквивалентными).
Но процитированный вами фрагмент все равно звучит странно.
Приведите пример двух систем, доказывающих аксиомы друг друга.
Аксиому можно доказать в рамках другой системы аксиом
Но в терминах другой системы аксиом — она не является аксиомой.
Если я правильно понял, то он доказал, что из его аксиомы можно вывести те (напрмер, три) соотношения, которые обычно исользовались в качестве аксиом при построении логики. То есть нам для построения логики достаточно принять три аксиомы: А, Б, В. Стивен говорит, что он нашел какую-то одну аксиому Г, из которой А, Б и В получаются как следствия. Тогда одной этой аксиомы Г достаточно для построения логики. Как-то так.
Понимать надо так.
1) Для построения любой теории в математике надо выбрать систему аксиом — т.е. неких начальных утверждений, из который выводятся все остальные.
2) Булева логика давно известна, в качестве системы аксиом можно выбирать разные наборы утверждений, например аксиомы Мередита (приведены в статье чуть ниже).
3) Мы хотим, чтобы аксиомы были как можно более простыми (автор считает, что просто = мало).
4) Все известные системы аксиом содержат хотя бы два основных утверждения.
5) Автор предлагает в качестве единственной аксиомы РОВНО ОДНО утверждение.
6) Чтобы доказать, что полученная теория совпадает с Булевой логикой надо сделать две вещи:
— доказать, что аксиома автора следует из известной системы аксиом
— доказать, что любая из известных систем аксиом следует из единственной аксиомы автора.
В статье говорится примерно то же самое, только длиннее и более «по-философски».
«Функциональная полнота» NAND могла навеки остаться диковиной, если бы не разработка полупроводниковой технологии – она реализует все миллиарды логических операций в современном микропроцессоре при помощи комбинации транзисторов, выполняющих лишь функцию NAND или связанную с ней NOR.
Но это же не так!
Или вы что-то другое имели ввиду?
Насколько я знаю, довольно часто используются комбинации транзисторов, которые нельзя разбить на обособленные NAND- или NOR- блоки. Еще когда микросхемы были большими, были, например, микросхемы И-ИЛИ-НЕ. Вот ни за что не поверю, что искусство изготовления подобных схем навсегда утрачено...
А константа как раз не нужна (но только в теории!). x nand (x nand x) дает true, true nand true дает false.
>>> def nand(a, b):
return not(a and b)
>>> from spaces import print_logic_table # если кому надо, выложу на GitHub
>>> print_logic_table(
lambda p, q, r: nand(nand(nand(p, q), r), nand(p, nand(p, nand(p, r)))))
x1 x2 x3 F
------------
* * 0 0
* * 1 1
Да, действительно результат строго равен третьему параметру, то есть r.
Кстати, не понимаю, почему формулу не сократить до ((p*q)*r)*(p*r)=r. Если результат тот же, то зачем платить больше? (хотя допускаю, что именно для использования в качестве аксиомы эти два NANDа как раз и нужны)
>>> print_logic_table(
lambda p, q, r: nand(nand(nand(p, q), r), nand(p, r)))
x1 x2 x3 F
------------
* * 0 0
* * 1 1
На мой взгляд, какой-то очень объемный текст. Внимательно читать такое во время кофебрейка нереально, а к вечеру я про него уже забуду. Прощай, еще один TLDR.
Где-то во второй половине 20-го века различия между двумя этими вещами были проигнорированы, и аристотелева логика сейчас, по сути, является забытым искусством. На мой взгляд, очень зря. Например, значительная доля того, что рыхло и многословно феноменологически описывается в теме «когнитивные искажения», сводится к логическим (в смысле аристотелевой логики) ошибкам «отрицание антецедента» и «подтверждение консеквента».
В технике (а конкретно вычислительной) булева алгебра — основа основ. Аристотелева для этого не годится. У неё другое назначение — быть полезной в жизни. И в науке, кстати, тоже, поскольку научный метод строится не на булевой алгебре, а именно на базе старой доброй аристотелевой логики. Очень жалко, что эту штуку повсеместно исключили из преподавания.
Хотя в аристотелевой логике довольно много внимания уделяется конструкции «если-то», которая в булевой алгебре называется импликацией, и которую через обсуждаемый здесь NAND можно выразить вот так:
(a → b) = NAND(a, NAND(b, b))
Собственно в булевой алгебре импликация на десятых ролях. В языках программирования для неё даже оператора нет. А в жизни это ни что иное, как констатация потенциальной управляемости того предмета, которым мы желали бы управлять. Можно сказать, основа нашей практической деятельности. Не хрен собачий, правда?
У нас есть три утверждения.
А — «Все люди смертны»;
В — «Сократ человек»;
С — «Сократ смертен».
Они находятся в отношении
(A AND B) IMP C
В языках программирования для неё даже оператора нет.
А в BASIC?
Собственно в булевой алгебре импликация на десятых ролях.
Булева алгебра не сводится к языкам программирования. В любом учебнике по оной импликация чуть не через строчку встречается.
Кстати говоря, «если-то» в русском языке не соответствует поведению импликации. Точнее будет: A IPM B == А достаточно, но не необходимо для B.
(A AND B) IMP CЭто схема любого силлогизма. В том числе и такого (неправильного):
А — некоторые кони умеют играть в шахматы
В — некоторые шахматисты пьют керосин
С — некоторые кони пьют керосин
Это тоже можно записать как "(A AND B) IMP C", ну и что с того? Силлогизм всё равно не верный. Фишка в том, что в силлогистике важно, что собой внутри представляют А, В и С. Конкретно здесь мы сразу видим, что у нас две частноутвердительные посылки, и этого нам достаточно, чтобы отправить силлогизм на помойку. А для булевой алгебры А, В и С — просто двоичные переменные.
Булева алгебра бесполезна в деле разоблачения инсинуатора, затеявшего пропагандистскую кампанию в СМИ против коней.
К тому же нас должно насторожить то, что вообще-то в любом силлогизме А и В — не переменные, которые могут быть true или false, а константы, про которые известно, что они true. (true AND true) IMP C = С. И чо?
А достаточно, но не необходимо для BИ чем оно отличается от «если А, то В»? Можете привести пример с «если-то», который бы не был импликацией?
Можете привести пример с «если-то», который бы не был импликацией?
Если у меня есть картина, то я повешу картину на стену.
Пусть А — «у меня есть картина»; В — «я повешу картину на стену».
Положим A = false, a B = true, т.е. если у меня нет картины — я всё равно её повешу, не смотря на то, что её нет.
Тем не менее,
false IMP true = true
Достаточно, чтобы A было необходимым условием B и импликация разойдётся с привычным пониманием «если то».
Если у меня есть картина, то я повешу картину на стену.Это высказывание будет ложью только в том случае, если окажется, что у вас таки есть картина, но вы её не будете вешать. Вот тогда будет ай-ай-ай, нехорошо врать, обещание не сдержали. А если у вас нет картины, но вы повесили картину (например мою), то вы не соврали ни на каплю и чисты перед совестью и законом.
А вот с фразочкой «если у меня есть картина, то я повешу её на стену» интереснее. Ситуация А=false, B=true оказывается вообще запрещённой, потому что тогда вы вешаете на стенку несуществующий объект. Срабатывает внутренняя логическая зависимость.
Это высказывание будет ложью только в том случае, если окажется, что у вас таки есть картина, но вы её не будете вешать.
Отнюдь не так. Она ложна так же в том случае, если у меня нет картины, но я тем не менее повешу на стену картину. Я не могу повесить на стену картину, потому что у меня нет картины.
А если у вас нет картины, но вы повесили картину (например мою)
В исходном условии не указано, что картина должна быть моя. Раз картина есть — значит она есть.
А вот с фразочкой «если у меня есть картина, то я повешу её на стену» интереснее.
Да, интереснее. Потому что если у меня нет картины, то местоимение «её» ссылается не на картину (картины у меня нет). Поэтому я замечательно вешаю на стену нулевой указатель.
Я не могу повесить на стену картину, потому что у меня нет картиныЕсть тонкий нюанс, который нужно понимать и учитывать. Есть истинность/ложность входящих в импликацию аргументов, а есть истинность/ложность самой импликации.
Сама импликация — это правило, насчёт существования которого у нас есть какое-то мнение. А входящие в неё аргументы — это описание конкретной ситуации.
У нас может быть уверенность в аргументах импликации, а сама импликация может быть гипотезой, истинность которой мы проверяем. К слову, из конструктивных особенностей операции «импликация» следует попперовский критерий фальсифицируемости. Или, в другой ситуации, у нас может быть стопроцентная уверенность в самой импликации, и мы для получения консеквента занимаемся изготовлением антецедента. Или для предотвращения антецедента занимаемся уничтожением консеквента.
Ещё раз: истинность аргументов и истинность самой импликации — совсем разные вещи. И этот ключевой момент целиком вываливается за пределы булевой алгебры.
Что касается поиска примера того, как «если-то» не является импликацией, то немножко постаравшись, я уверен, Вы его найдёте. И он будет красивым и убедительным. Человеческий язык — штука чрезвычайно гибкая и многозначная, и поэтому за свою уверенность в том, что «если-то» всегда является импликацией, я не поставил бы ни цента.
. Есть истинность/ложность входящих в импликацию аргументов, а есть истинность/ложность самой импликации.
Что в этом тонкого? Это достойно Капитана Очевидность.
Дальше у Вас, простите, лирика, а не логика.
то немножко постаравшись, я уверен, Вы его найдёте
Я его нашёл и Вам продемонстрировал. Более того, я сформулировал общий критерий, которому должно соответствовать такое отношение.
Это достойно Капитана ОчевидностьА вот ни фига подобного. Берём, например, предубеждение «негры ленивые и бестолковые», которое сразу приводим к каноническому виду «если человек является представителем негроидной расы, то он ленивый и бестолковый». Дальше классика. Находим ленивого и бестолкового негра, А=true, B=true, считаем А→B по правилам булевой алгебры, и получаем true. Ну вот, видали? Я же говорил! Негры ленивые и бестолковые! А что? Всё по науке сделано!
По булевой алгебре всё зашибись: А=true, B=true, А→B=true. А по классической логике налицо логическая ошибка «подтверждение консеквента».
А можно зайти с другой стороны. Найти трудолюбивого и толкового белого, и получить А=false, B=false, А→B=true. Булева алгебра в очередной раз ставит знак качества, а классическая логика включает красную лампочку «отрицание антецедента».
Если включить телевизор на рекламе или новостях (осторожно! опасно для психического здоровья! соблюдать меры предосторожности!), можно заметить, что на подобную хрень публику там ловят по несколько раз в минуту.
Кстати сказать, эмпирическое наблюдение: как-то так получилось, что прекращение преподавания классической логики в школах и ВУЗах совпало по времени с массовым распространением телевидения. Я ни на что не намекаю. Просто наблюдение.
Я его нашёл и Вам продемонстрировалОн меня не убедил. Значит, он недостаточно убедительный. Можете поискать ещё, а можете и забить на это дело. Всё равно я с Вами уже согласился.
Данная классика очевидно выражается при добавлении терминов множеств.
М — множество смертных
Р — множество людей
S — Сократ.
(Р является подмножеством М) AND (S входит в Р) -> S входит в М
Но вопрос всё равно остаётся открытым, потому что я что-то не слышал, чтобы исчисление предикатов кто-то применял в повседневной жизни, то есть за пределами узкоспециализированных дел типа доказательства математических теорем.
Мне кажется, если фантазировать о возвращении логики в общество, имеет смысл говорить о классике, а не об исчислении предикатов.
Классическая логика легко и честно представляется в логике предикатов. В логике высказываний внутренняя структура высказываний не рассматривается, что сильно ограничивает ее применимость. При этом обе используют булеву алгебру для логических операций.
2. Мне оно не преподавалось ни в школе, ни в техническом ВУЗе. Моему сыну оно не преподавалось ни в школе, ни на естественнонаучной специальности в МГУ.
3. Исчисление предикатов также не преподавалось ни мне, ни моему сыну. Ни в школе, ни в ВУЗе.
4. Исчисление предикатов наверняка преподаётся математикам, но много ли их вокруг нас, специалистов-математиков?
5. Формулы исчисления предикатов весьма неудобны для использования ширнармассами в повседневной жизни.
6. Классическая логика гораздо проще и нагляднее. Её понятийный аппарат и инструментарий доступны даже гуманитариям и технарям «от сохи».
7. Если подходить к вопросу формально, то классическая логика покрывается связкой «исчисление предикатов + булева алгебра», но реально по жизни эта замена не работает. По факту. По той реальности, которая дана нам в ощущениях.
В языках программирования импликация выражается операцией сравнения
(a → b) = (a <= b)
хозяйке на заметку :)
Что-то не получается. Для импликации нужна решётка (булева алгебра). Где в, скажем, Паскале, решётка, на которой определена операция сравнения?
Не знаю приём тут вообще решётки, но вот вам немного Паскаля:
writeln(false <= false); {TRUE}
writeln(false <= true); {TRUE}
writeln(true <= false); {FALSE}
writeln(true <= true); {TRUE}Не знаю приём тут вообще решётки
Да, точно, решётки же недостаточно для импликации, нужна именно булева алгебра.
вот вам немного Паскаля
Да, действительно работает. И это не случайное совпадение: в общем случае произвольной решётки a <= b эквивалентно a and b = a, и (a and b = a) = (a -> b) — теорема исчисления высказываний.
a and b = a
Чёрт! Я понял, зачем в Бейсике есть отдельный оператор импликации…
Насчёт "произвольной" решётки или булевой алгебры это, со всей очевидностью, не так.
Первое и самое главное: булева алгебра не вводит отношение порядка.
В двоичном случае, можно ввести порядок истина > ложь, или истина < ложь, и ничего (кроме лайфхака) от этого не изменится.
В векторном пространстве или булеане множеств отношение порядка вообще резко отличается от отношения над компонентами. Начиная с того, что там уже не 2, а 2^n * n! различных лексикографических порядков (где n — размерность пространства), плюс всякие нетривиальные.
В любом случае, определение импликации A→B ≡ ¬A∨B работает для всех, и не вылазит за пределы булевой алгебры.
Учитывая, что и в решётках, и в булевой алгебре есть операции ∧ и ∨ — один из возможных порядков выглядит естественнее другого.
Ну и выражение (a ≤ b) = (a ∧ b = a) от заданного порядка не зависит, и если определять решётку через ∧ и ∨ — то это вообще будет определением операции ≤.
Опять-таки, вы конечно же можете вводить в векторном пространстве любое отношение порядка — но для решёток обычно как-то принято использовать простое по-координатное сравнение.
Простое покоординатное сравнение с последующей индексо-независимой свёрткой (какой? минимум, максимум, сумма?) не отвечает аксиоматике полного порядка. Либо не отвечает желаемой семантике (мы хотим вывести отношение идентичности из отношения порядка).
Вот вам простой пример: векторы (0,1) и (1,0).
Из соображений симметрии ни один из них не может быть "больше" другого. Следовательно, они "равны". И мы на ровном месте подняли класс эквивалентности. Покомпонентное неравенство при равенстве объектов. Живите теперь с этим.
Или вот: булеан множества {a,b,c}.
{a,b} vs {b,c}
по вашей идее,
{a,b}∩{b,c} = {b} ≠ {a,b} ⇒ ¬({a,b} ⩽ {b,c})
{b,c}∩{a,b} = {b} ≠ {b,c} ⇒ ¬({b,c} ⩽ {a,b})
итого,
либо у нас полный порядок — и мы только что нарушили транзитивность
{a,b} > {b,c} > {a,b},
либо у нас неполный порядок.
Если же мы возьмём лексикографический порядок над векторами (или аналогичный ему над множествами), то нас тоже ждут сюрпризы.
(0,1) < (1,0) < (1,1)
(0,1)→(1,0) = (1,0)
(1,1)→(1,0) = (1,0)
покомпонентная импликация даёт одно и то же, а результат сравнения противоположный.
Да, естественно, я имею в виду, что отношения строгого и нестрогого порядка (и эквивалентности) взаимосвязаны:
(a < b) ⇔ ¬(b ⩽ a)
((a ⩽ b) ∧ (b ⩽ a)) ⇔ (a = b)
А с каких пор решётке требуется полный порядок? Решётка всегда была частично упорядоченным множеством.
Вот вам простой пример: векторы (0,1) и (1,0).
Вот вам простой ответ: (0,1) ∧ (1,0) = (0,0), что не равно ни одному из операндов. Следовательно, эти векторы несравнимы.
Э! Давайте вспомним, для чего мы всё это затеяли.
Для того, чтобы импликацию (всюду определённую!) реализовать через сравнение.
Если в нашей структуре порядок неполный, то этот метод прямо сразу непригоден.
Если в нашей структуре порядок вводится из операций, подобных импликации, то зачем нам дополнительно заниматься обращением этой операции?
Так ведь и операция ≤ точно так же всюду определена, независимо от того, полный там порядок или неполный.
А про импликацию — это уже ваша придумка, сами придумали — сами спорите… А math_coder в том комментарии, на который вы отвечали, сразу написал: импликация только в булевой алгебре есть, а вовсе не в произвольной решетке.
Логика — это вообще ментальный инструмент, который бывает полезен (а бывает, что и нет) тогда, когда типовой сценарий «посмотрел и всё сразу понял» выдаёт либо стабильно неверные, либо бесполезные с практической точки зрения ответы. Либо когда нас пытаются обдурить. В 99% случаев мы логику не включаем, и правильно делаем, потому что это очень медленный, тяжеловесный и противоестественный нашему wetware инструмент.
Очень часто я наблюдаю, как логику абсолютизируют. Типа это какой-то язык Бога. Или ещё какой-нибудь зашквар в духе платоновского мира идей. Не знаю как кто, а я в эти сказки не верю. Мне удобнее рассматривать логику именно как полезную выдумку. Костылик, который мы себе придумали для того, чтобы меньше ошибаться в обманчивых ситуациях. Если, конечно, научились им правильно пользоваться.
Внемли же, чему учит светлая йога!
Но картинки красивые. Кстати, книга Рассела и Уайтхеда действительно толщиной с библию, мне так и не хватило силы воли её читать. Что же они там написали сто лет назад? Они, правда, философы были оба, при всём уважении.
Аксиома не детерминирует ф-цию, потому что с тем же успехом можно взять NOR.
Для вывода следствий это несущественно, можно вывести те же теоремы (например, A·B=B·A), и если вместо точки взять например импликацию, система аксиом (из той же формулы и интерпретации · как →) окажется противоречивой.
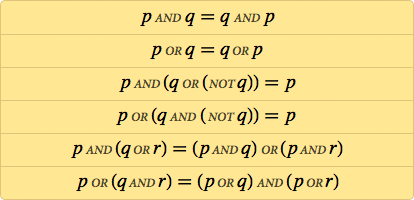
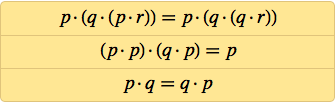
Логика, объяснимость и будущее понимания