How to become an author
Search
Write a publication
Pull to refresh

Фильтр Калмана для минимизации энтропийного значения случайной погрешности с не Гауссовым распределением

Reading time 10 min
Views 9K
Python *Algorithms *Mathematics *Development for Windows *Popular science
Tutorial

Введение


На Habr математическое описание работы фильтра Калмана и особенности его применения рассматривались в следующих публикациях [1÷10]. В публикации [2] в простой и доходчивой форме рассмотрен алгоритм работы фильтра Калмана (ФК) в модели «пространства состояний», Следует отметить, что исследование систем контроля и управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа [11].

Публикация [8] представляет значительный интерес именно для обучения. Очень эффективен методический приём автора, который начал свою статью с рассмотрения распределения случайной погрешности Гаусса, рассмотрел алгоритм ФК и закончил простой итерационной формулой для подбора коэффициента усиления ФК. Автор ограничился рассмотрением распределения Гаусса мотивируя это тем, что при достаточно больших $n$ (многократных измерений) закон распределения суммы случайных величин стремится к распределению Гаусса.

Теоретически такое утверждение, безусловно, справедливо, однако на практике число измерений в каждой точке диапазона не может быть очень большим. Сам R. E. Kalman получил результаты о минимуме ковариации фильтра на базе ортогональных проекций, без предположения о гауссовости ошибок измерений [12].

Целью настоящей публикации является исследование возможностей фильтра Калмана для минимизации энтропийного значения случайной погрешности с не Гауссовым распределением.
Для оценки эффективности фильтра Калмана при идентификации закона распределения или суперпозицией законов по экспериментальным данным воспользуемся информационная теорией измерений основанной на теории информации К. Шеннона, согласно которой информация, подобно физической величине, может быть измерена и оценена.

Основное достоинство информационного подхода к описанию измерений состоит в том, что размер энтропийного интервала неопределенности может быть найден строго математически для любого закона распределения. Что устраняет исторически сложившийся произвол, неизбежный при волевом назначении различных значений доверительной вероятности.Это особенно важно и в учебном процессе, когда обучающий может наблюдать уменьшение неопределённости измерений при применении фильтрации Калмана на заданной ему числовой выборке[13,14].

Кроме того, по совокупности вероятностных и информационных характеристикам выборки можно более точно определить характер распределения случайной погрешности. Это объясняется обширной базой численных значений таких параметров, как энтропийный коэффициент и контрэксцесс для различных законов распределения и их суперпозицией.

Оценка суперпозиции законов распределения случайной величины по энтропийному коэффициенту и контрэксцессу (полученных из экспериментальных данных)

Плотность распределения вероятностей для каждого столбца гистограммы [14] шириной $d$ равна $p_{i}(x_{i})=n_{i}/(n\cdot d) $, отсюда оценка вероятностей энтропии определяется как $H\left (x\right)= \int_{-\infty }^{+\infty}p\left ( x\right)\ln p\left (x\right )dx$ при нахождении энтропии по гистограмме из $m $ столбцов получим соотношение:

$\displaystyle H\left (x\right )= -\sum_{i=1}^{m}\int_{\tilde{x_{i}}-\frac{d}{2}}^{\tilde{x_{i}}+\frac{d}{2}}\frac{n_{i}}{nd}\ln\frac{n_{i}}{nd} =\sum_{i=1}^{m}\frac{n_{i}}{n}\ln \frac{n}{n_{i}}+\ln d$

Представим выражение для оценки энтропии в виде:

$H\left (x\right )= \ln \left [ d\prod_{i=1}^{m}\left (\frac{n}{n_{i}} \right)^{\frac{n_{i}}{n}}\right ]$

Получим выражение для оценки энтропийного значения случайной величины:

$\Delta _{e}= \frac{1}{2}e^{H\left (x\right )}=\frac{dn}{2}10^{-\frac{1}{n}\sum_{1}^{m}n_{i}\lg n_{i}} $

Классификацию законов распределения осуществляют на плоскости в координатах энтропийного коэффициента $k=\frac{\Delta _{e}}{\sigma}$ и контрэксцесса $\psi =\frac{\sigma ^{2}}{\sqrt{\mu _{4}}}$ где $\mu _{4}=\frac{1}{n}\sum_{1}^{n}\left ( x_{i}-\bar{X} \right )^{4}$.

Для всех возможных законов распределения \psi изменяется от 0 до 1, а k от 0 до 2,066, поэтому каждый закон может характеризоваться некоторой точкой. Покажем это, используя следующую программу:

Плоскость законов распределения
import matplotlib.pyplot as plt
from numpy import*
from scipy.stats import *
def graf(a):#группировка данных
         a.sort()
         n=len(a)
         m= int(10+sqrt(n))
         d=(max(a)-min(a))/m
         x=[];y=[]
         for i in arange(0,m,1):
                  x.append(min(a)+d*i)
                  k=0
                  for j in a:
                           if min(a)+d*i <=j<min(a)+d*(i+1):
                                    k=k+1
                  y.append(k)
         h=(1+0.5*m/n)*0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)     
         k=h/std (a)
         mu4=sum ([(w-mean (a))**4 for w in a])/n
         psi=(std(a))**2/sqrt(mu4)
         return  psi,k
b=800#объём контрольной выборки
plt.title('Плоскость законов распределения', size=12)
plt.xlabel('Коэффициент $\psi$', size=12)
plt.ylabel('Энтропийный коэффициент k', size=12)
a=uniform.rvs( size=b)
psi,k,=graf(a)
nr="Равномерное : k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',  label=nr)
a=logistic.rvs( size=b)
psi,k,=graf(a)
nr="Логистическое:k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',  label=nr)
a=norm.rvs( size=b)
psi,k,=graf(a)
nr="Нормальное :K=%s,$\psi$i=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',   label=nr)
a= erlang.rvs(4,size=b)
psi,k,=graf(a)
nr=" Эрланга :k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k, 'o',  label=nr)
a= pareto.rvs(4,size=b)
psi,k,=graf(a)
nr="Парето :k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k, 'o',  label=nr)
a = cauchy.rvs(size=b)
psi,k,=graf(a)
nr="Коши :k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',   label=nr)
c = 0.412
a = genlogistic.rvs(c, size=b)
psi,k,=graf(a)
nr="Логистическое -1:k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',   label=nr)
mu=0.6
a = poisson.rvs(mu, size=b)
psi,k,=graf(a)
nr="Пуассона:k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',   label=nr)
a= laplace.rvs(size=b)
psi,k,=graf(a)
nr="Лапласа:k=%s,$\psi$=%s "%(round(k,3),round(psi,3))
plt.plot(psi,k,'o',   label=nr)
plt.legend(loc='best')
plt.grid()
plt.show()




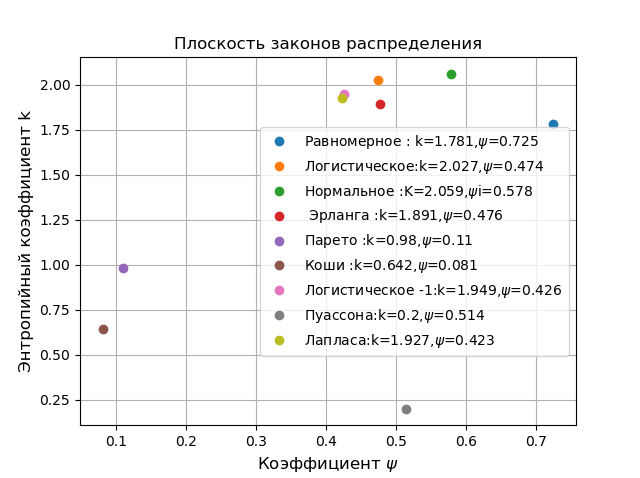
На плоскости в координатах $k,\psi$ удалены от остальных распределений, распределения Парето, Коши хотя они и относятся к разным областям применения первое в физике а второе в экономике. Для сравнения следует выбрать находящееся в вершине классификации нормальное распределение Гаусса. Все приведенные ниже сравнения выполняются на ограниченной выборке и носят характер демонстрации возможностей ФК на примере численного определения энтропийной погрешности.

Выбор алгоритма фильтра Калмана


В каждой выбранной точке диапазона измерений проводятся многократные измерения и их результат сравнивается с мерой которую ФК «не знает». Поэтому следует выбрать ФК, например Kalman Filter to Estimate a Constant [16]. Однако я предпочитаю Python и остановился на варианте [16] с обширной документацией. Приведу описание алгоритма:

Поскольку константа всегда одна модель системы можно представить в виде:

$x_{k}=x_{k-1}+w_{k}$, (1)

Для модели матрица перехода вырождается в единицу, а матрица управления в ноль.Модель измерения примет вид:

$y_{k}=y_{k-1}+v_{k}$, (2)

Для модели (2) матрица измерений превращаются в единицу, а ковариационные матрицы $P,Q,R$ превращаются в дисперсии.На очередном $k$-м шаге, до прихода результатов измерения, скалярный фильтр Калмана пытается по формуле (1) оценить новое состояние системы:

$\hat{x}_{k/(k-1)}=\hat{x}_{(k-1)/(k-1)}$, (3)

Уравнение (3) показывает, что априорная оценка на следующем шаге равна апостериорной оценке, сделанной на предыдущем шаге. Априорная оценка дисперсии ошибки:

$ P_{k/(k-1)}=P_{(k-1)/(k-1)}+Q_{k}$, (4)

По априорной оценке состояния $\hat{x}_{k/(k-1)} $ можно вычислить прогноз измерения:

$\hat{y}_{k}=\hat{x}_{k/(k-1)}$, (5)

После того, как получено очередное измерение $ y_{k}$, фильтр рассчитывает ошибку своего прогноза $k$-го измерения:

$ e_{k}=y_{k}-\hat{y}_{k}=y_{k}-\hat{x}_{k/(k-1)} $, (6)

Фильтр корректирует свою оценку состояния системы, выбирая точку, лежащую где-то между первоначальной оценкой $\hat{x}_{k/(k-1)} $и точкой, соответствующей новому измерению $y_{k}$:

$e_{k}=y_{k}-\hat{y}_{k}=y_{k}-\hat{x}_{k/(k-1)}$, (7)

где $G _{k} $— коэффициент усиления фильтра.

Также корректируется оценка дисперсии ошибки:

$P_{k/(k)}=(1-G_{k})\cdot P_{k/(k-1)}$, (8)

Можно доказать, что дисперсия ошибки $e_{k}$ равна:

$S_{k}=P_{k/(k-1)}+R_{k}$, (9)

Коэффициент усиления фильтра, при котором достигается минимальная ошибка оценки состояния системы определяется из соотношения:

$G_{k}=P_{k/(k-1)}/S_{k}$, (10)

Минимизация энтропийной погрешности ФК для шумов с распределением Коши, Парето и Гаусса

1. В теории вероятности плотность распределения Коши определяется из соотношения:

$f(x)=\frac{b}{\pi\cdot (1-x^{2})}$

Для этого распределения невозможно оценить погрешность методами теории вероятности ($\sigma =\infty$) но информационная теория позволяет это сделать:

Программа минимизации ФК энтропийной погрешности от шумов Коши
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import *
def graf(a):#группировка данных для определения энтропийной погрешности
         a.sort()
         n=len(a)
         m= int(10+sqrt(n))
         d=(max(a)-min(a))/m
         x=[];y=[]
         for i in arange(0,m,1):
                  x.append(min(a)+d*i)
                  k=0
                  for j in a:
                           if min(a)+d*i <=j<min(a)+d*(i+1):
                                    k=k+1
                  y.append(k)
         h=(1+0.5*m/n)*0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)         
         return  h
def Kalman(a,x,sz,R1):
    R = R1*R1  # Дисперсия    
    Q = 1e-5 # Дисперсия случайной величины в модели системы 
    # Выделение памяти под массивы:
    xest1 = zeros(sz)  # Априорная оценка состояния
    xest2 = zeros(sz)  # Апостериорная оценка состояния  
    P1 = zeros(sz)     # Априорная  оценка ошибки  
    P2 = zeros(sz)     # Апостериорная оценка ошибки  
    G = zeros(sz)      # Коэффициент усиления фильтра
    xest2[0] = 0.0
    P2[0] = 1.0
    for k in arange(1, sz): # Цикл по отсчётам времени. 
             xest1[k] = xest2[k-1] # Априорная оценка состояния. 
             P1[k] = P2[k-1] + Q# Априорная оценка ошибки.
             # После получения нового значения измерения вычисляем апостериорные оценки : 
             G[k] = P1[k] / ( P1[k] + R )
             xest2[k] = xest1[k] + G[k] * ( a[k] - xest1[k] )
             P2[k] = (1 - G[k]) * P1[k]
    return  xest2,P1
nr="распределением Коши "
x =2# Истинное значение измеряемой величины фильтру неизвестно)
R1 = 0.1  # Ср . кв . ошибка измерения . 
sz = 50   # Число итераций.
a = cauchy.rvs(x, R1, size=sz)
xest2,P1=Kalman(a,x,sz,R1)
plt.plot(a, 'k+', label='Зашумлённые измерения')
plt.plot(xest2,'b-', label='Апостериорная оценка')
plt.axhline(x, color='g', label='Истинное значение')
plt.axis([0, sz,-x, 2*x])
plt.legend()
plt.xlabel('Номер итерации')
plt.ylabel(u'Измеряемая величина')
h1=graf(a)
h2=graf(xest2)
plt.title('Подавление шумов с %s.\n Энтропийная погрешность до ФК $\Delta $1=%s после ФК $\Delta $2=%s '%(nr,round(h1,3),round(h2,3)), size=12)
plt.grid()
plt.show()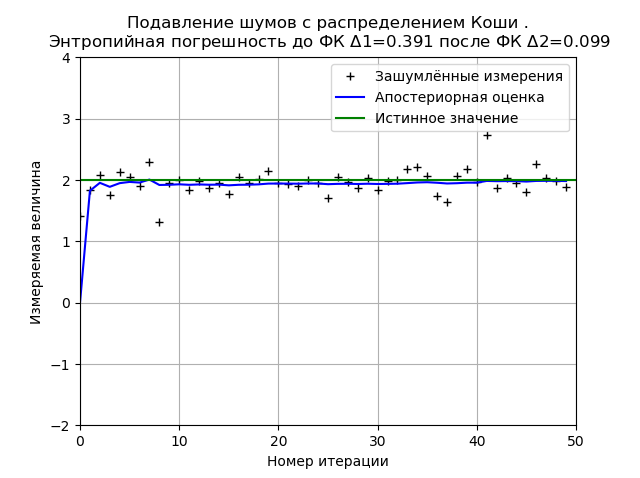




Вид графика может изменяться как при перезагрузке программы(новой генерации выборки распределения), так и в зависимости от числа измерений и параметров распределения, но одно останется неизменным ФК минимизирует значение энтропийной погрешности вычисленной на основе информационной теории измерений. Для приведенного графика ФК снижает энтропийную погрешность в 3,9 раза.

2. В теории вероятности плотность распределения Парето с параметрами $x_{m}$ и $k$ определяется из соотношения:

$f_{X}(x)= \left\{\begin{matrix} \frac{kx_{k}^{m}}{x^{k+1}},& x\geq x_{m}\\ 0,& x< x_{m} \end{matrix}\right. $



Следует отметить, что распределение Парето встречается не только в экономике. Можно привести следующий пример распределение размера файла в интернет-трафике по TCP-протоколу.

3. В теории вероятности плотность нормального распределения (Гаусса) с математическим ожиданием $\mu$ и среднеквадратическим отклонением $\sigma$ определяется из соотношения:

$f(x)=\frac{1}{\sigma \sqrt{2\pi}}\cdot e^{-\frac{(x-\mu)^{2}}{2\sigma ^{2}}}$

Определение минимизации ФК энтропийной погрешности от шумов с распределением Гаусса приводим для сравнения с не Гауссовыми распределениями Коши и Парето.

Программа минимизации ФК энтропийной погрешности от шумов нормального распределения
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import *
def graf(a):#группировка данных для определения энтропийной погрешности
         a.sort()
         n=len(a)
         m= int(10+sqrt(n))
         d=(max(a)-min(a))/m
         x=[];y=[]
         for i in arange(0,m,1):
                  x.append(min(a)+d*i)
                  k=0
                  for j in a:
                           if min(a)+d*i <=j<min(a)+d*(i+1):
                                    k=k+1
                  y.append(k)
         h=(1+0.5*m/n)*0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)         
         return  h
def Kalman(a,x,sz,R1):
    R = R1*R1  # Дисперсия    
    Q = 1e-5 # Дисперсия случайной величины в модели системы 
    # Выделение памяти под массивы:
    xest1 = zeros(sz)  # Априорная оценка состояния
    xest2 = zeros(sz)  # Апостериорная оценка состояния  
    P1 = zeros(sz)     # Априорная  оценка ошибки  
    P2 = zeros(sz)     # Апостериорная оценка ошибки  
    G = zeros(sz)      # Коэффициент усиления фильтра
    xest2[0] = 0.0
    P2[0] = 1.0
    for k in arange(1, sz): # Цикл по отсчётам времени. 
             xest1[k] = xest2[k-1] # Априорная оценка состояния. 
             P1[k] = P2[k-1] + Q# Априорная оценка ошибки.
             # После получения нового значения измерения вычисляем апостериорные оценки : 
             G[k] = P1[k] / ( P1[k] + R )
             xest2[k] = xest1[k] + G[k] * ( a[k] - xest1[k] )
             P2[k] = (1 - G[k]) * P1[k]
    return  xest2,P1
nr="распределением Гаусса "
x =2# Истинное значение измеряемой величины фильтру неизвестно)
R1 = 0.1  # Ср . кв . ошибка измерения . 
sz = 50   # Число итераций.
a=norm.rvs( x, R1, size=sz)
xest2,P1=Kalman(a,x,sz,R1)
plt.plot(a, 'k+', label='Зашумлённые измерения')
plt.plot(xest2,'b-', label='Апостериорная оценка')
plt.axhline(x, color='g', label='Истинное значение')
plt.axis([0, sz,-x, 2*x])
plt.legend()
plt.xlabel('Номер итерации')
plt.ylabel(u'Измеряемая величина')
h1=graf(a)
h2=graf(xest2)
plt.title('Подавление шумов с %s.\n Энтропийная погрешность до ФК $\Delta $1=%s после ФК $\Delta $2=%s '%(nr,round(h1,3),round(h2,3)), size=12)
plt.grid()
plt.show()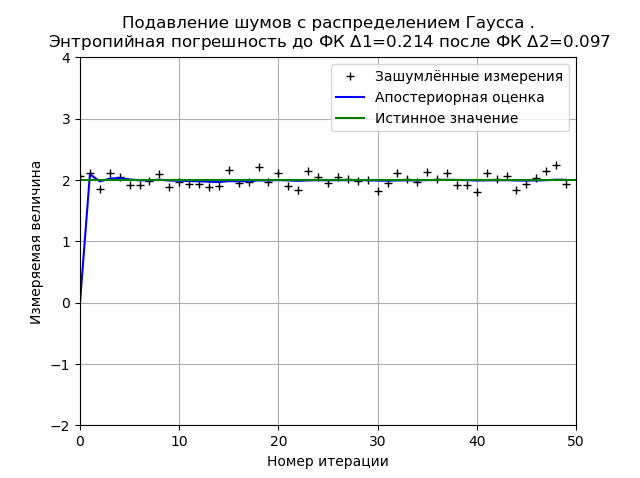




Распределение Гаусса обеспечивает более высокую стабильность результата при 50 измерениях и для приведенного графика энтропийная погрешность уменьшается в 2,2 раза.

Минимизация ФК энтропийной погрешности по выборке экспериментальных данных с неизвестным законом распределения шумов

Программа минимизации ФК энтропийной погрешности ограниченной выборки экспериментальных данных
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import *
def graf(a):#группировка данных для определения энтропийной погрешности
         a.sort()
         n=len(a)
         m= int(10+sqrt(n))
         d=(max(a)-min(a))/m
         x=[];y=[]
         for i in arange(0,m,1):
                  x.append(min(a)+d*i)
                  k=0
                  for j in a:
                           if min(a)+d*i <=j<min(a)+d*(i+1):
                                    k=k+1
                  y.append(k)
         h=(1+0.5*m/n)*0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)
         k=h/std (a)
         mu4=sum ([(w-mean (a))**4 for w in a])/n
         psi=(std(a))**2/sqrt(mu4)
         return  h
def Kalman(a,x,sz,R1):
    R = R1*R1  # Дисперсия    
    Q = 1e-5 # Дисперсия случайной величины в модели системы 
    # Выделение памяти под массивы:
    xest1 = zeros(sz)  # Априорная оценка состояния
    xest2 = zeros(sz)  # Апостериорная оценка состояния  
    P1 = zeros(sz)     # Априорная  оценка ошибки  
    P2 = zeros(sz)     # Апостериорная оценка ошибки  
    G = zeros(sz)      # Коэффициент усиления фильтра
    xest2[0] = 0.0
    P2[0] = 1.0
    for k in arange(1, sz): # Цикл по отсчётам времени. 
             xest1[k] = xest2[k-1] # Априорная оценка состояния. 
             P1[k] = P2[k-1] + Q# Априорная оценка ошибки.
             # После получения нового значения измерения вычисляем апостериорные оценки : 
             G[k] = P1[k] / ( P1[k] + R )
             xest2[k] = xest1[k] + G[k] * ( a[k] - xest1[k] )
             P2[k] = (1 - G[k]) * P1[k]
    return  xest2,P1

R1 = 0.9  # Ср . кв . ошибка измерения . 
a=[ 0.203, 0.154, 0.172, 0.192, 0.233, 0.181, 0.219, 0.153, 0.168, 0.132, 0.204, 0.165, 0.197, 0.205, 0.143,   0.201, 0.168, 0.147, 0.208, 0.195, 0.153, 0.193, 0.178, 0.162, 0.157, 0.228, 0.219, 0.125, 0.101, 0.211,0.183, 0.147,    0.145, 0.181,0.184, 0.139, 0.198, 0.185, 0.202, 0.238, 0.167, 0.204, 0.195, 0.172, 0.196, 0.178, 0.213, 0.175, 0.194,   0.178, 0.135, 0.178, 0.118, 0.186, 0.191]
sz = len(a)   # Число итераций
x =0.179# Истинное значение измеряемой величины фильтру неизвестно)
xest2,P1=Kalman(a,x,sz,R1)
plt.plot(a, 'k+', label='Зашумлённые измерения')
plt.plot(xest2,'b-', label='Апостериорная оценка')
plt.axhline(x, color='g', label='Истинное значение')
plt.axis([0, sz,-x, 2*x])
plt.legend()
plt.xlabel('Номер итерации')
plt.ylabel('Измеряемая величина')
h1=graf(a)
nr=" неизвестным распределением"
h2=graf(xest2)
plt.title('Подавление шумов с %s \n Энтропийная погрешность до ФК $\Delta $1=%s после ФК $\Delta $2=%s '%(nr,round(h1,3),round(h2,3)), size=12)
plt.grid() 
plt.show()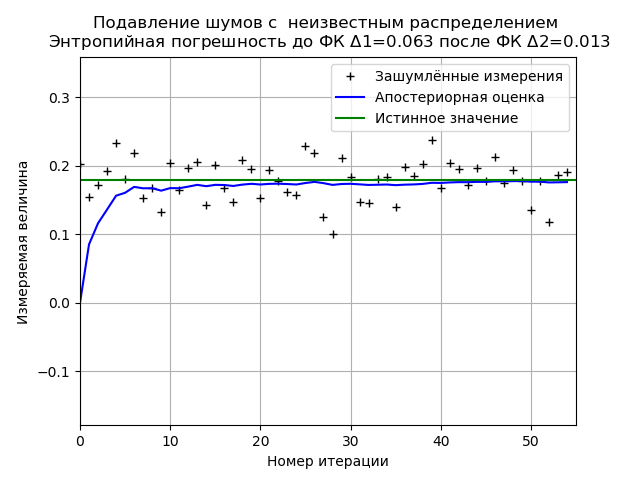




При анализе выборки экспериментальных данных получаем стабильные результаты по минимизации ФК энтропийной погрешности. Для данной выборки ФК уменьшает энтропийную погрешность в 4,85 раза.

Вывод


Все приведенные в данной статье сравнения проводились на ограниченных выборках данных, поэтому от основополагающих выводов следует воздержаться, однако использование энтропийной погрешности позволяет количественно оценить эффективность фильтра Калмана в приведенной реализации, поэтому учебную задачу данной статьи можно считать выполненной.

Ссылки
1. Неортогональная БИНС для малых БПЛА
2. Фильтр Калмана — !cложно?
3. Без запаха фильтрации и нелинейного оценивания *
4. На пороге дополненной реальности: к чему готовиться разработчикам (часть 2 из 3)
5. Классическая механика: о диффурах «на пальцах»
6. Фильтр Калмана — Введение
7. Генератор Федеративного Фильтра Калмана с использованием Генетических Алгоритмов.
8. Фильтр Калмана
9. Использование фильтра Калмана для определения производных измеряемой величины
10. Простая модель адаптивного фильтра Калмана средствами Python
11. Пространство состояний в задачах проектирования систем оптимального управления
12. A New Approach to Linear Filtering and Prediction Problems1
13. Вероятностный и информационный анализ результатов измерений на Python
14. Подбор закона распределения случайной величины по данным статистической выборки средствами Python
15. Kalman filtering
16. Kalman Filter to Estimate a Constant
Tags:
Hubs:
+33
Comments 17
70
Karma
0
Rating
Юрий Тараненко @Scorobey

Разработчик учебных программ

Send message
Comments Comments 17

Articles

Unlock dark mode

Your account

Sections

Information

Services

Support
© 2006–2024, Habr