Comments 17
1. Не могли бы вы детально рассказать как вы перешли от дискретной энтропии H=-sum(p*ln(p)) с суммой безразмерных величин, к интегрированию плотности распределения случайной величины с размерными величинами под логарифмом?
2. Почему у вас постоянно пропадают знаки, то энтропии, то в распределении Коши.
3. И какое отношение «энтропийная погрешность» имеет отношение к погрешности измерения?
4. Не кажется ли вам что в учебных материалах, надо определять все величины по ходу пьесы, а не ссылать в список литературы без приведения минимально информации из неё необходимой для дальнейшего объяснения.
5. Что бы «учебную задачу данной статьи можно считать выполненной» эту задачу следовало бы хотя бы определить. А так получили какие то не ведомые цифры ни имеющие вообще никакого отношения ни к какой практической задаче.
ps: Ваше рвение писать наукообразные статьи похвально. Но пока получается не очень.
2. Почему у вас постоянно пропадают знаки, то энтропии, то в распределении Коши.
3. И какое отношение «энтропийная погрешность» имеет отношение к погрешности измерения?
4. Не кажется ли вам что в учебных материалах, надо определять все величины по ходу пьесы, а не ссылать в список литературы без приведения минимально информации из неё необходимой для дальнейшего объяснения.
5. Что бы «учебную задачу данной статьи можно считать выполненной» эту задачу следовало бы хотя бы определить. А так получили какие то не ведомые цифры ни имеющие вообще никакого отношения ни к какой практической задаче.
ps: Ваше рвение писать наукообразные статьи похвально. Но пока получается не очень.
0
«1. Не могли бы вы детально рассказать как вы перешли от дискретной энтропии H=-sum(p*ln(p)) с суммой безразмерных величин, к интегрированию плотности распределения случайной величины с размерными величинами под логарифмом?»
Рассказывать о том что относительные величины не имеют размерности не нужно, это и так понятно.!
«2. Почему у вас постоянно пропадают знаки, то энтропии, то в распределении Коши.»
Правило логарифма отношения величин изучают в школе ln(a/b)=-ln(b/a)
«3.И какое отношение «энтропийная погрешность» имеет отношение к погрешности измерения?»
Энтропийная погрешность измерений одна из форм представления погрешности измерений. Школьная программа по информатике.
«4.Не кажется ли вам что в учебных материалах, надо определять все величины по ходу пьесы, а не ссылать в список литературы без приведения минимально информации из неё необходимой для дальнейшего объяснения.»
Пьесу смотрят, а объяснение элементарных вещей мешает просмотру. Методика расчета энтропийной погрешности приведена подробно и без ссылок на литературу.
«5. Что бы «учебную задачу данной статьи можно считать выполненной» эту задачу следовало бы хотя бы определить. А так получили какие то не ведомые цифры ни имеющие вообще никакого отношения ни к какой практической задаче.»
Учебная задача поставлена в статье — это обработка экспериментальных данных методами информационной теории измерений с минимизацией энтропийной погрешности при помощи фильтра Калмана.
Снижение погрешность измерений самая актуальная практическая задача. При этом какие то неведомые цифры( по Вашему определению)" характеризуют энтропийную погрешность в полном соответствии с информационной теорией измерений.
ps. Ваше рвение писать наукообразные комментарии похвально. Но пока получается не очень.
Рассказывать о том что относительные величины не имеют размерности не нужно, это и так понятно.!
«2. Почему у вас постоянно пропадают знаки, то энтропии, то в распределении Коши.»
Правило логарифма отношения величин изучают в школе ln(a/b)=-ln(b/a)
«3.И какое отношение «энтропийная погрешность» имеет отношение к погрешности измерения?»
Энтропийная погрешность измерений одна из форм представления погрешности измерений. Школьная программа по информатике.
«4.Не кажется ли вам что в учебных материалах, надо определять все величины по ходу пьесы, а не ссылать в список литературы без приведения минимально информации из неё необходимой для дальнейшего объяснения.»
Пьесу смотрят, а объяснение элементарных вещей мешает просмотру. Методика расчета энтропийной погрешности приведена подробно и без ссылок на литературу.
«5. Что бы «учебную задачу данной статьи можно считать выполненной» эту задачу следовало бы хотя бы определить. А так получили какие то не ведомые цифры ни имеющие вообще никакого отношения ни к какой практической задаче.»
Учебная задача поставлена в статье — это обработка экспериментальных данных методами информационной теории измерений с минимизацией энтропийной погрешности при помощи фильтра Калмана.
Снижение погрешность измерений самая актуальная практическая задача. При этом какие то неведомые цифры( по Вашему определению)" характеризуют энтропийную погрешность в полном соответствии с информационной теорией измерений.
ps. Ваше рвение писать наукообразные комментарии похвально. Но пока получается не очень.
-1
1. Плотность распределения имеет размерность 1/dx
2. К логарифмам претензий нет.


3. Энтропия это мера количества информации/состояний системы. А что такое энтропийная погрешность в вашем случае.
4. Если вы пишете учебный материал. Те кто его пытаются читать должны получать информацию последовательно, без разрывов. (Хорошо бы еще полезную). Так что бы не нужно было лазить по ссылкам что бы понять что обозначают буквы которыми вы оперируете. Из ссылок надо приводить минимальную информацию, достаточную для дальнейшего чтения вашего материала без лазания по ссылке.
«Методика расчета энтропийной погрешности приведена» — где она приведена, только в коде на питоне где вы разбиваете область значений на 17 интервалов?
Интересует не как определена энтропийная погрешность (математически не корректно), а какой смысл в её вычислении и почему вы её пытаетесь использовать.
Извините какая цель? Убрать плац с помощью лома? Тут важен сам процесс?
Вы можете оценить погрешность измерения. Оценить распределение ошибок и т.п.
Но практическая задача снижения погрешности лежит совсем в другой области. Для более точного измерения величины нужны более точные приборы, большая статистика или иные методы измерения.
Если умножить погрешность на 1/10 погрешность уменьшиться, а если на 0 так вообще пропадёт. Но какой толк от этих операций? Нам же нужна сама величина и доверительный интервал. Какой смысл «заверать» ошибку измерения?
2. К логарифмам претензий нет.


3. Энтропия это мера количества информации/состояний системы. А что такое энтропийная погрешность в вашем случае.
4. Если вы пишете учебный материал. Те кто его пытаются читать должны получать информацию последовательно, без разрывов. (Хорошо бы еще полезную). Так что бы не нужно было лазить по ссылкам что бы понять что обозначают буквы которыми вы оперируете. Из ссылок надо приводить минимальную информацию, достаточную для дальнейшего чтения вашего материала без лазания по ссылке.
«Методика расчета энтропийной погрешности приведена» — где она приведена, только в коде на питоне где вы разбиваете область значений на 17 интервалов?
Интересует не как определена энтропийная погрешность (математически не корректно), а какой смысл в её вычислении и почему вы её пытаетесь использовать.
Учебная задача поставлена в статье — это обработка экспериментальных данных методами информационной теории измерений с минимизацией энтропийной погрешности при помощи фильтра Калмана.
Извините какая цель? Убрать плац с помощью лома? Тут важен сам процесс?
Снижение погрешность измерений самая актуальная практическая задача.
Вы можете оценить погрешность измерения. Оценить распределение ошибок и т.п.
Но практическая задача снижения погрешности лежит совсем в другой области. Для более точного измерения величины нужны более точные приборы, большая статистика или иные методы измерения.
Если умножить погрешность на 1/10 погрешность уменьшиться, а если на 0 так вообще пропадёт. Но какой толк от этих операций? Нам же нужна сама величина и доверительный интервал. Какой смысл «заверать» ошибку измерения?
0
Как известно, погрешность имеет две составляющие: систематическую и случайную, фильтрация уменьшает случайную составляющую, именно для этого и применяется фильтр Калмана. Энтропийная форма представления погрешности отображает интервал неопределённости (не путайте с доверительным интервалом). По Вашему мнению, применение фильтра не снижает случайную составляющую погрешности, обусловленную наличием шумов — Вы это серьёзно?!.. Разберитесь с терминологией…
0
Каких шумов? У вас есть шум в виде наводок 50Гц? У вас есть физическая модель системы — константа. Т.е. грубо вы линейкой измеряете длину 55 раз. Систематическая погрешность равна разрешающей способности линейки, а случайная зависит от факторов которые вам не подвластным (влажность, температура, внутренняя структура и т.п.). Вы оцениваете дисперсию полученных значений, умножаете на коэффициент (определяющий вероятность попасть в доверительный интервал) и на основе этих цифр получаете доверительный интервал.
«Энтропийная форма представления погрешности отображает интервал неопределённости» — откуда и куда отображает?
Фильтры есть разные и они предназначены для подавления разного рода помех. Но для этого надо иметь модель помех или модель процесса.
«Энтропийная форма представления погрешности отображает интервал неопределённости» — откуда и куда отображает?
Фильтры есть разные и они предназначены для подавления разного рода помех. Но для этого надо иметь модель помех или модель процесса.
-1
Фильтр Калмана в каждом цикле корректирует дисперсию, и, при многократных измерениях, дисперсия случайной величины уменьшается, а следовательно сужается интервал неопределённости и уменьшается энтропийная погрешность. Закон распределения случайной погрешности определяется по энтропийному коэффициенту и контрэксцессу и не зависит от физической природы случайной величины.
+1
Вы не можете менять дисперсию случайной величины. Вы можете только оценить её величину (закон распределения).
0
«Вы не можете менять дисперсию случайной величины. Вы можете только оценить её величину (закон распределения).»
Да нужно говорить об оценке дисперсии для ограниченной выборки по которой мы её определяем, но это не как не влияет на факт уменьшения оценки дисперсии при использовании фильтра Калмана в режиме многократных измерений.
Да нужно говорить об оценке дисперсии для ограниченной выборки по которой мы её определяем, но это не как не влияет на факт уменьшения оценки дисперсии при использовании фильтра Калмана в режиме многократных измерений.
+1
Усреднение результатов многократных наблюдений при постоянстве значения измеряемой величины является наиболее эффективным методом уменьшения случайной погрешности измерения. При проведении многократных (n) наблюдений одного и того же значения физической величины во многих случаях в качестве результата измерения выбирается среднее значение результатов наблюдений. В этом случае среднее квадратическое отклонение результата измерения уменьшается в n раз.
0
Уточняю: В этом случае среднее квадратическое отклонение результата измерения уменьшается в корень квадратный из n
0
А вы проверьте:
Оценка дисперсии не зависит от n, она сходится к значению дисперсии случайной величины, но никак не уменьшается.
import scipy.stats
from random import normalvariate
class Disp:
def __init__(self):
self.m=0
self.d=0
self.n=0
def add(self,x):
self.n=self.n+1
if self.n>1:
self.d=self.d*(self.n-2)/(self.n-1)+(x-self.m)**2/self.n
self.m=self.m+(x-self.m)/self.n
def getN(self):
return self.n # =n
def getM(self):
return self.m # =sum(x[i])/n
def getD(self):
return self.d # =sum((x[i]-m)^2)/(n-1)
def st(alpha,n):
return scipy.stats.t.ppf((1+alpha)/2, n-1)
disp=Disp()
xo=1
mu=0.5
print("Estimate xsi(xo=%.2f,mu=%.2f)\n"%(xo,mu))
alpha=0.95
print(" count xsi mean disp err(%.2f)"%alpha)
j=10
for i in range(100000):
y=normalvariate(xo,mu)
disp.add(y)
if i+1==j:
j=j*10
n,m,d=disp.getN(),disp.getM(),disp.getD()**0.5
print("%7d\t%7.4f\t%7.4f\t%7.4f\t%7.4f"%( n, y, m, d, d*st(alpha,n) ))
Estimate xsi(xo=1.00,mu=0.50)
count xsi mean disp err(0.95)
10 0.4935 0.9605 0.5443 1.2313
100 0.8873 1.0034 0.4685 0.9296
1000 1.3086 0.9905 0.4961 0.9734
10000 1.0788 1.0022 0.5023 0.9845
100000 0.8025 0.9999 0.5000 0.9800Оценка дисперсии не зависит от n, она сходится к значению дисперсии случайной величины, но никак не уменьшается.
0
2019 год на дворе, а всё старика Калмана лохматят.
0
Проверяю!
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import norm
n_iter = 100 # Число итераций.
sz = (n_iter,) # Размер массива
x =2# Истинное значение измеряемой величины (фильтру неизвестно)
R1 = 0.1 # Ср. кв. ошибка измерения.
R = R1*R1 # Дисперсия
nr=«нормальным распределением»
y=norm.rvs( x, R1, size=sz)
Q = 1e-5 # Дисперсия случайной величины в модели системы
# Выделение памяти под массивы:
xest1 = zeros(sz) # Априорная оценка состояния
xest2 = zeros(sz) # Апостериорная оценка состояния
P1 = zeros(sz) # Априорная оценка ошибки
P2 = zeros(sz) # Апостериорная оценка ошибки
G = zeros(sz) # Коэффициент усиления фильтра
xest2[0] = 0.0
P2[0] = 1.0
for k in arange(1, n_iter,1): # Цикл по отсчётам времени.
xest1[k] = xest2[k-1] # Априорная оценка состояния.
P1[k] = P2[k-1] + Q# Априорная оценка ошибки.
# После получения нового значения измерения вычисляем апостериорные оценки:
G[k] = P1[k] / ( P1[k] + R )
xest2[k] = xest1[k] + G[k] * ( y[k] — xest1[k] )
P2[k] = (1 — G[k]) * P1[k]
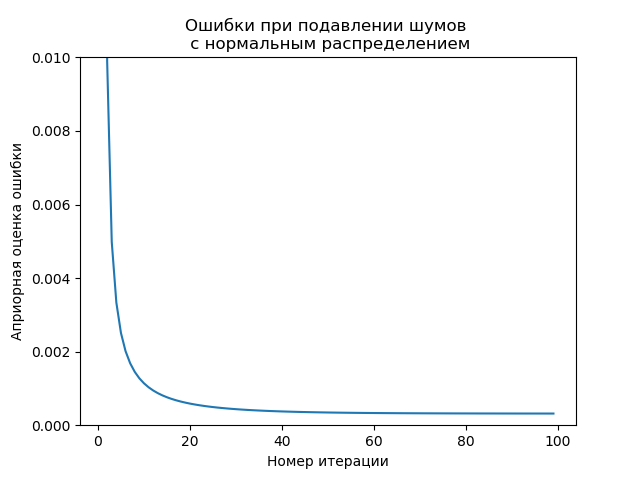
plt.title('Ошибки при подавлении шумов \n с %s'%nr, size=12)
valid_iter = arange(1, n_iter,1) # P1 на 0 м шаге не определено
plt.plot(valid_iter, P1[valid_iter])
plt.xlabel('Номер итерации')
plt.ylabel('Априорная оценка ошибки')
plt.setp(plt.gca(), 'ylim', [0, .01] )
plt.show()
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import norm
n_iter = 100 # Число итераций.
sz = (n_iter,) # Размер массива
x =2# Истинное значение измеряемой величины (фильтру неизвестно)
R1 = 0.1 # Ср. кв. ошибка измерения.
R = R1*R1 # Дисперсия
nr=«нормальным распределением»
y=norm.rvs( x, R1, size=sz)
Q = 1e-5 # Дисперсия случайной величины в модели системы
# Выделение памяти под массивы:
xest1 = zeros(sz) # Априорная оценка состояния
xest2 = zeros(sz) # Апостериорная оценка состояния
P1 = zeros(sz) # Априорная оценка ошибки
P2 = zeros(sz) # Апостериорная оценка ошибки
G = zeros(sz) # Коэффициент усиления фильтра
xest2[0] = 0.0
P2[0] = 1.0
for k in arange(1, n_iter,1): # Цикл по отсчётам времени.
xest1[k] = xest2[k-1] # Априорная оценка состояния.
P1[k] = P2[k-1] + Q# Априорная оценка ошибки.
# После получения нового значения измерения вычисляем апостериорные оценки:
G[k] = P1[k] / ( P1[k] + R )
xest2[k] = xest1[k] + G[k] * ( y[k] — xest1[k] )
P2[k] = (1 — G[k]) * P1[k]
plt.title('Ошибки при подавлении шумов \n с %s'%nr, size=12)
valid_iter = arange(1, n_iter,1) # P1 на 0 м шаге не определено
plt.plot(valid_iter, P1[valid_iter])
plt.xlabel('Номер итерации')
plt.ylabel('Априорная оценка ошибки')
plt.setp(plt.gca(), 'ylim', [0, .01] )
plt.show()

0
А если отложить модуль ошибки пунктиром на каждой итерации и сравнить с оценкой ошибки?
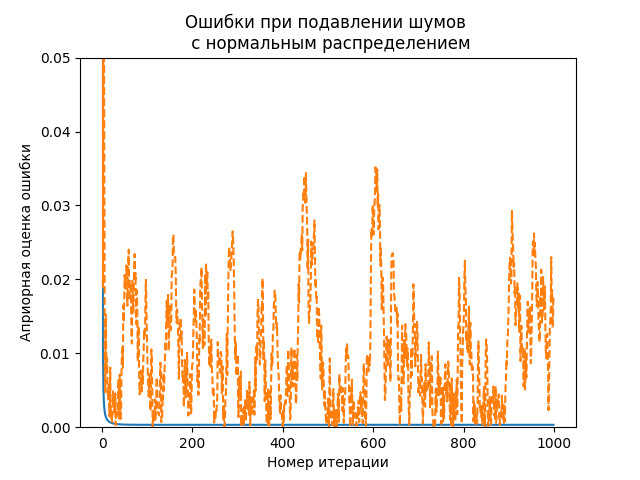
Вас не смущает оценка ошибки и сама ошибка?

Вас не смущает оценка ошибки и сама ошибка?
code.py
from numpy import *
import matplotlib.pyplot as plt
from scipy.stats import norm
n_iter = 1000 # Число итераций.
sz = (n_iter,) # Размер массива
x =2 # Истинное значение измеряемой величины (фильтру неизвестно)
R1 = 0.1 # Ср. кв. ошибка измерения.
R = R1*R1 # Дисперсия
nr="нормальным распределением"
y=norm.rvs( x, R1, size=sz)
Q = 1e-5 # Дисперсия случайной величины в модели системы
xest1 = zeros(sz) # Априорная оценка состояния
xest2 = zeros(sz) # Апостериорная оценка состояния
P1 = zeros(sz) # Априорная оценка ошибки
P2 = zeros(sz) # Апостериорная оценка ошибки
G = zeros(sz) # Коэффициент усиления фильтра
err1=zeros(sz) # Ошибка оценки состояния
xest2[0] = 0.0
P2[0] = 1.0
for k in arange(1, n_iter,1): # Цикл по отсчётам времени.
xest1[k] = xest2[k-1] # Априорная оценка состояния.
P1[k] = P2[k-1] + Q # Априорная оценка ошибки.
# После получения нового значения измерения вычисляем апостериорные оценки:
G[k] = P1[k] / ( P1[k] + R )
xest2[k] = xest1[k] + G[k] * ( y[k] - xest1[k] )
P2[k] = (1 - G[k]) * P1[k]
err1[k]=abs(xest1[k]-x)
plt.title('Ошибки при подавлении шумов \n с %s'%nr, size=12)
i = arange(1, n_iter,1) # P1 на 0 м шаге не определено
plt.plot(i, P1[i])
plt.plot(i, err1[i],'--')
plt.xlabel('Номер итерации')
plt.ylabel('Априорная оценка ошибки')
plt.setp(plt.gca(), 'ylim', [0, 0.05] )
plt.show()
0
Фильтр имеет свой алгоритм работы. То что Вы сделали отношения к ошибке не имеет а свидетельствует только о неизменности дисперсии шума !!!..
0
О терминологии- Оценка погрешности численного интегрирования. Различают два вида оценок априорные и апостериорные. Априорную оценку получают заранее, до проведения расчетов, на основе теоретического анализа квадратурной формулы. Апостериорную оценку определяют после вычислений на основе сопоставления результатов расчетов, проведенных при разных числах отрезков разбиения
0
А причем тут численное интегрирование. Априорную оценку мы знаем т.к. сами задали распределение случайной величины. А апостериорную можно определить оценив результат с полученный с разной степенью точности. Для численного интегрирования есть простой метод оценки — процесс Эйткена.
Но какое отношение это имеет к вашим измерениям?
Вы измеряете конкретную физическую величину (которая постоянна за время наблюдения, но имеет неустранимый шум) при этом вы оцениваете не ошибку того что измеряете, а ошибку каких-то внутренних параметров какого-то вспомогательного фильтра. Более того вводите еще и энтропийную погрешность. Нафига?
Но какое отношение это имеет к вашим измерениям?
Вы измеряете конкретную физическую величину (которая постоянна за время наблюдения, но имеет неустранимый шум) при этом вы оцениваете не ошибку того что измеряете, а ошибку каких-то внутренних параметров какого-то вспомогательного фильтра. Более того вводите еще и энтропийную погрешность. Нафига?
-1
Sign up to leave a comment.
Articles
Change theme settings
Фильтр Калмана для минимизации энтропийного значения случайной погрешности с не Гауссовым распределением