
В 1974 году британский математик Роджер Пенроуз создал революционный набор плиток, который можно использовать для заполнения бесконечной плоскости никогда не повторяющимся узором. В 1982 году израильский кристаллограф Даниэль Шехтман открыл металлический сплав, атомы которого были выстроены в порядке, никогда ранее не встречавшемся в материаловедении. Пенроуз достиг масштабного общественного признания, редко достающегося математикам. Шехтман получил Нобелевскую премию. Оба учёных бросили вызов человеческой интуиции и изменили основы понимания структуры природы, обнаружив, что бесконечная вариативность может возникать даже в высокоупорядоченной среде.
В фундаменте их открытий лежит «запрещённая симметрия», названная так, потому что она противоречит глубоко укоренившейся связи между симметрией и повторяемостью. Симметрия основана на осях отражения — всё, что есть с одной стороны линии, дублируется и на другую. В математике эта связь выражена паттернами замощения пространства. Симметричные формы, например, прямоугольники и треугольники, могут заполнять плоскость без пропусков и наложений, создавая постоянно повторяющийся узор. Повторяющиеся узоры называются «периодическими» и про них говорят, что они имеют «симметрию переноса». Если перемещать узор (паттерн) с места на место, он будет выглядеть одинаково.
Будучи смелым и амбициозным учёным, Пенроуз больше интересовался не одинаковыми паттернами и повторяемостью, а бесконечной вариативностью. Конкретнее, его интересовало «апериодическое» замощение, то есть наборы фигур, которые могут заполнять бесконечную плоскость без пропусков и наложений, а паттерн замощения при этом никогда не повторяется. Это была трудная задача, потому что он не мог использовать фигуры (плитки) с двумя, тремя, четырьмя или шестью осями симметрии — прямоугольники, треугольники, квадраты или шестиугольники — потому что на бесконечной плоскости они будут создавать периодические или повторяющиеся паттерны. То есть ему нужно было использовать фигуры, которые, как считалось, оставляют пропуски при заполнении плоскости — фигуры, имеющие запрещённую симметрию.
Для создания своей плоскости неповторяющихся паттернов Пенроуз обратился к пятиосевой симметрии — к пятиугольниуку, в частности потому, что, по его словам, на пятиугольники «просто приятно смотреть». Примечательным в фигурах Пенроуза было то, что хотя он получил эти фигуры из линий и углов прямоугольников, они не оставляли некрасивых пропусков. Они плотно прилегали друг к другу, изгибаясь и поворачиваясь на плоскости, всегда находясь близко к повторяемости, но никогда не достигая её.
Мозаика Пенроуза захватила внимание общественности по двум основным причинам. Во-первых, он нашёл способ генерации бесконечно меняющихся узоров всего из двух типов фигур. Во-вторых, его плитки были простыми, симметричными фигурами, которые сами по себе не выказывали никаких признаков необычных свойств.

Пенроуз создал несколько разновидностей своих апериодических наборов фигур. Одна из самых известных называется «змей» и «дротик». «Змей» выглядит как детский воздушный змей, а «дротик» — как упрощённый контур стелс-бомбардировщика. Оба чётко делятся по осям симметрии и каждый из них имеет на поверхности простые симметричные дуги. Пенроуз определил одно правило размещения фигур: для «правильного» размещения плиток эти дуги должны совпадать, создавая неразрывные кривые. Без этого правила «змеев» и «дротики» можно располагать в повторяющихся паттернах. Если соблюдать это правило, то повторения не возникают никогда. «Змей» и «дротик» бесконечно заполняют плоскость, танцуя вокруг своих пяти осей, создавая звёзды и десятиугольники, изгибающиеся кривые, бабочек и цветы. Фигуры повторяются, но в них появляются новые вариации.
Клинический профессор математики Эдмунд Харрисс из Университета Арканзаса, написавший докторскую о плитках Пенроуза, предлагает такое сравнение. «Представьте, что вы живёте в мире, состоящем из квадратов. Вы начинаете идти, и когда добираетесь до конца квадрата, следующий оказывается точно таким же, и вы знаете, что будете видеть, если продолжите двигаться бесконечно». Плитки Пенроуза имеют ровно противоположную природу. «Какой бы информацией вы ни обладали, какую бы часть паттерна ни видели, вы никогда не сможете предугадать, что встретится следующим. Всегда найдётся что-то, чего вы не видели раньше».
Один из любопытных аспектов апериодического разбиения плоскости заключается в том, что информация о позиционировании каким-то образом передаётся на большие расстояния — плитка Пенроуза, положенная в одном месте, мешает размещению других плиток в сотнях (а также тысячах и миллионах) плиток от неё. «Локальное ограничение каким-то образом создаёт глобальное ограничение», — говорит Харрисс. «Это предполагает, что ни в каких масштабах эти плитки не создадут чего-то периодического». Перед вами может встать выбор поместить, допустим, «змея» в одной области, или «дротик» в каком-то отдалённом месте. Подойдёт любая из плиток, но не обе.
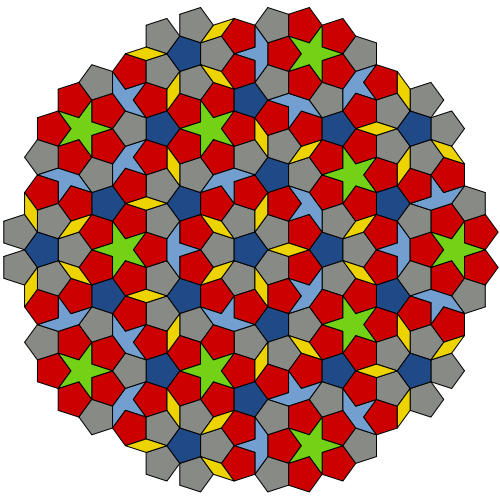
Эти плитки, формирующие бесконечный неповторяющийся паттерн, выражают пропорцию Фибоначчи, также известную как «золотое сечение». Говорят, что два числа имеют золотое сечение, если отношение меньшего числа к большему такое же, что отношение большего числа к сумме двух чисел. В данном случае отношение площади «змея» к площади «дротика» составляет золотое сечение. Отношение длинной стороны «змея» к его короткой стороне тоже является золотым сечением.
Плитки Пенроуза также можно подразделить на меньшие версии самих себя. «Змей» состоит из двух «змеев» поменьше и из двух половинок «дротика». «Дротик» состоит из уменьшенного «змея» и двух половик «дротика». (В любом правильном замощении Пенроуза эти половины «дротиков» выравниваются друг относительно друга. С точки зрения математики это позволяет их считать целыми «дротиками».) «Допустим, у нас есть кусок мозаики Пенроуза, состоящий из A „змеев“ и B „дротиков“», — говорит Харрисс. «Если я их подразделю, то получу 2A+B „змеев“, и A+B „дротиков“».
Если проделать такую подстановку бесконечное количество раз, то можно подсчитать общую долю каждого типа плиток, как бы выложенных на бесконечной плоскости. В таких вычислениях повторяющийся паттерн всегда приводит к рациональному числу. Если доля является иррациональным числом, то это означает, что паттерн никогда на самом деле полностью не повторится. При вычислениях для плиток Пенроуза не только получается иррациональное число, их соотношение является пропорцией Фибоначчи — отношение «дротиков» к «змеям» равно отношению «змеев» к общему количеству плиток.
Учитывая то, что пропорция Фибоначчи повсеместно встречается в природе — от ананасов до популяций кроликов — ещё более странно, что эта пропорция является фундаментальной для системы замощения, которая, казалось бы, не имеет ничего общего с физическим миром. Пенроуз создал нечто новое в науке, интригующее именно там, что оно не должно работать так, как это делает природа. Это походило на то, как будто Пенроуз написал фантастический рассказ о новом виде животных, а потом зоолог обнаружил этот вид живущим на Земле. На самом деле, плитки Пенроуза связаны с золотым сечением, с изобретённой нами математикой, и математикой окружающего нас мира.

Взявшись за изучение запрещённой симметрии, Пенроуз не мог догадываться, что он стал частью сдвига мышления, который привёл к открытию новой области математической науки. В конце концов, симметрия фундаментальна и для чистой математики, и для мира природы. Астрофизик Марио Ливио назвал симметрию «одним из самых необходимых инструментв для расшифровки структуры природы». Природа использует квадраты и шестиугольники по той же причине, что и люди: они просты, эффективны и упорядочены. Если уж пятиугольники казались непрактичными даже для столь простой задачи, как заполнение плиткой пола в дизайне интерьеров, то, разумеется, считалось, что их невозможно использовать для создания атомов в твёрдых материалах наподобие кристаллов.
Кристаллы состоят из трёхмерных решёток атомов. Кристаллы растут, добавляя новые атомы и расширяя решётки. Это происходит наиболее эффективно, когда атомы выстраиваются в повторяющиеся паттерны. В течение десятилетий история на этом заканчивалась: кристаллы были повторяющимися структурами. Точка.
Но затем, в 1982 году, Шехтман ушёл в творческий отпуск из Университета Технион в Хайфе и начал работать в Национальном бюро стандартов. Он возился в лаборатории с алюминиево-марганцевым сплавом. Дифракционные картины, создаваемые его кристаллическими структурами, казалось, не походили ни на одну из стандартных симметрий, известных кристаллографам. На самом деле, атомы выстраивались в те самые пятиугольники, ромбы, «змеи» и «дротики», которые Пенроуз открыл в мире математики.
«Разумеется, я был знаком с плитками Пенроуза», — рассказывает Шехтман. Но он не имел никаких причин подозревать их связь с этим сплавом. «Я не понимал, что это такое. В течение следующих месяцев я снова и снова повторял свои эксперименты. К концу творческого отпуска я точно знал, чем это не является, но по-прежнему понятия не имел, что же это».
Чтобы понять, что он обнаружил, Шехтману, как и Пенроузу, пришлось подвергнуть сомнению привычные интуитивные представления. Ему пришлось принять запрещённую симметрию и её пятиугольную неразбериху с отсутствием повторяемости. Находясь в Израиле, он неохотно пришёл к признанию того, что обнаружил неповторяющуюся кристаллическую атомную структуру. Однако никто из мира материаловедения не мог поначалу отнести это открытие к кристаллам. Поэтому их назвали «квазикристаллами».
Причудливая математика Пенроуза как будто прорвалась наружу, в мир природы. «В течение 80 лет кристаллы определяли как „упорядоченные и периодические“ структуры, потому что все кристаллы, которые мы изучали с 1912 года, были периодическими», — объясняет Шехтман. «И только в 1992 году Международный союз кристаллографов организовал комитет для подбора нового определения слову „кристалл“. Это новое определение стало сдвигом парадигмы для кристаллографии».
Понять и принять открытие Шехтмана мешала не только простая инерция мышления. Апериодические кристаллические структуры были не просто незнакомыми — они считались неестественными. Вспомним, что расположение одной плитки Пенроуза может влиять на фигуры в тысячах плиток от неё — локальные ограничения создают глобальные. Но если кристалл формируется атом за атомом, то не должно существовать закона природы, создающего ограничения, свойственные плиткам Пенроуза.
Оказалось, что кристаллы не всегда формируются атом за атомом. «В очень сложных интерметаллических соединениях элементы огромны. Они не локальны», — рассказывает Шехтман. Когда большие фрагменты кристалла формируются одновременно, а не постепенным разрастанием атомов, расположенные очень далеко друг от друга атомы могут влиять на взаимное положение, в точности, как в плитках Пенроуза.
Как это бывает со многими табу, запрещённая симметрия получила признание как одна из допустимых форм существования в природе. Квазикристаллы не только стали объектом изучения новой области научных исследований: оказалось, что у них имеется множество полезных свойств, возникающих вследствие их необычной структуры. Например, их несимметричная конфигурация атомов обеспечивает им низкую поверхностную энергию, то есть к ним немногое может прилипнуть. Таким образом квазикристаллические покрытия начали использоваться в антипригарной кухонной утвари. (Когда Пенроуз создавал свои новые плитки, он и представить не мог, что они будут использоваться в кристаллографии, не говоря уж о жарке яиц.) Кроме того, квазикристаллы обычно обладают низким трением и износом, поэтому они являются идеальными покрытиями для бритвенных станков и хирургических инструментов, или любых других острых инструментов, касающихся тела человека.

Так как структуры квазикристаллов никогда не повторяются, они создают уникальные дифракционные картины электромагнитного излучения. Исследователей в области фотоники интересует, как они влияют на светопропускание, отражаемость и фотолюминесценцию. Если их охладить, то их электрическое сопротивление падает до почти нулевого уровня. Но также они поглощают инфракрасное излучение, благодаря чему очень быстро нагреваются до высоких температур. Благодаря этому они оказываются очень полезным дополнением к 3D-принтерам, в которых в качестве исходного материала используется пластиковый порошок. Шехтман объясняет: если примешать к нему квазипероиодический порошок и подвергнуть воздействию инфракрасного излучения, то квазипериодический порошок «чрезвычайно быстро нагревается и расплавляет окружающие его частицы пластика, из-за чего они склеиваются».
Никто не знает, как закончится история запрещённой симметрии. Математики продолжают исследовать свойства плиток Пенроуза. Квазикристаллы остаются объектом изучения и фундаментальных, и прикладных исследований. Но пока это путешествие было невероятным. За последние 40 лет пятиосевая симметрия превратилась из непрактичной в ценную, из неестественной в совершенно естественную, из запрещённой в господствующую. И за это превращение мы должны поблагодарить двух учёных, отказавшихся от привычных представлений, чтобы открыть примечательную новую форму бесконечных вариаций в природе.
Об авторе: Пэтчен Барс — журналист и автор из Торонто. В настоящее время он работает над книгой о взаимосвязи между чистой математикой и миром природы.