Под катом исследуется вопрос, как должен быть устроен хороший алгоритм многомерной индексации. На удивление, вариантов не так уж и много.
Одномерные индексы, B-деревья
Мерилом успеха поискового алгоритма будем считать 2 факта —
- установление факта его наличия или отсутствия результата происходит за логарифмическое (по отношению к размеру индекса) число чтений дисковых страниц
- стоимость выдачи результата пропорциональна его объему
В этом смысле B-деревья вполне успешны и причиной этого можно считать использование сбалансированного дерева. Простота алгоритма обусловлена одномерностью пространства ключа — при необходимости расщепить страницу, достаточно разделить надвое отсортированное множество элементов этой страницы. В общем случае делят по числу элементов, хотя это необязательно.
Т.к. страницы дерева хранятся на диске, можно сказать, что B-дерево имеет возможность очень эффективно преобразовывать одномерное пространство ключа в одномерное же дисковое пространство.
При заполнении дерева более-менее “правой вставкой”, а это довольно распространённый случай, страницы порождаются в порядке роста ключа, время от времени перемежаясь вышестоящими страницами. Есть неплохие шансы, что и на диске они окажутся рядом. Таким образом без всяких усилий достигается высокая локальность данных — близкие по значению данные окажутся где-то рядом и на диске.
Конечно, при вставке значений в произвольном порядке ключа и страницы порождаются произвольным образом, в результате чего растёт т.н. фрагментация индекса. Есть и средства борьбы с фрагментацией, которые восстанавливают локальность данных.
Казалось бы, в наш век RAID и SSD дисков порядок чтения с диска не имеет значения. Но, скорее, он не имеет такого значения, как раньше. В SSD диске нет физического проброса головок, поэтому его скорость при случайном чтении в сравнении с чтением сплошным не падает сотни раз, как у HDD. А только лишь раз в 10 и более.
Вспомним, что появились B-деревья в 1970 г. в эпоху магнитных лент и барабанов. Когда различие в скорости произвольного доступа для упомянутых ленты и барабана было куда как более драматичным, нежели в сравнении HDD и SSD.
Кроме того, 10 раз тоже имеют значение. И в эти 10 раз входит не только физические особенности SSD, но и принципиальный момент — предсказуемость поведения читателя. Если читатель с большой вероятностью за данным блоком попросит следующий, есть смысл загрузить его превентивно, по предположению. А если поведение хаотично, все попытки предсказания бессмысленны и даже вредны.
Многомерное индексирование
Далее будем иметь дело с индексом двумерных точек (X,Y), просто потому, что с ними удобно и наглядно работать. А проблемы принципиально те же.
Простой, “бесхитростный” вариант с отдельными индексами по X и Y не проходит по нашему критерию успешности. Он не даёт логарифмической стоимости получения первой точки. В самом деле, чтобы ответить на вопрос, а есть ли вообще что-то в искомом экстенте, мы должны
- сделать поиск в индексе X и достать все идентификаторы из X-интервала экстента
- аналогично для Y
- пересечь эти два множества идентификаторов
Уже первый пункт зависит от размера экстента и не гарантирует логарифма.
Чтобы быть “успешным”, многомерный индекс должен быть устроен как более-менее сбалансированное дерево. Это утверждение может показаться спорным. Но требование логарифмического поиска диктует нам именно такое устройство. Почему не два дерева или не больше? Уже рассматривали “бесхитростный” и непригодный вариант с двумя деревьями. Возможно, существуют и пригодные. Но два дерева — это в два раза больше (в том числе одновременных) блокировок, в два раза выше стоимость, существенно большие шансы поймать дедлок. Если есть возможность обойтись одним деревом, непременно надо ей воспользоваться.
Учитывая всё это, вполне закономерно желание взять за основу очень удачный опыт B-дерева и “обобщить” его для работы с двумерными данными.
Так появилось R-дерево.
R-дерево
R-дерево устроено следующим образом:
Изначально у нас пустая страница, просто добавляем в нее данные (точки).
Но вот страница переполнилась и её надо расщеплять.
В B-дереве элементы страницы упорядочены естественным образом, так что вопрос лишь сколько резать. В R-дереве естественного порядка нет. Варианта два:
- Привнести порядок, т.е. ввести функцию, которая на основании X&Y выдаст значение, по которому элементы страницы будут упорядочены и в соответствии с ним же разделены. В этом случае весь индекс выродится в обычное B-дерево, построенное по значениям указанной функции. Кроме очевидных плюсов есть и большой вопрос — ну хорошо, мы проиндексировали, а как искать? Об этом позже, сначала рассмотрим второй вариант.
- Разделить страницу по пространственному критерию. Для этого каждой странице должен быть приписан экстент расположенных на/под ней элементов. Т.е. корневая страница имеет экстент всего слоя. При расщеплении порождаются две (или более) страницы, экстенты которых включены в экстент родительской страницы (для поиска).
Здесь сплошная неопределённость. Как именно расщеплять страницу? По горизонтали или вертикали? Исходить из половины площади или половины элементов? А что, если точки образовали два кластера, но разделить их можно только линией наискосок? А если кластеров три?
Само наличие подобных вопросов указывает, что R-дерево не является алгоритмом. Это набор эвристик, как минимум — для расщепления страницы при вставке, для слияния страниц при удалении/модификации, для препроцессинга при массовой вставке.
Эвристика предполагает специализацию конкретного дерева на определенном типе данных. Т.е. на датасетах определенного вида она ошибается реже. “Совсем не ошибаться эвристика не может, т.к. в этом случае она была бы алгоритмом”©.
Что означает в данном контексте ошибка эвристики? Например, что страница будет расщеплена/слита неудачно и страницы начнут частично перекрывать друг друга. Если вдруг поисковый экстент придётся на область перекрытия страниц, стоимость поиска уже будет не совсем логарифмической. Со временем по мере вставок/удалений количество ошибок накапливается и производительность дерева начинает деградировать.
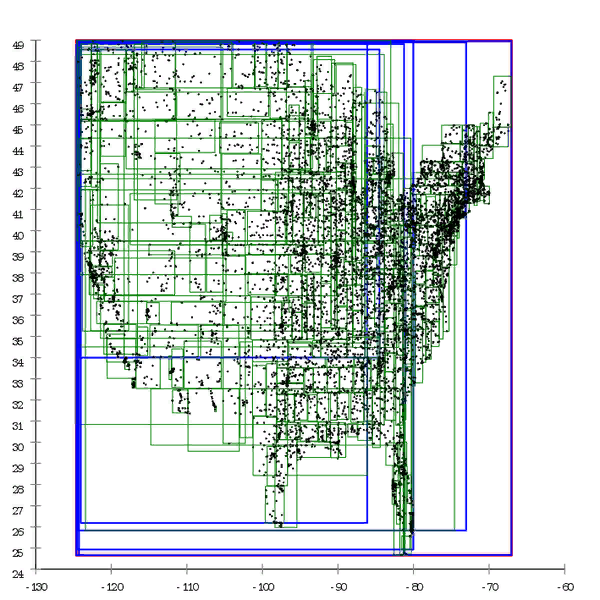
Фиг.1 Вот пример R*-дерева, которое построено естественным путём
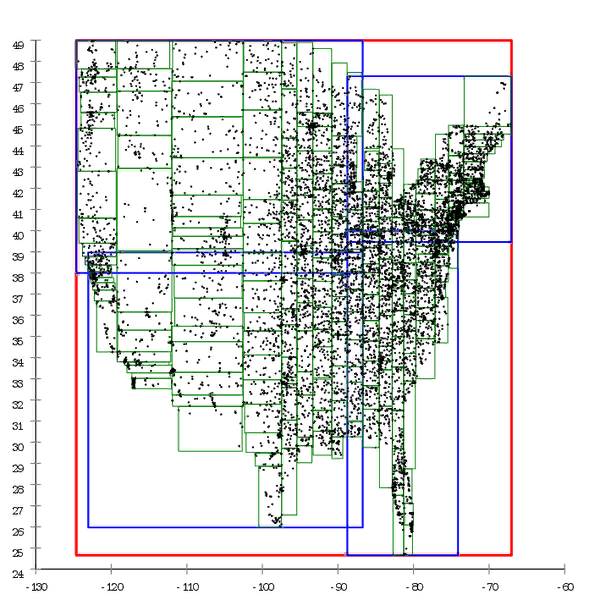
Фиг.2 А здесь тот же датасет предобработан и дерево построено массовой вставкой
Можно сказать, что B-дерево тоже со временем деградирует, но это немного другая деградация. Производительность B-дерева падает от того, что его страницы идут не подряд. Это легко лечится “выпрямлением” дерева — дефрагментацией. В случае R-дерева так легко не отделаться, сама структура дерева “кривая”, чтобы исправить ситуацию, его требуется полностью перестроить.
Обобщения R-дерева на многомерные пространства неочевидны. Допустим при расщеплении страниц мы минимизировали периметр дочерних страниц. Что минимизировать в трёхмерном случае? Объем или площадь поверхности? А в восьмимерном случае? Здравый смысл здесь уже не советчик.
Индексируемое пространство вполне может быть не изотропным. Почему бы не проиндексировать не просто точки, а их позиции во времени, т.е. (X,Y,t). В этом случае, например, эвристика, опирающаяся на периметр бессмысленна т.к. складывает длину с интервалами времени.
Общее впечатление от R-дерева — это что-то вроде жаброногих рачков. Те имеют свою экологическую нишу, в которой соревноваться с ними трудно. Но в общем случае не имеют шансов при конкуренции с более развитыми животными.
Квадродерево
В квадродереве каждая нелистовая страница имеет ровно четырёх потомков, которые поровну делят её пространство на квадранты.

Фиг.3 Пример построенного квадродерева
Это не самая удачная конструкция с точки зрения баз данных.
- Каждая страница сужает пространство поиска по каждой из координат только в два раза. Да, это обеспечивает логарифмическую сложность поиска, но это логарифм по основанию 2, а не число элементов на странице, (пусть 100) как в B-дереве.
- Каждая страница мала, но за ней всё равно приходится лезть на диск.
- Глубину квадродерева приходится ограничивать, иначе его несбалансированность сказывается на производительности. В результате на сильно кластеризованных данных (например, дома на карте — в городах их много, в полях — мало) на листовых страницах может скапливаться большое количество данных. Индекс из точного становится блочным и требует постобработки.
Неудачно выбранный размер решетки (глубина дерева) может убить производительность. Хочется всё же, чтобы работоспособность алгоритма не зависела критически от человеческого фактора.
- Затраты пространства на хранение одной точки довольно велики.
Нумерация пространства
Осталось рассмотреть отложенный ранее вариант с функцией, которая на основании многомерного ключа вычисляет значение для записи в обычном B-дереве.
Построение такого индекса очевидно, а сам индекс обладает всеми плюсами B-дерева. Вопрос лишь в том, можно ли этот индекс использовать для эффективного поиска.
Существует огромное к-во таких функций, можно предположить, что среди них есть небольшое количество “хороших”, большое количество “плохих” и огромное количество “просто ужасных”.
Найти ужасную функцию несложно — сериализуем ключ в строку, считаем от неё MD5 и получаем совершенно бесполезное для наших целей значение.
А как подступиться к хорошим? Уже говорилось, полезный индекс обеспечивает “локальность” данных — близкие в пространстве точки и при сохранении на диск часто оказываются недалеко друг от друга. В применении к искомой функции это означает, что для пространственно близких точек она даёт близкие значения.
Попав в индекс, вычисленные значения окажутся на «физических» страницах в порядке своих значений. С точки “физического смысла”, поисковый экстент должен затрагивать по возможности меньшее количество физических страниц индекса. Что в общем то очевидно. С этой точки зрения, нумерующие кривые, которые “вытягивают” данные — “плохие”. А те, что “запутывают в клубок” — ближе к ”хорошим”.
Наивная нумерация
Попытка втиснуть отрезок в квадрат (гиперкуб) оставаясь в логике одномерного пространства т.е. порезать на куски и заполнить квадрат этими кусками. Это может быть
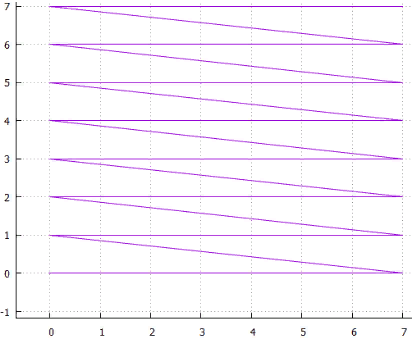
Фиг.4 строчная развёртка
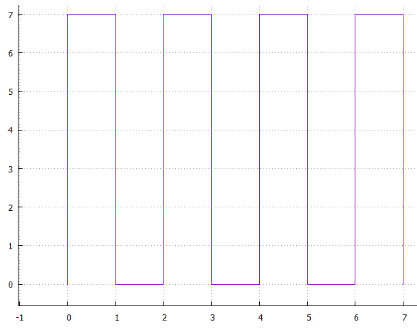
Фиг.5 чересстрочная развёртка
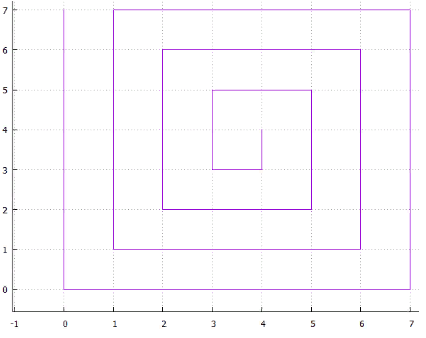
Фиг.6 спираль
или … можно придумать очень много вариантов, всем им присущи два недостатка
- неоднозначность, например: а почему спираль завита по часовой стрелке а не против или почему строчная развёртка сначала по X а потом по Y
- наличие протяженных прямых кусков, которые делают использование подобного метода малоэффективным в целях многомерного индексирования (большой периметр страниц)
Функции прямого доступа
Если основная претензия к “наивным” методам в том, что они порождают сильно вытянутые страницы, давайте порождать “правильные” страницы самостоятельно.
Идея проста — пусть есть внешнее разбиение пространства на блоки, присвоим каждому блоку идентификатор и это будет ключ пространственного индекса.
- пусть координаты X&Y 16-разрядные (для наглядности)
- мы собираемся покрыть пространство квадратными блоками размером 1024X1024
- загрубляем координаты, сдвигаем на 10 разрядов вправо
- и получаем идентификатор страницы, склеиваем разряды от X&Y. Теперь в идентификаторе младшие 6 разрядов — старшие от X, следующие 6 разрядов — старшие от Y
Нетрудно увидеть, что блоки образуют строчную развёртку, поэтому для нахождения данных для поискового экстента придётся сделать поиск/чтение в индексе для каждой строки блоков, на которые лёг этот экстент. В целом, этот метод отлично работает, хотя и обладает рядом недостатков.
- при создании индекса придётся выбрать оптимальный размер блока, который совершенно неочевиден
- если блок существенно больше типичного запроса, поиск будет неэффективным т.к. придется прочитать и отфильтровать (постпроцессинг) слишком много
- если блок существенно меньше типичного запроса, поиск будет неэффективным т.к. придётся делать много запросов по строкам
- если на блоке в среднем слишком много или мало данных, поиск будет неэффективным
- если данные кластеризованы (ex: дома на карте), поиск будет не везде эффективен
- если датасет вырос, вполне может оказаться, что размер блока перестал быть оптимальным.
Частично эти проблемы решаются путём построения многоуровневых блоков. Для того же примера:
- по прежнему желаем блоки размером 1024X1024
- но теперь у нас еще будут блоки высшего уровня размером 8X8 низших блоков
- ключ устроен так (от младших к старшим разрядам):
3 разряда — разряды 10...12 X координаты
3 разряда — разряды 10...12 Y координаты
3 разряда — разряды 13...15 X координаты
3 разряда — разряды 13...15 Y координаты
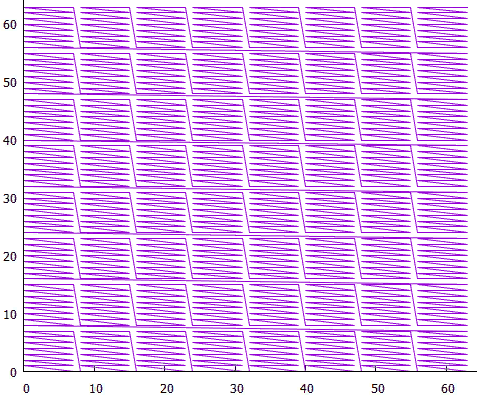
Фиг.7 Блоки низкого уровня образуют блоки высокого уровня
Теперь для больших экстентов не нужно читать огромное к-во маленьких блоков, это делается за счет блоков высокого уровня.
Интересно, что можно было не загрублять координаты, а в той же манере втиснуть их в ключ. В этом случае постфильтрация обошлась бы дешевле т.к. происходила бы при чтении индекса.
Подобным образом устроены пространственные GRID-индексы в MS SQL, в них допускается до 4 уровней блоков.
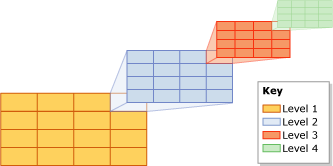
Фиг.8 GRID-индекс
Еще один интересный способ прямой индексации — использование квадродерева для внешнего разбиения пространства.
Квадродерево полезно тем, что умеет подстраиваться к плотности объектов т.к. при переполнении узла он расщепляется. В результате, там где плотность объектов высока, блоки получатся мелкими и наоборот. Это позволяет уменьшить число порожних обращений к индексу.
Правда, квадродерево — конструкция неудобная для перестроения на-лету, выгодно делать это время от времени.
Из приятного, при перестроении квадродерева нет необходимости перестраивать индекс, если блоки идентифицируются по коду Мортона и объекты закодированы с его же помощью. Здесь фокус вот в чем — если координаты точки закодированы кодом Мортона, идентификатор страницы является префиксом в этом коде. При поиске данных страницы, выбираются все ключи, которые находятся в интервале от [prefix]00...00B до [prefix]11...11B, если страница расщепилась, значит всего лишь префикс её потомков удлинился.
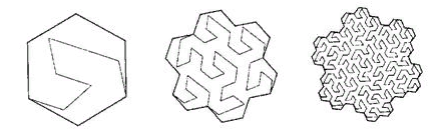
Самоподобные функции
Первое что приходит на ум при упоминании самоподобных функций — “заметающие кривые”. «Заметающая кривая — это непрерывное отображение, областью определения которого служит единичный отрезок [0, 1], а область значений — евклидово (более строго — топологическое) пространство». Примером может служить кривая Пеано
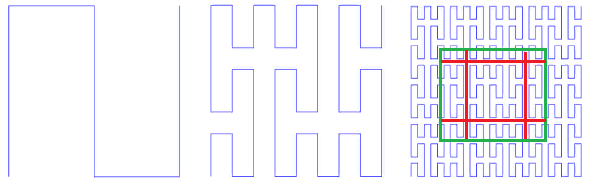
Фиг.9 первые итерации кривой Пеано
В левом нижнем углу находится начало области определения (и нулевое значение функции), в правом верхнем углу конец (и 1), каждый раз, когда мы двигаемся на 1 шаг, добавляем 1/(N*N) к значению (при условии, что N — степень 3, конечно). В результате в верхнем правом углу значение достигает 1. Если же на каждом шаге прибавлять единицу, такая функция просто последовательно пронумерует квадратную решетку, чего мы и хотели.
Все заметающие кривые обладают самоподобием. В данном случае, симплексом является квадрат 3x3, При каждой итерации каждая точка симплекса превращается в такой же симплекс, чтобы обеспечить непрерывность, приходится прибегать к отображениям (переворотам).
Самоподобие — очень важное для нас качество. Оно даёт надежду на логарифмическую стоимость поиска. Например, для симплекса 3х3, все номера, порожденные внутри каждого из 9 элементарных квадратов последующими итерациями детализации будут в пределах одного диапазона. Просто потому, что номер — это путь, пройденный от начала. Т.е. если разделить экстент на 9 частей, содержимое каждой из них может быть получено одним траверзом индекса. И так далее рекурсивно, каждый из 9 под-квадратов каждого из квадратов может быть получен одним запросом к индексу (правда, по меньшему диапазону). А значит поисковый экстент может быть разбит на небольшое число квадратных подзапросов, прочитанных либо целиком либо с фильтрацией (по периметру). На Фиг.9 зеленым показан поисковый экстент, разбитый красными линиями на подзапросы.
Однако, самоподобие не делает автоматически нумерующую кривую пригодной для целей индексирования.
- кривая должна заполнять квадратную решетку. Индексируем мы значения в узлах квадратной решетки и подыскивать каждый раз подходящий узел на решетке, например, треугольной не хочется. Хотя бы для того, чтобы избежать проблем с округлением. Вот, к примеру такая (Фиг.10)

Фиг.10 троичное озеро Коха
кривая нам не подходит. Хотя, она отлично “мостит” поверхность.
- кривая должна заполнять пространство без лакун (фрактальная размерность D=2). Вот это (Фиг.11):
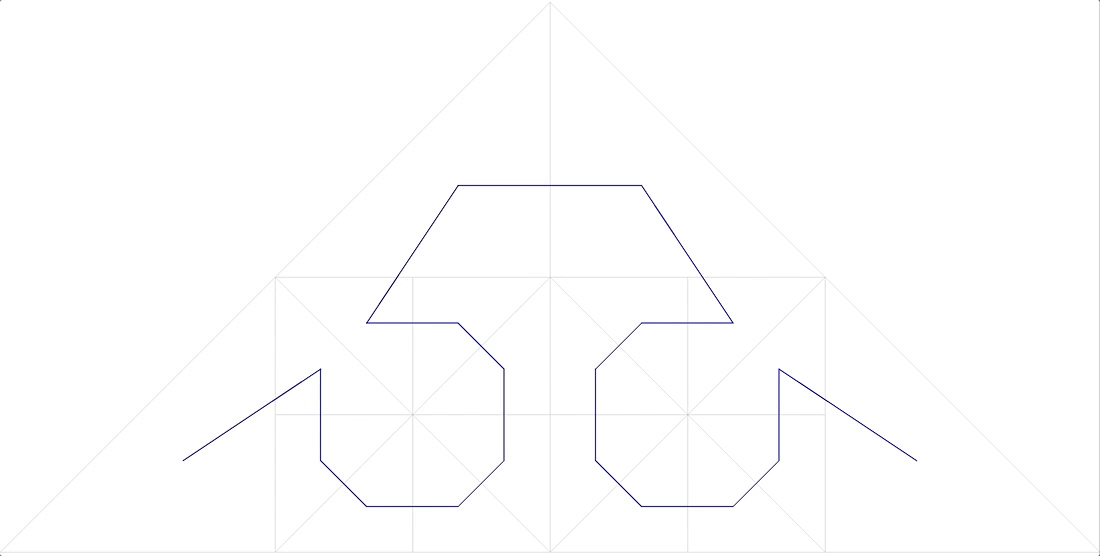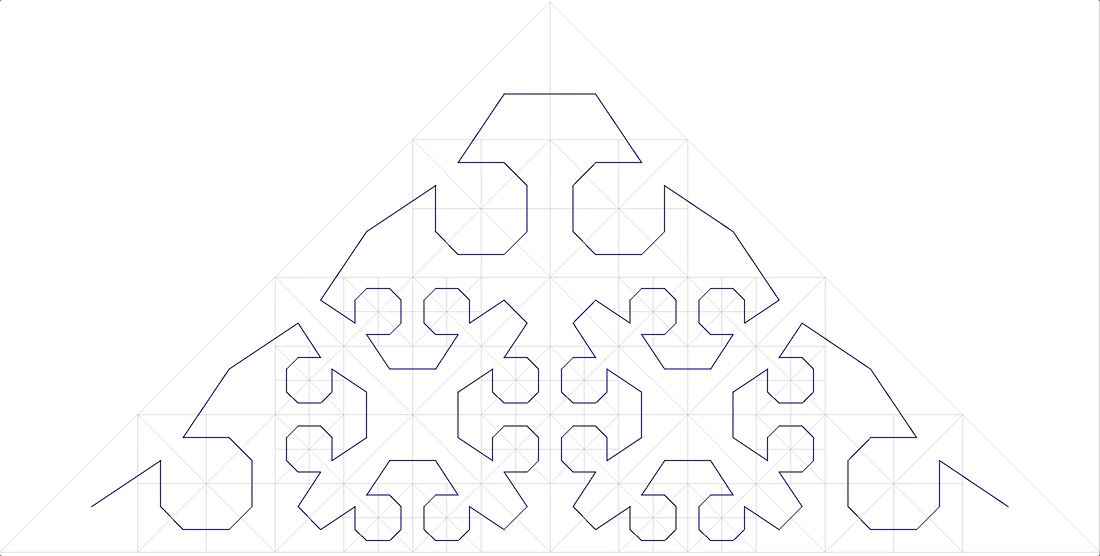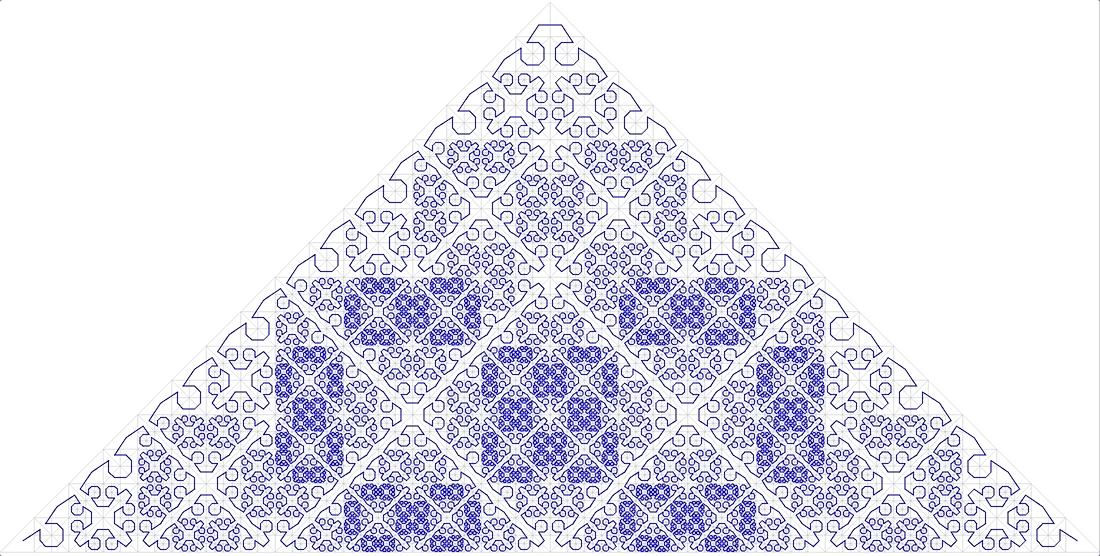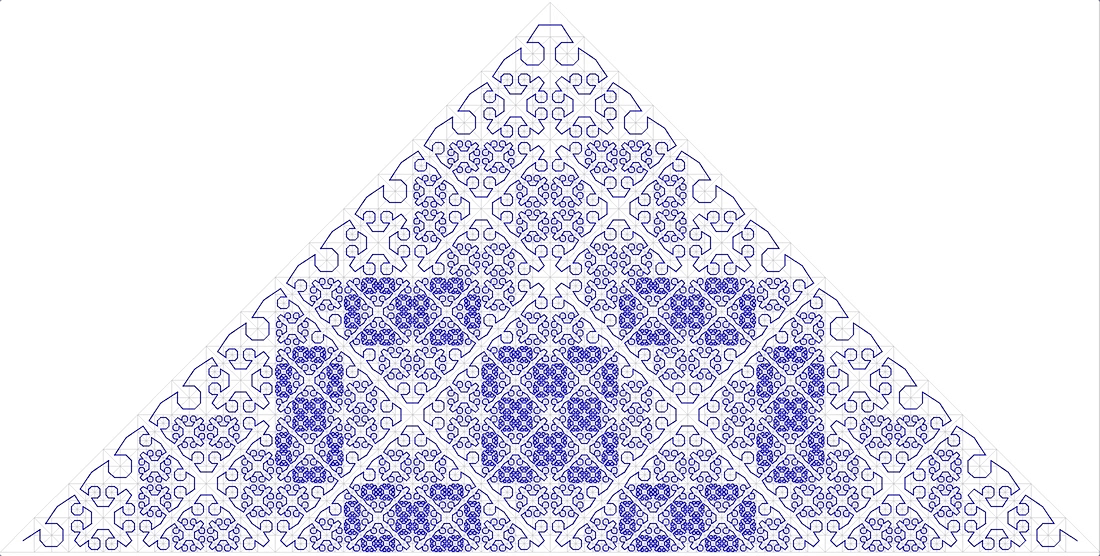
Фиг.11 безымянная фрактальная кривая
тоже не подходит.
- значение нумерующей функции (путь, пройденный по кривой от начала) должно быть легко вычисляемым. Из этого следует, что в силу возникающей неоднозначности не годятся кривые с самокасанием, как кривая Серпинского

Фиг.12 кривая Серпинского
или, что то же самое (для нас), “прохождение треугольника по Чезаро”

Фиг. 13 треугольник Чезаро, для наглядности прямой угол заменен на 85° - в нумерующей функции не должно быть параметров, кривая должна быть единообразной (с точностью до симметрии). Потому как каждый такой параметр делает индекс не универсальным. Пример: комбинация самоподобных кривых с наивным подходом (взято здесь)

Фиг. 14 “A Plane Filling Curve for the Year 2017”
И если направление вращения спирали можно списать на симметрию, то число витков (на максимальном экстенте) и положение центра пришлось бы задать руками.
С точки зрения периметра страниц это, кстати, очень неплохой вариант, но вот стоимость вычисления такой функции вызывает вопросы.
Изотропность — еще одна важная характеристика. Имеется в виду, что функция нумерации должна быть легко обобщаема на более высокие размерности. И хорошо, если для N-мерного куба все его N проекций на размерности (N-1) одинаковы. Это следует из того что, мы используем изотропное пространство и было бы странно, если бы разные оси использовались в функции по-разному.
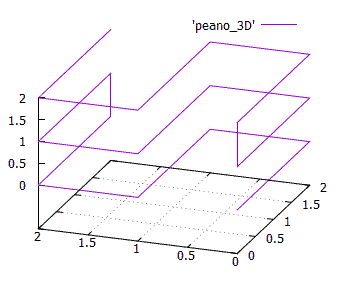
Фиг. 15 Трехмерный симплекс 3x3x3 кривой Пеано
Изотропность не является жестким требованием, но это важный показатель качества нумерующей кривой.
Что касается непрерывности.
Выше мы видели примеры непрерывных нумерующих функций, которые не подходили для наших целей. С другой стороны, вполне разрывная функция строчной развертки с блоками отлично для этого подходит (с некоторыми ограничениями). Мало того, если бы мы построили блочный индекс на основе непрерывной чересстрочной развёртки, с точки зрения производительности это ничего не изменило бы. Потому как если блок вычитывается целиком, нет никакой разницы в каком порядке будут получены объекты.
Для самоподобных кривых это тоже справедливо.
- назовём размером страницы, площадь экстента всех объектов на дисковой странице
- характерным размером будем считать среднюю площадь страницы
- на больших запросах (заметно больше характерного размера) большая часть объектов читается с помощью сплошного чтения больших блоков, а для сплошного чтения порядок и разрывность не важны. Важны они только для периферийных страниц, которые будут прочитаны частично. Но периметр — это в общем случае корень квадратный от числа объектов. И стоимостью его чтения можно пренебречь.
- на маленьких запросах — меньше характерного размера, порядок объектов на странице не имеет значения т.к. её всё равно придётся читать и это и будет основная стоимость поиска.
- стоит беспокоиться только по поводу запросов среднего размера, где периметр занимает значительную часть поискового экстента. Из общих соображений, непрерывная нумерующая кривая расположит данные так, что поисковый экстент будет расположен на меньшем количестве физических страниц. Строго говоря, доказательства этого никто не предоставил, подтверждающие результаты численного эксперимента описаны здесь — использование (непрерывной) кривой Гильберта даёт на 3...10% меньше чтений по сравнению с (разрывной) Z-кривой.
Единицы процентов — это не то, что заставит нас отказаться от изучения разрывных самоподобных кривых.
Симплексы
Из сказанного следует, что для целей многомерной индексации подходят лишь квадратные (гиперкубические) симплексы, рекурсивно применённые нужное (для достаточной детализации решетки) число раз.
Да, есть и другие самоподобные способы замостить квадратную решетку, однако не видно вычислительно-дешевого способа сделать такое преобразование, в том числе и обратное. Возможно, такие числовые выверты существуют, но автору они не известны. Кроме того, квадратные симплексы дают возможность эффективно делить поисковый экстент на подзапросы разрезом по одной из координат. При ломанной границе между симплексами это невозможно.
Почему симплексы именно квадратные, а не прямоугольные? Из соображений изотропности.
Осталось выбрать подходящий размер и нумерацию внутри симплекса (обход).
Чтобы выбрать размер симплекса, необходимо разобраться, на что он влияет. На число порожденных подзапросов, которые придётся создать во время поиска. Например, симплекс 3X3 кривой Пеано разрезается на 3 подзапроса с непрерывными интервалами номеров сначала по X, а затем каждый из них на 3 части по Y. В результате мы вернёмися к следующему этапу рекурсии. Если бы у нас был аналогичный (чересстрочный) симплекс 5X5, его пришлось бы резать на 5 частей. Или на неравные части (ex: 2+3), что странно.
Чем-то это напоминает деревья поиска — можно, конечно использовать и 5-ричные и 7-ричные деревья, на практике же в ходу одни лишь бинарные. Троичные деревья имеют свою узкую нишу для поиска по префиксу. И это не совсем то, что интуитивно понимается под троичными деревьями.
Объясняется это эффективностью. В троичном узле для выбора потомка пришлось бы сделать 2 сравнения. В двоичном дереве этому соответствует выбор среди 4 вариантов. Даже меньшая глубина дерева не перекрывает потерю производительности от возросшего числа сравнений.
Кроме того, если бы 3Х3 было эффективнее чем 2Х2 просто потому, что 3 > 2, 4Х4 было бы эффективнее чем 3Х3, а 8Х8 эффективнее чем 5Х5. Всегда можно найти подходящую степень двойки, которая образуется несколькими итерациями 2Х2…
А на что влияет обход симплекса? В первую очередь на число порождённых при поиске подзапросов. Т.к. это хорошо, если симплекс позволяет разрезать себя на куски с непрерывными интервалами номеров. Вот Пеано 3X3 позволяет, поэтому одна итерация режет его на 3 части. А если взять 8x8 симплекс с обходом шахматным конём (Фиг.16), единственный вариант — сразу на 64 элемента.

Фиг. 16 Один из вариантов обхода симплекса 8x8
Итак, раз мы выяснили, что оптимальным симплексом является 2x2, следует рассмотреть, какие варианты существуют для него.

Фиг. 17 Варианты обхода симплекса 2x2
Их, с точностью до симметрии, всего три, условно назовём как “Z”, “омега” и “альфа”.
Сразу бросается в глаза, что “альфа” пересекает сама себя, а значит непригодна для двоичного расщепления. Её бы пришлось разрезать сразу на 4 части. Или на 256 в 8-мерном случае.
Возможность использовать единый алгоритм для пространств разной размерности, (которой мы лишены в случае кривой типа “альфа”), выглядит очень привлекательно. Поэтому в дальнейшем будем рассматривать только два первых варианта.
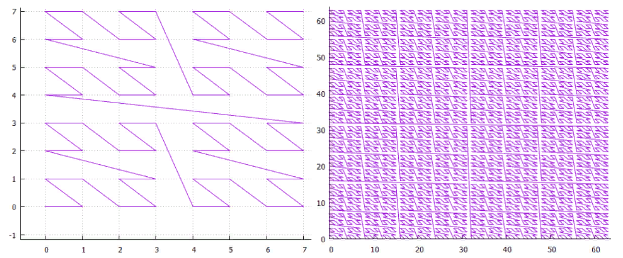
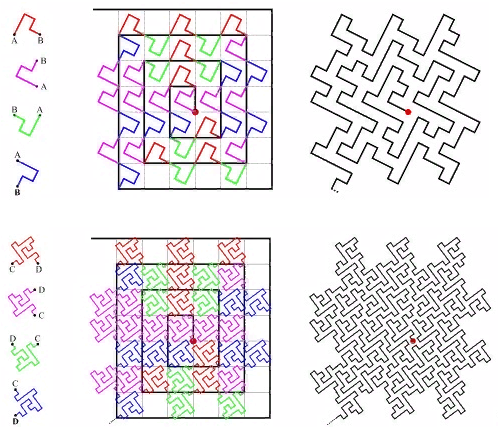
Фиг. 18 Z-кривая
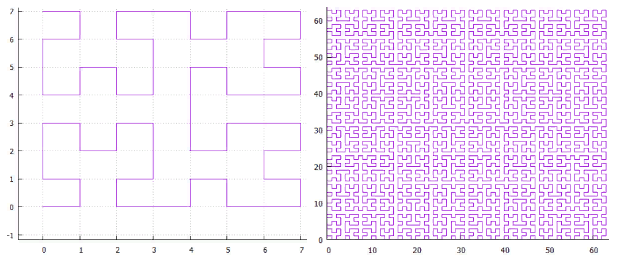
Фиг. 19 “омега” — кривая Гильберта
Раз эти кривые имеют близкую родственную связь, их удаётся обрабатывать одним алгоритмом. Основная специфика кривой локализуется в расщеплении подзапроса.
- сначала найдём стартовый экстент, это минимальный прямоугольник, который включает поисковый экстент и содержит один непрерывный интервал значений ключа.
Находится от следующим образом —
- вычисляем значения ключа для левой нижней и правой верхней точек поискового экстента (KMin, KMax)
- находим общий двоичный префикс (от старших разрядов к младшим) для KMin, KMax
- зануляя все разряды за префиксом, получаем SMin, заполняя их единицами, получаем SMax
- Делаем обратное преобразование ключей в координаты и находим углы стартового экстента. В случае кривой Гильберта, кстати, левый нижний угол стартового экстента совсем не обязательно получается из SMin, надо выбрать минимальное значение. То же с правым верхним углом.
- Стартовый экстент может быть заметно больше поискового, если не повезет, он окажется максимальным экстентом слоя (пустой префикс).
- Для Z-кривой можно сделать оптимизацию и стартовый экстент приравнять к поисковому. Это возможно благодаря особенности z-кривой — для любого прямоугольника его левый нижний угол даёт минимальное значение ключа, а правый верхний — максимальное (в прямоугольнике). Да, такой стартовый экстент может содержать больше одного интервала значений, но это в дальнейшем устраняется фильтрацией.
- вычисляем значения ключа для левой нижней и правой верхней точек поискового экстента (KMin, KMax)
- заносим стартовый экстент в стек подзапросов
- пока стек подзапросов не пуст
- достаём верхний элемент
- если он не пересекается с поисковым экстентом, отбрасываем его, пропускаем итерацию. Это на случай, если стартовый экстент больше поискового и нам надо игнорировать лишнее
- если минимальная точка подзапроса находится внутри поискового экстента, делаем запрос к индексу по значению этой точки. В результате получаем два значения — “первый ключ” >= искомому и “последний ключ” на физической (листовой) странице, где лежит “первый ключ”
- если “первый ключ” > максимального значения текущего подзапроса, игнорируем текущий подзапрос, пропускаем итерацию
- если подзапрос целиком находится внутри поискового экстента, вычитываем его траверзом индекса от минимального до максимального значения, конец итерации
- если “последний ключ” > максимального значения текущего подзапроса, значит все данные текущего подзапроса лежат на этой странице, необходимо прочитать страницу до конца и отфильтровать ненужное, конец итерации
- отдельный случай “последний ключ” == максимальному значению текущего подзапроса, обрабатывается отдельно траверзом вперёд
- если “первый ключ” > максимального значения текущего подзапроса, игнорируем текущий подзапрос, пропускаем итерацию
- расщепляем текущий подзапрос
- добавляем к его префиксу 0 и 1 — получаем два новых префикса
- заполняем остаток ключа 0 или 1 — получаем минимальные и максимальные значения новых подзапросов
- заносим их в стек, сначала тот, что дополнили 1, затем 0. Это для однонаправленности чтения индекса.
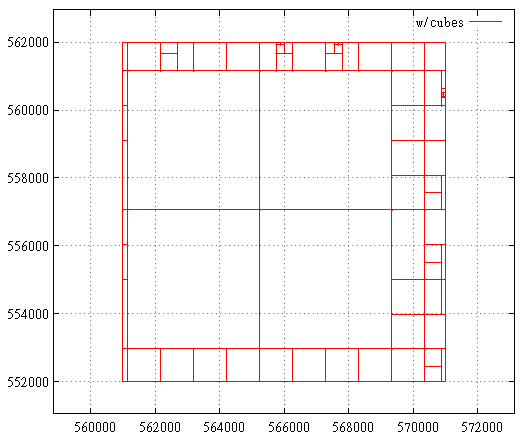
Фиг. 20 — разбиение на подзапросы в случае Z-кривой
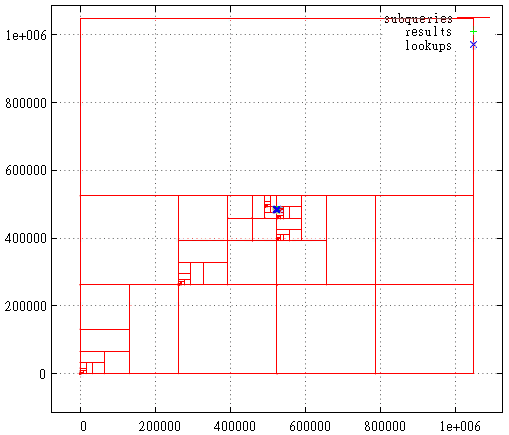
Фиг. 21 Кривая Гильберта, тот случай, когда стартовый экстент — максимальный
Здесь показана первая стадия — отрезание лишнего от максимального экстента слоя.

Фиг. 22 Кривая Гильберта, область поискового запроса
А здесь показано разбиение на подзапросы, найденные точки и обращения к индексу в области поискового запроса. Это всё же весьма неудачный с точки зрения кривой Гильберта запрос. Обычно всё куда как менее кроваво.
Тем не менее, статистика запросов говорит, что (грубо) на одних и тех же данных двумерный индекс на основе кривой Гильберта в среднем читает на 5% меньше дисковых страниц, но работает наполовину медленнее. Замедление вызвано еще и тем, что само вычисление (прямое и обратное) данной кривой намного тяжелее — 2000 тактов процессора у Гильберта по сравнению с 50 у Z-кривой.
Перестав поддерживать кривую Гильберта, можно было бы упростить алгоритм, на первый взгляд такое замедление ничем не оправдано. С другой стороны, это всего-лишь двумерный случай, например, в 8-мерном пространстве или более, статистика может заиграть совершенно новыми красками. Этот вопрос еще ждёт своего прояснения.
P.S.: Z-кривую иногда называют bit-interleaving-кривой из за алгоритма вычисления значения — разряды каждой из координат попадают в значение ключа через один, что весьма технологично. Но можно ведь перемежать разряды не по одиночке, а пачками по 2,3… 8… штук. Вот если брать по 8 разрядов, то на 32-разрядном ключе получим аналог 4-уровневого GRID-индекса от MS SQL. А в крайнем случае — одна пачка по 32 разряда — алгоритм строчной развёртки.
Такой индекс (не строчный, конечно) может быть весьма эффективен, даже эффективнее Z-кривой на каких-то наборах данных. К сожалению, за счет потери общности.
P.P.S.: Описанный индекс очень похож на работу с квадродеревом. Максимальный экстент — корневая страница квадродерева, у него 4 потомка … А следовательно, алгоритм можно отнести к “методам с прямым доступом”.
Отличия всё же есть и принципиальные.
Квадродерево нигде не хранится, оно виртуальное, заложено в самой природе чисел. Нет никаких ограничений на глубину дерева, информацию о населенности потомков мы получаем из населенности основного дерева. Причем, чтение основного дерева идет один раз, мы проходим его от наименьших значений к старшим. Забавно, но физическая структура B-дерева даёт возможность избегать пустопорожних запросов и ограничивать глубину рекурсии.
Еще одно — на каждой итерации появляется только два потомка — из них могут быть порождены 4 подзапроса, а могут быть и не порождены, если под ними нет данных. В 3-мерном случае мы бы говорили о 8 потомках, в 8-мерном — о 256.
P.P.P.S.: в начале этой статьи говорилось о дихотомии при поиске в многомерном индексе — чтобы получить логарифмическую стоимость, необходимо на каждой итерации делить примерно на равные части какой-то конечный ресурс — либо пространство значений ключей, либо пространство поиска. В представленном алгоритме эта дихотомия схлопнулась — мы одновременно делим и ключ и пространство.
“Я живу в обоих дворах, и мои деревья всегда выше.”(C)
P.P.P.P.S.: Как только ни называют Z-кривую, тут тебе и Z-order и bit-interleaving и код/кривая Мортона. А также она известна как кривая Лебега, так что в целях поддержания баланса, автор озаглавил статью в том числе в честь Анри Леона Лебега.
P.P.P.P.P.S.: На заглавной иллюстрации вид на ледник Федченко, просто красиво, да и пустоты хватает. На самом деле, автор был впечатлён тем, как разные идеи и методы плавно перетекают друг в друга, сливаясь постепенно в одном алгоритме. Подобно тому, как множество небольших источников воды, составляющих водосборный бассейн, образуют единый сток.