Всё содержание этой статьи является следствием решения задачи уровня первого года институтского курса математического анализа.
Здесь мы вводим новое произведение для решетчатых функций (мы будем называть его эпсилон-умножением), что дает нам возможность увидеть интересную связь между интегрально-дифференциальными уравнениями (в том числе и нелинейными) и рекуррентными соотношениями. Это позволяет с необычного ракурса взглянуть на некоторые методы их решения.
Но, что мне показалось особенно интересным, это то, что новое произведение также позволяет нам «порассуждать» о таких фундаментальных вещах, как непрерывность пространства-времени. Это рассуждение, конечно, нужно рассматривать, скорее, как интеллектуальное упражнение.
Мне показалось, что этот математический ребус или, если хотите, небольшое математическое путешествие на уровне знаний первого-второго курса технического ВУЗа может заинтересовать читателей Хабра, интересующихся математикой.
В этой статье речь будет идти о двух типах функций (определенных в области действительных чисел): аналитических и решетчатых.
Одна из основных целей введения этих операций проста — сохранить свойства производной произведения функций:

Что в случае решетчатых функций ( ) будет выглядеть как
) будет выглядеть как

где — левый оператор эпсилон-производной
— левый оператор эпсилон-производной
 — эпсилон-умножение
— эпсилон-умножение
Это позволит нам (по аналогии, например, с преобразованием Лапласа) ввести новое преобразование, которое мы будем называть эпсилон-преобразованием. Это даст нам возможность преобразовывать в общем случае нелинейные интегрально-дифференциальные уравнения в рекуррентные выражения и решать их (численно или аналитически), соответственно, рекуррентными методами.
 ), все наши эпсилон-функции, эпсилон-операции и рекуррентные уравнения стремятся к «обычным» функциям (аналитическим справа от нуля), обычным операциям между ними и обычным интегрально-дифференциальным уравнениям.
), все наши эпсилон-функции, эпсилон-операции и рекуррентные уравнения стремятся к «обычным» функциям (аналитическим справа от нуля), обычным операциям между ними и обычным интегрально-дифференциальным уравнениям.
Но тогда, это наводит на фундаментальный вопрос: а не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?
Так, например, говоря о времени, при достаточно малом шаге (например, порядка Планковского времени сек) эпсилон-уравнение Шредингера c
сек) эпсилон-уравнение Шредингера c  для временных процессов с характерным временем
для временных процессов с характерным временем  (или в области частот с частотами
(или в области частот с частотами  ) будет давать тот же результат, что и обычное уравнение Шредингера, но при этом, естественным образом вводится квантование времени.
) будет давать тот же результат, что и обычное уравнение Шредингера, но при этом, естественным образом вводится квантование времени.
В принципе, аналогичное рассуждение возможно и для пространства.
Решетчатая функция и множество
Решетчатые функции — это функции, определенные на дискретном множестве действительных чисел с постоянным шагом. Мы будем рассматривать только функции, определенные на множестве , где
, где  ,
,  . Так, например, такой функцией будет
. Так, например, такой функцией будет  , где
, где  — целое неотрицательное число. При этом
— целое неотрицательное число. При этом  . Будем обозначать множество таких функций через
. Будем обозначать множество таких функций через  . Все решетчатые функции, которые мы будем рассматривать ниже будут принадлежать этому множеству
. Все решетчатые функции, которые мы будем рассматривать ниже будут принадлежать этому множеству  .
.
Пример решетчатой функции
Функция , где
, где  :
:
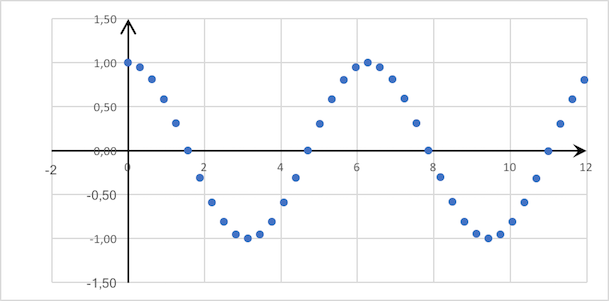
Эпсилон-производная
Будем называть эпсилон-производной функции в
в  следующую величину:
следующую величину:

Соответственно, функцию, значение которой в для любого
для любого  равно эпсилон-производной функции
равно эпсилон-производной функции  в
в  , мы будем называть эпсилон-производной функции
, мы будем называть эпсилон-производной функции  и обозначать как
и обозначать как  (или просто
(или просто  ).
).
Очевидно, что функция
 и поэтому по отношению к ней можно еще раз применить эпсилон дифференцирование, и т.д. Мы будем обозначать символом
и поэтому по отношению к ней можно еще раз применить эпсилон дифференцирование, и т.д. Мы будем обозначать символом 
 -ю
-ю  -производную функции. По индукции легко доказывается, что
-производную функции. По индукции легко доказывается, что

Эпсилон-интегрирование
Процедуру, обратную эпсилон-дифференцированию, назовем соответственно эпсилон-интегрированием. Функцию , значение которой в
, значение которой в  для любого
для любого 

будем называть эпсилон-первообразной функции .
.
Эпсилон производная произведения
К сожалению, эпсилон-производная не обладает свойствами обычной производной. Так, например, очевидно, что в общем случае

Часть отличает эту «производную» от обычной производной произведения дифференцируемых функций. В случае решения численными методами нелинейных дифференциальных уравнений это дает дополнительную погрешность в вычислениях.
отличает эту «производную» от обычной производной произведения дифференцируемых функций. В случае решения численными методами нелинейных дифференциальных уравнений это дает дополнительную погрешность в вычислениях.
Теперь давайте представим, что у нас не было бы этого дополнительного члена. Чтобы нам это могло дать?
По крайней мере, мы могли бы применять некоторые методы решения дифференциальных уравнений для решения рекуррентных уравнений (уравнений с функциями из множества ). Например, мы имели бы разложение в ряд Тейлора, мы смогли бы пользоваться интегрированием (эпсилон-интегрированием) по частям, применять преобразования (эпсилон-преобразование) Лапласа. Но в действительности все даже интереснее, и этому и посвящена данная статья.
). Например, мы имели бы разложение в ряд Тейлора, мы смогли бы пользоваться интегрированием (эпсилон-интегрированием) по частям, применять преобразования (эпсилон-преобразование) Лапласа. Но в действительности все даже интереснее, и этому и посвящена данная статья.
Но как избавиться от этого дополнительного элемента? Мы можем создать, например, другое умножение (эпсилон-умножение).
Базовая задача
Это именно та задача, следствием решения которой и является вся эта статья.
Мы хотим найти такую формулу для эпсилон-произведения , чтобы удовлетворялись следующие требования:
, чтобы удовлетворялись следующие требования:
Всем этим свойствам удовлетворяет функция , определяемая как (все три формулы эквивалентны):
, определяемая как (все три формулы эквивалентны):


 ,
,
где — биномиальный коэффициент Ньютона:
— биномиальный коэффициент Ньютона:  , (
, ( )
)
Чтобы немного освоиться с новым произведением, рассмотрим несколько примеров.
Эпсилон-ряд Тейлора
Теперь мы имеем полный аналог разложения Тейлора:

Будем называть этот ряд эпсилон-рядом Tейлора, а само разложение — эпсилон-разложением в ряд Tэйлора.
Определение. (Эпсилон преобразование)
Пусть такое, что на множестве
такое, что на множестве  ряд Tэйлора функции
ряд Tэйлора функции  в правой окрестности нуля сходится к самой функции. Тогда функцию
в правой окрестности нуля сходится к самой функции. Тогда функцию  мы будем называть аналитической функцией в нуле справа. Тогда функции
мы будем называть аналитической функцией в нуле справа. Тогда функции  и
и  будем называть эпсилон-сопряженными, если для любого целого или нулевого
будем называть эпсилон-сопряженными, если для любого целого или нулевого 
 -ая производная справа функции
-ая производная справа функции  в нуле равняется
в нуле равняется  -ой эпсилон-производной функции
-ой эпсилон-производной функции  в нуле.
в нуле.

Функцию тогда будем называть эпсилон-образ
тогда будем называть эпсилон-образ  или в случае, если эта функция имеет название (например, cos), то будем называть просто эпсилон-'название функции' (например, эпсилон-косинус) и обозначать как
или в случае, если эта функция имеет название (например, cos), то будем называть просто эпсилон-'название функции' (например, эпсилон-косинус) и обозначать как  ''обозначение функции'' (
''обозначение функции'' ( cos). Функцию
cos). Функцию  будем называть эпсилон-прообраз функции
будем называть эпсилон-прообраз функции  .
.
Эпсилон-преобразования операций
В данной таблице и в следующей функции и
и  , а также
, а также  и
и  — попарно эпсилон-сопряженные, то есть
— попарно эпсилон-сопряженные, то есть


Тогда операции преобразовываются (в результате эпсилон-преобразования) следующим образом:














 (эпсилон-первообразная)
(эпсилон-первообразная)
Эпсилон-преобразование некоторых аналитических функций




















 (для
(для  )
)
Разложение в эпсилон-ряд Тейлора

Эта формула становится очевидной, если мы заметим, что оператор является оператором смещения на
является оператором смещения на  шагов:
шагов:

Эпсилон-преобразование Лапласа
Мы можем также ввести эпсилон-преобразование Лапласа и пользоваться им также, как и обычным преобразованием Лапласа но применительно к решетчатым функциям , но это выходит за рамки целей данной статьи.
, но это выходит за рамки целей данной статьи.
В силу вышесказанного мы можем записать, например, аналоги тригонометрических формул







Но все же эпсилон-косинус и эпсилон-синус не обладают в отличии от обычного косинуса и синуса одной важной чертой — они не периодичны. Действительно,


Также

при этом функции и
и  — периодические функции с периодом
— периодические функции с периодом  . Поэтому функции
. Поэтому функции  и
и  — не периодические функции, с нулями в точках
— не периодические функции, с нулями в точках  и
и  соответственно, при этом ''размах'' между минимумами и максимумами при увлечении
соответственно, при этом ''размах'' между минимумами и максимумами при увлечении  возрастает как
возрастает как  .
.
Обратное эпсилон-преобразование можно осуществить просто устремив
Это можно сформулировать более строго в виде теоремы, которую я приведу без доказательства.
Теорема
Пусть функции и
и  — эпсилон-сопряженные для любого
— эпсилон-сопряженные для любого  . Тогда, при стремлении
. Тогда, при стремлении  , при условии, что
, при условии, что  (где
(где  имеет тот же смысл, что и в определении эпсилон-отображения ), значение
имеет тот же смысл, что и в определении эпсилон-отображения ), значение  на множестве
на множестве  стремится к
стремится к  , то есть
, то есть

Все сказанное выше наводит на фундаментальный вопрос: a не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?
Рассмотрим, например, одномерное уравнение Шредингера:

Это уравнение предполагает непрерывность пространства-времени и возможность бесконечно малой величины и
и  (это неявно принимается, если мы используем дифференцирование). Если говорить о времени, то это подразумевает бесконечную энергию, что противоречит современным представлениям о вселенной.
(это неявно принимается, если мы используем дифференцирование). Если говорить о времени, то это подразумевает бесконечную энергию, что противоречит современным представлениям о вселенной.
Чтобы не усложнять рассуждения, давайте рассмотрим случай когда не зависит от
не зависит от  . В этом случае
. В этом случае  можно записать в виде:
можно записать в виде:

Но ведь — это аналитическая функция, значит мы можем применить к ней наш подход, то есть мы можем сделать эпсилон-преобразование (относительно времени) нашего исходного уравнения Шредингера и мы получим
— это аналитическая функция, значит мы можем применить к ней наш подход, то есть мы можем сделать эпсилон-преобразование (относительно времени) нашего исходного уравнения Шредингера и мы получим


При этом

То есть при очень меленьком шаге времени (кванте времени) не существенном для наших расчетов, мы не увидим разницы между решением (обычного) уравнения Шредингера и решением эпсилон-уравнения Шредингера.
не существенном для наших расчетов, мы не увидим разницы между решением (обычного) уравнения Шредингера и решением эпсилон-уравнения Шредингера.
Но тогда это значит, что мы не можем в действительности сказать, какое произведение является «истинным» («используется» природой) — наше обычное или эпсилон-произведение (с достаточно малым квантованием времени).
При этом в случае эпсилон-произведения (и соответственно эпсилон-уравнения Шредингера и его эпсилон-волнового решения), мы имеем очевидный плюс — квантование времени становится естественным, и мы не сталкиваемся с требованием бесконечной энергии. Фактически мы имеем все то же уравнение, с теми же решениями, но при этом естественным образом устраняем необходимость допущения непрерывности времени.
Итак, если время дискретно с «шагом» , а ''истинным'' умножением является эпсилон-умножение с шагом дискретности времени, то как это может проявиться? Можно ли поставить мысленный или реальный эксперимент и понять, какое произведение является «истинным» и какой шаг (квант) при этом используется?
, а ''истинным'' умножением является эпсилон-умножение с шагом дискретности времени, то как это может проявиться? Можно ли поставить мысленный или реальный эксперимент и понять, какое произведение является «истинным» и какой шаг (квант) при этом используется?
Можно привести некоторые оценки, для понимания насколько сильно изменились бы наши представления о мире, если «истинным» было бы именно «эпсилон-умножение» (а не обычное умножение).
Вспомним, что

Тогда для имеем:
имеем:
Давайте грубо оценим, способны ли мы заметить это отличие?
Пример 1. Изменения за время жизни вселенной
Предположим, что наша временная дискретность сравнима с Планковским временем:
 сек.
сек.
Время жизни вселенной:
 сек.
сек.
Найдем для каких частот за время жизни вселенной амплитуда колебаний могла измениться, например, на 0,5%.
за время жизни вселенной амплитуда колебаний могла измениться, например, на 0,5%.

 рад/сек
рад/сек
Это значит, что для частот порядка 1 TГц (или для частиц с энергией эВ) за время жизни вселенной амплитуда (волновой функции) изменилась бы на порядка один процент (порядок). То есть понятно, что как минимум в обычной жизни мы никак не можем это увидеть.
эВ) за время жизни вселенной амплитуда (волновой функции) изменилась бы на порядка один процент (порядок). То есть понятно, что как минимум в обычной жизни мы никак не можем это увидеть.
Пример 2. Изменения за секунду
Давайте оценим во сколько раз изменится амплитуда волновой функции частицы с ультравысокой энергией порядка эВ за одну секунду.
эВ за одну секунду.
 эв по порядку соответствует
эв по порядку соответствует  Гц
Гц

То есть за секунду амплитуда волновой функции такой частицы увеличится в 100 тысяч раз (порядок).
Выглядит существенным. Но как это обнаружить? Дело в том, что физический смысл имеет не сама волновая функция, а , а в случае эпсилон-образа это будет
, а в случае эпсилон-образа это будет  . Но
. Но

Что говорит о том, что как раз величина, которая имеет физический смысл меняться не будет, и данный подход не позволит нам ответить на поставленный вопрос.
Здесь мы вводим новое произведение для решетчатых функций (мы будем называть его эпсилон-умножением), что дает нам возможность увидеть интересную связь между интегрально-дифференциальными уравнениями (в том числе и нелинейными) и рекуррентными соотношениями. Это позволяет с необычного ракурса взглянуть на некоторые методы их решения.
Но, что мне показалось особенно интересным, это то, что новое произведение также позволяет нам «порассуждать» о таких фундаментальных вещах, как непрерывность пространства-времени. Это рассуждение, конечно, нужно рассматривать, скорее, как интеллектуальное упражнение.
Мне показалось, что этот математический ребус или, если хотите, небольшое математическое путешествие на уровне знаний первого-второго курса технического ВУЗа может заинтересовать читателей Хабра, интересующихся математикой.
Замечание
- вы не увидите никаких ссылок и, вообще, всё это результат размышлений отдельно взятого человека
- возможно (и даже скорее всего), всё это и не ново, и, возможно, некоторые термины, которые я использую не соответствуют математической традиции, но так как это не научная публикация, здесь нет претензии на новизну и всё это довольно просто, то это терминологическое отличие, на мой взгляд, не является чем-то действительно важным
Краткое изложение
В этой статье речь будет идти о двух типах функций (определенных в области действительных чисел): аналитических и решетчатых.
Замечание 1
Точнее речь будет идти об аналитических справа от нуля функциях, которые мы будем обозначать заглавными буквамии о решетчатых функциях, определенных на множестве целых неотрицательных чисел (
), для обозначения которых мы будем использовать строчные буквы
. Множество таких решетчатых функций мы будем обозначать как
. Точные определения этих функций будут приведены ниже в данной статье
Замечание 2Мы установим взаимно однозначное соответствие между функциями из этих двух классов. Мы также введем новые операции для решетчатых функций. Эти операции будут аналогичны «обычным» операциям над «обычными» функциями. Мы будем отличать эти новые операции добавлением приставки «эпсилон». Так «обычной» производной будет соответствовать эпсилон-производная, обычному произведению — эпсилон-произведение, обычному интегрированию — эпсилон-интегрирование и т.д. При этом, если операция остается неизменной (как в случае суммирования и вычитание) название меняться не будет.
Иногда, в примерах мы будем расширять наш подход и на область комплексных чисел. Строго говоря, это должно быть обосновано. Но я опускаю это обоснование (как и доказательства некоторых других утверждений), чтобы не перегружать и так длинную статью
Одна из основных целей введения этих операций проста — сохранить свойства производной произведения функций:
Что в случае решетчатых функций (
где
Это позволит нам (по аналогии, например, с преобразованием Лапласа) ввести новое преобразование, которое мы будем называть эпсилон-преобразованием. Это даст нам возможность преобразовывать в общем случае нелинейные интегрально-дифференциальные уравнения в рекуррентные выражения и решать их (численно или аналитически), соответственно, рекуррентными методами.
ЗамечаниеВажным фактом при этом является то, что при стремлении шага решетчатой функции к нулю (
Также справедливо и обратное: мы получаем возможность решать рекуррентные соотношения методами интегрально-дифференциальных уравнений
Но тогда, это наводит на фундаментальный вопрос: а не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?
Так, например, говоря о времени, при достаточно малом шаге (например, порядка Планковского времени
В принципе, аналогичное рассуждение возможно и для пространства.
Обозначения, используемые в статье
 — строчными буквами мы будем обозначать решетчатые функции, определенные на множестве
— строчными буквами мы будем обозначать решетчатые функции, определенные на множестве  , где
, где  ,
,  . В зависимости от контекста
. В зависимости от контекста  (или подобное, например,
(или подобное, например,  ) может быть или обозначением самой решетчатой функции или значением этой функции в точке
) может быть или обозначением самой решетчатой функции или значением этой функции в точке 
 — множество всех функций
— множество всех функций  определенных выше
определенных выше
 — иногда, для обозначения функции
— иногда, для обозначения функции  для простоты будем писать просто
для простоты будем писать просто 
 — заглавными буквами мы будем обозначать «обычные» функции. Все подобные функции в данной статье будут аналитическими справа от нуля функциями (определение будет дано ниже в статье)
— заглавными буквами мы будем обозначать «обычные» функции. Все подобные функции в данной статье будут аналитическими справа от нуля функциями (определение будет дано ниже в статье)
 — шаг решетчатой функции:
— шаг решетчатой функции:  . В зависимости от контекста
. В зависимости от контекста  может быть или обозначением самой решетчатой функции или значением этой функции в точке
может быть или обозначением самой решетчатой функции или значением этой функции в точке 
 — левый оператор, обозначающий производную дифференцируемой функции:
— левый оператор, обозначающий производную дифференцируемой функции: 
 — левый оператор, обозначающий эпсилон-производную решетчатой функции:
— левый оператор, обозначающий эпсилон-производную решетчатой функции: 
 — левый оператор, введенный для удобства записи некоторых выражений, и обозначающий производную дифференцируемой функции, применяемый только к функции
— левый оператор, введенный для удобства записи некоторых выражений, и обозначающий производную дифференцируемой функции, применяемый только к функции  (или к производной функции
(или к производной функции  любого порядка) в произведении функций, например,
любого порядка) в произведении функций, например,


 — единичный левый оператор для решетчатой функции:
— единичный левый оператор для решетчатой функции: 
 — эпсилон-производная решетчатой функции:
— эпсилон-производная решетчатой функции:

 — левый оператор, введенный для удобства записи некоторых выражений, и обозначающий эпсилон-производную решетчатой функции, применяемый только к решетчатой функции
— левый оператор, введенный для удобства записи некоторых выражений, и обозначающий эпсилон-производную решетчатой функции, применяемый только к решетчатой функции  (или эпсилон-производной функции
(или эпсилон-производной функции  любого порядка) в произведении (обычном) решетчатых функций, например,
любого порядка) в произведении (обычном) решетчатых функций, например,


 — эпсилон произведение
— эпсилон произведение
 —
—  -ая эпсилон-степень функции
-ая эпсилон-степень функции  . Так, например,
. Так, например, 
 —
—  -ая эпсилон-производная функции
-ая эпсилон-производная функции  . Так, например,
. Так, например, 
 — эпсилон-преобразование (прямое)
— эпсилон-преобразование (прямое)
Если , то
, то  и
и  являются эпсилон-сопряженными, при этом
являются эпсилон-сопряженными, при этом  является эпсилон-образом
является эпсилон-образом  и
и  — эпсилон-прообразом
— эпсилон-прообразом 
 — обратное эпсилон-преобразование
— обратное эпсилон-преобразование
Если
Краткая логика статьи
Здесь изложена логическая структура статьи. Кому-то этого будет достаточно для понимания всей статьи и таким образом сохранит его время.
Далее каждый из этих пунктов рассматривается более детально
- Мы будем рассматривать решетчатые функции
,…, определенные на множестве
, где
,
.
Замечание
При этомможет быть любым положительным действительным числом. Поэтому иногда в примерах, в тех случаях, когда мы не используем стремление
, мы принимаем для простоты
- Назовем эпсилон дифференцированием следующий левый оператор:
, где
— шаг решетчатой функции
- Введем новое произведение, которое будем называть эпсилон-произведением и обозначать как
.
Здесь три эквивалентные формулы для эпсилон-произведения:
где— биномиальный коэффициент Ньютона:
, (
)
Его основные свойства:
- свойства обычного умножения, такие как коммутативность, ассоциативность, дистрибутивность, существование единицы (единственной) и нулевого элемента (единственного)
- для производной эпсилон-произведения решетчатых функций мы имеем ту же формулу, что и для производной произведения (обычных) дифференцируемых функций:
- при стремлении
(шаг решетчатой функции) эпсилон-произведение стремится к обычному произведение
, где
и
соответственно функции, к которым стремятся решетчатые функции
и
при
, то есть:
Замечание
Позже будет показано чтои
, а также
и
являются попарно эпсилон-сопряженными
- Вводим эпсилон-ряд Тейлора. Он будет аналогичен обычному ряду Тейлора, но произведение, возведение в степень и производные должны быть заменены на эпсилон-произведение, эпсилон-степень и эпсилон-производные:
- Введение эпсилон-ряда Тейлора позволяет нам ввести эпсилон-функции, аналогичные аналитическим функциям (например, эпсилон-тригонометрические функции). Для этого потребуем, чтобы эпсилон-производные в нуле (всех порядков) для этих эпсилон-функций равнялись производным в нуле (справа) для обычных функций. Для обозначения эпсилон-функции мы будем добавлять приставку
. Так, например, для эпсилон-экспоненты получим:
- Введем понятие эпсилон преобразования. Суть этого преобразования заключается в замене всех операций (производная, умножение, возведение в степень) на эпсилон-операции а всех функций на эпсилон-функции. При данном преобразовании тождества будут сохраняться. Так, например, для эпсилон-тригонометрических функций все тождества будут аналогичны обычным тригонометрическим тождествам. Например,
Если эпсилон преобразование обозначить через, то этот факт можно записать, как
Эпсилон-функцию мы также будем называть эпсилон-образом. Так эпсилон-косинус является эпсилон-образом косинуса. При этом сам косинус является эпсилон-прообразом для эпсилон-косинуса. При этом эти две функции (например, эпсилон-косинус и косинус) являются эпсилон-сопряженными. - Соответственно, обратное эпсилон-преобразование — это преобразование обратное (прямому) эпсилон-преобразованию. Будем обозначать его, как
.
- Таким образом, через прямые и обратные эпсилон-преобразования мы устанавливаем соответствие между дифференциальными уравнениями (ДУ) (в том числе и нелинейными) и рекуррентными соотношениями (РС).
Теперь для решения нелинейных дифференциальных уравнений мы можем применить следующую схему:
ДУРС
(решение РС)
(решение ДУ)
То есть, мы делаем эпсилон-преобразование исходного ДУ, получаем РC, решаем его и делаем обратное эпсилон-преобразование, получая таким образом решение дифференциального уравнения. Важно понимать, что таким образом будут найдены лишь решения, являющиеся функциями, аналитическими справа от нуля. Это тот же подход, что применяется при решении, например, линейных дифференциальных уравнений с помощью преобразований Лапласа. - Аналогично, рекуррентные уравнения можно привести к дифференциальным и решать их соответствующими методами. В этом случае мы имеем следующую схему:
РCДУ
(решение ДУ)
(решение РC)
- Также легко можно ввести и дополнительные операции, и преобразования, например, эпсилон-интегрирование и эпсилон-преобразование Лапласа
- В статье приводятся три примера
- решение линейного дифференциального уравнения гармонических колебаний
- решение нелинейного дифференциального уравнения (Бесселя)
- решение линейного рекуррентного уравнения (формула для чисел Фибоначчи)
- При стремлении
(шаг решетчатой функции) эпсилон-функции и эпсилон-операторы стремятся к своим прообразам. Так, например, при стремлении
эпсилон произведение стремится к обычному произведению, эпсилон-производная — к обычной производной,… эпсилон-косинус — к обычному косинусу, эпсилон-синус к обычному синусу… Это значит, что обратное эпсилон-преобразование может быть выполнено обычным стремлением
. Этот факт позволяет нам рассматривать дифференциально-интегральные уравнения (в том числе и нелинейные) с решениями аналитическими справа от нуля, как предельный случай рекуррентных уравнений с шагом
.
- Это наводит на мысль о том, а не является ли эпсилон-умножение «истинным» умножением (во всяком случае в некоторых случаях) в нашем физическом мире? Так, например, рассмотрим одномерное уравнение Шредингера:
Это уравнение предполагает непрерывность пространства времени и возможность бесконечно малой величиныи
(что заложено в том факте, что мы используем дифференцирование), что в случае квантовой механики подразумевает бесконечную энергию, что невозможно.
Но давайте рассмотрим эпсилон-преобразование этого уравнения (заменив производные на эпсилон-производные, функции на решетчатые эпсилон-функции, произведение — на эпсилон-произведение, ...). При достаточно маломмы получим решения очень близкие к тем, которые мы бы получили при решении изначального уравнения Шредингера. При этом естественным образом вводится дискретность пространства-времени, что устраняет проблему бесконечной энергии.
- Это в свою очередь ставит вопрос о том, как можно проверить, а какое же умножение является «истинным» в нашем физическом мире, обычное или эпсилон-умножение? Возможно ли поставить мыслительный или физический эксперимент для ответа на этот вопрос?
Далее каждый из этих пунктов рассматривается более детально
Решетчатые функции и эпсилон-производная
Решетчатая функция и множество
Решетчатые функции — это функции, определенные на дискретном множестве действительных чисел с постоянным шагом. Мы будем рассматривать только функции, определенные на множестве
Пример решетчатой функции
Функция
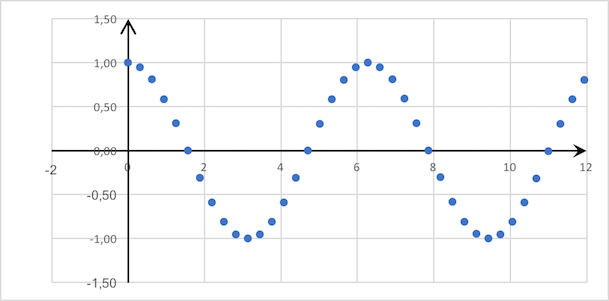
Эпсилон-производная
Будем называть эпсилон-производной функции
Соответственно, функцию, значение которой в
Очевидно, что функция
Эпсилон-интегрирование
Процедуру, обратную эпсилон-дифференцированию, назовем соответственно эпсилон-интегрированием. Функцию
будем называть эпсилон-первообразной функции
Эпсилон производная произведения
К сожалению, эпсилон-производная не обладает свойствами обычной производной. Так, например, очевидно, что в общем случае
Часть
Замечание
Это дополнительное слагаемое приводит также, в частности, к тому, что мы не можем применить обычную формулу Тейлора для разложения решетчатой функции в ряд
Теперь давайте представим, что у нас не было бы этого дополнительного члена. Чтобы нам это могло дать?
По крайней мере, мы могли бы применять некоторые методы решения дифференциальных уравнений для решения рекуррентных уравнений (уравнений с функциями из множества
Но как избавиться от этого дополнительного элемента? Мы можем создать, например, другое умножение (эпсилон-умножение).
Базовая задача
Это именно та задача, следствием решения которой и является вся эта статья.
Мы хотим найти такую формулу для эпсилон-произведения
- выполнялись бы свойства обычного умножения, такие, как коммутативность, ассоциативность, дистрибутивность, существование единицы (единственной) и нулевого элемента (единственного)
- для эпсилон-производной эпсилон-произведения решетчатых функций мы должны иметь ту же формулу, что и для производной произведения (обычных) дифференцируемых функций, то есть
- при стремлении
(шаг решетчатой функции) эпсилон-произведение должно стремиться к обычному произведение
, где
и
соответственно функции, к которым стремятся решетчатые функции
и
при
, то есть:
Эпсилон-умножение
Всем этим свойствам удовлетворяет функция
где
Замечание
Чтобы не перегружать статью мы не будем приводить доказательства, но первые два свойства доказываются легко, последнее — не так очевидно
Чтобы немного освоиться с новым произведением, рассмотрим несколько примеров.
Пример 1. (умножение на число)
Если для некоторой функции  все элементы
все элементы  , где
, где  — любое действительное число, то для любой функции
— любое действительное число, то для любой функции  элементы эпсилон-произведения
элементы эпсилон-произведения  равны
равны  .
.
Это легко можно увидеть из первой формулы эпсилон-умножения.
Как результат мы получаем, что единичным элемент эпсилон-умножения является функция все элементы которой равны 1, а нулевым элементом — со всеми элементами равными 0.
все элементы которой равны 1, а нулевым элементом — со всеми элементами равными 0.
Это легко можно увидеть из первой формулы эпсилон-умножения.
Как результат мы получаем, что единичным элемент эпсилон-умножения является функция
Пример 2. (эпсилон степень)
Из определения эпсилон-произведения легко найти эпсилон-степень  , которая является эпсилон-аналогом (в следующей главе будет введено определение эпсилон-образа) функции
, которая является эпсилон-аналогом (в следующей главе будет введено определение эпсилон-образа) функции  :
:

Таким образом получаем, что эпсилон-аналог (далее будет введено понятие эпсилон-образа) функции является функция
является функция 
Так, например,


Очевидно, что равна нулю для
равна нулю для 
Теперь формула для эпсилон-производных эпсилон-степени находится в полном соответствии с обычной производной обычной степени, так например,
Таким образом получаем, что эпсилон-аналог (далее будет введено понятие эпсилон-образа) функции
Так, например,
Очевидно, что
Теперь формула для эпсилон-производных эпсилон-степени находится в полном соответствии с обычной производной обычной степени, так например,
Замечание
В последней формуле пропущено, что не является проблемой, т.к.
может быть любым (
,
), в том числе и 1. Конечно, мы не должны забывать про
, если исследуется зависимость от него, например, при
Эпсилон-ряд Тейлора
Теперь мы имеем полный аналог разложения Тейлора:
Будем называть этот ряд эпсилон-рядом Tейлора, а само разложение — эпсилон-разложением в ряд Tэйлора.
Эпсилон преобразование
Определение. (Эпсилон преобразование)
Пусть
Функцию
Пример 1. (Эпсилон-экспонента)
Найдем формулу для эпсилон-экспоненты, которую мы в соответствии с оговоренным правилом будем обозначать  . Пусть
. Пусть  произвольное комплексное число. Найдем функцию эпсилон-сопряженную функции
произвольное комплексное число. Найдем функцию эпсилон-сопряженную функции 

Заметим, что
При этом очевидно, что , поэтому предыдущее равенство мы будем записывать в виде (хотя эта запись и не совсем корректна):
, поэтому предыдущее равенство мы будем записывать в виде (хотя эта запись и не совсем корректна):

Такой вид записи мы будем использовать и для других эпсилон-функций.
Заметим, что
При этом очевидно, что
Такой вид записи мы будем использовать и для других эпсилон-функций.
Пример 2. (Эпсилон-косинус, эпсилон-синус)
Найдем формулу для эпсилон-косинуса и эпсилон-синуса.
Пусть — действительное число. Tогда
— действительное число. Tогда




Пусть
Пример 3. (Эпсилон-умножение на икс в эпсилон-степени)
Найдем эпсилон-ряд Тейлора для

где — неотрицательное целое число
— неотрицательное целое число
Найдем производные в нуле справа для функции

Тогда эпсилон-ряд Тейлора для эпсилон-сопряженной функции можно записать как

В дальнейшем будет показано, что эта формула справедлива также и для отрицательных целых , что значит, что эта формула справедлива для любых целых
, что значит, что эта формула справедлива для любых целых 
Найдем эпсилон-ряд Тейлора для
где
Найдем производные в нуле справа для функции
Тогда эпсилон-ряд Тейлора для эпсилон-сопряженной функции можно записать как
В дальнейшем будет показано, что эта формула справедлива также и для отрицательных целых
Эпсилон-преобразования операций
В данной таблице и в следующей функции
Тогда операции преобразовываются (в результате эпсилон-преобразования) следующим образом:
Эпсилон-преобразование некоторых аналитических функций
Разложение в эпсилон-ряд Тейлора
Эта формула становится очевидной, если мы заметим, что оператор
Эпсилон-преобразование Лапласа
Мы можем также ввести эпсилон-преобразование Лапласа и пользоваться им также, как и обычным преобразованием Лапласа но применительно к решетчатым функциям
Примеры эпсилон-преобразований для тригонометрических формул
В силу вышесказанного мы можем записать, например, аналоги тригонометрических формул
Но все же эпсилон-косинус и эпсилон-синус не обладают в отличии от обычного косинуса и синуса одной важной чертой — они не периодичны. Действительно,
Также
при этом функции
Замечание
Соответственно для эпсилон-экспоненты имеем
Примеры решения дифференциальных уравнений методом эпсилон-отображения
Пример 1. Гармонические колебания
Давайте начнем с решения линейных дифференциальных уравнений и в качестве примера возьмем уравнение гармонических колебаний:

Распишем процедуру решения по шагам.
Шаг 1. (Эпсилон преобразование)

Где .
.
Получили рекуррентное уравнение.
Далее, в зависимости от того, хотим ли мы найти приблизительное решение численными методами или хотим найти точное аналитическое решение, последовательность шагов может быть разной.
Если мы ищем точное решение, выраженное формулой, то последовательность шагов может быть следующей.
Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле всех порядков)
Находим формулу для -ой эпсилон-производной для нашего рекуррентного выражения и находим рекуррентное выражение для всех эпсилон-производных в нуле.
-ой эпсилон-производной для нашего рекуррентного выражения и находим рекуррентное выражение для всех эпсилон-производных в нуле.

Берем значение в нуле

Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)
Заметим, что ,
,  .
.
Будем для определенности считать, что начальное смещение , а начальная скорость
, а начальная скорость  . Тогда имеем:
. Тогда имеем:


Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)
Но тогда

Если же мы хотим решать численным методом (приблизительное решение), то
Шаг 2. Численное решение. (Находим значения )
)
 , начиная с 0. Чем больше значений будет найдено, тем больше коэффициентов ряда Тейлора нам будет известно, и, соответственно, тем точнее будет результат.
, начиная с 0. Чем больше значений будет найдено, тем больше коэффициентов ряда Тейлора нам будет известно, и, соответственно, тем точнее будет результат.
Для определенности, как и в предыдущем случае, будем считать, что начальное смещение , а начальная скорость 1. Имеем:
, а начальная скорость 1. Имеем:






…
Шаг 3. Численное решение. (Эпсилон-производные в нуле)






…
Шаг 4. Численное решение. (Ряд Тейлора для искомой функции)
Имея необходимое для точности наших вычислений количество (или все, если получилось найти аналитическую формулу) эпсилон производных в нуле, мы можем построить ряд Тейлора для эпсилон-сопряженной функции, что и будет решением:

Подставляя значения эпсилон производных для нашего случай получим

Таким образом мы можем с точностью до любого члена разложения в ряд Тейлора найти нашу искомую функцию.
Распишем процедуру решения по шагам.
Шаг 1. (Эпсилон преобразование)
Где
Получили рекуррентное уравнение.
Далее, в зависимости от того, хотим ли мы найти приблизительное решение численными методами или хотим найти точное аналитическое решение, последовательность шагов может быть разной.
Если мы ищем точное решение, выраженное формулой, то последовательность шагов может быть следующей.
Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле всех порядков)
Находим формулу для
Берем значение в нуле
Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)
Заметим, что
Будем для определенности считать, что начальное смещение
Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)
Но тогда
Если же мы хотим решать численным методом (приблизительное решение), то
Шаг 2. Численное решение. (Находим значения
ЗамечаниеРешаем последовательно для значений
Для наглядности в данном примере мы будем сохранятьи
в наших формулах, но в реальном численном расчёте вместо
должно быть подставлено его численное значение, а вместо
может быть подставлено любое положительное число
, например,
Для определенности, как и в предыдущем случае, будем считать, что начальное смещение
…
Шаг 3. Численное решение. (Эпсилон-производные в нуле)
…
Шаг 4. Численное решение. (Ряд Тейлора для искомой функции)
Имея необходимое для точности наших вычислений количество (или все, если получилось найти аналитическую формулу) эпсилон производных в нуле, мы можем построить ряд Тейлора для эпсилон-сопряженной функции, что и будет решением:
Подставляя значения эпсилон производных для нашего случай получим
Таким образом мы можем с точностью до любого члена разложения в ряд Тейлора найти нашу искомую функцию.
Замечание
В данном случае, конечно, не было особого смысла использовать эпсилон-преобразование, и мы привели это лишь, как пример, чтобы продемонстрировать подход
Пример 2. Уравнение Бесселя
Теперь давайте применим этот метод для решения для чего-то более интересного. Рассмотрим нелинейное дифференциальное уравнение, например, уравнения Бесселя.

Шаг 1. (Эпсилон преобразование)


Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле)
Будем считать
Берем -ую эпсилон-производную в нуле. Получаем формулу
-ую эпсилон-производную в нуле. Получаем формулу


Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)
Будем последовательно находить значения эпсилон-производных в нуле:
в нуле:



…

Пусть —
—  -ый коэффициент эпсилон-ряда Тейлора. Тогда предыдущее равенство можно записать в виде
-ый коэффициент эпсилон-ряда Тейлора. Тогда предыдущее равенство можно записать в виде

Мы видим, что если не целое число и не 0, то все коэффициенты ряда Tейлора равны 0. Если
не целое число и не 0, то все коэффициенты ряда Tейлора равны 0. Если  целое или ноль, то это говорит о том, что
целое или ноль, то это говорит о том, что  -тый коэффициент эпсилон-ряда Tейлора может быть не равен нулю и его выбор произволен и определяется требованиями нормировки. При этом для
-тый коэффициент эпсилон-ряда Tейлора может быть не равен нулю и его выбор произволен и определяется требованиями нормировки. При этом для  коэффициенты эпсилон-ряда Тейлора также не равны 0, а для
коэффициенты эпсилон-ряда Тейлора также не равны 0, а для  (
( — натуральное) — равны 0.
— натуральное) — равны 0.
Найдем — ые коэффициенты эпсилон-ряда Тейлора.
— ые коэффициенты эпсилон-ряда Тейлора.
Подставляя вместо
вместо  получим
получим

Тогда легко получить, что -ый член разложения в эпсилон-ряд Tэйлора имеет вид
-ый член разложения в эпсилон-ряд Tэйлора имеет вид

где -неотрицательное целое число, C-произвольное комплексное неравное нулю, определяемое требованиями нормировки
-неотрицательное целое число, C-произвольное комплексное неравное нулю, определяемое требованиями нормировки
Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)
Тогда для неотрицательных целых , принимая
, принимая  получим формулу
получим формулу

что соответствует известной формуле функции Бесселя первого рода для целых, неотрицательных .
.
Для всех других решений — не существует разложения в ряд Tэйлора в нуле.
Шаг 1. (Эпсилон преобразование)
Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле)
Будем считать
Берем
Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)
Будем последовательно находить значения эпсилон-производных
…
Пусть
Мы видим, что если
Найдем
Подставляя
Тогда легко получить, что
где
Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)
Тогда для неотрицательных целых
что соответствует известной формуле функции Бесселя первого рода для целых, неотрицательных
Для всех других решений — не существует разложения в ряд Tэйлора в нуле.
Пример 3. Числа Фибоначчи
Теперь рассмотрим, как можно решать рекуррентные уравнения с помощью эпсилон-преобразования.
Рассмотрим числа Фибоначчи, которые задаются следующим рекуррентным соотношением:
 ,
,
при этом, ,
,  , откуда следует, что
, откуда следует, что 
Это можно записать как
 или
или

Будем считать, что . Tогда получим
. Tогда получим
 ,
,
при этом и
и 
Шаг 1. (Обратное эпсилон-преобразование)
Выполняя обратное эпсилон-преобразование получим

при этом ,
, 
Шаг 2. (Решаем дифференциальное уравнение)
Мы можем решить это уравнение через преобразование Лапласа. Применим преобразование Лапласа. Получим

![$L(p)=\displaystyle{\frac{1}{(p^2+p-1)}}=\displaystyle{\frac{1}{(p_1-p_2)} \left[\frac{1}{p-p_1}-\frac{1}{p-p_2}\right]}$](https://habrastorage.org/getpro/habr/formulas/8a8/afc/d6c/8a8afcd6ca9f1375c85f52dfd4a1c9e1.svg) ,
,
где ,
,  — корни уравнения
— корни уравнения  и соответственно равны:
и соответственно равны:

 .
.
Но тогда .
.
Шаг 3. (Производим прямое эпсилон-преобразование)
Теперь запишем функцию, являющуюся эпсилон-образом .
.
Это будет

Соответственно, при получаем известную формулу
получаем известную формулу

Рассмотрим числа Фибоначчи, которые задаются следующим рекуррентным соотношением:
при этом,
Это можно записать как
Будем считать, что
при этом
Шаг 1. (Обратное эпсилон-преобразование)
Выполняя обратное эпсилон-преобразование получим
при этом
Шаг 2. (Решаем дифференциальное уравнение)
Мы можем решить это уравнение через преобразование Лапласа. Применим преобразование Лапласа. Получим
где
Но тогда
Шаг 3. (Производим прямое эпсилон-преобразование)
Теперь запишем функцию, являющуюся эпсилон-образом
Это будет
Соответственно, при
Свойства эпсилон-отображения при ε → 0
Обратное эпсилон-преобразование можно осуществить просто устремив
Это можно сформулировать более строго в виде теоремы, которую я приведу без доказательства.
Теорема
Пусть функции
Не аналитические функции
деление на икс в эпсилон-степени
До сих пор мы говорили только об аналитических (справа от нуля) функциях.
Можно ли «расширить» этот подход и на другие функции?
В качестве примера, попробуем найти эпсилон-образ для функции , где
, где  — натуральное число. Для этой функции нет разложения в ряд Тейлора в 0. Обозначим этот эпсилон-образ в соответствии с нашим подходом как
— натуральное число. Для этой функции нет разложения в ряд Тейлора в 0. Обозначим этот эпсилон-образ в соответствии с нашим подходом как  . Пусть
. Пусть

Тогда




Если , то получим, что
, то получим, что
 , таким образом получаем, что
, таким образом получаем, что
 для любого целого
для любого целого  (а не только для
(а не только для  )
)
Можно ли «расширить» этот подход и на другие функции?
В качестве примера, попробуем найти эпсилон-образ для функции
Тогда
Если
Эпсилон-произведение и дискретность пространства-времени
Все сказанное выше наводит на фундаментальный вопрос: a не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?
Рассмотрим, например, одномерное уравнение Шредингера:
Это уравнение предполагает непрерывность пространства-времени и возможность бесконечно малой величины
Чтобы не усложнять рассуждения, давайте рассмотрим случай когда
Но ведь
При этом
То есть при очень меленьком шаге времени (кванте времени)
Но тогда это значит, что мы не можем в действительности сказать, какое произведение является «истинным» («используется» природой) — наше обычное или эпсилон-произведение (с достаточно малым квантованием времени).
При этом в случае эпсилон-произведения (и соответственно эпсилон-уравнения Шредингера и его эпсилон-волнового решения), мы имеем очевидный плюс — квантование времени становится естественным, и мы не сталкиваемся с требованием бесконечной энергии. Фактически мы имеем все то же уравнение, с теми же решениями, но при этом естественным образом устраняем необходимость допущения непрерывности времени.
Замечание
Когда мы говорим о дискретности какой-либо измеряемой сущности, имеется ввиду то, что существуют четко отграниченные, неделимые элементы, из которых эта сущность состоит. Но когда мы говорим о дискретности пространства или о времени, то возможна также и иная интерпретация. Например, возможно, при достаточно малых значенияхили/и
уже нет смысла говорить о времени или о пространстве. Время и пространство, возможно, перестают существовать для этих величин. Таким образом мы получаем некие «размытое пятна» вместо точек, которые можно рассматривать как точки при
или/и
. В данном случае нельзя выделить кванты, но также нельзя говорить и о непрерывности. Но даже в этом случае мы также можем использовать описанный здесь эпсилон-подход, предполагая, что
— это те минимальные
или/и
, когда еще имеет смысл говорить о времени или/и пространстве (грубо говоря, это усредненный размер «пятна»).
Как проверить?
Итак, если время дискретно с «шагом»
Можно привести некоторые оценки, для понимания насколько сильно изменились бы наши представления о мире, если «истинным» было бы именно «эпсилон-умножение» (а не обычное умножение).
Вспомним, что
Тогда для
- частота будет отличаться от частоты синусоидального колебания
и будет равняться
- амплитуда будет расти как
Давайте грубо оценим, способны ли мы заметить это отличие?
Пример 1. Изменения за время жизни вселенной
Предположим, что наша временная дискретность сравнима с Планковским временем:
Время жизни вселенной:
Найдем для каких частот
Это значит, что для частот порядка 1 TГц (или для частиц с энергией
Пример 2. Изменения за секунду
Давайте оценим во сколько раз изменится амплитуда волновой функции частицы с ультравысокой энергией порядка
То есть за секунду амплитуда волновой функции такой частицы увеличится в 100 тысяч раз (порядок).
Выглядит существенным. Но как это обнаружить? Дело в том, что физический смысл имеет не сама волновая функция, а
Что говорит о том, что как раз величина, которая имеет физический смысл меняться не будет, и данный подход не позволит нам ответить на поставленный вопрос.
Ответы на вопросы из комментариев
Как было получено эпсилон-произведение
Разложим обычное произведение двух аналитических функций в ряд Тейлора (в точке 0).
В компактном виде это разложение можно записать как:

 — это краткое обозначение оператора
— это краткое обозначение оператора 
Заменим теперь в формуле обычного произведения операторы производной на операторы эпсилон-производной, экспоненту на
на  (как было показано, это и есть эпсилон-экспонента) и наши аналитические, непрерывные функции
(как было показано, это и есть эпсилон-экспонента) и наши аналитические, непрерывные функции  на решетчатые функции (из
на решетчатые функции (из  )
)  .
.
Это и будет нашим искомым эпсилон произведением, которое, как мы увидим удовлетворяет всем нашим требованиям:
 , где
, где  — единичный левый оператор для решетчатой функции:
— единичный левый оператор для решетчатой функции: 
Раскрыв скобки, мы получим следующий вид

что в компактном виде можно записать как:

Далее раскрывая скобки можно получить еще одну формулу:

где — биномиальный коэффициент Ньютона:
— биномиальный коэффициент Ньютона:  , (
, ( )
)
В компактном виде это разложение можно записать как:
Заменим теперь в формуле обычного произведения операторы производной на операторы эпсилон-производной, экспоненту
Это и будет нашим искомым эпсилон произведением, которое, как мы увидим удовлетворяет всем нашим требованиям:
Раскрыв скобки, мы получим следующий вид
что в компактном виде можно записать как:
Далее раскрывая скобки можно получить еще одну формулу:
где