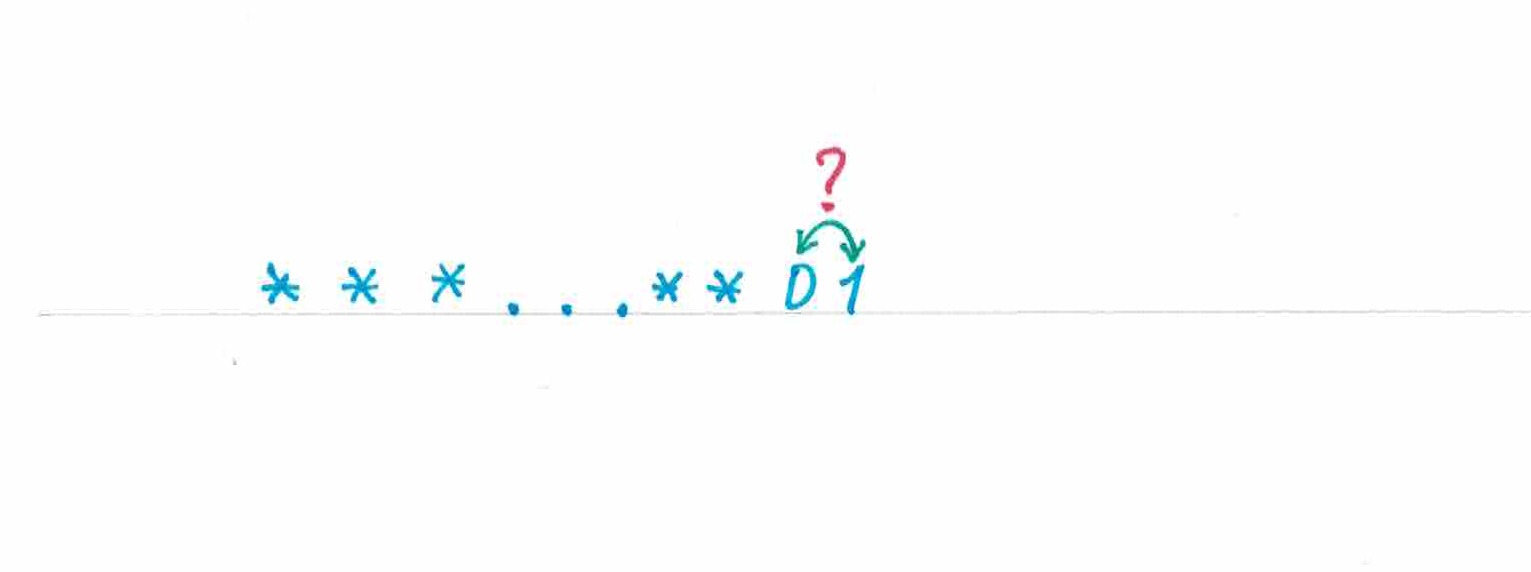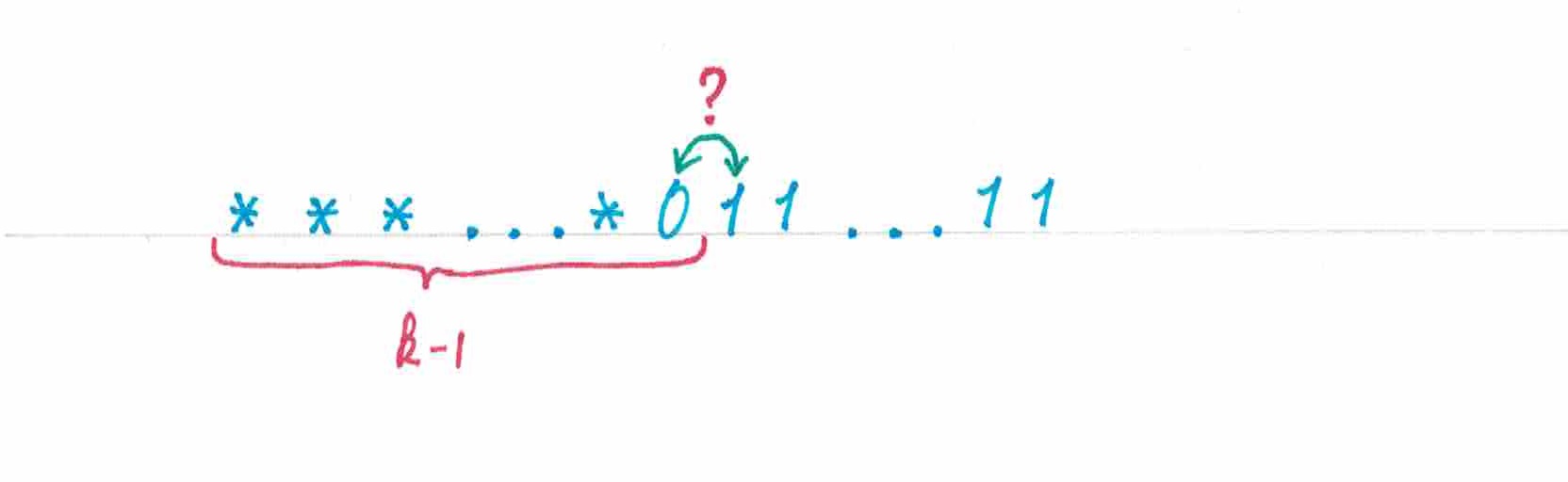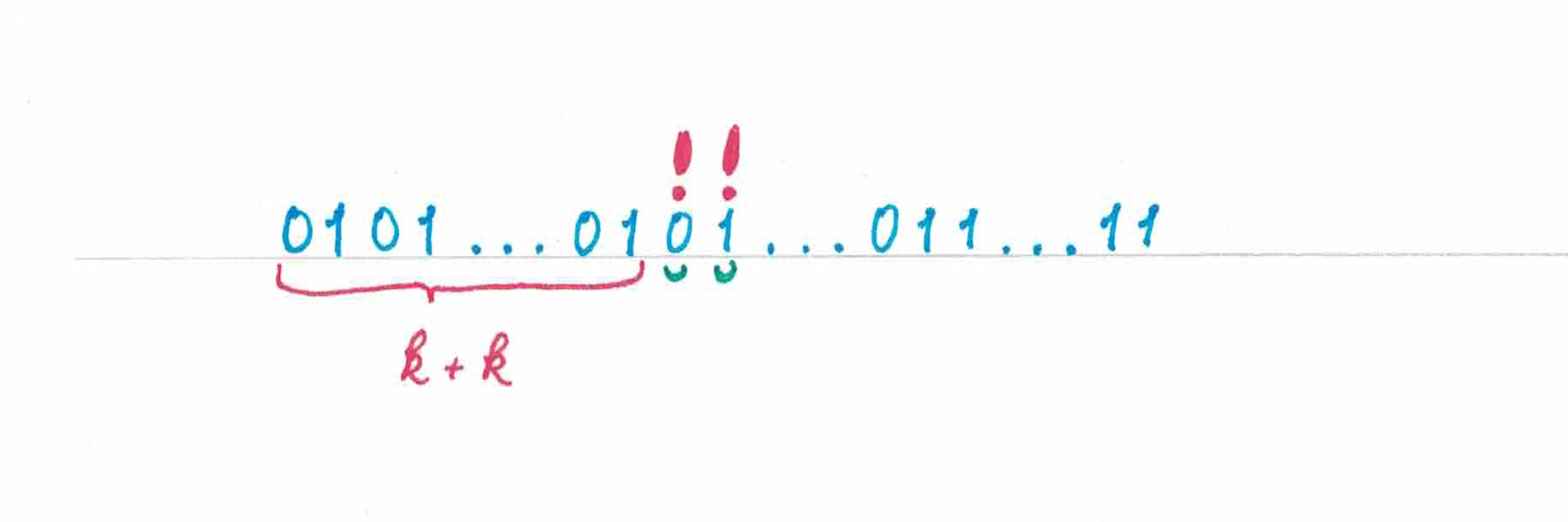(
Этот кашалот парит в воздухе целых 5 минут и поэтому решил, что его полет будет продолжаться вечно. рисунок: Tim Zarechny)
Философский вопрос с прикладными последствиями
Как вы думаете, если некоторая закономерность была подмечена в прошлом и непогрешимо выполнялась вплоть до настоящего момента, разумно ли в дальнейшем планировать свои действия так, как будто бы эта закономерность обязана выполняться и впредь? Озвученная только что проблема занимает одно из центральных мест в философии науки и тесно связана идеей адаптации. Ниже я постараюсь наметить ее решение, а заодно обсудить один очень интересный парадокс.
Собственно статья посвящена вот какому вопросу:
Пусть некое устройство печатает на бумажной ленте длинную последовательность из ноликов и единичек. Будем считать, что вам не известны ни принцип работы этого устройства, ни конечная длина воспроизводимой им последовательности. Представим, что от вас требуется как можно большее число раз угадать, какой символ будет напечатан следующим, и спустя некоторое время вы обнаруживаете, что среди напечатанных символов число единиц значимо больше числа нулей.
Должно ли это наблюдение заставить вас в будущем в качестве прогноза чаще называть «единицу»?
Если выяснится, что ответ на этот вопрос положительный, то мы получим крайне интересный прецедент, когда по сути статистические методы оказываются применимы к наблюдениям, природа которых не является вероятностной. Феномен подобного масштаба может даже стать поводом пересмотреть рамки современной математической статистики и границы ее приложения на практике.
Комфортное чтение статьи займет у Вас вечер или два, в процессе придется кое-что
вспомнить из университетской математикой 1-го года обучения. По всем непонятным вопросам Вы можете писать мне на почту или в комментарии.
Адаптация к случайным последовательностям
Случай, когда вероятность известна
Это исследование будет проще понять, если начать с задачи предсказания последовательностей, символы которых генерируются случайно. Пусть, имеется урна и вам известно, что в ней находятся

одинаковых на ощупь шаров, причем

из них черные, а оставшиеся

— белые. Пусть некто раз за разом повторяет такую процедуру: он достает из урны случайный шар, а затем печатает на ленте еще один символ. Если шар черный, то печатается «ноль», а если белый, то — «единица». После того, как символ напечатан, шар возвращается в урну. На все эти действия вы можете смотреть как на некую игру, состоящую из множества повторяющихся туров. Пусть ваша цель в игре — суметь как можно большее число раз угадать, какой появится на ленте следующим. Почти очевидно, что в описанных условиях наилучшей для вас стратегией будет все время называть одну и туже цифру: а именно ту, которая соответствует цвету большинства шаров в урне.
Действительно, угадать следующий символ на ленте

угадать цвет следующего шара. Математическое ожидание числа правильных предсказаний цвета за всю игру будет равно сумме математических ожиданий числа правильных предсказаний в каждом ее отдельном туре. Все туры проходят независимо друг от друга. Если перед тем, как будет вынут очередной шар, вы назовете «ноль», то по сути предскажите «черный» и математическое ожидание числа правильных предсказаний в этом туре окажется равным

, если отдадите предпочтение «единице», то ожидаемое число правильных предсказаний будет равно

. Таким образом, когда

, «выгоднее» голосовать за «ноль», а когда

, то — за «единицу».
При описанном только что алгоритме поведения математическое ожидание числа правильно предсказанных за всю игру символов будет равно

, где

выражает собой
дисбаланс вероятности появления «нуля» и «единицы».
Обобщение на случай с неизвестной вероятностью
Пусть снова вы имеете дело с той же самой игрой, но теперь информация о том, каково число черных и белых шаров в урне держится от вас в секрете. Как и в прошлый раз нас будет интересовать вопрос: «Какова средняя доля шаров, окраску которых можно предугадать, если действовать оптимально?»
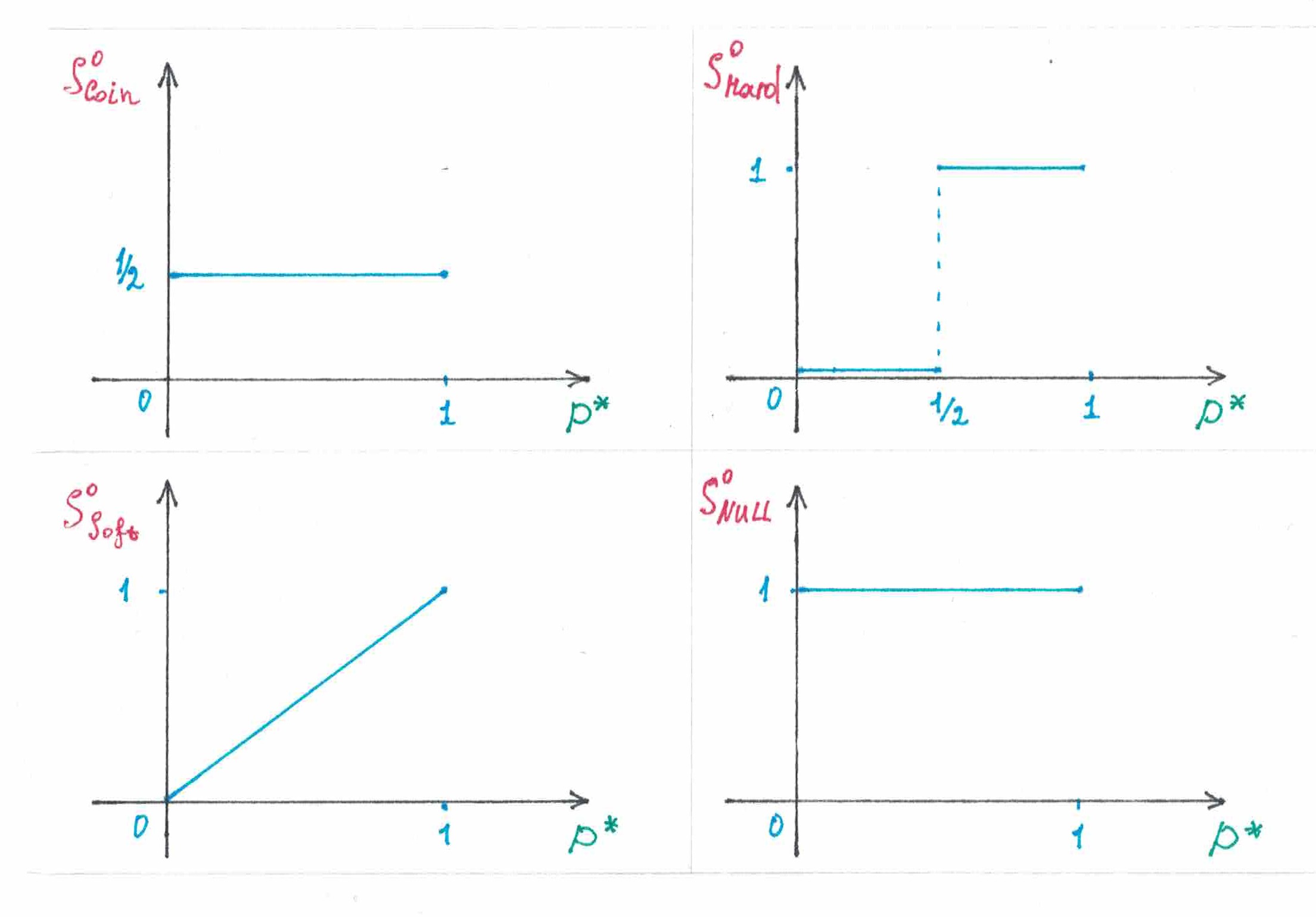
Перво-наперво здесь нужно сказать об одной крайне простой, но замечательной стратегии (я назову ее

), позволяющей «в среднем» угадывать ровно половину символов вообще в любой бинарной последовательности, не важно: случайной, или нет. По правилам

перед тем как сделать очередной прогноз вы должны бросить монетку и, если выпала решка, предсказать «единицу», а если орел — то «ноль». Если действовать таким образом, то математическое ожидание числа угаданных символов будет ровно

вне зависимости от того, какая именно последовательность окажется в итоге напечатанной на ленте.
Хорошо, предсказывать

всех символов мы способны с помощью

, а можно ли предсказывать больше?
Если бы мы знали наперед, какое из неравенств верно:

, или

, то с легкостью воспользовались бы результатами предыдущей задачи и угадали бы

плюс

от всех символов, однако по условию мы не можем получить такую информацию извне. С другой стороны, если в игре уже минуло какое-то количество туров, то соотношении между

и

можно попробовать оценить из наблюдений. Понятно, что при

среди первых

напечатанных символов с большей вероятностью будут преобладать «нули», а при

— с большей вероятностью будут преобладать «единицы».
Пожалуй, самую простую стратегию, основанную на статистической оценке

и

, можно описать следующим планом действий:
в первом туре с помощью монетки выбрать случайный символ,
в начале каждого следующего тура сосчитать, сколько раз среди уже напечатанных символов встречается «единица», сколько раз встречается «ноль», и в качестве прогноза назвать тот символ, который на момент наблюдений встречается чаще.
Если вдруг «ноль» и единица" в минувших турах успели появится одинаковое число раз, то в качестве прогноза следует назвать тот же символ, что предсказывался в предыдущем туре. По причинам, которые станут очевидными позже, мы будем называть эту стратегию

.
Насколько эффективна

по сравнению с другими возможными стратегиями, насколько математическое ожидание доли правильно предсказанных ею символов больше

? Чуть позже мы дадим на эти эти вопросы исчерпывающий ответ, а сейчас ограничимся поверхностными оценками.
Сперва отметим, что для любой стратегии, действующей в условиях, когда

и

неизвестны, математическое ожидание количества правильно предсказанных ею символов не может превзойти результата лучшей стратегии для ситуации с известными

и

(дополнительная информация никогда не бывает лишней). Лучшая из стратегий последнего типа была найдена нами выше и ее результат:

, откуда мы получаем верхнюю оценка для

.
Итак, эффективность применения

заключена где-то между

и

, и в действительности возможны случаи, когда достигается каждая из границ. Например, если последовательность состоит ровно из одного элемента, то согласно правилам

, шансы угадать этот элемент составят ровно

(прогноз определяется с помощью монетки). С другой стороны, когда

не равно

и при этом в последовательности уже напечатано

элементов, вероятность того, что в этот момент или когда-либо позже количество вхождений в нее менее вероятного символа превысит число вхождений более вероятного, с ростом

очень быстро стремиться к нулю (см. несимметричное броуновское движение). Таким образом, если случайная последовательность достаточно длинная, то только для относительно небольшой доли ее элементов в качестве прогноза

выдаст менее вероятный символ, а значит эффективность

в такой ситуации окажется близкой к

. Кстати, последнее свойство

позволяет нам говорить о ней как об асимптотически оптимальной стратегии угадывания вероятностных последовательностей.
Адаптация к не(обязательно)случайным последовательностям. Поверхностный анализ
Неочевидность подхода
Давайте подумаем, почему адаптивные стратегии угадывания символов сработали на случайных последовательностях?
Основная причина их успешного применения кроется в том, что свойство случайности имеет одинаковую тенденцию проявлять себя на любом участке последовательности. Если вероятность появления символов изначально неизвестна, то ее удается легко восстановить из наблюдений.
Теперь перед вами должна раскрыться вся неочевидность попытки применить адаптивные стратегии к отгадыванию элементов в неслучайных, скажем, рукотворных последовательностях. Действительно, любая закономерность на любом сколь угодно длинном начальном участке рукотворной последовательности может быть в любой момент прервана или даже обращена в контрзакономерность.
Разумеется для отгадывания неслучайных последовательностей по прежнему работает «трюк с монеткой»: делая предсказания «нуля» на «орел» и «единицы» на «решку», вы гарантируете себе математическое ожидание величиною в

угаданных символов. Можно ли угадать больше?
Частотный дисбаланс
По отношению к неслучайным последовательностям тоже можно ввести понятие дисбаланса, но только не вероятностного, а частотного. Если некоторая последовательность состоит из

символов:

«нулей» и

«единиц», то по определению ее частотный дисбаланс

есть

. Новое определение дисбаланса в некотором смысле даже «обратно совместимо» со старым, так как для длинных случайных последовательностей с большой вероятностью

,

, а значит

.
Как вы уже знаете, наличие дисбаланса между вероятностями появления «нуля» и «единицы» в случайной последовательности позволяет правильно угадать в среднем больше половины ее элементов. Раз мы ввели понятие частотного дисбаланса, то совершенно естественно теперь задать вопрос:
«Позволяет ли наличие частотного дисбаланса угадать в среднем больше половины элементов в неизвестной, но не обязательно случайной последовательности, если к тому же заранее не известно, каких символов в ней больше: „нулей“ или „единиц“?»
Насколько хороша  ?
?
Поиски ответа мы начнем с того, что попробуем испытать уже использовавшуюся нами раннее стратегию

. Эта стратегия неплохо себя показала на случайных последовательностях и даже оказалась на них асимптотически оптимальной.
Итак, предположим, что на ленте печатается длинная последовательность ноликов и единичек с частотным дисбалансом

.
Как много ее элементов удастся предугадать с помощью

?
Поскольку теперь у нас нет «мифического» случайного порядка символов, нет действия Закона больших чисел или других предельных законов теории вероятностей, то количество отгаданных символов будет существенно зависеть от конкретного вида последовательности. Рассмотрим несколько примеров.
рис 1.
В первом примере

и все

«нулей» последовательности стоят строго перед ее

«единицами» (рис1). Для такой последовательности

правильно предскажет все «нули», кроме быть может первого (вероятность предсказать правильно первый «ноль» равна 50%-там), и даст ошибочный прогноз для каждой «единицы». Таким образом, математическое ожидание доли правильно предсказанных символов составит

.
Что ж, это весьма неплохой результат. Я предлагаю вам самостоятельно проверьте, что ровно с таким же результатом

угадает и «перевернутую» последовательность, у которой

«единиц» стоят в начале, а

«нулей» — за «единицами» в конце.
рис 2.
Рассмотрим теперь куда более интересный пример «парно-пульсирующей» последовательности (рис 2). Первый ее элемент — «единица», далее следует «пульсирующий» отрезок, на котором

нулей парами чередуются с

единицами, а вслед за ним — «гомогенный» отрезок, стоящий из идущих друг за дружкой

единиц. Давайте проследим, какие прогнозы для элементов этой последовательности будет делать

.
- Первый прогноз будет не то нулем, не то единицей — в общем, он нам не особо интересен.
- Далее
 наблюдает, что единственный напечатанный символ — это «единица», следовательно прогноз второго элемента — это «единица», тем самым
наблюдает, что единственный напечатанный символ — это «единица», следовательно прогноз второго элемента — это «единица», тем самым  ошибется в своем втором предсказании.
ошибется в своем втором предсказании.
- Смотрим на третий прогноз: в этот момент на ленте напечатаны один «ноль» и одна «единица» — между числом употребления двух символов наблюдается паритет, а значит
 должна повторить свой предыдущий прогноз, то есть назвать «единицу» и ошибиться еще раз.
должна повторить свой предыдущий прогноз, то есть назвать «единицу» и ошибиться еще раз.
- На момент четвертого прогноза уже больше напечатано «нулей», поэтому
 предскажет «ноль» и снова ошибется.
предскажет «ноль» и снова ошибется.
Легко видеть, что кроме быть может только первого элемента, все предсказания

на «пульсирующем» участке будут ошибочными. К моменту, когда этот участок закончится, на ленте будет напечатано

«нулей» и

«единица», поэтому оставшиеся

единицу

предскажет правильно. Объединяя эти факты вместе, мы находим, что доля символов последовательности, которые угадает

, будет равна

Конечно, когда дисбаланс парно-пульсирующей последовательности близок к

(то есть, когда ее «гомогенный» участок занимает почти всю ее длину),

близко к единице и предсказания

работают просто великолепно. Однако в случае, когда дисбаланс подобных последовательностей близок к нулю, результаты предсказаний

оказывается даже хуже, чем у стратегии с монеткой. Более того, если вся последовательность состоит из попарно чередующихся «нулей» и «единиц», то

вообще не угадывает ни одного символа, за исключением быть может первого.
Итак, на неслучайных последовательностях

способна работать очень плохо, настолько плохо, что возможны ситуации, когда математическое ожидание доли правильно угаданных символов будет практически равно нулю. Приведенный выше пример с пульсирующей последовательностью во многом объясняет, почему так может происходить.
Все дело в том, что

слишком резко реагирует на любые изменения частот напечатанных на ленте символов, когда эти частоты колеблются вокруг

. Чрезмерная реакция на изменения позволила нам с помощью специального вида последовательности манипулировать предсказаниями

и в конце концов легко ее «обмануть». Можно ли как-то исправить

, сделав эту стратегию более устойчивой к манипуляциям и «обману»?
Суперпозиция предположений
Когда среди напечатанных символов вы наблюдаете одни «единицы», совершенно «логично» предположить, что следующий символ тоже должен быть «единицей», когда на ленте сплошь одни «нули» — «нулем». Однако как подсказывает нам неудача со стратегией

, если и тех, и других символов обоюдно много, то что в качестве предсказания стоило бы выбрать что-то «посередине». Но как это сделать, ведь по условию наше предсказание обязательно быть чем-то одним: либо нулем, либо единицей?
Эта задача похожа на выбор смешанной стратегии в теории игр и решается она следующим образом: для заданных весов

и

нужно поставить любой случайный эксперимент, о котором известно, что он завершается событием

с вероятностью

и противоположным событием

с вероятностью

. Если в результате произошло событие

, то в качестве предсказания выбирается «ноль», а если

— то «единица». Я не владею квантовой механикой, но предполагаю, что физики назвали бы такое предсказание взвешенной суперпозицией «нуля» с весом

и «единицы» с весом

.
Суперпозиция предсказаний на самом деле уже использовалась нами в стратегии

: там «ноль» и «единица» входили в суперпозицию с весами равными

. Более того, даже на детерминистические предсказания стратегии

можно смотреть как на взвешенные. В такой интерпретации каждый из двух возможных символов

предсказывает с вероятностью ноль, когда его частота в уже напечатанной части последовательности меньше

и с вероятностью единица, когда эта частота превышает

.
рис 3
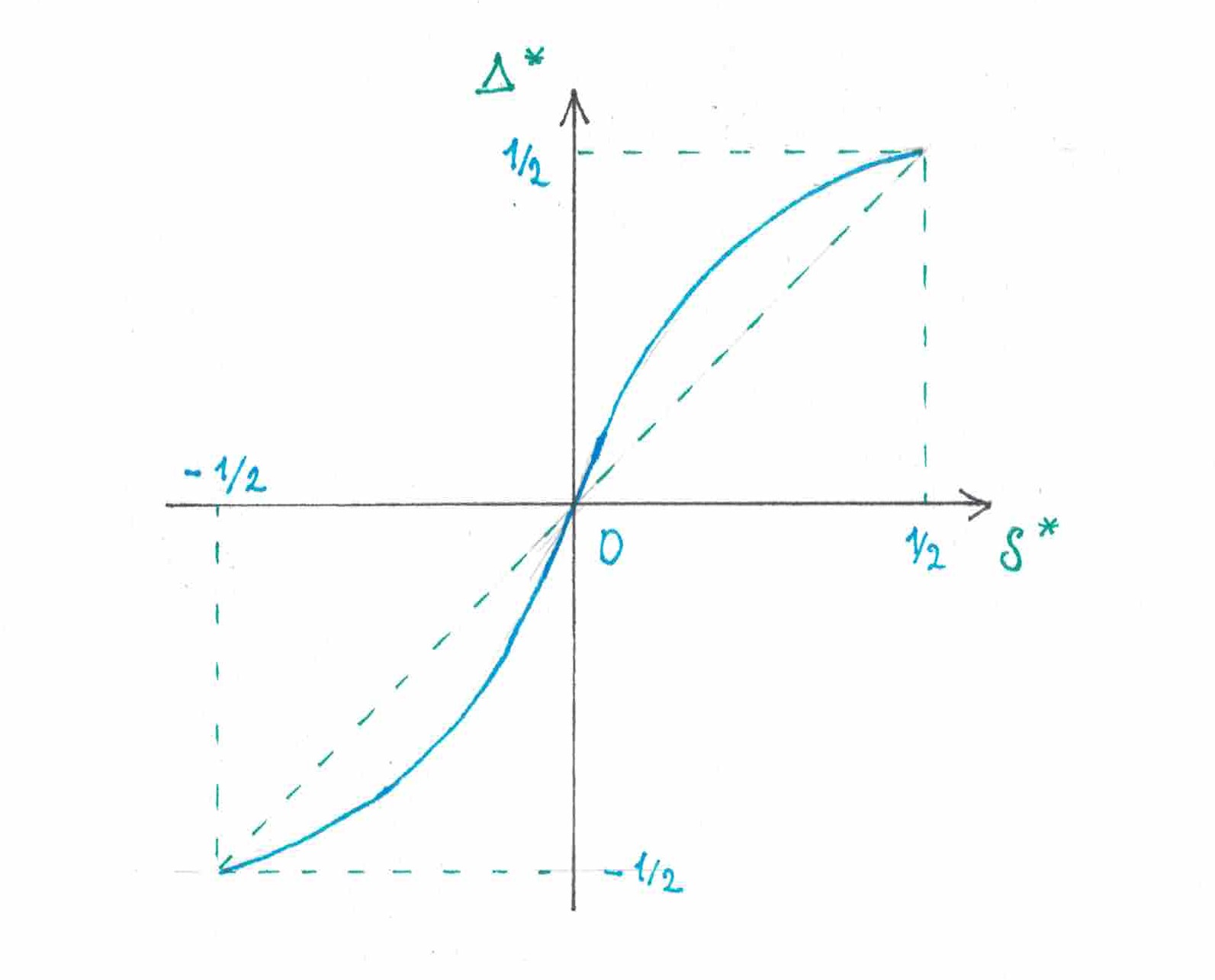
Если вероятностный вес символа в предсказаниях, даваемых

, рассматривать как функцию его наблюдаемой частоты, то эта функция будет изменяется не непрерывно. Как видно из рисунка 3, она испытывает резкий скачок в точке

. Наличие этого скачка как раз-таки и заставляет

менять свои предсказания на диаметрально противоположные каждый раз, когда частота символов меняет свое положение относительно

.
А что будет, если для предсказания мы воспользуемся стратегией, у которой вероятностные веса обоих символов являются непрерывными функциями от их наблюдаемых частот?
Непрерывная стратегия 
Пожалуй, самый простой способ заставить вероятностный вес символа непрерывно зависеть от его наблюдаемой частоты — это положить их равными друг другу. Стратегию, которая при наблюдаемых частотах «нуля» —

и единицы —

, предсказывает «ноль» с вероятностью

и «единицу» с вероятностью

, договоримся называть

. Такое название выбрано по аналогии с названием популярной в машинном обучении функцией

, которая, также как и

, в своей области применения является «гладким» аналогом операции взятия максимума.
В чем заключается смысл стратегии

? Если вы видите, что в напечатанной последовательности 10% «нулей» и 90% единиц, то ваше предсказание должно с вероятностью 10% стать «нулем» и с вероятностью 90% — оказаться единицей. Если «нулей» на ленте 90%, а единиц 10%, то все должно быть ровно наоборот. Если же единиц и нулей напечатано оказалось примерно поровну, то и предсказаны они должны быть примерно с одинаковыми вероятностями. Функции зависимости вероятностного веса символа от его наблюдаемой частоты у

линейны, вы их можете рассмотреть на рисунке 4.
рис 4
Насколько хорошо

приспосабливается к дисбалансу, насколько удачно у нее получается угадывать символы? Чтобы «прощупать» эти вопросы, давайте возьмем несколько простых последовательностей и попробуем запустить алгоритм

на них.
Эффективность  в простейших случаях
в простейших случаях
В качестве первого примера рассмотрим цепочку, составленную из двух гомогенных отрезков: последовательно расположенных

нулей и

единиц (рис 5). Я буду предполагать, что эта цепочка достаточно длинная, чтобы была возможность пренебречь «особенностью» угадывания первого символа.
рис 5
Все время, пока на ленте печататься только нули, их частота остается равной

, поэтому

угадает их все (за исключением быть может первого). Затем начнут появляться единицы. Поначалу доля «единиц» среди присутствующих на ленте символов будет мала, поэтому и предсказывать «единицу»

будет редко. Однако в месте с тем, как число напечатанных «единиц» будет расти, будет расти и вероятность следующую из них предсказать правильно.
Чтобы провести количественные оценки, рассмотрим две альтернативы:
- в итоговой последовательности больше нулей
- в итоговой последовательности количество единиц больше или равно количеству нулей
Если верна первая альтернатива, то уже только успешное предсказание всех (за исключением
может быть первого) нулей позволяет

правильно угадать больше половины всех символов.
Предположим теперь, что верна вторая альтернатива. Сможет ли в этой ситуации

превзойти стратегию угадывания при помощи монетки?
Чтобы ответить на этот вопрос, мысленно разобьем последовательность на два отрезка: первый из них должен включать в себя

нулей и

единиц, а второй — все оставшиеся

единицы (рис 6).
рис 6
На первом отрезке

угадает все нули и еще какое-то число единиц, таким образом предсказанными правильно «в среднем» окажутся больше половины его символов. К моменту когда начнет печататься второй отрезок, количество единиц на ленте уже успеет сравняться с количеством нулей, а значит каждый следующий прогноз с вероятностью не меньшей 50% будет правильно предсказывать единицу. Математическое ожидание числа угаданных символов на втором отрезке также оказывается не меньше половины его длинны. Объединяя результата по двум отрезкам, мы можем заключит, что «в среднем» на подобных последовательностях у

в любом случае получится угадать не меньше половины их элементов.
Эффективность  на пульсирующих последовательностях. Формулы
на пульсирующих последовательностях. Формулы
Как вы помните, стратегия

перестала хорошо работать, когда мы применили ее к последовательности, у которой которой роль наиболее распространённого символа в процессе печатанья то и дело переходила от «единицы» к «нулю» и обратно. Давайте посмотрим, каким образом теперь уже

будет вести себя в подобной ситуации.
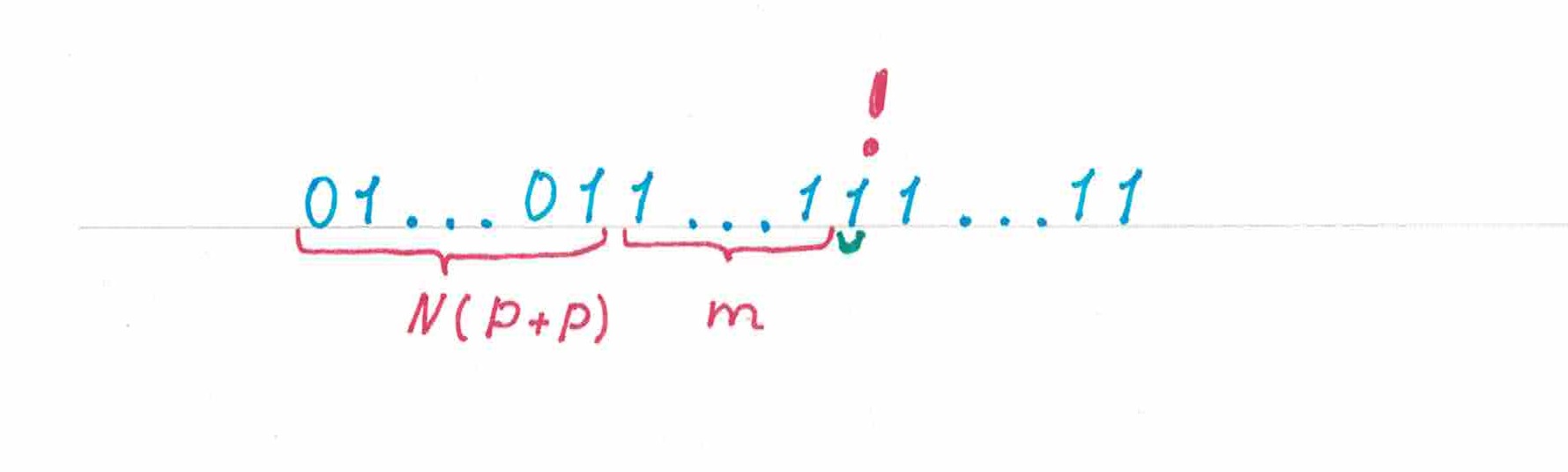
Для эксперимента возьмем последовательность, составленную из двух участков: стоящего спереди участка «пульсации», где все

«нулей» последовательности строго чередуются с ее первыми

«единицами», и идущего за ним «гомогенного» отрезка, заполненного оставшимися

«единицами» (рис 7). Похожие последовательности мы будем называть
пульсирующим префиксного типа (в то время как последовательности, у которых участок чередования символов стоит в конце — именовать
пульсирующими суфиксного типа).
рис 7
Предсказания

будут следующими:
- Первый элемент будет угадываться с помощью монетки и поэтому он нам не особо интересен.
- В момент предсказания второго элемента среди напечатанных на ленте символов будет 100% нулей, поэтому
 даст прогноз нуля и 100% ошибется.
даст прогноз нуля и 100% ошибется.
- На момент предсказания третьего символа нулей и единиц на ленте поровну, значит с вероятностью 50% сделанный прогноз окажется верным
- Пусть уже напечатано
 «нулей» и
«нулей» и  «единиц» (рис 8), посмотрим с какой вероятностью алгоритм угадает очередной «ноль» и очередную «единицу».
«единиц» (рис 8), посмотрим с какой вероятностью алгоритм угадает очередной «ноль» и очередную «единицу».
рис 8
В момент, когда должен появится «ноль» символов обоих типов на ленте поровну, значит  угадает его с вероятностью
угадает его с вероятностью  . На следующем шаге «нулей» на ленте станет на один больше и вероятность угадать «единицу» будет равна
. На следующем шаге «нулей» на ленте станет на один больше и вероятность угадать «единицу» будет равна 
Отсюда следует, что математическое ожидание числа угаданных символов последовательности на участке их чередования есть:

Предполагая, что  достаточно велико, мы с большой относительной точностью можем заменить сумму интегралом:
достаточно велико, мы с большой относительной точностью можем заменить сумму интегралом:

Таким образом среднее число символов, угаданных  на отрезке «пульсации», составит:
на отрезке «пульсации», составит:

, заменив одно из вхождений  на
на  , то же самое можно выразить и в другой форме:
, то же самое можно выразить и в другой форме:

- Пусть уже напечатан весь отрезок «пульсации» и еще
 следующих за ним «единиц» «гомогенного» участка (рис 9).
следующих за ним «единиц» «гомогенного» участка (рис 9).
рис 9
В этот самый момент на ленте будут находятся  «нулей» и
«нулей» и  «единица», а значит вероятность того, что предсказание, сделанное
«единица», а значит вероятность того, что предсказание, сделанное  , окажется единицей, есть
, окажется единицей, есть

Отсюда находим, что из  «единиц» «гомогенного» участка в среднем правильно предсказанными окажутся:
«единиц» «гомогенного» участка в среднем правильно предсказанными окажутся:

Чтобы дать асимптотическую оценку этой формуле, рассмотрим два случая:

 мало по сравнению с
мало по сравнению с  , что по сути эквивалентно условию
, что по сути эквивалентно условию  или тому, что
или тому, что 

 и
и  являются величинами одного порядка или даже
являются величинами одного порядка или даже  много больше
много больше  . То же самое может быть выражено требованием, чтобы дисбаланс
. То же самое может быть выражено требованием, чтобы дисбаланс  был соизмерим с единицей.
был соизмерим с единицей.
Если верно  , то мы можем переписать:
, то мы можем переписать:

далее:

в свою очередь стоящее справа в  выражение является суммой арифметической прогрессии, вычислить которую не составит большого труда:
выражение является суммой арифметической прогрессии, вычислить которую не составит большого труда:

Подставив найденное нами выражения для суммы в  и используя тот факт, что
и используя тот факт, что  , мы получим:
, мы получим:

Таким образом, при больших  и малых значениях
и малых значениях  среди
среди  «единиц» «гомогенного» участка правильно предсказанными в среднем окажутся примерно:
«единиц» «гомогенного» участка правильно предсказанными в среднем окажутся примерно:

Перейдем теперь к случаю  . Поскольку теперь предполагается, что диапазон изменения
. Поскольку теперь предполагается, что диапазон изменения  велик, то входящую в
велик, то входящую в  сумму с хорошей точностью можно заменить интегралом:
сумму с хорошей точностью можно заменить интегралом:

В свою очередь:

Подставив найденное выражение в  , мы получаем, что когда
, мы получаем, что когда  соизмерима с единицей, число угаданных символов «гомогенного» отрезка асимптотически может быть представлено как:
соизмерима с единицей, число угаданных символов «гомогенного» отрезка асимптотически может быть представлено как:

или в эквивалентной форме:

Эффективность  на пульсирующих последовательностях. Выводы
на пульсирующих последовательностях. Выводы
После того, как мы нашли среднюю результативность

на отдельных участках, давайте подсчитаем, сколько символов будет ею угадано во всей последовательности.
Если

, то нам необходимо сложить

и

:

а если

соизмерима с единицей, — то

и

:

Таким образом для малых

средняя доля угаданных символов выражается формулой

:

а если

соизмерима с единицей, то формулой

:

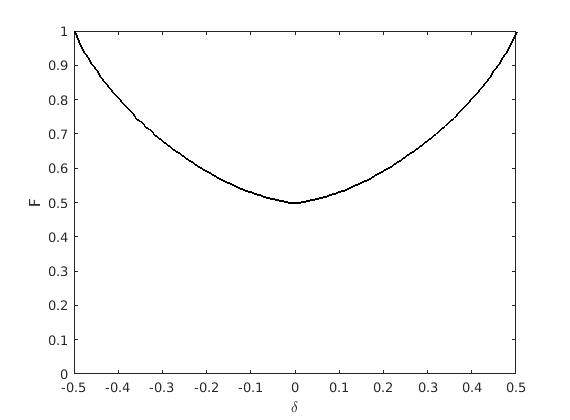
Какие мы можем сделать выводы, глядя на эти формулы?
Во первых стоит обратить внимание на присутствующее в обеих формулах слагаемое

Как вы уже наверное догадались, с ростом

его значение довольно быстро сходится к нулю и применительно к длинным последовательностям этим членом можно пренебречь. Если так, то формула

показывает, что даже при небольшой величине дисбаланса между «нулями» и «единицами»

угадывает в среднем примерно на

больше символов, чем если бы эти символы предсказывались с помощью бросания монетки. В свою очередь, если дисбаланс велик, то из формулы

следует, что асимптотически доля угаданных символов задается функцией

На на рисунке 10 изображен график этой функции, из которого видно, что и при соизмеримых с единицей

в пульсирующих последовательностях

в среднем угадывает все равно больше символов, чем делает это стратегия с подбрасыванием монетки.
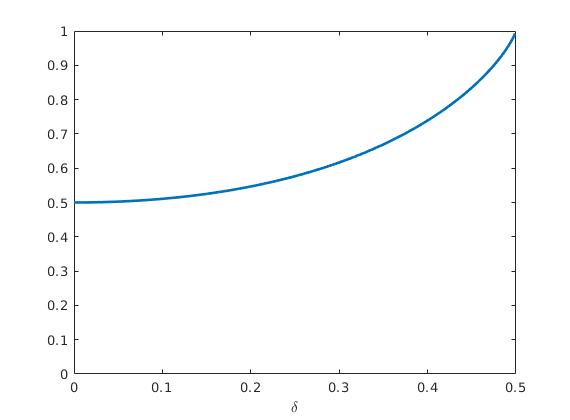
рис 10
Хорошо, похоже нам удалось показать, что

угадывает в среднем больше половины символов, если последовательность имеет по ним дисбаланс и относится к одному из двух специальных типов. Однако в рамках настоящего исследования куда более важным является другой вопрос: способна ли

угадывать в среднем больше половины символов в
любой последовательности при том единственном условии, что эта последовательность составлена из значимо различного количества «нулей» и «единиц». Мы сможем дать на него ответ, если для любых

,

и

среди всех последовательностей с

«нулями»

«единицами» найдем те, которые

получается предсказывать хуже всего.
Эффективность  в наихудшем для нее сценарии
в наихудшем для нее сценарии
Пусть у нас имеются

«нулей» и

«единиц». В каком порядке их нужно расставить на ленте, чтобы в получившейся последовательности математическое ожидание числа угаданных

элементов оказалось наименьшим?
Как вы наверное догадались, эту задачу было бы трудно решить прямым перебором, ведь даже для конкретных

и

, когда те одновременно велики, возможных способов расставить символы будет попросту астрономически много. Вместо метода грубой силы попробуем пойти другим путем и попытаемся понять, какими свойствами должна обладать последовательность, чтобы ее предсказуемость по отношению к

уже нельзя было ухудшить.
Собственно идея нашего подхода будет следующей: пусть имеется некоторая последовательность с характерным для нее порядком «нулей» и «единиц», выберем в этом порядке какой-нибудь «ноль», какую-нибудь «единицу», а затем поменяем их местами. Если предсказуемость изначальной последовательности по отношению к

уже была минимальной, то произведенная нами транспозиция не сможет сделать ее меньше.
Обратное утверждение, вообще говоря, не верно, однако если среди всех последовательностей, составленных из

«нулей» и

«единиц», подобным свойством будет обладать всего одна, то именно она и будет решением нашей задачи.
Предположим, что

и наша последовательность оканчивается парой:

. В каком из случаев

угадает больше элементов: если мы оставим все как есть, или поменяем два последних символа местами?
рис 11
Очевидно, что предполагаемая перестановка никак не повлияет на среднее число символов, которые

угадает среди первых

элементов, и нам остается только посчитать, как будет различается эффективность предсказаний двух последних символов до и после их перестановки.
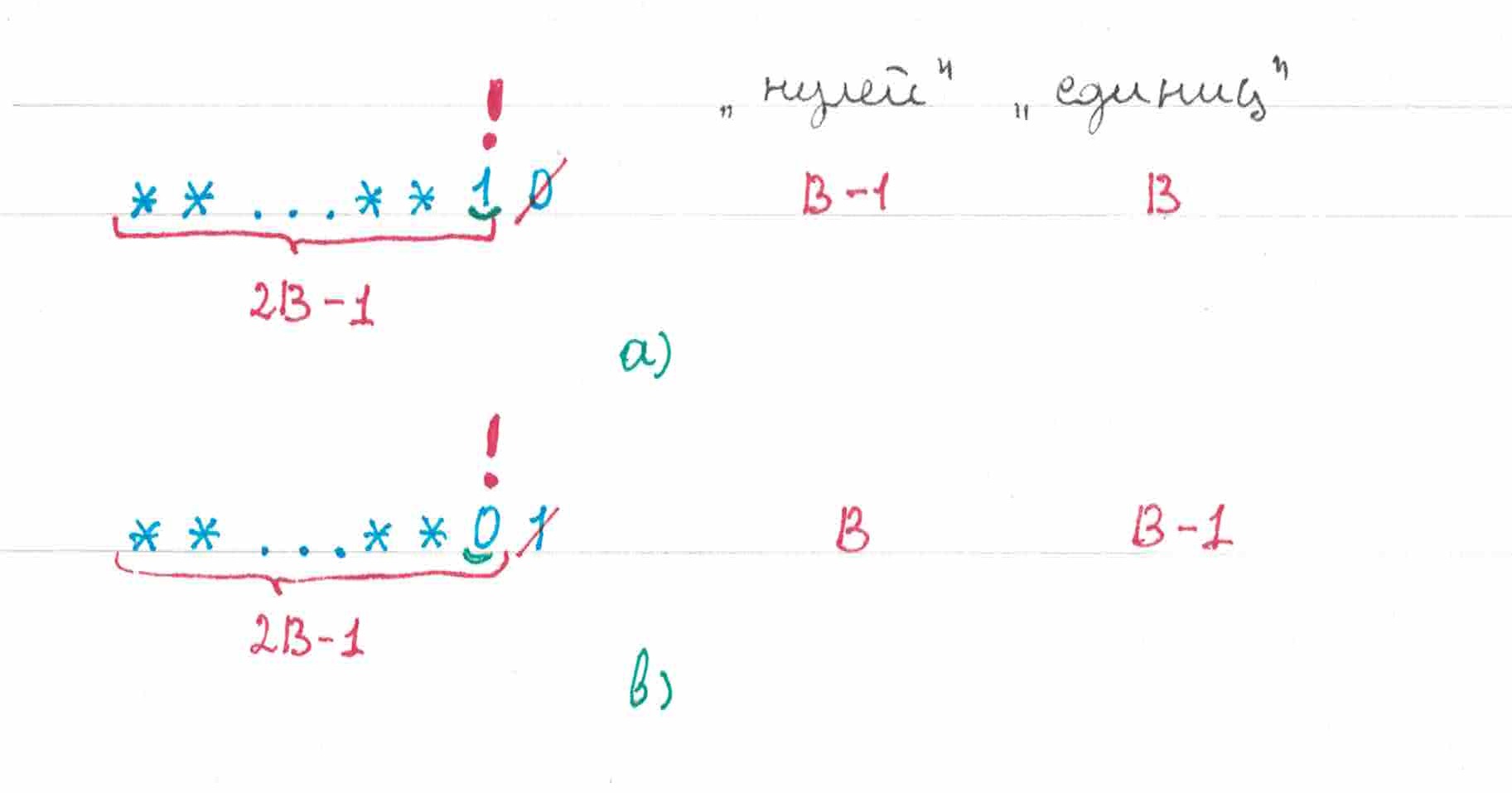
В изначальном порядке стоящий на предпоследнем месте «ноль»

правильно предскажет с вероятностью

, а стоящую последнем месте единицу — с вероятностью

, таким образом среднее число угаданных символов на этих двух позициях будет равно:

Если выполнить транспозицию, то шансы угадать ноль станут равными

, а шансы угадать единицу —

, поэтому формула для среднего числа правильно предсказанных символов примет вид:

Из этих двух формул видно, что

предсказывает хуже тот вариант последовательности, в конце которой стоит более распространенный в ней символ. Согласно нашим допущениям

, а значит этим символом должен быть «ноль».
Итак, если предсказуемость последовательности по отношению к

минимальна и

, то она не может оканчиваться единственной «единицей», перед которой стоит «ноль». Давайте проверим, может ли она заканчиваться несколькими единицами, стоящими подряд.
рис 12
Пусть дана последовательность (рис 12), у которой на

-ой позиции стоит «ноль», на

-ой и последующих позициях — «единицы» и соответственно на первых

-ух позиция в ее начале как-то размещены остальные

«нулей» и

«единиц». Если мы стремимся к тому, чтобы

в среднем угадала как можно меньше элементов, должны ли мы оставить в этой последовательности все как есть, или нам следует самый правый «ноль», находящийся на

-ой позиции, и соседнюю с ним «единицу» на

-ой поменять местами?
Здесь стоит сделать маленькое отступление и указать на одну важную особенность в алгоритме работы

: вероятностные веса, с которыми выбираются «ноль» и «единица» для предсказания

-го элемента, зависят только от соотношения между их числом среди первых

-го символов последовательности (на ее начальном отрезке длины

), и совершенно не зависят от того порядка, в котором эти символы там расположены. Если в конкретной последовательности поменять местами произвольное количество символов среди первых ее

элементов, то такая перестановка никак не скажется на эффективности, с которой

будет угадывать элементы с номерами от

(включительно) до

(включительно). Отсюда, кстати, следует простая, но замечательная
Лемма 1:
Если какая-то последовательность обладает минимальной по отношению к  предсказуемостью, то и любой ее начальный отрезок также является последовательностью, наименее предсказуемой для
предсказуемостью, то и любой ее начальный отрезок также является последовательностью, наименее предсказуемой для 
.
(Действительно, пусть

— бинарная последовательность длины

, обладающая минимальной по отношению к

предсказуемостью, а

— какое-нибудь число, меньшее

. Если бы предсказуемость последовательности первых

элементов

по отношению к

не была минимальной, то их можно было бы расставить в другом порядке, сделав ее (предсказуемость) таковой. С другой стороны произведенная перестановка нисколько бы не повлияла на величину математического ожидания числа тех элементов, которые

должна угадать на отрезке
![$[L+1, N]$](https://habrastorage.org/getpro/habr/formulas/6de/027/deb/6de027deb9c85faf5f4840e714326c9c.svg)
, а значит предсказуемость всей видоизмененной последовательности оказалась бы меньше, чем у

. Полученное противоречие как раз и доказывает Лемму

.)
Вернемся однако к вопросу, который был задан выше: пусть в бинарной последовательности
количество «нулей» в целом больше числа «единиц», уменьшится ли ее предсказуемость, если самый правый «ноль» в ней поменять местами со состоящей справа от него «единицей»?
На самом деле мы можем свести эту задачу к уже решенной. Для этого мысленно вычеркнем из
последовательности рисунка 12 все подряд стоящие в конце единицы, за исключением самой левой из них. В результате получится «укороченная» последовательность, которая заканчивается парой

. Поскольку в оригинальной последовательности «единиц» было меньше «нулей», то это же неравенство сохранится между ними и в ее «урезанной» версии. Таким образом мы оказываемся в условиях предыдущей задачи и можем утверждать, что предсказуемость последовательности уменьшится, если стоящие на конце ноль и единицу поменять местами.
После того, как самый правый «ноль» будет перемещен на соседнюю позицию справа, мы снова получим последовательность, заканчивающуюся некоторым количеством подряд идущих единиц, перед которыми стоит этот самый «ноль». Следовательно, если мы стремимся уменьшить предсказуемость последовательности, то снова можем переместить его вправо еще на одну позицию и еще на одну и так до тех пор, пока он не окажется в самом конце последовательности. Этими рассуждениями мы только что доказали вторую необходимую нам
Лемма 2:
Если последовательность обладает наименьшей по отношению к  предсказуемостью, то она не может заканчиваться менее распространенным в ней символом.
предсказуемостью, то она не может заканчиваться менее распространенным в ней символом.
Имея в своем распоряжении леммы

и

, уже совсем не трудно выяснить, в каким видом должна обладать бинарная последовательность

, чтобы ее предсказуемость относительно

была минимальной.
Пусть буква

— обозначает число «нулей», которые включает в себя

, а буква

— число содержащихся в ней «единиц». Поскольку относительно «единиц» и «нулей» задача полностью симметрична, то без ограничения общности мы можем предполагать, что

.
Разберем сначала случай, когда неравенство между

и

является строгим. Поскольку при этом «нулей» в

будет строго больше, чем единиц, то согласно лемме

на ее конце должен стоять «ноль» (рис 13a). Мысленно вычеркнем этот ноль. Оставшаяся последовательность является начальным отрезком

длины

, соответственно, в ней должны содержаться теперь уже

«ноль» и все прежние

единиц. Согласно лемме

эта последовательность также обладает наименьшей предсказуемостью относительно

, поэтому если вдруг окажется, что число «нулей» в ней по прежнему строго больше числа «единиц», то все наши рассуждения вместе с мысленным вычеркиванием последнего «нуля» мы можем повторить снова (рис 13b).
рис 13
Действуя таким образом, в конце концов мы вычеркнем из

в точности

стоящих на ее конце «нулей». В результате останется последовательность, состоящая из

элементов, назовем ее

, в которой количество «нулей» и «единиц» будет равным (рис 13с). По лемме

последовательность

также должна обладать минимальной предсказуемостью относительно

, однако на этот раз мы уже не можем однозначно сказать, какой
именно символ будет стоять у нее на конце!
Предположим сначала, что на конце стоит «ноль» (рис 14а). Мысленно вычеркнем этот «ноль» из последовательности. Оставшаяся часть

будет включает в себя

«ноль»,

«единиц», а еще будет обладать, согласно лемме

, минимальной предсказуемостью относительно

. Все эти факты позволяют нам утверждать, что последний символ урезанной версии

, то есть предпоследний символ самой

, уж точно должен быть единицей.
рис 14
Если бы мы предположили, что на конце

стоит не «ноль», а «единица», то из симметричных соображений необходимо бы пришли к тому выводу, что ее предпоследний элемент должен быть «нулем» (рис 14b). На самом деле, разница между этими двумя версиями

для нас не столь существенна, поскольку они обе совершенно одинаково непредсказуемы относительно

. Действительно, так как в обоих случаях двум последним элементам предшествует равное число «нулей» и «единиц», то перестановка их (двух последних элементов) местами на предсказуемость

повлиять никак не может. По сути, только что нами были доказаны следующая
Теорема 1: Последовательность, составленная из  «нулей» и
«нулей» и  , не превосходящего
, не превосходящего  , числа «единиц», будет обладать минимальной относительно
, числа «единиц», будет обладать минимальной относительно  предсказуемостью в точности тогда, когда:
предсказуемостью в точности тогда, когда:
 последние ее
последние ее  позиций будут заняты «нулями»;
позиций будут заняты «нулями»;
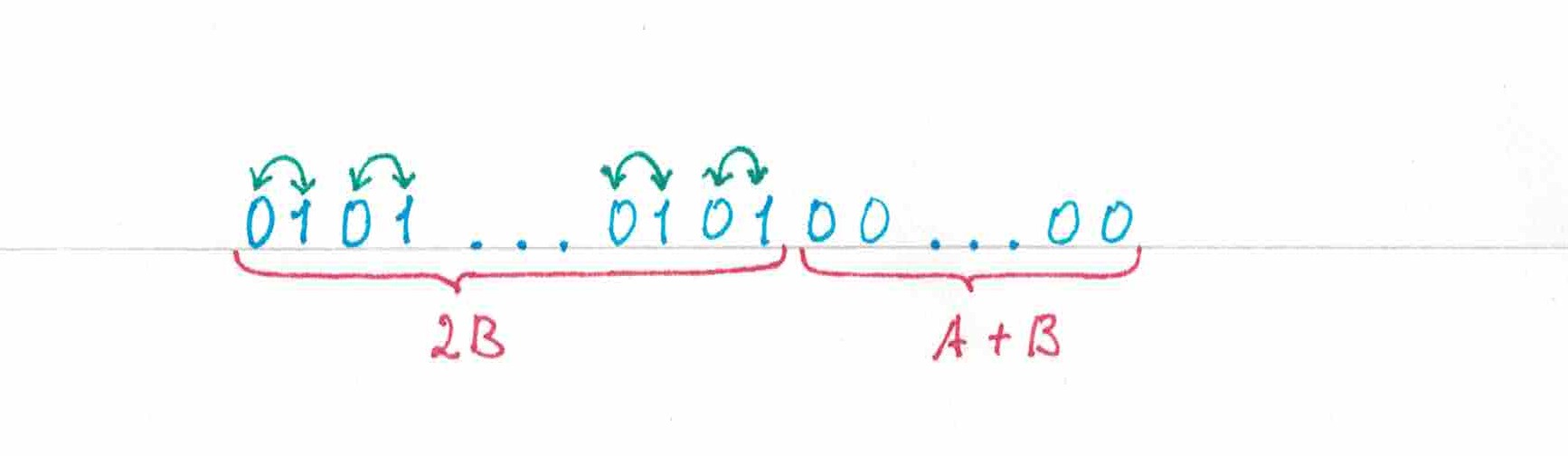
 первые ее
первые ее  элементов будут представлять из себя
элементов будут представлять из себя  последовательно расположенных пар «нуля» и «единицы», порядок символов в каждой паре может быт выбран произвольным
последовательно расположенных пар «нуля» и «единицы», порядок символов в каждой паре может быт выбран произвольным (рис 15).
рис 15
Наверное, читатель уже обратил внимание на то замечательное совпадение, что под требования теоремы

как раз-таки подходят уже хорошо знакомые нам пульсирующие последовательности префиксного типа. Параграфом раннее мы получили формулу для математического ожидания доли тех элементов в пульсирующих последовательностях, которые стратегия

по итогу сможет предсказать правильно. Теперь этот результат приобретает новый смысл и достоин быть выделен в отдельную
Теорема 2: Какова бы ни была бинарная последовательность  , математическое ожидание доли тех из ее элементов, которые стратегия
, математическое ожидание доли тех из ее элементов, которые стратегия  по итогу сможет предсказать правильно, никак не меньше чем
по итогу сможет предсказать правильно, никак не меньше чем 
, где

— это длина

,

— дисбаланс между количествами содержащихся в ней «нулей» и «единиц», а оценка

не зависит от

Промежуточные итоги
Интригующий ответ
В начале статьи был задан вопрос:
«Если количество „единиц“, которое присутствует на распечатанном участке последовательности, существенно превышает число имеющихся там „нулей“, разумно ли тогда в качестве предсказаний ее новых элементов „единицы“ называть чаще „нулей“?»
Теперь уже хорошо изученный нами пример стратегии

склоняет нас к тому, чтобы ответить на этот вопрос положительно, правда грань между истиной и заблуждением здесь куда тоньше, чем может показаться на первый взгляд. Если вы не хотите перейти этой грани, то каждый раз обязательно должны уточнять: «в каком смысле», «при каких условиях» и что значит «разумно». Давайте рассмотрим две существенно различные ситуации.
Ⅰ. Сначала предположим, что в момент, когда на ленте еще не напечатан ни один символ, вы почему-то решили прибегнуть к стратегии

. Такое решение, например, будет вполне оправданным, если вы хотите у будущей последовательности, имей она значимый дисбаланс и достаточно большую длину, угадать в среднем больше половины ее элементов, в противном же случае — не слишком сильно проиграть по количеству угаданных символов стратегии с монеткой.
Пусть прошло некоторое время, часть последовательности была напечатана, какая-то часть ваших прогнозов успела оправдаться, другая часть — нет, и в этот момент вдруг оказалось, что «единиц» на ленте больше имеющегося там количества «нулей». В данной ситуации и при данных предположениях для вас будет абсолютно
разумно подчиниться инструкциям

и в своем предсказании следующего элемента установить для «единицы» больший вероятностный вес, чем для «нуля».
Почему разумно? Потому что придерживаясь изначально выбранной стратегии, вы действительно достигните желаемого результата. Если напечатанная в итоге последовательность окажется достаточно длинной и будет иметь существенный дисбаланс, то «в среднем» вы предскажите больше половины ее элементов, а если — нет, то по количеству угаданных символов не сильно проиграете стратегии

Неужели наш мир устроен так, что будущее в нем способно как-то влиять на прошлое?
Может быть и да, но как вы увидите чуть позже, эта потенциально экстравагантная черта Вселенной к рассматриваемой здесь проблеме не имеет ровно никакого отношения. Чтобы во всем разобраться…
Ⅱ. Давайте слегка поменяем условия прошлого примера. Ваша цель остается прежней: суметь угадать в неизвестной последовательности как можно больше ее элементов. Прежней остается и стратегия, которой вы должны придерживаться, — это

. Однако на этот раз вы стартуете с момента, когда на ленте уже напечатано какое-то фиксированное и заранее известное вам число символов.
Предположим, что среди предварительно напечатанных символов «единиц» оказалось существенно больше «нулей». Должно ли это обстоятельство заставить вас в вашем первом прогнозе придать больший вероятностный вес «единице», или же все предсказания должны строиться так, как будто бы никакого заранее напечатанного участка нет?
Как ни парадоксально, но по сравнению с предыдущим примером здесь все наоборот: при вычислении вероятностных весов в очередном прогнозе вам
разумно игнорировать символы, которые до этого вы не предсказывались. Почему? Да потому, в противном случае легко подобрать такую последовательность, на которой ваш «средний» результат будет куда хуже, чем результат угадывания при помощи стратегии с монеткой (Приведите пример самостоятельно). Конечно, при каком-нибудь другом способе формализовать задачу, или при других добавочных предположениях может оказать вполне
разумным, увидев на ленте одни «единицы» в качестве своего первого предсказания назвать «единицу», однако в рамках развитого здесь подхода — это не так.
Пессимисты не приспосабливаются
Пришло время объяснить ту особую роль, которую в нашем повествовании играет стратегия угадывания символов при помощи монетки. Дело в том что среди вообще всех возможных стратегий

позволяет получить «гарантированный средний выигрыш» максимального размера. Смысл здесь таков: если взять каждую стратегию и найти, каково будет математического ожидания доли угаданных ею символов в наименее предсказуемой для нее последовательности, то именно у стратегии

эта величина окажется самой большой. Получается, что если вы — абсолютный и рациональный пессимист, то наилучшая для вас стратегия одна — это

.
Строгое доказательство, только что сделанных утверждений будет дано ниже (см лемма 3), а сейчас я бы хотел, чтобы вы акцентировали свое внимание вот на какой идее. Попытка адаптации, вообще говоря, не дается бесплатно: если алгоритм рассчитан искать и приспосабливаться к эмпирическим закономерностям, то скорее всего его наихудший результат будет меньше, чем результат, который в наихудшем для себя сценарии покажет стратегия абсолютно пессимиста (Более подробно о концепции «крайнего математического пессимизма» вы можете прочитать в предыдущей статье:
habr.com/ru/post/517070). Что касается стратегии

, то, как было показано, ее наихудший результат проигрывает наихудшему результату

на величину

.
От частного к общему
До настоящего момента содержание статьи было посвящено в основном конкретным примерам и весьма частным случаям. Такой подход позволил нам прощупать суть явления, для каких-то идей доказать их принципиальную осуществимость, для других — получить лаконичный контрпример. Однако подобные результаты редко претендуют на полноту.
Скажем, мы показали, что существуют стратегии, которые в любых достаточно длинных бинарных последовательностях со значимым дисбалансом в числе составляющих их «нулей» и «единиц», способны угадывать «в среднем» существенно больше половины их символов. Однако нами не был сформулирован вопрос о возможно «лучшей» стратегии, или стратегии, которая угадывает максимум из теоретически возможного, или способе действий, который при той же эффективности на «удобных» для него последовательностях меньше всего проигрывает стратегии пессимиста в своем наихудшем сценарии.
Разумеется, сама по себе задача предсказания дисбалансных последовательностей не является чем-то исключительно важным, на что стоит тратить свое время, если только вы не большой любитель математики. Важным является ее обобщение — вопросы об основных свойствах адаптивных алгоритмов и классах тех закономерностей, к которым эти алгоритмы созданы приспосабливаться. Например, как долго должна присутствовать в потоке данных та или иная закономерность, чтобы появилась возможность ее заметить, как долго, — чтобы приспособится и успеть извлечь из этого пользу, как связаны между собой скорость адаптации и то, насколько адаптивная стратегия проиграет в своем наихудшем сценарии поведению рационального пессимиста, как влияет наличие в данных других закономерностей на все эти процессы?
В конце концов, даже терминологическая база для описания феномена адаптации пока еще остается неясной. В оставшаяся части статьи вы найдет шуточное исследование, которое, я надеюсь, само по себе довольно увлекательно и к тому же может рассматриваться как некий эскиз общего метода решения подобных задач.
Добавление: Общая теория отгадывания дисбалансных последовательностей
Формальности
В предыдущих параграфах объектом нашего исследования были лишь несколько специально подобранных стратегий. В этом же разделе мы будем говорить вообще обо всех возможных стратегиях. Ну, или почти обо всех, а значит с самого начало важно уточнить, какой смысл вкладывается в понятие «стратегия». Под словом «стратегия» обычно понимается: «некий план действий для каждой конкретной ситуации». В нашем случае «действием» является предсказание следующего элемента последовательности, точнее, — назначение «нулю» и «единице» вероятностных весов, с которыми они в этом предсказании будут участвовать. Что касается обстоятельств, то мы не будем включать сюда мнение вашего соседа или состояние погоды над вашей головой, хотя и такие теории тоже могут быть построены. Единственное обстоятельство, котором мы действительно будем интересоваться — это то, какая последовательность символов уже присутствует на ленте в момент предсказания.
При заявленном подходе любая стратегия

есть функция, которая каждой возможной бинарной конечной последовательности

ставит в соответствие пару весов: вес «нуля»

и вес «единицы»

, где

.
Математическое ожидание
числа символов, которые стратегия

угадает в последовательности

, договоримся обозначать как

, а математическое ожидание
доли таких символов — как

.
Кто лучше?
Стремление к совершенству — одна из черт человеческой культуры, которая, понятное дело, переносится и на математику. Пусть имеются сразу две стратеги для угадывания элементов в неизвестных последовательностях: №1 и №2, как понять, какая из них лучше? Нетривиальным этот вопрос делает гипотетическая ситуация, при которой результаты первой стратегии оказываются лучше на одних последовательностях, а результаты второй — на других. Примером здесь могут служить способы угадывания, согласно первому из которых всегда называется «ноль», а согласно второму — «единица». Если на ленте в итоге будет напечатано больше «нулей», то лучший результат покажет первый способ, а если — «единиц», то — второй.
От подобной неоднозначности можно избавиться, если стратегии сравнивать по величине ожидаемого от них результата в наименее предсказуемых для них последовательностях. Обозначим как

наименьшее (точную нижнюю грань) математическое ожидание доли угаданных символов, которое стратегия

позволяет получить среди вообще
всех бинарных последовательностях, через

— ту же самую величину, но вычисленную только среди последовательностей длины

, а через

— ее же, но среди последовательностей, составленных ровно из

«нулей» и

«единиц».
Эти три оператора порождаю на множестве стратегий три различных (частичных) порядка сравнения:
«глобального»-

,
«с варьируемой длинной» —

и
«с варьируемым составом» —

.
Соответственно отношение

означает просто, что

,
далее

— что при всех значениях длин

:

,
и наконец

выполняется тогда и только тогда, когда для любых возможных

и

справедливо неравенство

.
Разумеется, если стратегия

нестрого превосходит стратегию

в порядке «с варьируемым составом», то есть

, то

нестрого превосходит

и в порядке «с варьируемой длиной»:

. Аналогично: если

нестрого превосходит стратегию

в порядке «с варьируемой длиной»:

, то обязательно

нестрого превосходит

и в «глобальном» порядке:

. А вот обратные утверждения не верны.
Так, если под

и

подразумевать соответственно стратегию всегда называть «ноль» и стратегию всегда называть «единицу», то при всех

:

(первая из них не отгадает ни одного символа в последовательности из

«единиц», а вторая — ни одного символа в последовательности из

«нулей»), поэтому в порядке

эти стратегии в некотором смысле «равны», то есть одновременно и

и

. С другой стороны в порядке

эти стратегии оказываются несравнимыми (как пианист и шеф повар ресторана), поскольку последовательности, состоящие из одних «нулей», лучше угадывает первая, а последовательности, составленные из одних «единиц» — вторая.
Чтобы получить пример, когда превосходство в «глобальном» порядке не влечет превосходства в порядке с «варьируемой длиной», в качестве

возьмем стратегию, которая угадывает символы с помощью «кривой» монетки («ноль» =

, «единица» =

), а в качестве

— нашу обычную «симметричную»

, правда с той оговоркой, что первое предсказание теперь всегда будет «нулем». При любых значениях длины, наименее предсказуемыми для

будут последовательности, состоящие из одних нулей: ожидаемый на них результат —

угаданных символов. Таким образом

. Стратегия

в очень длинных последовательностях будет угадывать почти половину их элементов, поэтому не верно, что

. В тоже время, в наихудшем для

сценарии, когда последовательность состоит из единственной «единицы», математическое ожидание угаданных ею символов будет равно нулю, это меньше, чем

, поэтому

.
Какой смысл во всех этих порядках сравнения?
Предположим, вам на выбор даны две стратегии:

и

, а сами вы заинтересованы в том, чтобы «средняя» доля угаданных символов в наихудшем возможном сценарии была максимальна.

Пусть вам известно, что на ленте могут быть напечатана только последовательность из

«нулей» и

«единиц», хотя сами величины

и

остается для вас в тайне. Пусть вам также известно, что потенциально на ленте может быть напечатана любая такая последовательность. Если при этом

, то стратегию

можно исключить из рассмотрения.

Пусть вам известно, что на ленте могут быть напечатаны только последовательности некоторой определенной, хотя и неизвестной вам длины

. Вам также известно, что потенциально может быть напечатана любая такая последовательность. Если при этом

, то стратегию

можно исключить из рассмотрения.

Пусть вам известно, что на ленте может быть напечатана вообще любая последовательность и при этом

, тогда стратегию

можно исключить из рассмотрения.
Идеальный объект
Если вы — ортодоксальный пессимист, у которого нет каких-либо предположений о длине и составе будущей последовательности, то вас должна интересовать исключительно та стратегия, которая дает наибольший

. Все необходимые сведения о подобных стратегиях содержаться в следующей
Лемма 3: Пусть  — произвольное натуральное число и на ленте может быть напечатана любая бинарная последовательность длинны
— произвольное натуральное число и на ленте может быть напечатана любая бинарная последовательность длинны  . В этих предположениях наибольшее математическое ожидание доли символов, которые стратегия угадает в наихудшем для себя сценарии, среди всех возможных стратегий обеспечивает
. В этих предположениях наибольшее математическое ожидание доли символов, которые стратегия угадает в наихудшем для себя сценарии, среди всех возможных стратегий обеспечивает  . Коротко то же самое утверждение можно записать так:
. Коротко то же самое утверждение можно записать так:
Какова бы ни была стратегия  , обязательно
, обязательно  .
Следствие: Предположим, что на ленте может быть напечатана вообще любая бинарная последовательность, тогда наибольшее математическое ожидание доли символов, которые стратегия угадает в наихудшем для себя сценарии, среди всех возможных стратегий обеспечивает
.
Следствие: Предположим, что на ленте может быть напечатана вообще любая бинарная последовательность, тогда наибольшее математическое ожидание доли символов, которые стратегия угадает в наихудшем для себя сценарии, среди всех возможных стратегий обеспечивает  . Другими словами,
. Другими словами,
Какова бы ни была стратегия  , обязательно
, обязательно  .
.
Идея доказательства леммы следующая: если я буду знать, что при некоторых обстоятельствах в следующем вашем предсказании вы придадите больший вероятностный вес, скажем, «единице», то играя против вас, я смогу воспользоваться этим и напечатать «ноль». Давайте проведем рассуждение строго.
Возьмем произвольную стратегию

. В самом начале на ленте еще ничего не напечатано, но формально — на ней уже присутствует последовательность из ноль символов, обозначим ее как

. Стратегия

должна принять

как аргумент, а в ответ выдать вероятностные веса «нуля» и «единицы». Если веса обоих символов не равны

напечатаем на ленте тот символ, для которого установлен меньший вес, в противном случае — напечатаем любой из них. Получившуюся последовательность из одного элемента обозначим как

. Какая бы из вышеуказанных альтернатив не реализовалась, математическое ожидание числа символов, которые

угадает в

не превышает

. Дальше будем рассуждатьть по индукции. Пусть, действуя описанным выше способом, мы уже напечатали

символов, составляющих вместе последовательность

. Посмотрим, имеется ли перекос между вероятностными весами «нуля» и «единицы», которые стратегия

назначит на аргументе

. Если да, то напечатаем символ, которому соответствует меньший вес, иначе — напечатаем любой из них. Получившуюся последовательность назовем

.
По индукционному предположению математическое ожидание числа символов, которые

угадает в

не превышает

. Более того оно может быть равно

только тогда, когда на всех предыдущих шагах индукции вероятностные веса «нуля» и «единицы» были раны друг другу. Следовательно все символы, из которых состоит

оказались выбранными произвольно. Чтобы результат не зависел от произвола под

в этом случае должна подразумеваться вообще любая бинарная последовательность длинны

. Понятное дело, что все вышесказанное распространяется теперь и на

, а значит индукционный шаг сделан и тем самым доказательство завершено.
По принципу симметрии
Как известно, еще издавна математики любят доказывать почти очевидные утверждения. Я думаю, многим почти очевидно, что в нашей задаче роли «нуля» и «единицы» абсолютно симметричны, и поэтому вряд ли стратегиям удастся угадать больше, либо потерять меньше, если они будут к этим двум символам относится как-то по-разному. Давайте формализуем и докажем это утверждение строго.
Сперва заметим, что кой бы ни была бинарная последовательность

у нее есть «негативный» брат-близнец — ее (знаковая)инверсия

(тильда -«альфа»). Чтобы получит

, нужно в

каждую «единицу» заменить на «ноль», а каждый «ноль» — на «единицу». При повторном действии оператор «тильда» возвращает последовательность к ее исходному виду:

.
Понятие инверсии бинарных последовательностей порождает понятие инверсии на множестве их классов. Пусть

— произвольный класс, тогда

— это класс, образованный инверсиями последовательностей из

. Как и в предыдущем случае, легко проверяется, что

.
Похожим образом можно инвертировать не только последовательности и их классы, но и стратегии. Пусть

— произвольная стратегия. Если заменим в ее определении каждое упоминания о символе «нуля» словом «единица», а каждое упоминание о символе «единица», словом «ноль», то в итоге мы как раз и получим инверсию

, обозначаемую как

. На языке алгебры инвертированная стратегия определяется так:

Как и в случае последовательностей, всегда выполняется тождество:

.
Если у нас есть преобразование, то значит должна быть и симметрия! Симметричными мы будем называть такие объекты, которые совпадают со своими инверсиями.
Бинарная последовательность совпадает со своей инверсией тогда и только тогда, когда она пуста (не содержит ни одного символа). Класс

бинарных последовательностей симметричен тогда и только тогда, когда вместе со всякой принадлежащей ему последовательностью в него входит и ее инверсия.
Симметричные стратегии — это в точности те стратегии, которые не испытывают смысловых изменений, когда в их определениях слова «ноль» и «единица» меняются местами. На любой последовательности

симметричные стратегии должны предсказывать «ноль» с той же вероятностью, что и «единицу» на последовательности

. Для примера, стратегии:

,

и

— симметричные, а вот стратегия всегда называть «ноль» — нет.
В математике имеется весьма общий способ, позволяющий из несимметричных алгебраических объектов получать симметричные. Скажем, если вы имеете дело с матрицами, то симметричными среди них считаются те, которые не меняются при транспонировании:

. Чтобы из произвольной матрицы

получить симметричную достаточно взять полусумму самой

и

:

. В том случае, когда

уже является симметричной, оператор

оставит ее вид неизменным:

.
Другой пример: действительнозначную функцию

принято называть «нечетной», если ее график симметричен относительно начала координат, то есть, при всех допустимых

справедливо тождество

. Любую действительнозначную функцию

можно симметризовать, положив

, причем, если

уже была симметричной (нечетной), то

.
По аналогии с предыдущими примерами можно ввести оператор симметризации и для стратегий. Определим его по формуле

, или в более подробной записи:

Разумеется, если стратегия

уже была симметричной, то действие оператора

на ней никак не скажется.
Конечно, не всегда симметричные стратегии столь хороши, как некоторые несимметричные. Например, ни одна симметричная стратегия не предсказывает состоящие преимущественно из «нулей» последовательности так же хорошо, как это делает

— несимметричная стратегия, суть которой состоит в том, чтобы всегда называть «ноль». Более лаконично последнюю мысль можно записать так:
Какова бы ни была

и каковы бы ни были

и

, если

симметрична и при этом

, то

. В то же время, если искать инфинум в симметричных классах, то будет справедлива
Теорема 3:Обозначим как  наименьшее (точную нижнюю грань) математическое ожидание доли тех символов, которые стратегия
наименьшее (точную нижнюю грань) математическое ожидание доли тех символов, которые стратегия  позволяет угадать в последовательностях из класса
позволяет угадать в последовательностях из класса  . Какова бы ни была стратегия
. Какова бы ни была стратегия  и класс последовательностей
и класс последовательностей  , если
, если  симметричен, то:
симметричен, то:

Чтобы доказать лемму, нам достаточно показать, что для любой последовательности

![$(4)\ \ \ \ \ \ min\left[Success(S,\alpha),\ Success(S,\widetilde{\alpha})\right] \le Success(Simm(S),\ \alpha)$](https://habrastorage.org/getpro/habr/formulas/eed/34b/de7/eed34bde786b521b12e4cabf6eae6414.svg)
Выведем сперва одно простенькое, но полезное тождество. Пусть

— произвольная последовательность, а

— не менее произвольная в ней позиция. Вероятность, с которой стратегия

угадает символ в позиции

, равно среднему арифметическому между вероятностями, с которыми его угадают

и

. В тоже время вероятность

угадать

-тый символ

в точности равна вероятности

угадать

-ый символ в последовательности

. Суммируя результат по всем позициям, мы получаем, что:

Выберем

, тогда:
![$(6)\ \ \ \ \ \ Success(Simm\left(S\right), \alpha)=\frac{1}{2}(Success(S,\alpha)\ +Success(S,\widetilde{\alpha})) \geq \\ \geq min\left[Success(S,\alpha),\ Success(S,\widetilde{\alpha})\right]$](https://habrastorage.org/getpro/habr/formulas/735/055/520/735055520470b879dd322bf174ab641c.svg)
Таким образом соотношение

установлено и доказательство теоремы можно считать завершенным.
Когда порядок не имеет значения
Все конкретные стратегии, которые мы рассмотрели до этого:

,

,

, имеют одну общую черту. Все они проявляют сходство в том, что при вычислении вероятностных весов «нуля» и «единицы» ими никак не учитывается, в каком именно порядке расположены присутствующие в этот момент на ленте символы. На языке математики сказанное означает, что ассоциированные с этими стратегиями функций

и

зависят только от

— количества «нулей» и

— количества «единиц», содержащихся в последовательности

:

и

,
Подобные стратегии я предлагаю называть
беспорядковыми или
беспорядочными — на ваш вкус.
Вполне естественно задать вопрос: насколько беспорядковые стратегии «хуже» стратегий общего вида, насколько для предсказания следующего элемента последовательности важен порядок среди ее уже напечатанных символов?
Чтобы дать этому вопросу интуитивное понимание, выберем какую-нибудь произвольную (не обязательно беспорядковую) стратегию

и две последовательности

и

длины

, отличающиеся друг от друга только порядком первых

символов. Пусть то, насколько «хороша»

, мы измеряем по среднему числу угаданных ею символов в наименее предсказуемой для нее последовательности с таким же составом, как и у

.
Насколько тогда существенно, что «среднее» число символов, которое

сумеет угадать среди элементов с

-вый по

-тый, может быть не одинаковым для

и

? Насколько для нас важно, что среди первых

элементов этих последовательностей «среднее» количество угаданных стратегией

символов тоже, вообще говоря, различно?
Можем ли мы переопределить

так, чтобы она не «ухудшилась», но при этом стала беспорядковой?
Ответом на эти вопросы будет следующая действительно сильная теорема.
Теорема 4: Какова бы ни была стратегия  , стандартным образом по ней можно построить такую беспорядковую стратегию
, стандартным образом по ней можно построить такую беспорядковую стратегию  , которая окажется не только сравнимой с
, которая окажется не только сравнимой с  в порядке «с варьируемым составом», но даже будет ее в нем нестрого превосходить:
в порядке «с варьируемым составом», но даже будет ее в нем нестрого превосходить:  .
.
Следствие: Между стратегиями

и

также будут выполнятся «неравенства»:


Нам придется отложить доказательство теоремы 4 и прежде несколько подробнее исследовать «экстремальные» свойства последовательностей, наименее предсказуемых последовательностей. Именно этому и посвящен следующий параграф.
Критические последовательности и критические стратегии
Множество всех бинарных последовательностей, состоящих из

«нулей»

«единиц», будем называть композиционным классом этих последовательностей и обозначать его как

.
Пусть

— какая-то произвольная стратегия,

— какая-то произвольная последовательность из композиционного класса

. Мы будем говорить, что последовательность

, является (одной из) наименее предсказуемых относительно относительно

в своем композиционном классе, если (и только если) для любой последовательности

из

выполняется неравенство:

Свойство последовательностей: «быть наименее предсказуемыми относительно

в своем композиционном классе», кажется похожим на свойство кривых: «иметь минимальную длину среди кривых с теми же самыми концами». Насколько эта аналогия полна?
Как известно, любой неразрывный участок наикратчайшей кривой сам является наикратчайшим путем между своими концами. Если последовательность

является наименее предсказуемой относительно

, должны ли этим свойством обладать и все ее начальные отрезки? Сформулируем вопрос строго.
Для произвольной последовательности

ее

-префикс, то есть последовательность, образованную первыми

символами

, договоримся обозначать как

. Пусть

— произвольная стратегия,

— любая последовательность, являющаяся по отношению к

одной из наименее предсказуемых в своем композиционном классе,

— произвольное натуральное число, по величине не превосходящее длину

. Будет ли последовательность

являться в своем композиционном классе одной из наименее предсказуемых относительно

?
Если стратегия

— беспорядковая, то в своем композиционном классе

обязана быть наименее предсказуемой для

последовательностью. В противном случае мы можем выполнить подходящую перестановку между первыми

символами

и сделать предсказуемость

строго хуже. Поскольку стратегия

— беспорядковя, то такая перестановка никак не повлияет на вероятности угадывания

элементов

, номера которых больше

. Отсюда следует, что предсказуемость всей

строго ухудшиться, однако это противоречит предположению, что

относительно

и так была наименее предсказуемой в своем композиционном классе.
В общем случае, когда величины весов «нуля» и «единицы» в предсказаниях

существенно зависят от порядка напечатанных на ленте символов, последнее утверждение, вообще говоря, не верно (Приведите пример). В своем композиционном классе наименее предсказуемые для

последовательности, любой префикс которых в своем композиционном классе также наименее предсказуем для

, договоримся называть
критическими (для

). Если некоторая стратегия такова, что относительно нее любая наименее предсказуемая в своем композиционном классе последовательность является критической, то
критической мы также назовем и саму эту стратегию.
Почему вообще может так случится, что имея не самый непредсказуемый префикс, целиком некоторая последовательность

в собственном композиционном классе оказывается наименее предсказуемой для

?
Символом

в дальнейшем договоримся обозначает длину последовательности

. Ситуация, когда

в своем композиционном классе является одной из наименее предсказуемых для

, но при этом последовательность

таким свойством не обладает, может возникнуть только если стратегия

на аргументе

придает уж слишком малый вес тому символу, который стоит в конце

.
Ага, кажется есть идея, как это можно было бы исправить!
Для определенности будем считать, что на конце

стоит «ноль». Число «нулей» в

обозначим буквой

, а число единиц — буквой

. Переберем все наименее предсказуемые для

последовательности, обладающие тем же составов, что и

, и найдем среди них ту (назовем ее

), на которой

придаст «нулю» наименьший вероятностный вес, а также ту (назовем ее

), на которой

придаст наименьший вероятностный вес «единице». Величину

обозначим как

, а величину

как

. Как изменится предсказуемость

, если мы переопределим значение

и положим его равным

?
Среднее количество символов, которые

угадает в

и в

связаны между собой отношением:

До переопределения величины

последовательность

имела наименьшую в своем классе предсказуемостью относительно

. Может ли тогда

быть меньше изначальной величины

?
Предположим, что может, то есть, выполняется неравенство:

В таком случае припишем к концу последовательности

дополнительный «ноль». В результате у нас получится последовательность, которую мы обозначим как

. Последовательность

принадлежит тому же композиционному классу, что и

и отличающаяся от

только, быть может, порядком своих первых

символов. Математическое ожидание количества символов, которые

угадает в

, задается формулой:

Поскольку

— одна из наименее предсказуемых для

последовательностей в композиционном классе, которому принадлежит \lnot^{|\gamma|-1}(\gamma), то:

Объединяя выражения

—

, мы получаем неравенство:

однако это неравенство напрямую противоречит изначальному предположению о том, что в своем композиционном классе

является одной из наименее предсказуемых для

последовательностью. Мы пришли к противоречию, а значит доказано, что после переопределения

на

, предсказуемость

не ухудшиться.
Если бы мы предположили, что

заканчивается «единицей», все наши рассуждения и выводы повторились бы почти дословно. Похоже, что у нас появляется интересный претендент на способ, как как улучшить стратегию

. Давайте попробуем его доработать.
Как и прежде

— это множество бинарных последовательностей, составленных из

«нулей» и

«единиц». Через

договоримся обозначать множество тех последовательностей в

, которые для стратегии

являются наименее предсказуемыми в этом классе. Формально последнее определение означает, что

и для любых

из

и

из

выполняется неравенство

Пусть

— это одна из таких последовательностей множества

, наблюдая которую

назначит «нулю» самый маленький вероятностный вес, то есть:

и для любой последовательности

из

:

Аналогично, пусть

— это одна из таких последовательностей множества

, наблюдая которую

назначит «единице» самый маленький вероятностный вес, то есть:

и для любой последовательности

из

выполняется неравенство

Сумма

и

никогда не превосходит

, но и не обязательно ей равна. Если хотя бы одно из этих чисел не ноль, положим


в противном случае примем

.
Наиболее прямой и напрашивающийся способ улучшить

состоит в следующем.
Пусть

— произвольная последовательность и в ней ровно

«нулей» и

«единиц». Определим стратегию

согласно формулам:

Теорема 5: Какова бы ни была стратегия  , стандартным образом по ней можно построить такую критическую стратегию
, стандартным образом по ней можно построить такую критическую стратегию  , которая окажется не только сравнимой с
, которая окажется не только сравнимой с  в порядке «с варьируемым составом», но даже будет ее в нем нестрого превосходить:
в порядке «с варьируемым составом», но даже будет ее в нем нестрого превосходить:  .
.
Индукцией по длине последовательностей проверим, что в качестве стратегии

мы можем взять

.
Итак нам нужно показать, что:

любой префикс всякой наименее предсказуемой для

в своем композиционном классе последовательности — сам является
наименее предсказуемой для

в своем композиционном классе
последовательностью;

для любых

и

выполняется неравенство


доказывается тривиально: стратегия

по самому своему определению — беспорядковая, выше мы показали, что все беспорядковые стратегии — критические, значит

— критическая.
Пусть

, индукцией по

докажем, что выполняется

.
Когда

утверждение

выполняется тривиальным образом.
Предположим, мы уже доказали, что для всех

и

, сумма которых меньше

, выполняется неравенство

Пусть

и

— любая пара натуральных чисел (ноль мы тоже считаем натуральным числом), сумма которых равна

, проверим, что:

Рассмотрим любую последовательность

, которая состоит в точности из

«нулей»,

«единиц» и среди таковых является наименее предсказуемой для

. Предположим, что

заканчивается «нулем» (Случай, когда на конце

стоит «единица», разбирается точно так же). При сделанном предположении префикс

состоит из

-го «нуля» и

«единиц».
Пусть, как и прежде,

— это та наименее предсказуемая для

последовательность в классе

, наблюдая которую

придает нулю наименьший вероятностный вес. Раз так, то последовательность

имеет тот же состав, что и

, и при этом:

Пусть, как и прежде,

— это та наименее наименее предсказуемая для

последовательность

, наблюдая которую

придает наименьший вероятностный вес «единице». Последовательность

имеет тот же состав, что и

, и при этом:

В то же время:


Пусть

— любая последовательность, которая состоит в точности из

«нулей»,

«единиц» и среди таковых является наименее предсказуемой уже для

. Нам придется рассмотреть две альтернативные возможности: либо на конце

стоит «ноль», либо ее последний символ — это «единица».
Предположим сначала, что

заканчивается нулем. В таком случае ее префикс

имеет такой же состав как и

. Более того, стратегия

— критическая, поэтому

является наименее предсказуемой относительно нее последовательностью. По индуктивному предположению:

Согласно определению оператора

:

Объединяя

,

,

и

, получаем требуемое неравенство:

Пусть теперь

заканчивается «единицей». На этот раз префикс

по составу будет идентичен

. Поскольку сам

снова является наименее предсказуемой относительно

последовательностью, то, еще раз воспользовавшись индуктивным предположением, имеем:

Опять же, по определению оператора

:

Объединяя

,

,

и

, снова получаем, что:

Индукционный шаг успешно сделан, а значит доказательство теоремы

, а заодно и теоремы

(

— не только критическая, но еще и беспорядковая) можно считать завершенным.
Выпуклые однородные стратегии и те последовательности, которые им труднее всего предугадать
Если вы ищите стратегию, которая при любом

в наименее предсказуемой для нее последовательности с дисбалансом

угадывает в среднем как можно большую долю символов, то согласно теоремам 3 и 4 в качестве кандидатов вам достаточно рассмотреть только симметричные и беспорядковые стратегии. Последним объясняется то особое внимание, которое мы в оставшейся части статьи будем уделять классу беспорядковых стратегий. Конкретно в этом параграфе мы займемся изучением таких беспорядковых стратегий, предсказания которых полностью определяются долями «нулей» и «единиц» в уже напечатанной части последовательности. Подобные стратегии договоримся называть
однородными.
Итак, если

— однородная страегия, то:

Последнюю запись можно сделать чуть более удобочитаемой. Для этого договоримся долю «нулей», находящихся на ленте в момент очередного предсказания, обозначать как

, а «единиц» — как

. Теперь условие того, что стратегия

однородна, можно записать так:

Все рассмотренные нами раннее конкретные стратегии:

,

и

и

— были однородными.
Чтобы задать конкретную однородную стратегию, вместо двух функции от двух переменных можно использовать всего одну функцию от одной переменной. Действительно:

поэтому достаточно задать

, далее:

откуда следует, что фактически

. На рисунке 16 показаны графики

уже хорошо на знакомых стратегий

,

,

и

.
рис 16.
Однородную стратегию

, совсем не обязательно задавать именно через

: с тем же успехом можно использовать форму представления через

,

, или

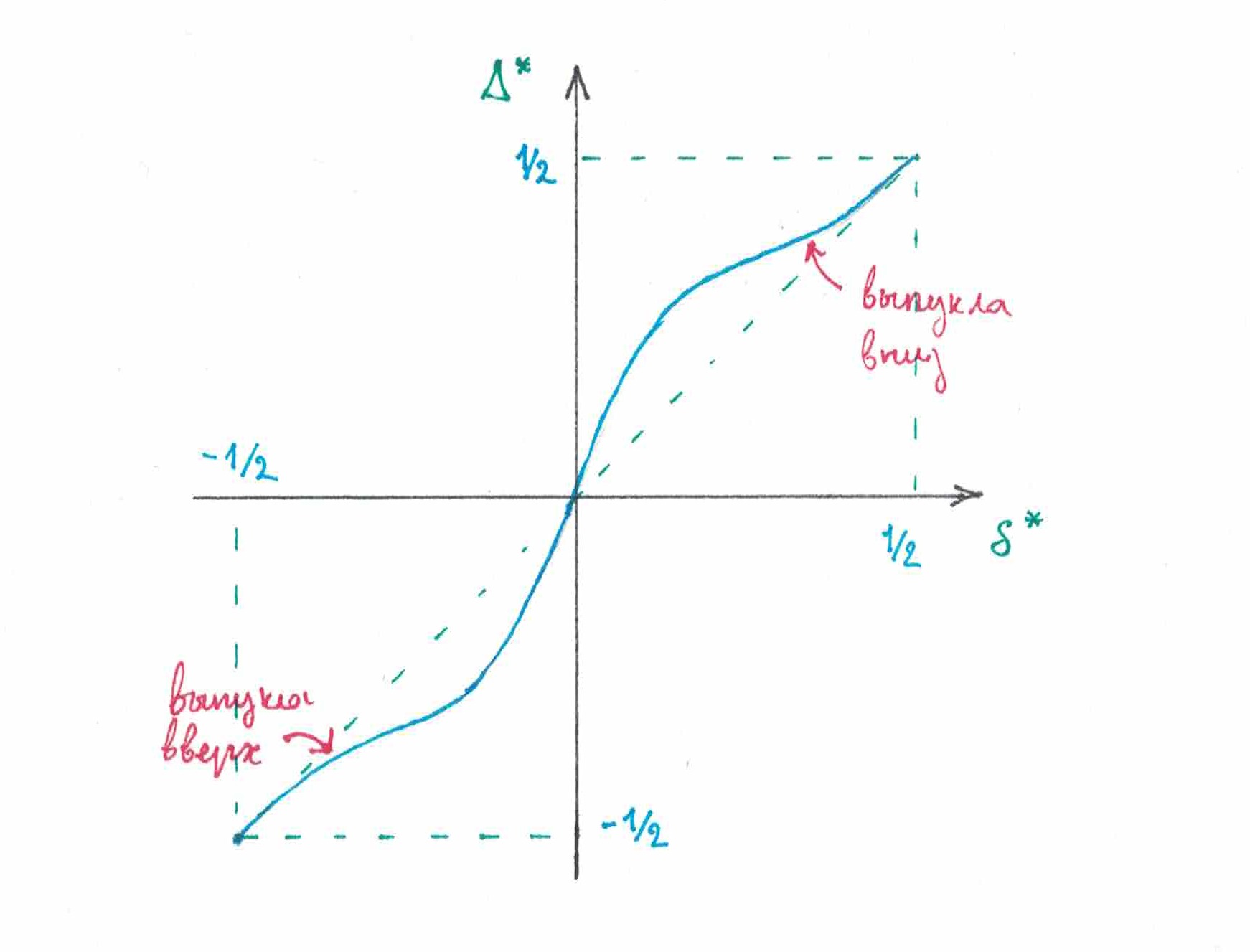
. Так как весь этот произвол не совсем удобен в нашем стратегическом анализе, попробуем изобрести способ поуниверсальнее. Введем два вспомогательных понятия. Первое из них — это текущий частотный дисбаланс «со знаком»:

второе — это дисбаланс «со знаком» между весами «нуля» и «единицы» в очередном предсказании:

При заданных

и

величина

оказывается связанной с

строгой функциональной зависимостью:

С другой стороны, если задана функция зависимости

, то тем самым полностью определены и функции

и

:

Таким образом, если стратегия однородная, то она полностью описываются своей «дельта»-функцией

. Однородная стратегия

будет симметричной тогда (и только тогда), когда ее «дельта»-функция является нечетной:

(проведите рассуждения строго). На рисунке 17 приведены графики

все тех же

,

,

и

.
рис 17
Перейдем теперь к действительно интересному вопросу. В первой части статьи было доказано, что в достаточно длинной последовательности с относительно небольшим дисбалансом

однородная стратегия

даже в худшем для себя сценарии должна отгадать примерно на

символов больше (

— длина последовательности), чем стратегия

(смотрите формулу

основного раздела и график на рисунке

).
Нельзя ли улучшить этот результат?
Давайте попробуем дать простое объяснение, почему вообще некоторым стратегиям удается угадывать больше, чем предсказанию с помощью монетки? Пусть

— это любая последовательность, в которой число «нулей» значимо превосходит число «единиц». Если так, то число «нулей» должно быть больше числа «единиц» также и во всех префиксах

начиная с некоторого значения

. Отслеживая частоту употребления «нулей» и «единиц» в префиксах, мы можем надеяться понять, который из символов будет преобладать в итоговой последовательности и тем самым суметь вовремя скорректировать свои прогнозы на более удачные.
Из такого объяснения следует, что чем чаще встречается символ в уже напечатанной части последовательности, тем больший вероятностный вес стоит ему придать в следующем предсказании. Другими словами величина дисбаланса между весами «нуля» и «единицы»

в очередном предсказании должна быть тем больше, чем больший дисбаланс

наблюдается между их частотами в уже напечатанном фрагменте угадываемой последовательности.
Интуитивно должно быть понятно, что чем активнее реагирует

на изменения

, тем большую выгоду должна извлечь стратегия из дисбаланса итоговой последовательности. Если на протяжении всего процесса печатанья наблюдаемый частотный дисбаланс

остается все время мал, то вполне очевидно, что в этом эксперименте чувствительность стратегии к изменениям

главным образом определяется значением производной

при

Вернемся к стратегии

. Производная ее «дельта»-функции в нуле (смотри рис 17) равна

. Мы знаем, что наихудшие свои результаты

показывает на пульсирующих последовательностях префиксного типа. Если дисбаланс пульсирующей последовательности мал, то мал также будет дисбаланс и любого ее префикса. Предположим, что мы хотим научится угадывать больше символов в пульсирующих последовательностях с малым дисбалансом. В таком случае сама собой возникает идея:
" А нельзя ли переопределить «дельта»-функицию стратегии

так, чтобы ее производная в нуле возросла?"
Прежде чем брать в руки карандаш и начинать чертить графики давайте перечислим некоторые самые простые ограничениях на вид

.

Мы знаем, что нет смыла рассматривать несимметричные стратегии, поэтому после переопределения

— должна остаться нечетной функцией равной

в нуле;

Разумно рассматривать только строгомонотонные зависимости

от


Область определения

является отрезком
![$[ -1/2 , \ 1/2]$](https://habrastorage.org/getpro/habr/formulas/5ca/114/834/5ca11483494ed150aab0dbb16405d596.svg)
. Поскольку ее значения — это дисбаланс вероятностных весов, то они не могут быть больше

или меньше

;

Если до настоящего момента на ленте печатались символы только одного типа (например, только «единицы»), то вполне разумно предположить, что следующий элемент последовательности будет символом того же типа. Как следствие, мы можем рассматривать лишь такие функции, для которых

и

.
При попытке удовлетворить всем перечисленным условиям я попробовал нарисовать график и то, что у меня вышло, вы видите на рисунке 18.
рис 18
Упражнение 1: Пусть однородная стратегия  такова, что производнаяs
такова, что производнаяs  в точке
в точке  равна
равна  . Пусть, также,
. Пусть, также,  — это любая пульсирующая последовательность префиксного типа, дисбаланс
— это любая пульсирующая последовательность префиксного типа, дисбаланс  которой мал по сравнению с единицей. Покажите, что с точностью до членов малости более высокого порядка
которой мал по сравнению с единицей. Покажите, что с точностью до членов малости более высокого порядка

Упрощенно можно сказать так: вместе с увеличением производной  в точке
в точке  способность однородных стратегий предугадывать пульсирующие последовательности и «штраф», который они получают за адаптацию, — растут пропорционально друг другу.
способность однородных стратегий предугадывать пульсирующие последовательности и «штраф», который они получают за адаптацию, — растут пропорционально друг другу.
Глядя на рисунок 19 трудно не заметить, что правая часть графика почти естественно получается выпуклой вверх, а левая не менее естественно — выпуклой в низ. Однородные стратегии, у которых «дельта»-функции обладают описанным свойством, договоримся называть
выпуклыми. Для однородной стратегии совсем не обязательно, чтобы ее функция

правей нуля была выпуклой вверх, а левее — выпуклой вниз. Если постараться, можно начертить и по-другому (рис 19):
рис 19
Тем не менее, выпуклые стратегии «естественны» и к тому же легко поддаются анализу, поэтому оставшуюся часть параграфа мы посвятим именно им.
Как было сказано выше (упражнение 1), однородные стратегии (в частности выпуклые однородные стратегии) тем лучше отгадывают малодисбалансные пульсирующие последовательности, чем больше у этих стратегий производная их «дельта»-функции в нуле. Однако в рамках нашего исследования куда интереснее было бы ответить на другой вопрос:
«Каким образом величина

сказывается на эффективности угадывания символов в наименее предсказуемых для данной стратегии последовательностях и, собственно, каков у этих наименее предсказуемых последовательностей вид?» Эти ответы содержаться в следующей
Теорема 6: Пусть  — произвольная выпуклая и симметричная стратегия. Бинарная последовательность
— произвольная выпуклая и симметричная стратегия. Бинарная последовательность  , состоящая из
, состоящая из  «нулей» и
«нулей» и  «единиц»
«единиц»  , тогда и только тогда будет наименее предсказуемой для
, тогда и только тогда будет наименее предсказуемой для  в своем композиционном классе, когда:
в своем композиционном классе, когда:
 последние
последние  позиций
позиций  заняты «нулями»;
заняты «нулями»;
 первые ее
первые ее  элементов представляют из себя
элементов представляют из себя  последовательно расположенных пар «нуля» и «единицы», порядок символов в каждой паре может быт выбран произвольным.
последовательно расположенных пар «нуля» и «единицы», порядок символов в каждой паре может быт выбран произвольным.
Следствие: В своем композиционном классе каждая пульсирующая последовательность префиксного типа является одной из наименее предсказуемых для всех выпуклых стратегий сразу.
Теорема

как две капли воды схожа с теоремой

, доказываются они тоже схожим способом.
Пусть

— произвольная однородная выпуклая стратегия, а

— последовательность, которая в своем композиционном классе для

является одной из наименее предсказуемых. Число «нулей» в

обозначим буквой

, а число «единиц» — буквой

. Для начала покажем, что если

, то на конце

обязан стоять «ноль».
Чтобы в последствии прийти к противоречию, предположим, что на конце

стоит «единица».
Пусть

— это позиция самого правого нуля в

, тогда последовательность

заканчивается на

и ее можно представить как

. Последовательность

включает в себя ровно

«нулей» и ровно

«единиц». Так как

и

, то

, то есть, количество «нулей» в

строго больше числа содержащихся в ней «единиц». Поскольку стратегия

— беспорядковая, то

является в своем композиционном классе одной из наименее предсказуемых для

. Последовательность

, полученную из

перестановкой ее двух последних символов, обозначим как

. Последовательности

и

имеют одинаковый состав, поэтому принадлежат одному и тому же композиционному классу. Cравним, насколько различаются математические ожидания числа тех символов, которые

сможет угадать в каждой из них.
Очевидно, что перестановка

-го

-го элементов никак не повлияет на среднее
число символов, которые

угадает среди первых

элементов этих последовательностей, и нам остается только посчитать, какие различия возникнут на двух последних элементах.
В последовательности

стоящий на предпоследнем месте «ноль» стратегия

угадает с вероятностью

а стоящую на последнем месте единицу — с вероятностью

Средняя эффективность

на

будет выражаться как

Если выполнить транспозицию, то шансы угадать ноль станут равными

а шансы угадать единицу —

Таким образом средняя эффективность

на

составит

Соответственно прирост эффективности

, вызванный перестановкой, окажется равным

Как известно, если некоторая функция

выпукла вверх, то для любых

и

из области ее определения выполняется неравенство

Доказательством может служить рисунок 20.
рис 20
Функция

по условиям — выпуклая вверх. Согласно (37)

Если подставить (38) в (36), мы получим неравенство:

Так как функция

— строго возрастающая и

то

а значит

Неравенство

говорит нам о том, что

, то есть

, не в своем композиционном классе является наименее предсказуемой относительно

, но такое возможно, только если сама

в ее композиционном классе вопреки сделанному вначале предположению не является наименее предсказуемой относительно

.
Полученное противоречие показывает, что
 Если последовательность является в своем композиционном классе наименее предсказуемой для какой-нибудь выпуклой стратегии, то она обязательно заканчиваться наиболее распространенным в ней символом. Если же в такой последовательности количество «нулей» и «единиц» одинаково, то последние два ее элемента есть либо
Если последовательность является в своем композиционном классе наименее предсказуемой для какой-нибудь выпуклой стратегии, то она обязательно заканчиваться наиболее распространенным в ней символом. Если же в такой последовательности количество «нулей» и «единиц» одинаково, то последние два ее элемента есть либо  , либо —
, либо —  .
.
Возьмем любую стратегию

, которая является не только выпуклой, но в добавок еще и симметричной и любую наименее предсказуемую в своем композиционном классе для

последовательность, составленную из равного числа «нулей» и «единиц». Как было сказано выше, на конце такой последовательности стоит либо

, либо

. Предположим, что выбранная нами последовательность заканчивается на

. Поскольку

однородна и симметрична, то поменяв местами два последних символа, мы снова получим наименее предсказуемую относительно

последовательность. Таким образом,
 если стратегия
если стратегия  выпукла и симметрична, а
выпукла и симметрична, а  — любая наименее предсказуемая в своем композиционном классе для
— любая наименее предсказуемая в своем композиционном классе для  последовательность, составленная из равного числа «нулей» и «единиц», то обе последовательности:
последовательность, составленная из равного числа «нулей» и «единиц», то обе последовательности:
 и
и

— оказываются наименее предсказуемыми относительно  в их композиционном классе.
в их композиционном классе.
Оставшаяся часть доказательства полностью повторяет доказательство теоремы

. С помощью

устанавливается, что любая последовательность из

«нулей» и

, меньшего

, «единиц», будь она в своем композиционном классе наименее предсказуемой относительно некоторой выпуклой и симметричной стратегии

, на последних

позициях содержит только «нули». Далее применяя

, доказывается, что первые

позиций в такой последовательности заняты последовательно идущими парами, каждая из которых включает ровно один «ноль» и ровно одну «единицу», неважно в каком порядке.
Best practice
Вряд ли создание какой-либо теории можно считать оправданным, если из нее нельзя извлечь простые запоминающиеся рекомендаций для решении практических задач. Представьте, что вам, ни где-то на страницах научно-популярной статьи, а в вашей собственной повседневной жизни придется однажды угадывать элементы неизвестной бинарной последовательности. Могу ли я вам для этого случая посоветовать какую-то определенную стратегию?
«Серебряную пулю» предложить вам у меня не получится, однако я разберу стратегию, которая по величине выигрыша в своем наихудшем сценарии примерно равна

, а по эффективности угадывания символов в последовательностях, имеющих существенный дисбаланс, — в некотором смысле значительно превосходит стратегии

и

.
Итак, рассмотрим однородную, выпуклую симметричную стратегию

, у которой дисбаланс весов «нуля» и «единицы» в очередном предсказании определяется как знаковый квадратный корень из половины текущего дисбаланса частот. Другими словами «дельта»-функция

вид:

где функция

— есть нечетное продолжение обычной функции

, заданная по правилу:

, если

и

, если

.
Давайте найдем, чему равен наихудший средний результат

в классе последовательностей, состоящих из

«единиц» и

«нулей».
Поскольку

— выпуклая, то одной из наименее предсказуемых для нее последовательностей в классе

будет пульсирующая последовательность префиксного типа:

.
Каждую из

«единиц», расположенных на участке пульсации, стратегия

угадает с вероятностью

. На момент, когда будет делаться прогноз для

-вого по счету нуля, на ленте уже будут присутствовать

«нулей» и

«единица», создавая тем самым наблюдаемый дисбаланс

Шансы, с которыми этот прогноз окажется верным равны

В итоге математическое ожидание количества правильно угаданных на участке пульсации символов будет выражаться формулой:

Теперь займемся «гомогенным» постфиксом

. Перед тем, как будет напечатана

из последних

«единиц», на ленте будут находится

«нулей» и

«единиц», создавая своим присутствием наблюдаемый дисбаланс

Шансы, что сделанный в этот момент прогноз окажется правильным, составят

Таким образом математическое ожидание числа угаданных на гомогенном участке символов окажется равным:

Объединяя вместе

и

, мы получаем, что математическое ожидание числа угаданных символов на всей протяженности

равно

Более-менее очевидно и это следует из

, что при фикксированном значении длинны пульсирующих последовательностей

наименее предсказуемыми
для

будут последовательности с нулевым дисбалансом, то есть такие, у которых

. В этом частном случае

превращается в:

Стоящая в конце

сумма, по сути является штрафом за адаптацию. Для больших по значению

его довольно точно можно оценить интегралом:

Вспомним теперь о стратегии

. Каждое ее предсказание — это «ноль» и «единица», взятые с вероятностями весами 1/2. Независимо от конкретного вида печатаемой на ленте последовательности, очередной ее элемент

угадает с вероятностью 50%. В среднем в последовательности длинны

правильно угаданными окажутся

элементов, причем для больших

их число будет иметь распределение близкое к нормальному со средним

и стандартным отклонением

.
Смотрите, что выходит: в своих наихудших сценариях математические ожидания эффективности

и

отличаются друг от друга на величину порядка их дисперсий, то есть по большому счету оказываются несущественными.
Теперь постараемся понять, как много стратегии

удается отгадать символов в тех последовательностях, внутри которых между «нулями» и «единицами» присутствует значимый дисбаланс. Стратегия

симметрична, поэтому

. Обе эти величины договоримся обозначать как
![${Inf}_{[N,\delta]}\left(S_{Sqrt}\right)$](https://habrastorage.org/getpro/habr/formulas/d4f/e18/4f5/d4fe184f56389f06fc434a382c3eda17.svg)
. Перепишем

в эквивалентной форме:

Поскольку

является для

одной из наименее предсказуемых последовательностей в своем композиционном классе, то
![${Inf}_{[N,\delta]}\left(S_{Sqrt}\right)=\ \frac{1}{N}Success\left(S_{Sqrt},\ \alpha\right) $](https://habrastorage.org/getpro/habr/formulas/355/fc4/478/355fc4478121c01f58b3fcb00a8b722a.svg)
, или:
![$(53)\ \ \ {Inf}_{[N,\delta]}\left(S_{Sqrt}\right)=\ \frac{1}{2}+\frac{1}{2N}\cdot\left(\sum_{i=0}^{2N |\delta| -1}\sqrt{\frac{i}{i+N(1-2|\delta| )}}\right)-\frac{1}{2N}\cdot\left(\sum_{k=0}^{N(1/2-|\delta|) -1}\frac{1}{\sqrt{2k+1}}\right)$](https://habrastorage.org/getpro/habr/formulas/379/75a/bf2/37975abf28ed6dfb8cdbf42cd7e4f121.svg)
Выражение для
![${Inf}_{[N,\delta]}\left(S_{Sqrt}\right)$](https://habrastorage.org/getpro/habr/formulas/d4f/e18/4f5/d4fe184f56389f06fc434a382c3eda17.svg)
оказывается составленной из трех слагаемых. Первое слагаемое:

— это базовая эффективность, которую можно получить безо всякой адаптации. Второе:

— положительная прибавка связанная с адаптацией. Последнее слогаемое:

— входит в

со знаком «минус», представляя собой штраф за адаптацию.
Когда

стремится к бесконечности, а

остается фиксированным, первое слагаемое никак не изменяется, третье стремится к нулю (равномерно по

). Выясним, как ведет себя второе слагаемое. Перепишем

в виде

Если

велико, то

можно с хорошей точностью заменить интегралом:

который от

никак не зависит. Таким образом при больших

:
![$(56)\ \ \ \ \ \ {Inf}_{[N,\delta]}\left(S_{Sqrt}\right)\approx\frac{1}{2}+\frac{|\delta|}{2}\cdot\int_{0}^{2}{\sqrt{\frac{t}{1/|\delta|-2+t}}dt}={\rho}_{Success}(\delta)$](https://habrastorage.org/getpro/habr/formulas/579/317/6a9/5793176a9d0f67d29ce1e948812f613e.svg)
График

представлен ниже на рисунке


рис 21.
Если сравнить графики на рисунках

и

, то можно заметить, что график функция

у стратегии

проходит заметно ближе к прямой

, чем тот же график у стратегии

. При малых по модулю

знаменатель подкоренного выражения в

равен примерно

а сама функция

:

то есть прибавка к базовым 50% угаданных символов у стратегии

асимптотически больше чем квадратичная прибавка

, которую обеспечивает стратегия

.
Это — пожалуй, все, что я хотел рассказать об угадывании дисбалансных последовательностей. В качестве развития изложенных в здесь идей позвольте предложить вам несколько интересных исследовательских проблем. Мне, правда, не известно, решались ли они кем-то раньше. Вполне может оказаться, что это новая область знания, у Вас, мой читатель, есть шанс стать пионером ее покорения.
К горизонтам новых знаний
Математическая статистика на сегодняшний день — это развитая, обширная научная дисциплина с весьма почтенной историей. Ее создание должно было решить проблему установления истин о наблюдаемом явлении в условиях, когда природа этого явления отчасти случайна и в каком-то смысле однородна во времени. Однако на деле часто бывает так, что исследуемое явление случайно, но не до конца, или так, что природа этой случайности значительно меняется в течение интересующего нас времени.
Примером первого может служить высота гор на небольшом участке горного хребта, или возраст пассажиров автобуса некоторого этнического региона. С одной стороны их эмпирическое распределение будет походить на случайное, а с другой — процессы горообразования и причины, по которым люди проживают в этой местности и едут в этот день в этом конкретном автобусе, могут рассматриваться как вполне детерминистические.
Вот другой пример: вы открыли в городском парке палатку с мороженным и исследуете спрос на свой товар. Понятное дело, что каждодневное число покупателей было бы случайным, даже если бы каждый день был солнечным июльским четвергом. Чтобы достаточно точно построить эмпирическое распределение спроса, вам потребуются данные за много дней подряд. Но дни недели разные, погода тоже разная, да и лето не вечно.
Каким образом можно было бы преодолеть описанные трудности?
Один из радикальных способов состоит в том, чтобы отказаться от предположения о случайности исследуемых явлений: пусть наблюдения будут такими, какими они будут, а мы попытаемся к ним приспособится по ходу событий. Собственно именно этот подход и был нами успешно применен для угадывания символов в неизвестных наперед последовательностях. Давайте проанализируем, в чем он состоял.
У бинарных цепочек есть такое количественное свойство — величина дисбаланса между частотами содержащихся в них «нулей» и «единиц». По условию мы не знали, в какой мере печатаемая на ленте последовательность должна им обладать, однако это не мешало нам взять монетку и с ее помощью гарантированно угадать в среднем половину всех символов. Не обязательно было угадывать с помощью монетки: нам разрешалось самим построить стратегию. Если дисбаланс в последовательности велик, то желательно было, чтобы средняя доля символов, которые в итоге угадает выбранная нами стратегия, была как можно больше

, а если дисбаланс окажется мал, то желательно, чтобы эта доля по сравнению с

-ой была не слишком мала. В итоге мы построили несколько эффективных стратегий, основывавшихся на подсчете статистик в доступном наблюдению участке последовательностей. По сути статистические методы получилось применить там, где никакой случайности не предполагалось.
Хорошо, для дискретных символьных последовательностей некий аналог невероятностной статистики построить, кажется, можно. Однако если мы решили расширить и переосмыслить всю математическую статистику, то нам еще придется разработать методы для оценки и предугадывания последовательностей с действительнозначными элементами, поскольку именно ими чаще всего и приходится заниматься на практике. Здесь появляется много трудностей и одновременно большой простор для исследований и творчества. Вот некоторые шаги, которые, как мне кажется, потребуется сделать:

Нужно предложить какой-то способ для выражения оценки неизвестного числа. Пока не ясно, чем она должна являться: тоже числом, распределением или иным математическим объектом.

Необходимо будет определится с тем, к каким именно количественным свойствам действительнозначных последовательностей мы будем приспосабливаться. Выбор конкретного свойства или набора свойств зависит от рассматриваемой практической задачи, и было бы неплохо накопить много разобранных примеров.

Если уже определены типы количественных свойств, по которым предстоит вести адаптацию, и способ выражения предиктивных оценок, то можно перебирать и анализировать предиктивные стратегии с тем, чтобы найти среди них лучшую или по крайней мере приемлемую. Здесь возникают еще две задачи. Первая — это предложить количественную меру того, насколько конкретная стратегия хорошо оценивает конкретную известную последовательность. Вторая задача задача состоит в том, чтобы предложить способ сравнения разных предиктивных стратегий в условиях, когда наперед не известно, какую именно последовательность им предстоит оценивать.
Если если Вам вдруг захочется попробовать свои силы в предложенных выше задачах, или Вы готовы предложить свой собственный подход, я буду рад поделится своими мыслями и наработками а также, насколько это в моих силах присоединится и помочь в исследованиях.
Благодарю за внимание и желаю удачи!
Сергей Коваленко.
2020 год
magnolia@bk.ru

(
Pioneer-10 на фоне Юпитера)

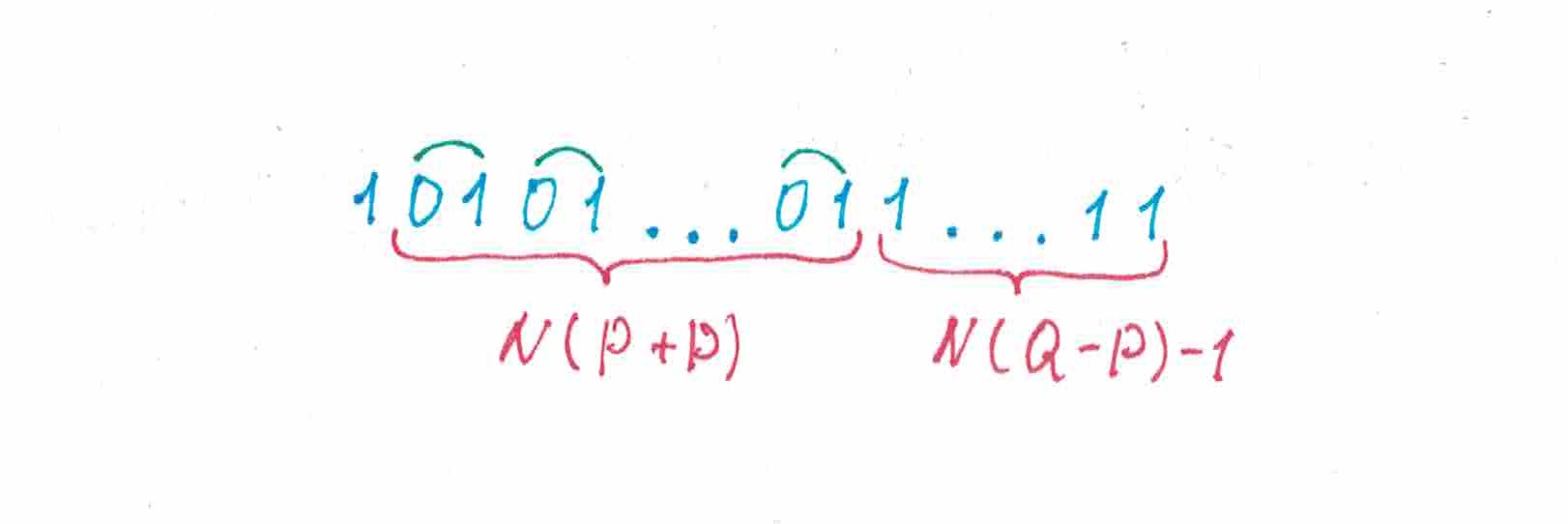
наблюдает, что единственный напечатанный символ — это «единица», следовательно прогноз второго элемента — это «единица», тем самым
ошибется в своем втором предсказании.
должна повторить свой предыдущий прогноз, то есть назвать «единицу» и ошибиться еще раз.
предскажет «ноль» и снова ошибется.

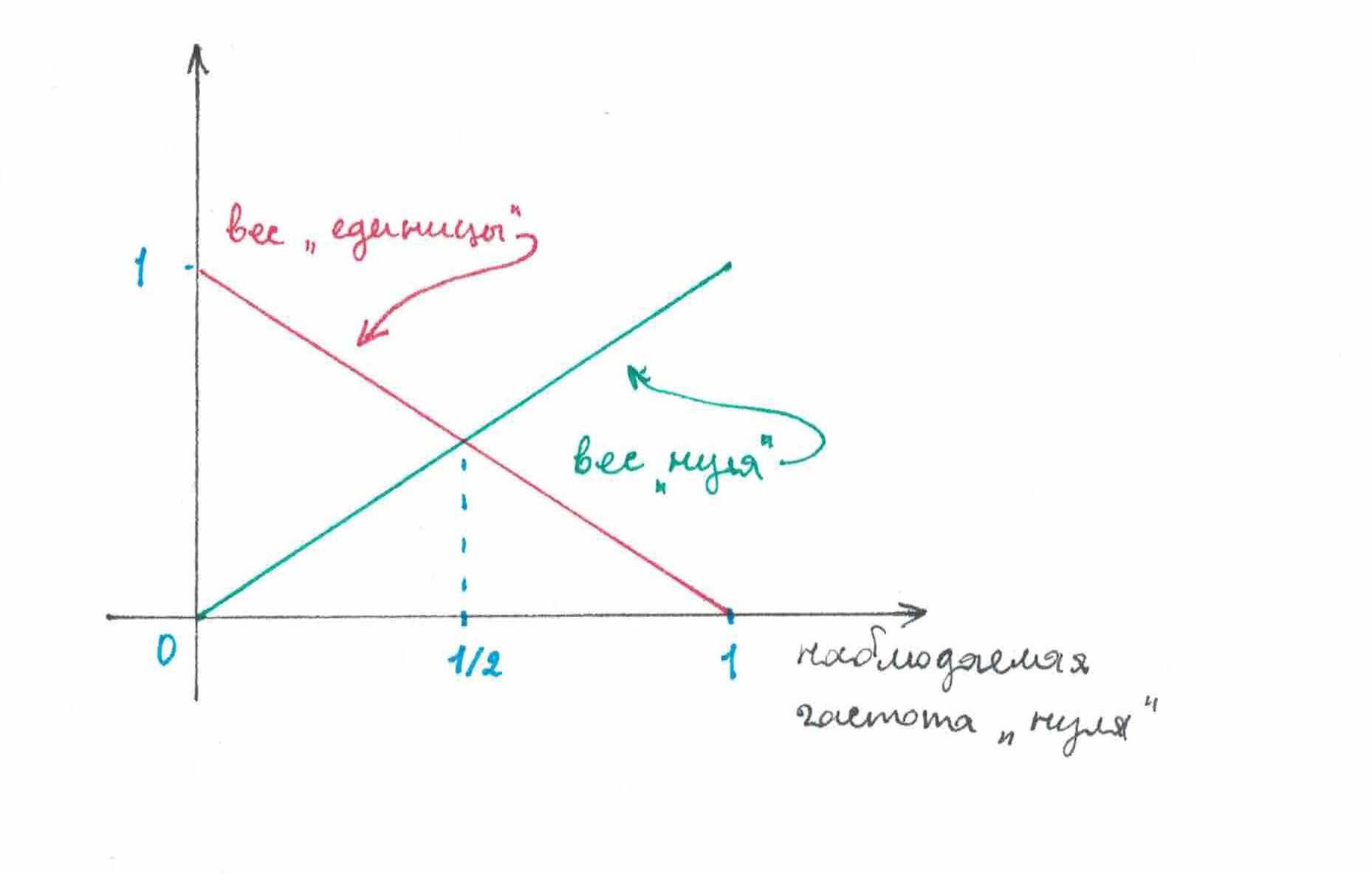

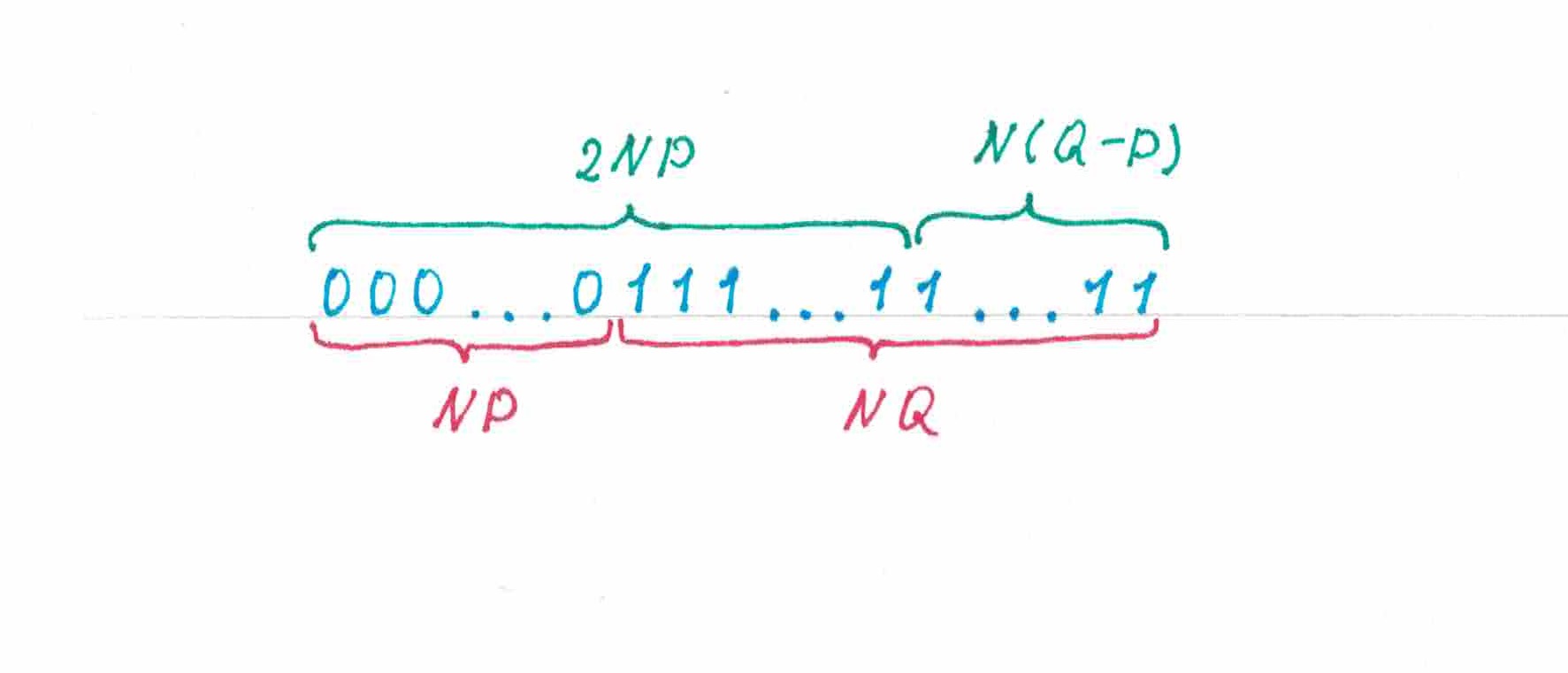
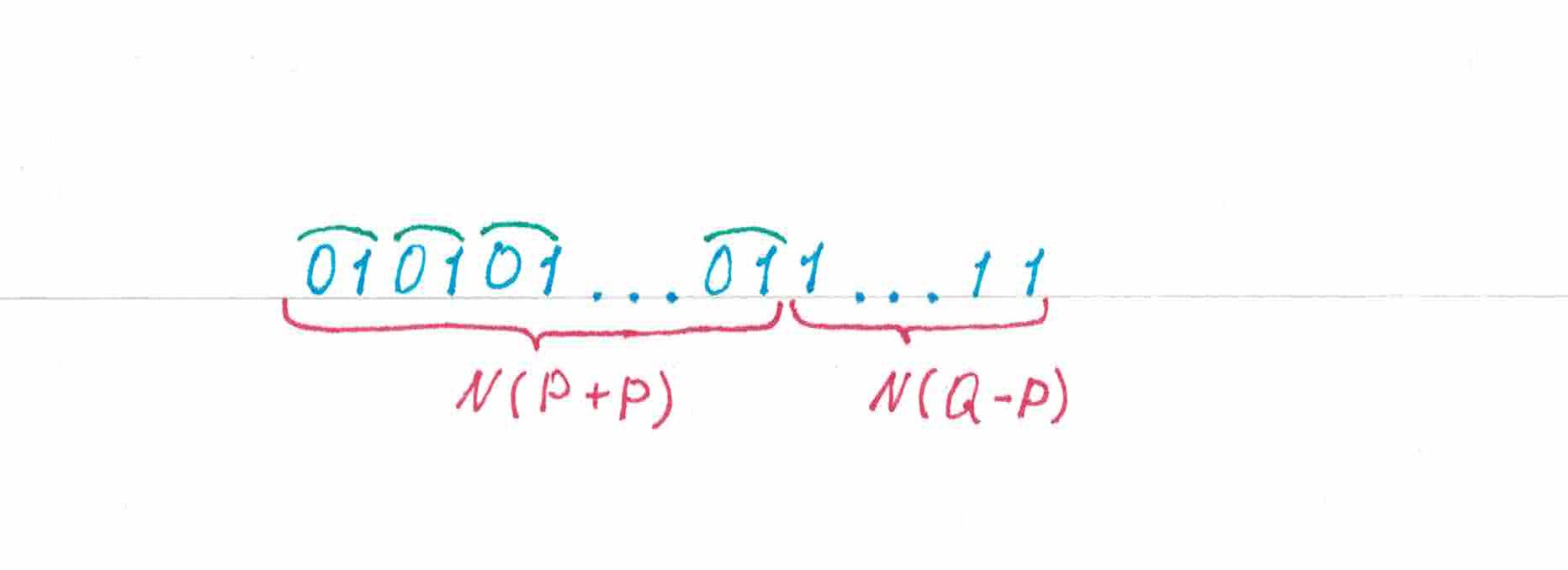
даст прогноз нуля и 100% ошибется.
«нулей» и
«единиц» (рис 8), посмотрим с какой вероятностью алгоритм угадает очередной «ноль» и очередную «единицу».

угадает его с вероятностью
. На следующем шаге «нулей» на ленте станет на один больше и вероятность угадать «единицу» будет равна
достаточно велико, мы с большой относительной точностью можем заменить сумму интегралом:
на отрезке «пульсации», составит:
на
, то же самое можно выразить и в другой форме:
следующих за ним «единиц» «гомогенного» участка (рис 9).

«нулей» и
«единица», а значит вероятность того, что предсказание, сделанное
, окажется единицей, есть
«единиц» «гомогенного» участка в среднем правильно предсказанными окажутся:
мало по сравнению с
, что по сути эквивалентно условию
или тому, что
и
являются величинами одного порядка или даже
много больше
. То же самое может быть выражено требованием, чтобы дисбаланс
был соизмерим с единицей.
, то мы можем переписать:
выражение является суммой арифметической прогрессии, вычислить которую не составит большого труда:
и используя тот факт, что
, мы получим:
и малых значениях
среди
«единиц» «гомогенного» участка правильно предсказанными в среднем окажутся примерно:
. Поскольку теперь предполагается, что диапазон изменения
велик, то входящую в
сумму с хорошей точностью можно заменить интегралом:
, мы получаем, что когда
соизмерима с единицей, число угаданных символов «гомогенного» отрезка асимптотически может быть представлено как: