Это короткая статья о том, как я воспользовался APL для проверки своих комбинаторных вычислений.
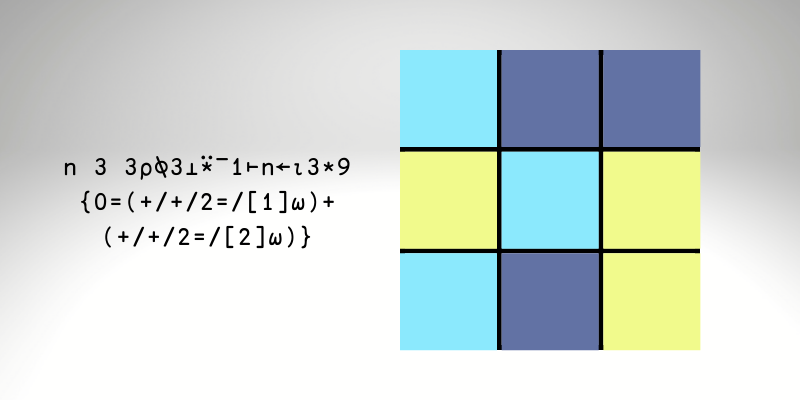
Наш местный университет проводит еженедельные соревнования по математическим задачам, которые может решать любой. На прошлой неделе задача относилась к комбинаторике и звучала следующим образом:
«Есть сетка 3 на 3 из квадратов, образующая мозаику. Сколькими способами мы можем раскрасить эту мозаику, если у нас есть 3 цвета и соседние квадраты не могут быть одного цвета?»
Под «соседними» понимаются соседние по вертикали или горизонтали. Авторы задачи дали подсказку (если не хотите спойлеров, то сразу переходите к следующему разделу!):
Комбинаторика никогда не была моей сильной стороной, но я хотел решить эту задачу. Я сел и начал прикидывать решение.
Завершив вычисления, я решил быстренько проверить своё решение при помощи APL — очень милого языка программирования, который я изучал в течение последних двух лет.
Это статья о том, как я за 30 секунд проверил на APL своё решение задачи.
Ниже представлено моё исходное решение изложенной выше задачи. В качестве упражнения попробуйте найти изъяны в моих рассуждениях и вычислениях. Поехали.
«Как и сказано в подсказке к формулировке задачи, пронумеруем квадраты в сетке:
Теперь мы изучим все возможные комбинации цветов как функцию цветов, связанную с квадратами 2, 4, 6 и 8.
Чётные квадраты могут использовать только до 2 цветов, в противном случае для квадрата 5 не останется допустимого цвета.
Предположим, что чётные квадраты имеют один цвет. В таком случае нечётные квадраты можно раскрашивать произвольным образом. Это даёт нам в сумме мозаик.
мозаик.
Теперь давайте предположим, что чётные квадраты имеют 2 цвета. Давайте зафиксируем цвет квадрата 2, который может быть любым из трёх доступных цветов. Далее есть один, два или три квадрата с цветом, отличающимся от квадрата 2, но одинаковым между ними. Рассмотрим каждый из этих трёх случаев по отдельности.
Начнём с предположения о том, что есть только один квадрат, отличающийся цветом от цвета квадрата 2. Этот цвет может быть только одним из двух. Далее нам нужно выяснить, сколькими способами мы можем раскрасить нечётные квадраты. Это будет зависеть от позиции чётного квадрата, цвет которого отличается от цвета квадрата 2. Существует три возможных схемы, где
Все эти случаи дают одинаковое общее количество различных раскрасок, потому что они являются поворотами друг друга, поэтому давайте рассмотрим только случай 1. В случае 1 квадраты 1 и 7 могут иметь 2 разных цвета каждый. Цвета квадратов 3, 5 и 9 фиксированы. Следовательно, если квадрат 2 имеет фиксированный цвет, а только один из других чётных квадратов имеет цвет, отличающийся от квадрата 2, мы получаем в сумме вариантов раскраски.
вариантов раскраски.
Теперь предположим, что квадрат 2 имеет фиксированный цвет, и есть два других чётных квадрата с цветом, отличающимся от цвета квадрата 2:
Случай 1 имеет 6 вариантов раскраски. Случаи 2 и 3 имеют по раскрасок каждый, суммарно
раскрасок каждый, суммарно  раскрасок.
раскрасок.
Единственный сценарий, который мы не учли — когда квадрат 2 имеет фиксированный цвет, а все остальные чётные квадраты имеют другой цвет:
Этот случай имеет раскрасок.
раскрасок.
Следовательно, в общей сумме мы получили
То есть, согласно моим вычислениям, существует 879 уникальных вариантов раскраски».
Увы, мои вычисления ошибочны. Но на данном этапе я ещё об этом не знал. (А вам уже удалось найти ошибки?)
На этом этапе мне захотелось убедиться, что я делаю всё правильно. Для этого я просто открыл интерпретатор APL и быстренько написал код для проверки своего решения.
Мой код делал следующее: генерировал все возможные мозаики, исключал те, которые не удовлетворяют требованию наличия разных цветов у соседних квадратов, и подсчитывал допустимые комбинации.
Сгенерировать все возможные мозаики проще некуда.
(Спойлер: это касается и остальных шагов!)
Я решил, что закодирую 3 разных цвета как 0, 1 и 2, то есть мне достаточно сгенерировать все матрицы 3 на 3, содержащие все комбинации 0, 1 и 2 во всех позициях.
Я подумал, что можно сгенерировать все последовательности (размера 9) всех трёх чисел, а затем преобразовать эти последовательности в соответствующие матрицы, обозначающие сетку.
Следовательно, я преобразовывал
в
Мне достаточно было просто сгенерировать все возможные последовательности.
Когда вам нужно сгенерировать последовательности фиксированного размера, содержащие все комбинации набора чисел, то помните, что для этого, возможно, подойдёт decode (
Если вкратце, то все нужные нам последовательности можно рассматривать как цифры числа по основанию, соответствующему количеству различных цветов.
Например, показанную выше последовательность можно рассматривать как число 2537 в троичной системе:
Мы знаем, что нам нужно последовательностей, поэтому мы просто генерируем все цифры от
последовательностей, поэтому мы просто генерируем все цифры от  до
до  и преобразуем их в троичный вид:
и преобразуем их в троичный вид:
Теперь нужно преобразовать каждый столбец в соответствующую мозаику. Это просто, нужно сначала транспонировать массив, а затем использовать оператор ранга (
Теперь, когда у нас есть все сеток, нам нужно подсчитать только те из них, которые допустимы.
сеток, нам нужно подсчитать только те из них, которые допустимы.
Воспользовавшись n-мерном редуцированием при помощи функции равенства (
Теперь нам просто нужно применить эту проверку для всех сеток. Мы снова можем воспользоваться оператором ранга (
Если мы создадим функцию, проверяющую допустимость сетки, а затем применим её ко всем сеткам, то сможем суммировать результат и получить количество допустимых сеток:
Как видите, получен ответ 246, а не 879.
В этой статье я рассказываю всю историю подробно, но когда я делал это сам, то для получения ответа на APL мне понадобилось 30-60 секунд.
Любопытно то, что я всё равно доверяю своим комбинаторным навыкам больше, чем своим навыкам APL (а это глупо!), а поэтому несколько минут смотрел на свой короткий код на APL, задаваясь вопросом, не сделал ли я ошибку в программе.
Спустя какое-то время я подумал «А что если ошибочны мои вычисления?».
Снова взглянув на свои вычисления, я заметил совершённую оплошность:
«Предположим, что чётные квадраты имеют один цвет. В таком случае нечётные квадраты можно раскрашивать произвольным образом. Это даёт нам в сумме мозаик».
мозаик».
Это неверно! Если все чётные квадраты имеют один цвет, то пяти нечётным квадратам можно выбрать один из двух оставшихся цветов, что даёт суммарно мозаик, а не
мозаик, а не  .
.
Подставив это новое число в готовые вычисления, мы получим
И теперь мои вычисления верны!
На этом этапе я был доволен проделанной работой и уже готовился отправить решение авторам задачи. Но прежде чем сделать это, я ради хвастовства вставил в конец своего решения все 246 допустимых сеток.
Как оказалось, их легко получить при помощи APL:
После всего этого я решил вернуться к своему коду на APL и посмотреть, можно ли его улучшить.
В конце концов, я довольно часто использовал
Как оказалось, это возможно (и неудивительно)!
Во-первых, для генерации всех сеток нужно подходящее преобразование
Во-вторых, я могу выполнить проверки соседства для целого 3D-массива! Достаточно просто использовать для этого нужную ось:
Чтобы скомбинировать эти две редукции, приводящие к получению двух 3D-массивов разной формы, я просто редуцировал каждый по отдельности при помощи вектора:
В конце мы суммируем их и ищем сетки без соседних квадратов с одинаковыми цветами:
Великолепно. Для написания «всего этого кода» (на самом деле, двух коротких строк!) не понадобилось никаких усилий. Потребовалось гораздо больше времени на написание статьи, чем на код!
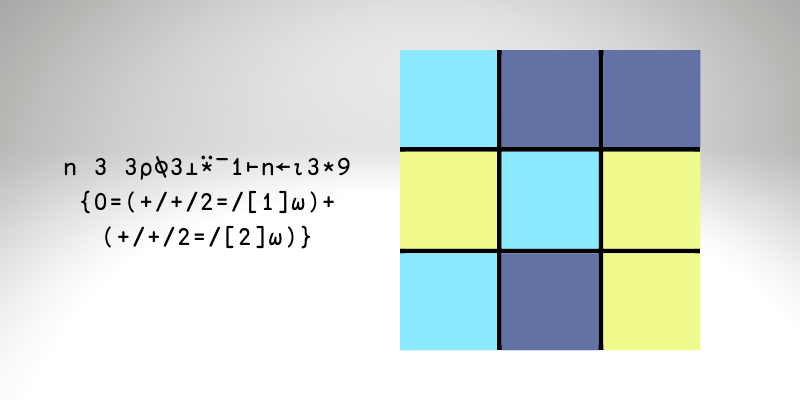
Преамбула
Наш местный университет проводит еженедельные соревнования по математическим задачам, которые может решать любой. На прошлой неделе задача относилась к комбинаторике и звучала следующим образом:
«Есть сетка 3 на 3 из квадратов, образующая мозаику. Сколькими способами мы можем раскрасить эту мозаику, если у нас есть 3 цвета и соседние квадраты не могут быть одного цвета?»
Под «соседними» понимаются соседние по вертикали или горизонтали. Авторы задачи дали подсказку (если не хотите спойлеров, то сразу переходите к следующему разделу!):
Подсказка
«Пронумеруйте квадраты от 1 до 9, а затем поработайте с цветами чётных квадратов. Это позволит определить цвета нечётных квадратов».
Комбинаторика никогда не была моей сильной стороной, но я хотел решить эту задачу. Я сел и начал прикидывать решение.
Завершив вычисления, я решил быстренько проверить своё решение при помощи APL — очень милого языка программирования, который я изучал в течение последних двух лет.
Это статья о том, как я за 30 секунд проверил на APL своё решение задачи.
- Я начну с демонстрации моего ошибочного доказательства (в том виде, в котором я его записал);
- Затем я расскажу, что сделал на APL, чтобы проверить своё решение;
- Далее я покажу свою исходную ошибку, и наконец
- Я ещё немного поработаю с кодом на APL, чтобы сделать его чище.
Моё исходное решение
Ниже представлено моё исходное решение изложенной выше задачи. В качестве упражнения попробуйте найти изъяны в моих рассуждениях и вычислениях. Поехали.
«Как и сказано в подсказке к формулировке задачи, пронумеруем квадраты в сетке:
1 2 3
4 5 6
7 8 9Теперь мы изучим все возможные комбинации цветов как функцию цветов, связанную с квадратами 2, 4, 6 и 8.
Чётные квадраты могут использовать только до 2 цветов, в противном случае для квадрата 5 не останется допустимого цвета.
Предположим, что чётные квадраты имеют один цвет. В таком случае нечётные квадраты можно раскрашивать произвольным образом. Это даёт нам в сумме
Теперь давайте предположим, что чётные квадраты имеют 2 цвета. Давайте зафиксируем цвет квадрата 2, который может быть любым из трёх доступных цветов. Далее есть один, два или три квадрата с цветом, отличающимся от квадрата 2, но одинаковым между ними. Рассмотрим каждый из этих трёх случаев по отдельности.
Начнём с предположения о том, что есть только один квадрат, отличающийся цветом от цвета квадрата 2. Этот цвет может быть только одним из двух. Далее нам нужно выяснить, сколькими способами мы можем раскрасить нечётные квадраты. Это будет зависеть от позиции чётного квадрата, цвет которого отличается от цвета квадрата 2. Существует три возможных схемы, где
⎕ обозначает цвет квадрата 2, X обозначает цвет другого квадрата, а ? обозначает неизвестный цвет нечётных квадратов:- Случай 1
? ⎕ ?
⎕ ? X
? ⎕ ?- Случай 2
? ⎕ ?
X ? ⎕
? ⎕ ?- Случай 3
? ⎕ ?
⎕ ? ⎕
? X ?Все эти случаи дают одинаковое общее количество различных раскрасок, потому что они являются поворотами друг друга, поэтому давайте рассмотрим только случай 1. В случае 1 квадраты 1 и 7 могут иметь 2 разных цвета каждый. Цвета квадратов 3, 5 и 9 фиксированы. Следовательно, если квадрат 2 имеет фиксированный цвет, а только один из других чётных квадратов имеет цвет, отличающийся от квадрата 2, мы получаем в сумме
Теперь предположим, что квадрат 2 имеет фиксированный цвет, и есть два других чётных квадрата с цветом, отличающимся от цвета квадрата 2:
- Случай 1
? ⎕ ?
X ? X
? ⎕ ?- Случай 2
? ⎕ ?
⎕ ? X
? X ?- Случай 3
? ⎕ ?
X ? ⎕
? X ?Случай 1 имеет 6 вариантов раскраски. Случаи 2 и 3 имеют по
Единственный сценарий, который мы не учли — когда квадрат 2 имеет фиксированный цвет, а все остальные чётные квадраты имеют другой цвет:
- Случай 1
? ⎕ ?
X ? X
? X ?Этот случай имеет
Следовательно, в общей сумме мы получили
То есть, согласно моим вычислениям, существует 879 уникальных вариантов раскраски».
Увы, мои вычисления ошибочны. Но на данном этапе я ещё об этом не знал. (А вам уже удалось найти ошибки?)
Проверка решения с помощью APL
На этом этапе мне захотелось убедиться, что я делаю всё правильно. Для этого я просто открыл интерпретатор APL и быстренько написал код для проверки своего решения.
Мой код делал следующее: генерировал все возможные мозаики, исключал те, которые не удовлетворяют требованию наличия разных цветов у соседних квадратов, и подсчитывал допустимые комбинации.
Генерируем все возможные мозаики
Сгенерировать все возможные мозаики проще некуда.
(Спойлер: это касается и остальных шагов!)
Я решил, что закодирую 3 разных цвета как 0, 1 и 2, то есть мне достаточно сгенерировать все матрицы 3 на 3, содержащие все комбинации 0, 1 и 2 во всех позициях.
Я подумал, что можно сгенерировать все последовательности (размера 9) всех трёх чисел, а затем преобразовать эти последовательности в соответствующие матрицы, обозначающие сетку.
Следовательно, я преобразовывал
seq
0 1 0 1 1 0 2 2 2в
3 3⍴seq
0 1 0
1 1 0
2 2 2Мне достаточно было просто сгенерировать все возможные последовательности.
Когда вам нужно сгенерировать последовательности фиксированного размера, содержащие все комбинации набора чисел, то помните, что для этого, возможно, подойдёт decode (
⊥).Если вкратце, то все нужные нам последовательности можно рассматривать как цифры числа по основанию, соответствующему количеству различных цветов.
Например, показанную выше последовательность можно рассматривать как число 2537 в троичной системе:
3⊥seq
2537
3⊥⍣¯1⊢2537
1 0 1 1 0 2 2 2
seq ⍝ the leading 0 is missing from this example.
0 1 0 1 1 0 2 2 2Мы знаем, что нам нужно
3⊥⍣¯1⊢⍳3*9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 ...
0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 2 2 2 0 0 0 1 1 ...
0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 ...Теперь нужно преобразовать каждый столбец в соответствующую мозаику. Это просто, нужно сначала транспонировать массив, а затем использовать оператор ранга (
⍤) для преобразования каждой строки матрицы: boards ← 3 3∘⍴⍤1⍉3⊥⍣¯1⊢⍳3*9
4↑boards
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 1
0 0 0
0 0 0
0 0 2
0 0 0
0 0 0
0 1 0Теперь, когда у нас есть все
Проверяем допустимость сеток
Воспользовавшись n-мерном редуцированием при помощи функции равенства (
=) мы можем легко проверить, имеют ли соседние квадраты один цвет: board ← 3 3⍴seq
board
0 1 0
1 1 0
2 2 2
2=/board
0 0
1 0
1 1
2=⌿board
0 1 1
0 0 0Подсчитываем допустимые сетки
Теперь нам просто нужно применить эту проверку для всех сеток. Мы снова можем воспользоваться оператором ранга (
⍤), чтобы применить функцию к каждой подматрице в трёхмерном массиве boards.Если мы создадим функцию, проверяющую допустимость сетки, а затем применим её ко всем сеткам, то сможем суммировать результат и получить количество допустимых сеток:
Valid ← {0=+/(2=⌿⍵),⍥,2=/⍵}
Valid board
0
+⌿Valid⍤2⊢boards
246Как видите, получен ответ 246, а не 879.
В этой статье я рассказываю всю историю подробно, но когда я делал это сам, то для получения ответа на APL мне понадобилось 30-60 секунд.
Любопытно то, что я всё равно доверяю своим комбинаторным навыкам больше, чем своим навыкам APL (а это глупо!), а поэтому несколько минут смотрел на свой короткий код на APL, задаваясь вопросом, не сделал ли я ошибку в программе.
Спустя какое-то время я подумал «А что если ошибочны мои вычисления?».
Ошибка в математическом решении
Снова взглянув на свои вычисления, я заметил совершённую оплошность:
«Предположим, что чётные квадраты имеют один цвет. В таком случае нечётные квадраты можно раскрашивать произвольным образом. Это даёт нам в сумме
Это неверно! Если все чётные квадраты имеют один цвет, то пяти нечётным квадратам можно выбрать один из двух оставшихся цветов, что даёт суммарно
Подставив это новое число в готовые вычисления, мы получим
И теперь мои вычисления верны!
На этом этапе я был доволен проделанной работой и уже готовился отправить решение авторам задачи. Но прежде чем сделать это, я ради хвастовства вставил в конец своего решения все 246 допустимых сеток.
Как оказалось, их легко получить при помощи APL:
boards⌿⍨Valid⍤2⊢boards
0 1 0
1 0 1
0 1 0
0 1 0
1 0 1
0 1 2
0 1 0
1 0 1
0 2 0
0 1 0
1 0 1
2 1 0
...Совершенствуем код на APL
После всего этого я решил вернуться к своему коду на APL и посмотреть, можно ли его улучшить.
В конце концов, я довольно часто использовал
⍤ в стиле циклов. Я хотел понять, можно ли сделать код более ориентированным на массивы.Как оказалось, это возможно (и неудивительно)!
Во-первых, для генерации всех сеток нужно подходящее преобразование
⍴: boards ← n 3 3⍴⍉3⊥⍣¯1⊢⍳n ← 3*9
4↑boards
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 1
0 0 0
0 0 0
0 0 2
0 0 0
0 0 0
0 1 0Во-вторых, я могу выполнить проверки соседства для целого 3D-массива! Достаточно просто использовать для этого нужную ось:
2=⌿[1]boards
1 1 1
1 1 1
1 1 1
1 1 0
1 1 1
1 1 0
1 1 1
1 0 1
...
2=⌿[2]boards
1 1
1 1
1 1
1 1
1 1
1 0
1 1
1 1
1 0
1 1
1 1
0 0
...Чтобы скомбинировать эти две редукции, приводящие к получению двух 3D-массивов разной формы, я просто редуцировал каждый по отдельности при помощи вектора:
- один проверяет, какая из сеток имеет соседние одинаковые цвета по вертикали
- другой проверяет, какая из сеток имеет соседние одинаковые цвета по горизонтали.
В конце мы суммируем их и ищем сетки без соседних квадратов с одинаковыми цветами:
valid ← 0=(+/+/2=/[1]boards)+(+/+/2=/[2]boards)
+/valid
246
4↑valid⌿boards
0 1 0
1 0 1
0 1 0
0 1 0
1 0 1
0 1 2
0 1 0
1 0 1
0 2 0
0 1 0
1 0 1
2 1 0Великолепно. Для написания «всего этого кода» (на самом деле, двух коротких строк!) не понадобилось никаких усилий. Потребовалось гораздо больше времени на написание статьи, чем на код!