Comments 33
И почему производная экспоненты равна 0?
Вы ведь сами показали, что в случае, например, f(x) = 2^x производная равна log2(e) * 2^x, что не равно нулю собственно говоря нигде.
Простите за токсичность, но название вашего канала играет новыми красками :)
так нам надо не чтоб дробь была равна 1, а предел дроби был равен 1.
нет я не оспариваю исходного утверждения, это я придираюсь (в математике так принято)
восклицательный знак в конце я бы не ставил. а то мне за ним начинает мерещиться гамма-функция, зачем нам всё это. ну ладно, моя личная заморочка.
ну а эллипс в школе учили рисовать двумя канцелярскими кнопкам и ниткой. используя определение эллипса как ГМТ, для которых сумма расстояний (и т.д. и т.п)
ну да, подписался на канал есть такое
Как-то несолидно вести математический канал, и не владеть LaTeXом.
Вкусовщина. Мне это напомнило презентации и проходные статьи прошлого века, когда большая часть текста печаталась, а формулы вписывались вручную. Впрочем, я те времена вживую не застал, но материалы-то живы ещё.
P.S. в discord есть боты, которые парсят tex-вставки в сообщениях пользователей и сразу рендерят их в виде картинок. А как автор ведёт свой канал без подобного?
Я нежно люблю LaTeX, всегда им пользуюсь, и при прочтении статьи была такая же мысль. Но, тем не менее, мне эти записи на бумажке показались уютными и ламповыми, вызвали положительные эмоции. Кто из нас не писал формулы на обороте конверта, когда припекло? Тем и прекрасна математика, что суть можно хоть на банановой кожуре выразить.
зато на мобилке все видно
одно из решений
Любопытно, но это единственное решение этого уравнения (с точностью до константы). Нет других функций, которые были бы производными самих себя.
Почему производная экспоненты равна ей самой?
ПО ОПРЕДЕЛЕНИЮ экспоненты, потому что неперово число является результатом решения уравнения в котором степенная функция равна производной от себя.
Точно так же можно задавать вопрос "почему функция икс_в_квадрате равна функции икс_умножить_на_икс". Ответом тоже будет "по определению".
степенная функция
показательная функция?
Только определение не уникально; правильнее было бы сказать "по одному из определений". Лично мне экспоненциальную функцию вводили как предел lim (1+x/n)^n.
Впрочем, у нас преподаватель анализа был оригинален, и даже производную определял как коэффициент второго члена ряда Тейлора функции в точке.
А как он объяснял сам ряд Тейлора до введения понятия производной?
вот да об чем и речь. по одному из определений.
вот если бы автор доказал, что они эквивалентны, то было бы неплохо.
т.е. сначала для последовательности: она возрастает, ограничена сверху, значит есть предел. обзовем его "е".
и пусть докажет, что показательная функция e^x с таким вот "е" (введенным как предел последовательности) обладает заявленным свойством.
Почему производная экспоненты равна ей самой?
Это вы её еще интегрировать не пробовали!
Сдается мне, что ответ на вопрос поста прост как 5 копеек - данная функция может быть определена как частное решение дифференциального уравнения
y'(x) = y(x)
откуда и следует ответ, очевидный из уравнения
Не обижайтесь только, но вы только что доказали, что отношение длины окружности к диаметру равно pi, воспользовавшись школьной формулой для длины окружности. Но это не доказательство, а тавтология.
Анекдот на тему.
Попал студент в психушку. Новенький, его бывалые пациенты обступили, смотрят, трогают, в общем достали. Ему надоело, и он рыкнул:
- Сейчас я вас всех продифференцирую!
Половина смылась. Он ещё раз:
- Сейчас я вас всех проинтегрирую!
Смылась другая половина. Остался один псих. Студент ему:
- А ты, что, меня не боишься!?
- А я - e в степени икс!
Интересная статья, спасибо!
Как вообще модераторы такое пропускают? В последнее время всё больше околонаучных статей на хабре либо не имеют отношения к науке, либо пишутся фриками.
Камрад, плюньте вы на математику и займитесь русским языком, с ним у вас серьезные проблемы. Когда я читаю ваше "многие из Вас ...' – у меня кровь из глаз течёт. Запомните, "вы" и "вас" никогда не пишутся с большой буквы при обращении к нескольким людям сразу. Скажу больше: писать "Вы" и при обращении к одному лицу не нужно почти никогда. Нужно всего в трёх случаях, поинтересуйтесь сами, в каких. Когда вы обращаетесь к единственному человеку так, как будто его здесь несколько, то есть на "вы" – это уже абсолютно достаточное проявление вежливости!
Я не сильно разбираюсь в математике. И вот что меня смутило (x^∆х-1)/∆х) — здесь x, это не тот же самый x, что в 2^x или 3^x. Может быть его другой буквой лучше обозначить: (a^∆х-1)/∆х). Или я не прав?
И вывести, и доказать это можно через разложение в степенной ряд. Но в школе этому почему-то не учат.
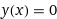
Почему производная экспоненты равна ей самой?