Представьте себе листок бумаги в клетку. Подозреваю, что уже на этом этапе некоторые хабралюди догадались, о чем пойдет речь. Что ж, моё почтение им. Остальные же продолжают представлять себе листок бумаги в клетку. Во всех подробностях. В мельчайших деталях.
А теперь представьте, что на этом простом листочке мы создадим простой, но оттого не менее впечатляющий симулятор жизни. Ни больше, ни меньше. Конечно, он будет очень упрощенный, но ведь чтобы понять что-то сложное надо начать с простого, не так ли? Этот симулятор можно применить ко множеству наук и с каждой из них он будет иметь множество достаточно интересных точек соприкосновения. От социологии до астрономии, от биологии до электротехники.
Ладно, хватит завлекалок. Пора удариться в математику.

Когда-то давно, в 1940-х годах, небезызвестный Джон фон Нейман задался целью спроектировать машину, которая может воспроизводить саму себя. Как ни странно, но ему это удалось. Правда правила этой машины были так сложны, что широкого распространения она не получила.
Спустя 30 лет другой ученый по имени Джон Конвей (да, Джон — очень популярное имя) заинтересовался этой машиной и решил её упростить. Как это снова ни странно, но и ему это удалось. Талантливые ученые, что и говорить.
И так. Снова по-быстрому рисуем у себя в голове бумагу с клетками. Правила очень простые:
Простой пример эволюции пяти вариантов триплетов (фигур из трех клеток):

Ничего сложного, не так ли? По большому счету, от игрока зависит только начальное расположение живых клеток, после чего они будут жить самостоятельно, а создателю останется за ними только следить. Но тут-то и возникает та самая причина, по которой этой игрой интересуются уже почти 40 лет.
Просто представьте себе количество вариантов расстановки клеток на минимальном поле, пусть хотя бы 10*10 клеток. Это 2100. И каждый из этих вариантов будет развиваться. Какой-то — всего несколько десятков ходов, а какой-то может зациклиться. Что уж тогда говорить о больших полях типа 100*100 или тем более о замкнутых по принципу тора.
В ходе полевых испытаний этой игры, сначала на бумаге, а затем и с помощью компьютерного моделирования было выявлено множество фигур, которые по их поведению можно рассортировать по нескольким классам.
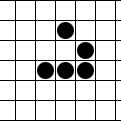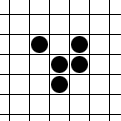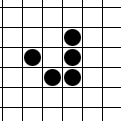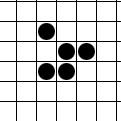
Самым простым примером двигающейся фигуры является Глайдер (планер):
Неинтересно?
Тогда взгляните на ружьё:
В таком виде, при небольшом отдалении, когда границы между клетками смазываются, эта анимация уже напоминает нечто биологическое, не так ли? Между прочим, ружье «стреляет» теми самыми глайдерами.
Прежде чем я дам вам возможность самим попробовать составлять фигуры, позвольте сказать пару слов о пользе всей этой фигни для науки.
Вообще, если говорить научными терминами, то эта игра является дискретной динамической системой, поведение которой полностью определяется в терминах локальных зависимостей, а короче говоря — клеточным автоматом. То есть решетка, в которой каждая ячейка имеет конечное число состояний, а само это состояние определяется через жестко заданные правила перехода.
Данная игра являет собой едва ли не простейший клеточный автомат. А представьте себе, что каждая клетка имеет не два, а с десяток разных состояний, и их изменения зависят не только от соседних 8-ми клеток, но и от 16-ти на «втором периметре».
Такие клеточные автоматы — это один из самых простых примеров того, что иногда называют «самоорганизованные системы». Эта предметная область привлекла внимание ученых и математиков из различных областей. В ней изучается построение сложных структур и форм поведения на основе очень простых правил. Например, появление лепестков роз или полос на зебре из растущих рядом клеток. Поэтому изучение конечных автоматов может привести к совершенно неожиданным результатам в абсолютно разных науках. Так, например, эволюции некоторых сложных колоний удивительным образом схематично повторяют этапы развития спиралевидных галактик. Равно как они во многом совпадают с законами поведения популяций примитивных организмов.
Ну а теперь настало время самим попробовать это в деле.
Вперед на испытания. И да пребудет с вами random ))
А теперь представьте, что на этом простом листочке мы создадим простой, но оттого не менее впечатляющий симулятор жизни. Ни больше, ни меньше. Конечно, он будет очень упрощенный, но ведь чтобы понять что-то сложное надо начать с простого, не так ли? Этот симулятор можно применить ко множеству наук и с каждой из них он будет иметь множество достаточно интересных точек соприкосновения. От социологии до астрономии, от биологии до электротехники.
Ладно, хватит завлекалок. Пора удариться в математику.

Когда-то давно, в 1940-х годах, небезызвестный Джон фон Нейман задался целью спроектировать машину, которая может воспроизводить саму себя. Как ни странно, но ему это удалось. Правда правила этой машины были так сложны, что широкого распространения она не получила.
Спустя 30 лет другой ученый по имени Джон Конвей (да, Джон — очень популярное имя) заинтересовался этой машиной и решил её упростить. Как это снова ни странно, но и ему это удалось. Талантливые ученые, что и говорить.
Правила
И так. Снова по-быстрому рисуем у себя в голове бумагу с клетками. Правила очень простые:
- Каждая клетка может находиться в одном из двух состояний: живая (заполненная) или мёртвая (пустая).
- Каждый ход у каждой клетки определяется ее состояние и состояние всех её 8-ми соседей.
- Если это пустая клетка и соседей ровно 3, то эта клетка оживает. Во всех остальных случаях пустая клетка остается пустой.
- Если же это живая клетка, то подсчитывается количество живых соседей.
- Если соседей 0 или 1, то клетка умирает от одиночества.
- Если соседей 2 или 3, то клетка продолжает жить.
- Если соседей 4 или больше, то клетка умирает от перенаселения.
Простой пример эволюции пяти вариантов триплетов (фигур из трех клеток):

Ничего сложного, не так ли? По большому счету, от игрока зависит только начальное расположение живых клеток, после чего они будут жить самостоятельно, а создателю останется за ними только следить. Но тут-то и возникает та самая причина, по которой этой игрой интересуются уже почти 40 лет.
Просто представьте себе количество вариантов расстановки клеток на минимальном поле, пусть хотя бы 10*10 клеток. Это 2100. И каждый из этих вариантов будет развиваться. Какой-то — всего несколько десятков ходов, а какой-то может зациклиться. Что уж тогда говорить о больших полях типа 100*100 или тем более о замкнутых по принципу тора.

Фигуры
В ходе полевых испытаний этой игры, сначала на бумаге, а затем и с помощью компьютерного моделирования было выявлено множество фигур, которые по их поведению можно рассортировать по нескольким классам.
- Устойчивые фигуры: фигуры, которые остаются неизменными
- Периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений
- Двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением
- Ружья: фигуры, у которых состояние повторяется, но дополнительно появляется двигающаяся фигура
- Паровозы: двигающиеся фигуры, которые оставляют за собой следы в виде устойчивых или периодических фигур
- Пожиратели: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами
Самым простым примером двигающейся фигуры является Глайдер (планер):

Неинтересно?
Тогда взгляните на ружьё:
В таком виде, при небольшом отдалении, когда границы между клетками смазываются, эта анимация уже напоминает нечто биологическое, не так ли? Между прочим, ружье «стреляет» теми самыми глайдерами.
Интерес для науки
Прежде чем я дам вам возможность самим попробовать составлять фигуры, позвольте сказать пару слов о пользе всей этой фигни для науки.
Вообще, если говорить научными терминами, то эта игра является дискретной динамической системой, поведение которой полностью определяется в терминах локальных зависимостей, а короче говоря — клеточным автоматом. То есть решетка, в которой каждая ячейка имеет конечное число состояний, а само это состояние определяется через жестко заданные правила перехода.
Данная игра являет собой едва ли не простейший клеточный автомат. А представьте себе, что каждая клетка имеет не два, а с десяток разных состояний, и их изменения зависят не только от соседних 8-ми клеток, но и от 16-ти на «втором периметре».
Такие клеточные автоматы — это один из самых простых примеров того, что иногда называют «самоорганизованные системы». Эта предметная область привлекла внимание ученых и математиков из различных областей. В ней изучается построение сложных структур и форм поведения на основе очень простых правил. Например, появление лепестков роз или полос на зебре из растущих рядом клеток. Поэтому изучение конечных автоматов может привести к совершенно неожиданным результатам в абсолютно разных науках. Так, например, эволюции некоторых сложных колоний удивительным образом схематично повторяют этапы развития спиралевидных галактик. Равно как они во многом совпадают с законами поведения популяций примитивных организмов.
Практика
Ну а теперь настало время самим попробовать это в деле.
- Здесь можно и нужно почитать про «жизнь» подробнее. Тут описано множество фигур и принципов. Да и вообще много полезного.
- Здесь можно поиграть в «жизнь» на флэше. Настроек никаких нет. Всё упрощено до минимума. Чисто для ознакомления.
- Здесь же можно скачать программу-эмулятор с расширенными возможностями. Регулировка скорости времени. Возможность сохранения и загрузки начальных конфигураций. Изменяемый масштаб поля. В общем, полная свобода действий. Для хардкорщиков. К сожалению, только под Windows.
- Ну а здесь лежит подобный эмулятор для всех платформ (Windows (2000+), Mac OS X (10.3.9+) and Linux (GTK+)). Его я сам не запускал, но судя по описанию, возможностей у него не меньше, чем у предыдущей программы.
Вперед на испытания. И да пребудет с вами random ))