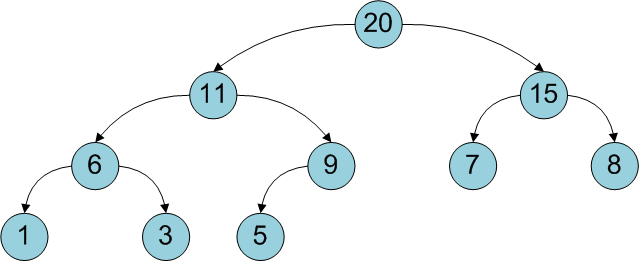
Я расскажу о структуре под названием дерево отрезков и приведу его простую реализацию на языке С++. Эта структура весьма полезна в случаях, когда необходимо часто искать значение какой-то функции на отрезках линейного массива и иметь возможность быстро изменять значения группы подряд идущих элементов.
Типичный пример задачи на дерево отрезков:
Есть линейный массив, изначально заполненный некоторыми данными. Далее приходят 2 типа запросов:
1й тип — найти значение максимального элемента на отрезке массива [a..b].
2й тип — заменить iй элемент массива на x.
Возможен запрос «добавить х ко всем элементам на отрезке [a..b]», но в данной статье я его не рассматриваю.
С помощью дерева отрезков можно искать не только максимум чисел, но и любую функцию, удовлетворяющую свойству ассоциативности.
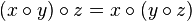
Это ограничение связано с тем, что используется предпросчет значений для некоторых отрезков.
Типичный пример задачи на дерево отрезков:
Есть линейный массив, изначально заполненный некоторыми данными. Далее приходят 2 типа запросов:
1й тип — найти значение максимального элемента на отрезке массива [a..b].
2й тип — заменить iй элемент массива на x.
Возможен запрос «добавить х ко всем элементам на отрезке [a..b]», но в данной статье я его не рассматриваю.
С помощью дерева отрезков можно искать не только максимум чисел, но и любую функцию, удовлетворяющую свойству ассоциативности.
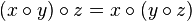
Это ограничение связано с тем, что используется предпросчет значений для некоторых отрезков.
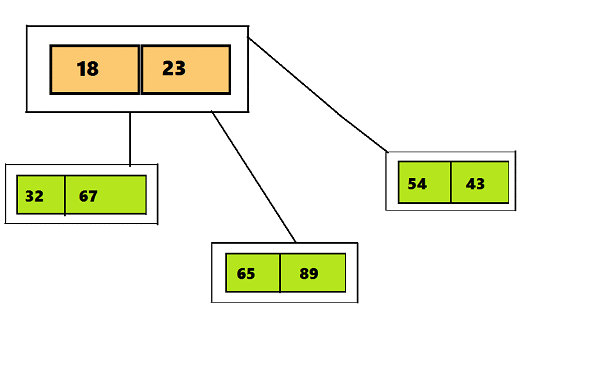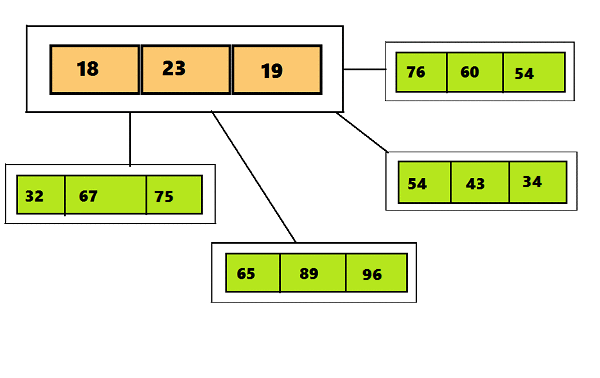
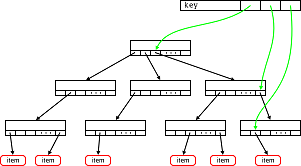 Этот топик повествует об использовании Radix Tree на практическом примере.
Этот топик повествует об использовании Radix Tree на практическом примере.