Иногда мне в голову попадают задачи, не имеющие какой-то очевидной практической ценности, но, тем не менее, они захватывают так или иначе мое воображение, по крайней мере, пока не решу. Практическая ценность задачи, как правило, нулевая, но в процессе решаются другие, которые могут иметь бОльшую ценность, чем решенная.
Все началось с желания изучить свойства правильных октагонов и октаграмм, но результаты оказались применимы ко всем выпуклым многоугольникам (полигонам) и звездам, построенным в них (по аналогии назову их полиграммами — пентаграмма, гексаграмма, септаграмма, октаграмма и т.д. — хотя этот термин имеет и иные значения).
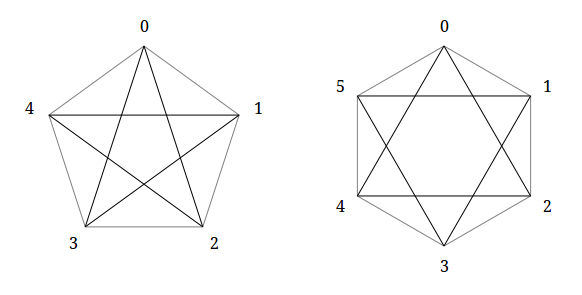
Для начала терминология. Пентаграммой называют совокупность всех диагоналей пятиугольника, в случае гексаграммы — это уже не все диагонали, а только те, которые соединяют непротивоположные вершины шестиугольника. Во обоих случаях эти вершины идут через одну друг от друга. Например, если вершины пятиугольника перенумеровать(0, 1, 2, 3, 4) , то пентаграмма — совокупность линий (0, 2) , (1, 3) , (2, 4) , (3, 0) , (4, 1) . Гексаграмма (0, 1, 2, 3, 4, 5) , соответственно, является совокупностью линий (0, 2) , (1, 3) , (2, 4) , (3, 5) , (4, 0) , (5, 1) . Нули в качестве начальной точки взяты не случайно и не как дань програмистскому мышлению, удобство этого обозначения я опишу ниже. Линии, образующие полиграмму, я буду называть ребрами. Вершинами полиграммы я буду называть вершины исходного полигона, а не все точки пересечения ребер.
Все началось с желания изучить свойства правильных октагонов и октаграмм, но результаты оказались применимы ко всем выпуклым многоугольникам (полигонам) и звездам, построенным в них (по аналогии назову их полиграммами — пентаграмма, гексаграмма, септаграмма, октаграмма и т.д. — хотя этот термин имеет и иные значения).
Для начала терминология. Пентаграммой называют совокупность всех диагоналей пятиугольника, в случае гексаграммы — это уже не все диагонали, а только те, которые соединяют непротивоположные вершины шестиугольника. Во обоих случаях эти вершины идут через одну друг от друга. Например, если вершины пятиугольника перенумеровать
