Sqrt-декомпозиция — это метод, или структура данных, позволяющая в режиме онлайн проводить такие операции, как подсчет суммы на отрезке за  и обновление элемента за
и обновление элемента за  . Существуют более эффективные структуры, такие как дерево фенвика или дерево отрезков, которые оба запроса обрабатывают за
. Существуют более эффективные структуры, такие как дерево фенвика или дерево отрезков, которые оба запроса обрабатывают за 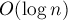 . Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.
. Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.
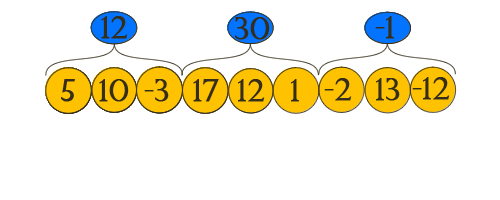
Пусть нам задан массив A[i], на который поступают запросы вида:
Мы можем предрасчитать массив частичных сумм, а именно: . Однако на запрос изменения, потребует пересчета частичных сумм (содержащих этот элемент) и в худшем случае составит асимптотику порядка
. Однако на запрос изменения, потребует пересчета частичных сумм (содержащих этот элемент) и в худшем случае составит асимптотику порядка 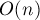 , что не есть хорошо.
, что не есть хорошо.
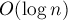 . Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.
. Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа. 
Постановка задачи
Пусть нам задан массив A[i], на который поступают запросы вида:
- посчитать сумму на отрезке [L; R] (позже, мы поймем, что аналогично можно вычислять функции min, max, gcd и др.
- добавить к элементу A[i], delta
Наивная реализация
Мы можем предрасчитать массив частичных сумм, а именно:
for(int j = 0; j < i; j++) B[j] += A[i];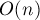 , что не есть хорошо.
, что не есть хорошо.