 Этот топик повествует об использовании Radix Tree на практическом примере. Radix Tree или дерево остатков — это структура данных, формируемая по принципу хранение значений в листовом узле. Промежуточные узлы представляют собой элемент конечного значения. Это может быть бит для чисел, символ для строк или цифра для номера, как в примере ниже. Приведенный алгоритм сжатия с использованием Radix Tree используется в реальной embeded системе, для хранения параметров телефонного файрвола.
Этот топик повествует об использовании Radix Tree на практическом примере. Radix Tree или дерево остатков — это структура данных, формируемая по принципу хранение значений в листовом узле. Промежуточные узлы представляют собой элемент конечного значения. Это может быть бит для чисел, символ для строк или цифра для номера, как в примере ниже. Приведенный алгоритм сжатия с использованием Radix Tree используется в реальной embeded системе, для хранения параметров телефонного файрвола.Техническое задание
Итак исходные данные.
Допустим у нас имеется телефонная книга, или проще говоря список контактов. С каждым контактом
связан набор атрибутов. Для программы «телефонный firewall» — это могут быть булевы атрибуты:
исходящий/входящий звонок, работа в рабочее/не рабочее время, разрешить/блокировать или автоответ
при звонке. Задача состоит в хранении списка контанктов и их атрибутов в памяти телефона, в сжатой форме. В условиях ограниченного объема доступной памяти.
Итак, более детализированное техническое задание выглядит таким образом:
— Имеется .INI файл с набором правил для каждого номера. Правило содержит телефонный номер
и собственно булевые атрибуты, применимые к нему. Номера уникальны.
Пример .INI файла, где 12345 — номер телефона:
[RULES]
R0000=12345,0,0,0,0,0,0,0,0,0,0
R0001=123764465,0,0,0,0,1,0,1,0,0,0
…
R0765=…
— Внутренее представление правила:
class NumberEntry
{
string number ;
bool attCalledNumber ;
bool attCallingNumber ;
bool attInboundCall ;
bool attOutboundCall ;
bool attWorkingHours ;
bool attNonWorkingHours ;
bool attBlocked ;
bool attAllowed ;
bool attPrefix ;
bool attAutoAnswer ;
};
* This source code was highlighted with Source Code Highlighter.— Для имеющегося набора правил, следует построить промежуточный расширенный граф.
В Графе, каждый узел может быть помечен как листовой. Для примера возьмем такой набор гипоптетических номеров:
012345
012346
01234567#
54647
5463
54638
Должен быть построен промежуточный граф:

Рисунок 1. Расширенный (не сжатый) граф из ТЗ.
— Расширенный Граф строится по следующим правилам:
Последняя цифра каждого номера в списке, обозначает листовой узел. Атрибуты связанные с номером откносяться только к листовому узлу. В графе, любой узел может быть помечен, как листовой. Для примера выше, цифра 5 в номере 012345 представляет листовой узел, несмотря на то, что также является частью номера 01234567#
— После того, как все номера добавлены в промежуточный граф (Expanded), следует его сжать. Таким образом, чтобы каждый узел промежуточного графа
(наример 0xxx5xxx#), заменяется последовательностью компактных узлов (Compact Nodes, без 'x').
Узлы расширенного и компактного графа представлены такими струтурами:
#pragma pack(push, 1) // выравнивание структуры в 1 байт для MS C++
#define K_MAX_EXPANDED_NODES 12 // максимальное цифр в узле. Это цифры 0-9, * и #
struct SG_Y_DigitElement // Узел промежуточного графа, 4 байта
{
UINT digit : 4; // Цифра 0-9 . '*' задана как 0xA, '#' как 0xB. Всего 12 значений, поэтому 4 бита
UINT nextNodeOffset : 13; // Адрес следующего узла графа, относительно первого байта графа
BOOL leafNode : 1; // Листовой узел?
BOOL attCalledNumber : 1; // Атрибуты. Заданы только у листового узла
BOOL attCallingNumber : 1;
BOOL attInboundCall : 1;
BOOL attOutboundCall : 1;
BOOL attWorkingHours : 1;
BOOL attNonWorkingHours : 1;
BOOL attBlocked : 1;
BOOL attAllowed : 1;
BOOL attPrefix : 1;
BOOL attAutoAnswer : 1;
BOOL attReserved1 : 1;
BOOL attReserved2 : 1;
BOOL attReserved3 : 1;
BOOL attReserved4 : 1;
}
typedef SG_Y_DigitElement SG_Y_ExpandedNode[K_MAX_EXPANDED_NODES];
struct SG_Y_CompactNode // сжатый узел размером 5 байт. Длинна последовательности+цифра
{
UINT8 nodeLen : 4;
UINT8 reserved : 4;
/* Первая цифра в последовательности */
SG_Y_DigitElement digits;
} ;
#pragma pack(pop)
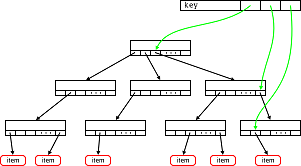
* This source code was highlighted with Source Code Highlighter.— На основе расширенного графа, который представлен массивом из элементов типа SG_Y_ExpandedNode, строится компактный граф с узлами типа SG_Y_CompactNode. Таким образом и происходит сжатие данных, путем удаления пустых элементов, обозначенных как 'x', из SG_Y_ExpandedNode. Для расширенного графа из примера выше, компактный граф будет иметь такой вид после сжатия (зеленым обозначено количество цифр в компактном узле, поле nodeLen структуры SG_Y_CompactNode):

Рисунок 2. Сжатый граф из ТЗ.
— Следует отметить, что указатели на узлы (поле nextNodeOffset в SG_Y_DigitElement), в обоих графах представляют собой индекс относительно первого байта графа. Оба графа представлены массивами.
— Подытожим ТЗ:
- На вход поступает .INI файл с правилами файрвола для телефонного номера.
- Считываем правила в список типа NumberEntry
- Формируем промежуточный расширенный граф на основе списка. Где листовой узел графа, содержит атрибуты относящиеся к номеру.
- Генерируем сжатый граф, путем удаления пустых элементов из расширенного
Построение промежуточного графа
Первый шаг алгоритма — тривиален. Будем считать, что правила считаны и добавлены в список. Имеем набор номеров в list, который поступает на вход генератору графа. Здесь и в прилагаемых исходниках, используется термин генератор графа (GraphGenerator), для обозначения класса реализуещего алгоритм построения и сжатия.
Переходим непосредственно к построению промежуточного расширенного графа (Expanded).
Обратите еще раз внимание, на рисунок 1. Этот промежуточный граф, можно представить бинарным деревом, построенным по принципу Radix Tree (или русский аналог — дерево остатков). Давайте более подрбно остановимся на этой структуре данных.
Добавление элемента в Radix Tree происходит следующим образом:
— Берется каждый i-ый бит добавляемого значения.
— Элемент проталкивается вниз дерева, на основе текущего бита. Если i-ый бит — 0, значит идем влево, иначе вправо.
И так до тех пор, пока не будут обработаны все значимые биты значения.
— В итоге, листовой узел Radix Tree — будет обозначать само значение. Таким образом, проходя путь от корня к листовому узлу,
получаем все биты значения. Иллюстрацию подхода можно найти здесь. В русской wiki описания Radix Tree еще нет.
Для примера возьмем три номера: 0123, 01234, 123. Тогда на первой итерации, дерево построится сверху вниз, создав 4 узла (0,1,2,3-лист). На второй итерации, при добавлении номера 01234, мы пройдем по тому-же пути при добавлении элементов 0, 1, 2 и 3, так как узлы для этих цифр уже созданы. А вот при добавлении последнего элемента, находясь в узле со значением 3, мы создаем новый листовой узел 4. И на третей итерации, добавление номера 123, происходит вправую сторону.
Если представить полученное дерево в виде графа, где узел справа является «братом», а узел слева «сыном», то получим такую картину
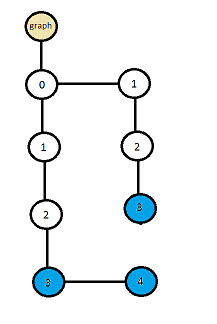
Рисунок 3. Связи графа
Применим алгоритм добавления в Radix Tree для нашего расширенного графа. Узел графа представлен массивом из 12-ти возможных значений (0-9*#). То есть мы применяем отображение expandedNode[digit], для проверки и задания значения узла.
На рисунке ниже, expandedGraph — представлен в виде массива узлов expandedNode. '-' обозначает пустой элемент, голубой элемент — обозначает листовой узел. Напомню, листовой узел в нашей задаче содержит атрибуты номера.
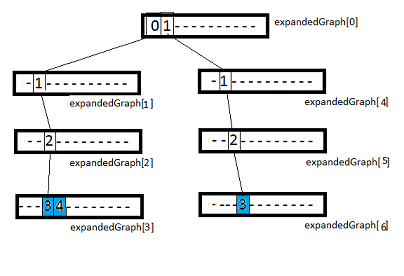
Рисунок 4. Расширенный (несжатый) граф
Думаю идея использования Radix Tree становится уже более ясной и из самого рисунка понятно, что сжатие можно произвести путем удаления пустых элементов.
Сжатие. Построение компактного графа.
Алгоритм сжатия относительно прост, и может быть описан в двух предложениях. Имеем расширенный граф expandedGraph, представленный в виде массива из expandedNode.
— Берем непустые элементы (цифры) из узла expandedGraph[i]. Переносим их в сжатый граф, который представлен массивом из SG_Y_CompactNode. Задаем длину компактного узла как количество непустых элементов.
— Применяем процедуру сжатия для каждого дочернего узла. Меняем ссылки на дочерние элементы относительно начала CompactGraph.
Алгоритм сжатия — рекурсивный. Мы выбираем непустые элементы из узла, и выкладываем их последовательно в сжатом графе, задавая длину узла. Таким образом из расширенного узла вида
«01-----------», мы получаем компактный узел '[2]01', где [2] — длина узла.
Рекурсивно вызываем процедуру для дочерних элементов '0' и '1'. Затем связываем '0' и '1' с дочерними элементами относительно начала сжатого графа.

Рисунок 5. Результат — сжатый граф.
Заключение.
— Использование алгоритма оптимально подходит для сжатия и хранения телефонных номеров. Префиксы вроде кодов сотовых операторов, кода страны или города, повзоляет хранить эти самые кода в корневых узлах графа. Реализация непосредственно используется в софте крупной телекоммуникационной компании.
Однако, его можно использовать для любых последовательностей данных. Например для хранения символьных данных латиницы без учета регистра, размер узла графа нужно увеличить до 26-ти элементов. Соответственно и под поле digit выделить 5 бит.
Если атрибуты не требуются, то размер SG_Y_DigitElement можно уменьшить вплоть до 2-х байт. Например 5 бит для значения символа, 10 бит для указателя на следующий узел и 1 бит для маркера листа.
Очевидно, что ограничения на количество адресуемых записей ограничено полем nextNodeOffset. В нашем примере 13 бит, достаточно для адресации 8192 записи.
Здесь реализация алгоритма