
Привет, %username%!
Многим известно, что стандартом по умолчанию в области симметричного шифрования долгое время считался алгоритм DES. Первая успешная атака на этот неубиваемый алгоритм была опубликована в 1993 году, спустя 16 лет после принятия его в качестве стандарта. Метод, который автор назвал линейным криптоанализом, при наличии 247 пар открытых/зашифрованных текстов, позволяет вскрыть секретный ключ шифра DES за 243 операций.
Под катом я попытаюсь кратко изложить основные моменты этой атаки.
Линейный криптоанализ
Линейный криптоанализ — особый род атаки на симметричные шифры, направленный на восстановление неизвестного ключа шифрования, по известным открытым сообщениям и соответствующим им шифртекстам.
В общем случае атака на основе линейного криптоанализа сводится к следующим условиям. Злоумышленник обладает большим количеством пар открытый/зашифрованный текст, полученных с использованием одного и того же ключа шифрования K. Цель атакующего восстановить частично или полностью ключ K.
В первую очередь злоумышленник производит исследование шифра и находит т.н. статистический аналог, т.е. уравнение следующего вида, выполняющееся с вероятностью P ≠ 1/2 для произвольной пары открытый/закрытый текст и фиксированного ключа:
PI1 ⊕ PI2 ⊕… ⊕ PIa ⊕ CI1 ⊕ CI2 ⊕… ⊕ CIb = KI1 ⊕ KI2 ⊕… ⊕ KIc (1),
где Pn, Cn, Kn — n-ые биты текста, шифртекста и ключа.
После того как подобное уравнение будет найдено атакующий может восстановить 1 бит информации о ключе, используя следующий алгоритм
Алгоритм 1
Пусть T — количество текстов, для которых левая часть уравнения (1) равняется 0, тогда
Если T>N/2, где N — число известных открытых текстов.
Предположить, что KI1 ⊕ KI2 ⊕… ⊕ KIc = 0 (когда P>1/2) или 1 (когда P<1/2).
Иначе
Предположить, что KI1 ⊕ KI2 ⊕… ⊕ KIc = 1 (когда P>1/2) или 0 (когда P<1/2).
Очевидно, что успех алгоритма напрямую зависит от значения |P-1/2| и от количества доступных пар открытый/закрытый текст N. Чем больше вероятность P равенства (1) отличается от 1/2, тем меньше количество открытых текстов N необходимо для атаки.
Возникают две проблемы, которые необходимо решить для успешной реализации атаки:
- Как найти эффективное уравнение вида (1).
- Как с помощью такого уравнения получить больше одного бита информации о ключе.
Рассмотрим решение этих вопросов на примере шифра DES.
Описание DES
Но для начала кратко опишем работу алгоритма. О DES сказано уже достаточно. Полное описание шифра можно найти на Википедии. Однако для дальнейшего объяснения атаки нам потребуется ряд определений которые лучше ввести заранее.
Итак, DES это блочный шифр, основанный на сети Фейстеля. Шифр имеет размер блока 64 бита и размер ключа 56 бит. Рассмотрим схему шифрования алгоритма DES.
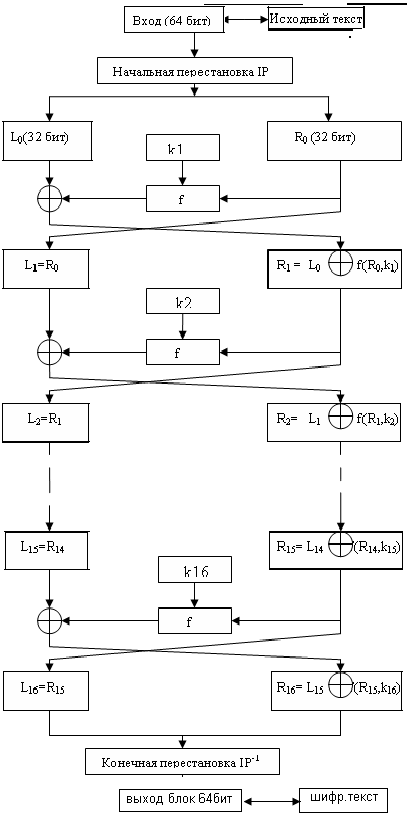
Как видно из рисунка, при шифровании над текстом производятся следующие операции:
- Начальная перестановка бит. На этом этапе биты входного блока перемешиваются в определенном порядке.
- После этого перемешанные биты разбиваются на две половины, которые поступают на вход функции Фейстеля. Для стандартного DES сеть Фейстеля включает 16 раундов, но существуют и другие варианты алгоритма.
- Два блока, полученных на последнем раунде преобразования объединяются и над полученным блоком производится еще одна перестановка.
На каждом раунде сети Фейстеля 32 младших бита сообщения проходят через функцию f:
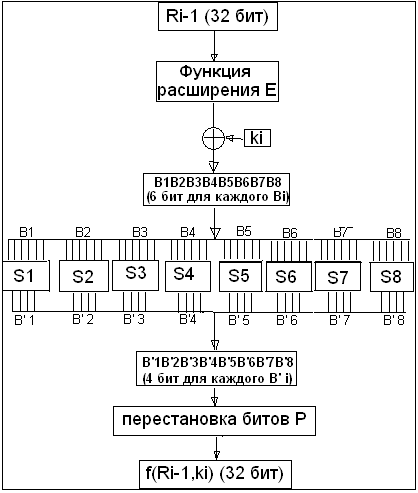
Рассмотрим операции, выполняющиеся на этом этапе:
- Входной блок проходит через функцию расширения E, которая преобразует 32-битный блок в блок длиной 48 бит.
- Полученный блок складывается с раундовым ключом Ki.
- Результат предыдущего шага разбивается на 8 блоков по 6 бит каждый.
- Каждый из полученных блоков Bi проходит через функцию подстановки S-Boxi, которая заменяет 6-битную последовательность, 4-битным блоком.
- Полученный в результате 32-битный блок проходит через перестановку P и возвращается в качестве результата функции f.
Наибольший интерес, с точки зрения криптоанализа шифра, для нас представляют S блоки, предназначенные для скрытия связи между входными и выходными данными функции f. Для успешной атаки на DES мы сперва построим статистические аналоги для каждого из S-блоков, а затем распространим их на весь шифр.
Анализ S блоков
Каждый S-блок принимает на вход 6-битную последовательность, и для каждой такой последовательности возвращается фиксированное 4-битное значение. Т.е. имеется всего 64 варианта входных и выходных данных. Наша задача показать взаимосвязь между входными и выходными данными S блоков. К примеру, для третьего S-блока шифра DES, 3-й бит входной последовательности равен 3-му биту выходной последовательности в 38 случаях из 64. Следовательно, мы нашли следующий статистический аналог для третьего S-блока:
S3(x)[3] = x[3], который выполняется с вероятность P=38/64.
Обе части уравнения представляют 1 бит информации. Поэтому в случае если бы левая и правая части были независимы друг от друга, уравнение должно было бы выполняться с вероятностью равной 1/2. Таким образом, мы только что продемонстрировали связь между входными и выходными данными 3-го S-блока алгоритма DES.
Рассмотрим как можно найти статистический аналог S-блока в общем случае.
Для S-блока Sa, 1 ≤ α ≤ 63 и 1 ≤ β ≤ 15, значение NSa(α, β) описывает сколько раз из 64 возможных XOR входных бит Sa наложенных на биты α равны XOR выходных бит, наложенных на биты β, т.е.:
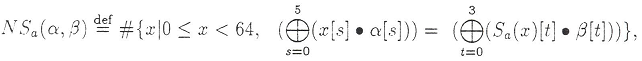 где символ • — логическое И.
где символ • — логическое И.Значения α и β, для которых NSa(α, β) сильнее всего отличается от 32, описывают самый эффективный статистический аналог S-блока Sa.
Наиболее эффективный аналог был найден в 5-ом S-блоке шифра DES для α = 16 и β = 15 NS5(16, 15)=12. Это значит, что справедливо следующее уравнение: Z[2]=Y[1] ⊕ Y[2] ⊕ Y[3] ⊕ Y[4], где Z — входная последовательность S-блока, а Y — выходная последовательность.
Или с учетом того, что в алгоритме DES перед входом в S-блок данные складываются по модулю 2 с раундовым ключом, т.е. Z[2] = X[2] ⊕ K[2] получаем
X[2] ⊕ Y[1] ⊕ Y[2] ⊕ Y[3] ⊕ Y[4] = K[2], где X и Y — входные и выходные данные функции f без учета перестановок.
Полученное уравнение выполняется на всех раундах алгоритма DES с одинаковой вероятностью P=12/64.
На следующей таблице приведен список эффективных, т.е. имеющих наибольшее отклонение от P=1/2, статистических аналогов для каждого s-блока алгоритма DES.
Построение статистических аналогов для нескольких раундов DES
Покажем теперь каким образом можно объединить статистические аналоги нескольких раундов DES и в итоге получить статистический аналог для всего шифра.
Для этого рассмотрим трехраундовую версию алгоритма:
Применим эффективный статистический аналог 5-го s-блока для вычисления определенных бит значения X(2).
Мы знаем что с вероятностью 12/64 в f-функции выполняется равенство X[2] ⊕ Y[1] ⊕ Y[2] ⊕ Y[3] ⊕ Y[4] = K[2], где X[2] — второй входной бит 5-го S-блока, он по сути является 26-м битом последовательности, полученной после расширения входных бит. Анализируя функцию расширения можно установить что на месте 26 бита оказывается 17-й бит последовательности X(1).
Аналогичным образом, Y[1],…, Y[4] по сути являются 17-м, 18-м, 19-м и 20-м битом последовательности полученной до перестановки P. Исследовав перестановку P, получаем что биты Y[1],…, Y[4] на самом деле являются битами Y(1)[3], Y(1)[8], Y(1)[14], Y(1)[25].
Бит ключа K[2] вовлеченный в уравнения является 26 битом подключа первого раунда K1 и тогда статистический аналог приобретает следующую форму:
X(1)[17] ⊕ Y(1)[3] ⊕ Y(1)[8] ⊕ Y1[14] ⊕ Y(1)[25] = K1[26].
Следовательно, X(1)[17] ⊕ K1[26] = Y(1)[3] ⊕ Y(1)[8] ⊕ Y(1)[14] ⊕ Y(1)[25] (2) с вероятностью P=12/64.
Зная 3, 8, 14, 25 биты последовательности Y(1) можно найти 3, 8, 14, 25 биты последовательности X(2):
X(2)[3] ⊕ X(2)[8] ⊕ X(2)[14] ⊕ X(2)[25] = PL[3] ⊕ PL[8] ⊕ PL[14] ⊕ PL[25] ⊕ Y(1)[3] ⊕ Y(1)[8] ⊕ Y(1)[14] ⊕ Y(1)[25] или с учетом уравнения (2)
X(2)[3] ⊕ X(2)[8] ⊕ X(2)[14] ⊕ X(2)[25] = PL[3] ⊕ PL[8] ⊕ PL[14] ⊕ PL[25] ⊕ X(1)[17] ⊕ K1[26] (3) с вероятностью 12/64.
Найдем подобное выражение используя последний раунд. На этот раз мы имеем уравнение
X(3)[17] ⊕ K3[26] = Y(3)[3] ⊕ Y(3)[8] ⊕ Y(3)[14] ⊕ Y(3)[25].
Так как
X(2)[3] ⊕ X(2)[8] ⊕ X(2)[14] ⊕ X(2)[25] = СL[3] ⊕ СL[8] ⊕ СL[14] ⊕ СL[25] ⊕ Y(3)[3] ⊕ Y(3)[8] ⊕ Y(3)[14] ⊕ Y(3)[25]
получаем, что
X(2)[3] ⊕ X(2)[8] ⊕ X(2)[14] ⊕ X(2)[25] = СL[3] ⊕ СL[8] ⊕ СL[14] ⊕ СL[25] ⊕ X(3)[17] ⊕ K3[26] (4) с вероятностью 12/64.
Приравняв правые части уравнений (3) и (4) получаем
СL[3] ⊕ СL[8] ⊕ СL[14] ⊕ СL[25] ⊕ X(3)[17] ⊕ K3[26] = PL[3] ⊕ PL[8] ⊕ PL[14] ⊕ PL[25] ⊕ X(1)[17] ⊕ K1[26] с вероятностью (12/64)2+(1-12/64)2.
С учетом того, что X(1) = PR и X(3) = CR получаем статистический аналог
СL[3, 8, 14, 25] ⊕ CR[17] ⊕ PL[3, 8, 14, 25] ⊕ PR[17] = K1[26] ⊕ K3[26] (5),
который выполняется с вероятностью (12/64)2+(1-12/64)2=0.7.
Описанный выше статистический аналог можно представить графически следующим образом (биты на рисунке пронумерованы справа налево и начиная с нуля):

Все биты в левой части уравнения известны атакующему, следовательно он может применить алгоритм 1 и узнать значение K1[17] ⊕ K3[17]. Покажем как с помощью данного статистического аналога можно вскрыть не 1, а 12 бит ключа шифрования K.
Атака на DES с известным открытым текстом
Приведем способ с помощью которого можно расширить атаку и получить сразу 6 бит подключа первого раунда.
Составляя уравнение (5) мы принимали во внимание тот факт, что нам неизвестно значение F1(PR, K1)[3, 8, 14, 25]. Поэтому мы использовали его статистический аналог K1[26] ⊕ PR[17].
Вернем вместо выражения K1[26] ⊕ PR[17] значение F1(PR, K1)[3, 8, 14, 25] и получим следующее уравнение:
СL[3, 8, 14, 25] ⊕ CR[17] ⊕ PL[3, 8, 14, 25] ⊕ F1(PR, K1)[3, 8, 14, 25] = K3[26] (6), которое будет выполняться с вероятностью 12/64. Вероятность изменилась так как мы оставили только статистический аналог из третьего раунда, все остальные значения фиксированы.
Выше мы уже определили, что на значение F1(PR, K1)[3, 8, 14, 25] оказывают влияние входные биты 5-го S-блока, а именно биты ключа K1[25~30] и биты блока PR[16~21]. Покажем каким образом обладая только набором открытых/закрытых текстов можно восстановить значение K1[25~30]. Для этого воспользуемся алгоритмом 2.
Алгоритм 2
Пусть N — количество известных перед атакой пар открытый/закрытый текст. Тогда для вскрытия ключа необходимо проделать следующие шаги.
For (i=0; i<64; i++) do
{
For(j=0; j<N; j++) do
{
if(СLj[3, 8, 14, 25] ⊕ CRj[17] ⊕ PLj[3, 8, 14, 25] ⊕ F1(PRj, i)[3, 8, 14, 25]=0) then
Ti=Ti+1
}
}
В качестве вероятной последовательности K1[25~30] принимается такое значение i, при котором выражение |Ti-N/2| имеет максимальное значение.
При достаточном количестве известных открытых текстов алгоритм будет с большой вероятностью возвращать корректное значение шести бит подключа первого раунда K1[25~30]. Объясняется это тем, что в случае если переменная i не равна K1[25~30], тогда значение функции F1(PRj, K)[3, 8, 14, 25] будет случайным и количество уравнений для такого значения i, при котором левая часть равна нулю будет стремиться к N/2. В случае же если подключ угадан верно, левая часть будет с вероятностью 12/64 равна фиксированному биту K3[26]. Т.е. будет наблюдаться значительное отклонение от N/2.
Получив 6 бит подключа K1, можно аналогичным образом вскрыть 6 бит подключа K3. Все что для этого нужно, это заменить в уравнении (6) C на P и K1 на K3:
PL[3, 8, 14, 25] ⊕ PR[17] ⊕ CL[3, 8, 14, 25] ⊕ F3(CR, K3)[3, 8, 14, 25] = K1[26].
Алгоритм 2 возвратит корректное значение K3[25~30] потому что процесс расшифровки алгоритма DES идентичен процессу шифрования, просто последовательность ключей меняется местами. Так на первом раунде расшифрования используется ключ K3, а на последнем ключ K1.
Получив по 6 бит подключей K1 и K3 злоумышленник восстанавливает 12 бит общего ключа шифра K, т.к. раундовые ключи являются обычной перестановкой ключа K. Количество открытых текстов необходимых для успешной атаки зависит от вероятности статистического аналога. Для вскрытия 12 бит ключа 3-раундового DES достаточно 100 пар открытых/закрытых текстов. Для вскрытия 12 бит ключа 16-раундового DES потребуется порядка 244 пар текстов. Остальные 44 бита ключа вскрываются обычным перебором.
Ссылки
Mitsuru Matsui — Linear cryptanalysis method of DES cipher
Tutorial on Linear and Differential Cryptanalysis