В этой статье я познакомлю вас с концепцией параллельной сортировки. Мы обсудим теорию и реализацию шейдера, сортирующего пиксели.
GIF
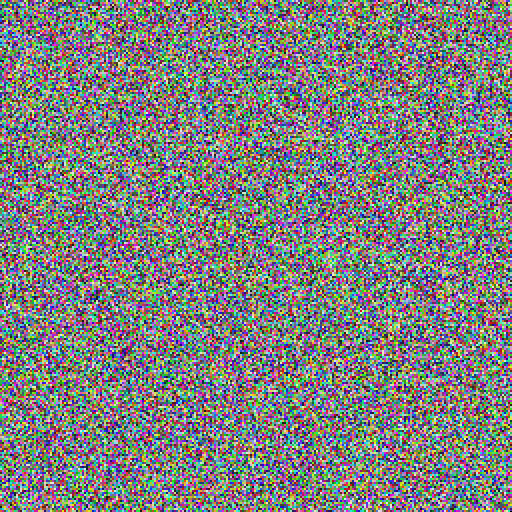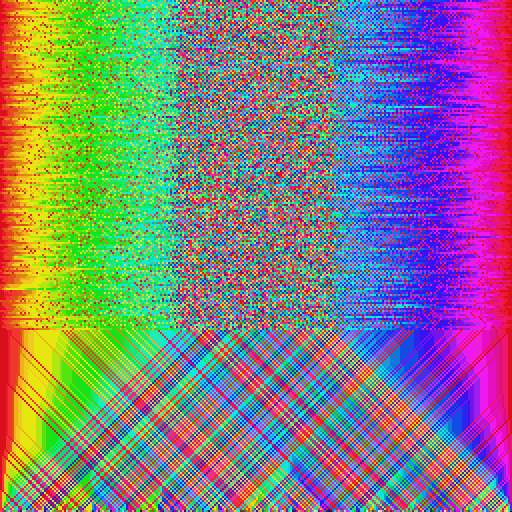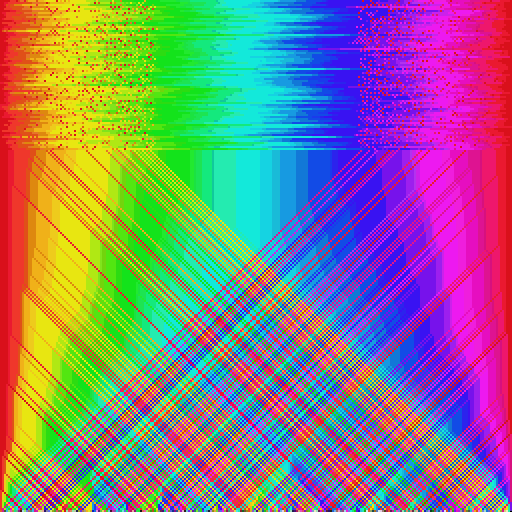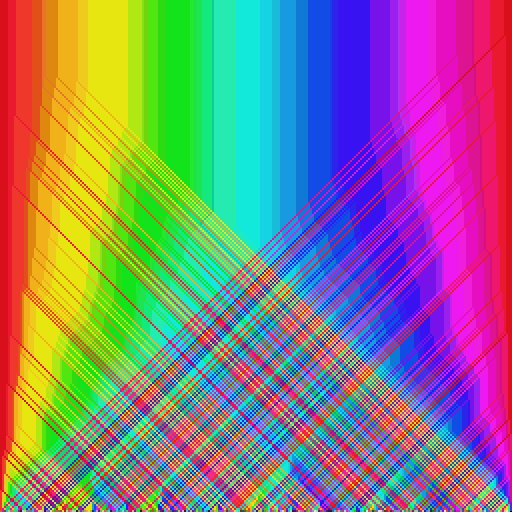
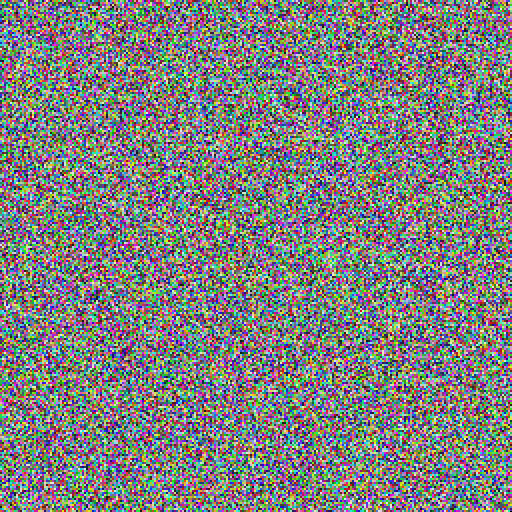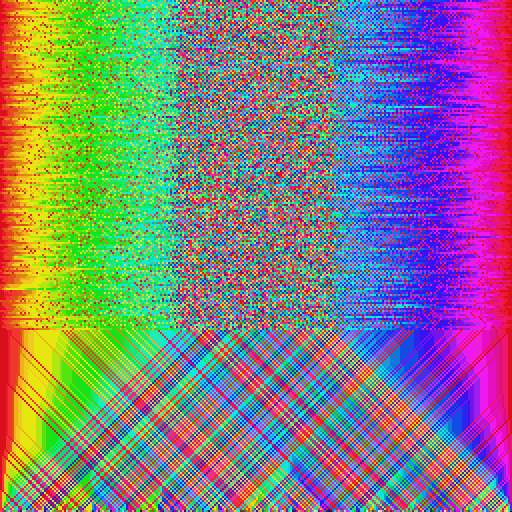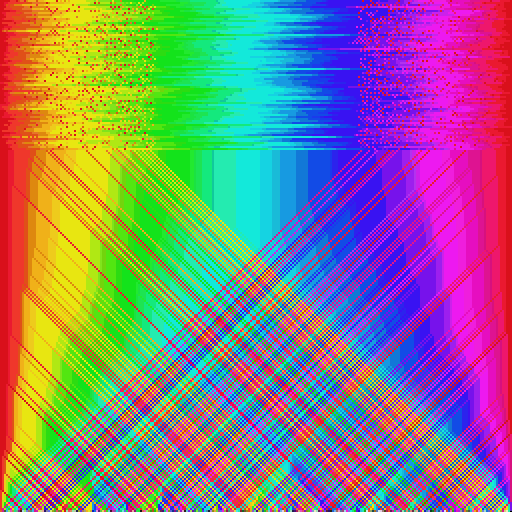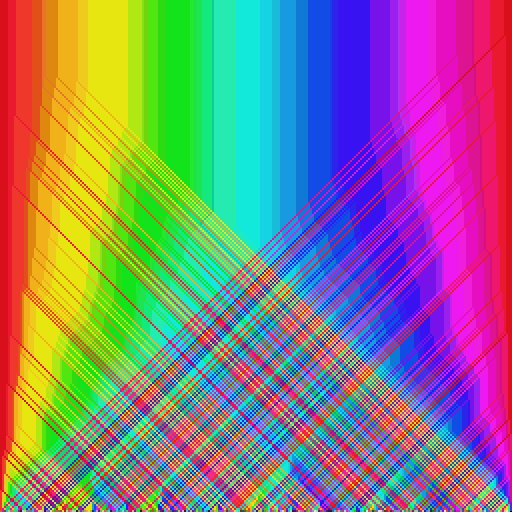
Введение
Если вы изучали теорию вычислительных машин в 80-х или 90-х, есть вероятность, что вы упорно пытались понять, что же некоторые разработчики находят восхитительного в алгоритмах сортировки. То, что поначалу кажется незначительной задачей, оказывается краеугольным камнем Computer Science.
Но что же такое «алгоритм сортировки»? Представьте, что у вас есть список чисел. Алгоритм сортировки — это программа, получающая этот список и изменяющая порядок чисел в нём. Понятие алгоритмов сортировки часто вводится при изучении вычислительной сложности — ещё одной обширной области знания, которую я подробно рассмотрю в будущих статьях. Существует бесконечное количество способов сортировки списка элементов, и каждая стратегия обеспечивает свой собственный уникальный компромисс между затратами и скоростью.
Бо́льшая часть сложности алгоритмов сортировки возникает из того, как мы определяем задачу, и как подходим к её решению. Чтобы решить, как менять порядок элементов, алгоритм должен сравнивать числа. С научной точки зрения каждое выполненное сравнение увеличивает сложность алгоритма. Сложность измеряется количеством выполняемых сравнений.
Однако не всё так просто: количество сравнений и замены элементов зависит от самого списка. Именно поэтому в теории вычислительных машин существуют более эффективные способы оценки производительности алгоритма. Каков наихудший сценарий работы алгоритма? Какое максимальное количество шагов он совершит для сортировки самого неотсортированного списка, с которым может работать? Такой способ рассмотрения задачи известен как анализ наихудших случаев. Мы можем задать тот же вопрос в наилучшем сценарии. Какое минимальное количество сравнений должен выполнить алгоритм для сортировки массива? Если упростить, то последняя задача часто относится к обозначению «О» большое, которое измеряет сложность как функцию количества сортируемых элементов
Но O(n log n) означает другое!
Если вы знакомы с обозначением «О» большое, то можете понять, что в предыдущем параграфе мы очень упростили объяснение.
Можно представить «О» большое как способ выражения "порядка величины" функции. То есть с
с  элементами на самом деле не означает, что будет
элементами на самом деле не означает, что будет  сравнения. Их может быть в 10, или даже в 100 раз больше. Для поверхностного понимания важно, что количество сравнений, необходимое для сортировки массива, растёт пропорционально
сравнения. Их может быть в 10, или даже в 100 раз больше. Для поверхностного понимания важно, что количество сравнений, необходимое для сортировки массива, растёт пропорционально  .
.
В будущих статьях я рассмотрю тему вычислительной сложности с чисто математической точки зрения.
Можно представить «О» большое как способ выражения "порядка величины" функции. То есть
В будущих статьях я рассмотрю тему вычислительной сложности с чисто математической точки зрения.
Ограничения видеопроцессора
Традиционные алгоритмы сортировки создаются на основании двух основных концепций:
- Сравнение: операция, сравнивающая два элемента списка и определяющая, какой из них больше;
- Замена: перемена мест двух элементов для приведения списка в состояние, более близкое к требуемому.
Список, который нужно отсортировать, часто задаётся в виде массива. Доступ к произвольным элементам массива чрезвычайно эффективен, и в нём без всяких ограничений можно менять местами любые два элемента.
Если мы хотим воспользоваться для сортировки шейдером, то нам для начала разобраться с неотъемлемыми ограничениями новой среды. Несмотря на то, что шейдеру можно передать список чисел, это будет не самый лучший способ использования его параллельности. Концептуально можно представить, что GPU выполняет одинаковый код шейдера одновременно для каждого пикселя. Обычно такого не происходит, потому что видеопроцессору скорее всего не хватит вычислительной мощности для распараллеливания вычислений для каждого пикселя. Некоторые части изображения будут обрабатываться параллельно, но мы не должны делать предположения о том, какие это именно части. По этому код шейдера должен выполняться при тех же ограничениях истинного параллелизма, даже если на самом деле он выполняется так не всегда.
Однако более серьёзное ограничение заключается в том, что код шейдера локализован. Если GPU выполняет часть кода для пикселя в координате
Сортировка в видеопроцессоре
Концепция представленного в данной статье подхода проста.
- Сортируемые данные передаются в виде текстуры;
- Если у нас есть массив
элементов, мы создаём текстуру размером
пикселей;
- Значение красного канала каждого пикселя содержит сортируемое число;
- Каждый проход рендеринга будет приближать массив к конечному состоянию.
Например, давайте представим, что у нас есть для сортировки список из четырёх чисел:

Как сказано выше, операция перемены мест при выполнении в шейдере гораздо более сложна, потому что она должна выполняться параллельно двумя независимыми пикселями. Простейший способ работы с таким ограничением является перемена местами соседних пар пикселей:
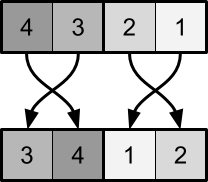
Важно добавить, что по сравнению с выполнением в ЦП, процесс выполняется почти в обратном порядке. Первый пиксель сэмплирует своё предыдущее значение
Поскольку эти вычисления выполняются независимо друг от друга, обе части кода должны «договориться» безо всякого общения, какое из значений опускать вниз. В этом и заключается сложность параллельной сортировки. Если мы не будем внимательны, оба пикселя пары замены возьмут одинаковое число, таким образом дублировав его.
Если мы повторим процесс замены, ничего не изменится. Каждая пара может отсортироваться за один шаг. Воспроизведение этого процесса не приведёт ни к каким изменениям. Чтобы справиться с этим, нужно изменить пары замены. Мы можем увидеть это на следующей схеме:
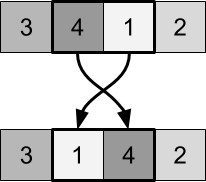
А что насчёт пикселей по краям?
Существует несколько решений, которые можно использовать для расширения этого решения для работы с первым и последним пикселями.
Первый подход — считать эти два пикселя частью одной пары замены. Такой подход сработает, но потребует создания дополнительных условий, что в коде шейдера неизбежно приведёт к снижению производительности.
Более простое решение заключается в простой обрезке текстуры. Два крайних пикселя будут выполнять замены сами с собой:
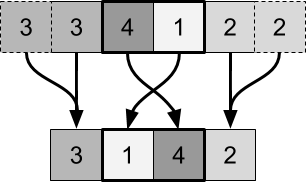
Первый подход — считать эти два пикселя частью одной пары замены. Такой подход сработает, но потребует создания дополнительных условий, что в коде шейдера неизбежно приведёт к снижению производительности.
Более простое решение заключается в простой обрезке текстуры. Два крайних пикселя будут выполнять замены сами с собой:

Мы можем попеременно использовать эти два шага, пока не будет отсортировано всё изображение:
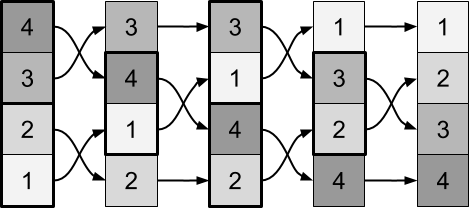
Такая техника существует уже довольно давно, и реализована во множестве стилей и вариаций. Часто её называют сортировкой чёт-нечет, потому что пары замены имеют нечётные/чётные и чётные/нечётные индексы. Этот рабочий механизм глубоко связан с сортировкой пузырьком, поэтому неудивительно, что алгоритм часто называют параллельной сортировкой пузырьком.
Сложность
При работе с видеопроцессором мы должны считать, что одинаковый код шейдера одновременно выполняется для каждого пикселя. В традиционном ЦП мы должны считать каждое сравнение/замену отдельной операцией. Проход шейдера будет считаться
Какой будет сложность в наихудшем случае? Мы видим, что каждый шаг перемещает пиксель к его конечной позиции. Максимальное перемещение пикселя равно
Если посмотреть на эту задачу с более традиционной перспективы, то всё становится сложнее. Каждый проход шейдера по крайней мере один раз анализирует каждый пиксель, то есть добавляет сложность
Часть 2. Реализация шейдера.
Шейдеры для симуляции
Шейдеры обычно используются для обработки передаваемых им текстур. Результаты их работы визуализируются на экране, а сами текстуры не изменяются. В этой статье мы хотим сделать нечто иное, потому что хотим, чтобы шейдер итеративно работал с одной текстурой. Мы подробно рассматривали, как это делается, в предыдущей серии постов How to Use Shaders for Simulations.
Идея заключается в том, чтобы создать две текстуры рендера — особые текстуры, которые можно изменять в шейдере. На схеме ниже показано, как работает это процесс.

Две текстуры рендера циклически меняются местами так, что проход шейдера использует предыдущую в качестве входных данных, а вторую — в качестве выходных.
В этой статье мы воспользуемся реализацией, представленной в посте How to Use Shaders for Simulations. Если вы ещё его не читали, то не волнуйтесь. Мы сосредоточимся только на самом алгоритме, вам достаточно знать следующее:
float4 frag(vertOutput i) : COLOR
{
// Координаты X, Y пикселя [0, _Pixels-1]
float2 xy = (int2)(i.uv * _Pixels);
float x = xy.x;
float y = xy.y;
// UV-координаты пикселя [0,1]
float2 uv = xy / _Pixels;
// UV-размер одного пикселя
float s = 1.0 / _Pixels;
...
}Во фрагментной функции шейдера будет содержаться код сортировки. Переменная
uv обозначает UV-координаты текущего отрисовываемого пикселя, а s представляет размер пикселя в UV-пространстве.Изменение порядка в паре замены
В предыдущей части мы ввели понятие пары замены. Пиксели группируются в пары, которые затем сортируются за один проход шейдера. Давайте представим два соседних пикселя, цвета которых
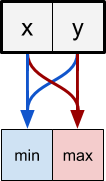
Чтобы сделать это, пиксель из левой части пары замены сэмплирует два пикселя выше и выбирает в качестве своего конечного цвета

Позиция пикселя определяет не только операции, которые нужно сделать, но и сэмплируемые пиксели. Min pixels должен сэмплировать пиксели в текущей позиции и справа от неё. Max pixels должен сэмплировать пиксель слева.
// Операция max
float3 C = tex2D(_MainTex, uv).rgb; // Текущий пиксель
float3 L = tex2D(_MainTex, uv + fixed2(-s, 0)).rgb; // Левый пиксель
result = max(L, C);
// Операция min
float3 C = tex2D(_MainTex, uv).rgb; // Текущий пиксель
float3 R = tex2D(_MainTex, uv + fixed2(+s, 0)).rgb; // Правый
result = max(C, R);Кроме того, пиксели min и max меняются местами после каждой операции. На схеме ниже показано, какие пиксели выполняют операцию min (синие), а какие — операцию max (красные):

Двумя определяющими факторами в выборе выполняемой операции являются номер итерации
_Iteration и индекс элемента x (или y, если мы сортируем не строки, а столбцы).Посмотрев на представленную выше схему, мы можем вывести последнее условие, позволяющее определить, какую операцию нужно выполнять — min или max:
// Макрос чёт/нечет
#define EVEN(x) (fmod((x),2)==0)
#define ODD(x) (fmod((x),2)!=0)
float3 C = tex2D(_MainTex, uv).rgb; // Центр
if ( ( EVEN(_Iteration) && EVEN(x) ) ||
( ODD (_Iteration) && ODD (x) )
)
{
// Операция max
float3 L = tex2D(_MainTex, uv + fixed2(-s, 0)).rgb; // Левый
result = max(L, C);
}
else
{
// Операция min
float3 R = tex2D(_MainTex, uv + fixed2(+s, 0)).rgb; // Правый
result = min(C, R);
}Это условие гарантирует, что во время чётных итераций (второй, четвёртой, …) пиксели в чётной позиции будут выполнять операцию max, а пиксели в нечётной позиции — операцию min. В нечётных итерациях (первой, третьей, …) происходит обратное.
Чтобы этот эффект работал, обеим текстурам рендера нужно задать Clamp, потому что код шейдера не имеет никаких граничных условий, мешающих получить доступ к пикселям за пределами текстуры.
Заключение
Другие анимации сортировки можно найти в этой галерее:
Анимации
[Прим. пер.: на странице автора в Patreon можно платно скачать Standard и Premium версии шейдера.]