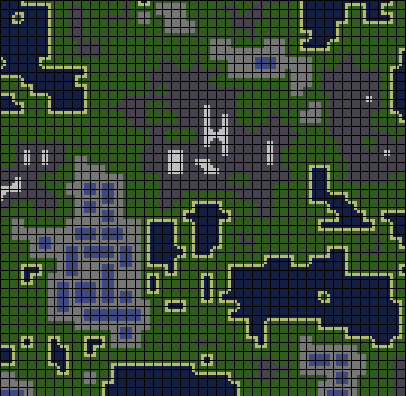
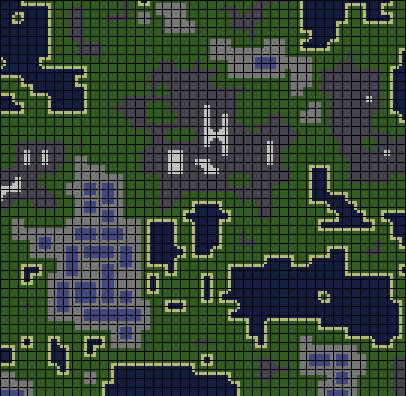
В этом посте я опишу два алгоритма для создания сложных процедурных миров из простых наборов цветных тайлов и на основе ограничений расположения этих тайлов. Я покажу, как при аккуратном дизайне этих наборов тайлов вы можете создавать интересный процедурно генерируемый контент, например, ландшафты с городами или подземелья со сложной внутренней структурой. В видео ниже показана система, создающая процедурный мир на основании правил, закодированных в 43 цветных тайлах.
На изображении ниже показан набор тайлов (тайлсет), на основании которого сгенерирован мир из видео. Мир снабжён примечаниями, которые помогут представить его в настоящей среде.
Мы можем определить тайлинг как конечную сетку, в которой каждый из тайлов находится в своей ячейке сетки. Правильный мир мы определим как мир, в котором цвета вдоль граней соседних тайлов должны быть одинаковыми.
У тайлинга есть только одно железное правило: цвета граней тайлов должны совпадать. Вся высокоуровневая структура развивается на основании этого правила.
Правильный тайлинг выглядит так:
Это тайлинг, который должен представлять карту с водой, побережьями, травой, городами со зданиями (синие прямоугольники), и горами со снежными вершинами. Чёрными линиями показаны границы между тайлами.
Я думаю, что это интересный способ описания и создания миров, потому что очень часто в алгоритмах процедурной генерации используется подход «сверху вниз». Например, в L-системах используется рекурсивное описание объекта, при котором высокоуровневые, крупные детали, определяются раньше, чем низкоуровневые. В таком подходе нет ничего плохого, но я думаю, что интересно создавать наборы тайлов, способные кодировать только простые низкоуровневые взаимоотношения (например, морская вода и трава должны быть разделены побережьем, у зданий должны быть только выпуклые углы под углами в 90 градусов) и наблюдать за возникновением высокоуровневых паттернов (например, квадратных зданий).
Тайлинг — это NP-полная задача удовлетворения ограничений
Для читателя, знакомого с задачами удовлетворения ограничений (ЗУО, constraint satisfaction problems, CSP), уже очевидно, что тайлинг конечного мира является ЗУО. В ЗУО у нас имеется множество переменных, множество значений, которые может принимать каждая переменная (называемое областью её определения) и множество ограничений. В нашем случае переменные — это координаты на карте, область определения каждой переменной — это тайлсет, а ограничения заключаются в том, что грани тайлов должны соответствовать граням соседей.
Интуитивно понятно, что задача правильного создания нетривиального тайлинга сложна, поскольку тайлсеты могут кодировать произвольные обширные зависимости. Когда мы рассматриваем тайлсет в целом, то с формальной точки зрения это является NP-полной задачей удовлетворения ограничений. Наивный алгоритм создания тайлингов заключается в исчерпывающем поиске пространства тайлингов и выполняется за экспоненциальное время. Существует надежда, что мы можем создавать интересные миры на основе тайлсетов, решаемых поиском, который можно ускорить эвристиками. Другой вариант — создавать тайлинги, которые приблизительно верны, но содержат небольшое количество неверных расположений. Я нашёл два алгоритма, которые хорошо работают с некоторыми интересными тайлсетами, и ниже опишу их.
Способ 1: жадное расположение с обратными переходами
Выбираем случайные места и помещаем туда подходящие тайлы. Если мы застрянем, удаляем некоторые из них и пробуем снова.
Инициализируем всю карту как НЕРЕШЁННУЮ
пока на карте остаются НЕРЕШЁННЫЕ тайлы
если на карте можно разместить любой подходящий тайл
t <- коллекция всех возможных расположений подходящих тайлов
l <- случайная выборка из t, взвешенная по вероятностям тайлов
располагаем l на карте
иначе
выбираем случайный НЕРЕШЁННЫЙ тайл и присваиваем всем его соседям состояние НЕРЕШЁННЫЙПервая попытка создания тайлинга из тайлсета заключалась в том, что вся сетка находилась в нерешённом состоянии, после чего я итеративно располагал случайный тайл в подходящем для него месте, или, если подходящих мест не было, присваивал небольшой области рядом с нерешённым тайлом состояние «нерешённая» и продолжал жадное расположение тайлов. «Жадное расположение» — это стратегия расположения тайла до тех пор, пока его грани соответствуют уже размещённым тайлам вне зависимости от того, будет ли такое расположение создавать частичный тайлинг, который невозможно завершить без замены уже поставленных тайлов. Когда возникает такая ситуация и мы больше не можем расположить тайлы, то мы должны удалить некоторые из ранее расположенных тайлов. Но мы не знаем, какие из них лучше всего убирать, потому что если бы мы могли решить задачу, то, вероятно, могли бы также в первую очередь решить задачу правильного расположения тайлов. Чтобы предоставить алгоритму ещё один шанс на нахождение подходящего тайла для заданной области, мы присваиваем всем тайлам вокруг нерешённой точки состояние «нерешённый» и продолжаем выполнять стратегию жадного расположения. Мы надеемся, что рано или поздно правильный тайлинг будет найден, но гарантий этого нет. Алгоритм будет выполняться, пока не найдётся правильный тайлинг, что может занять бесконечное время. Он не обладает способностью определять, что тайлсет нерешаем.
Нет никаких гарантий, что алгоритм завершит свою работу. Простой тайлсет с двумя тайлами, не имеющими общих цветов, заставит алгоритм выполнять бесконечный цикл. Ещё более простым случаем будет один тайл с разными цветами сверху и снизу. Разумно будет найти какой-то способ определения того, что тайлсеты не могут создавать правильные тайлинги. Мы можем сказать, что тайлсет определённо является верным, если он может замостить бесконечную плоскость. В некоторых случаях можно легко доказать, что тайлсет может или не может замостить бесконечную плоскость, но в общем случае эта задача является нерешаемой. Поэтому задача дизайнера заключается в том, чтобы создать тайлсет, способный создавать правильный тайлинг.
Этот алгоритм неспособен найти хороших решений для тайлсета подземелья из видео в начале поста. Он хорошо работает с более простыми тайлсетами. Нам бы хотелось научиться решать более сложные тайлсеты со множеством возможных типов переходов между тайлами и различными закодированными правилами (например, что дороги должны начинаться и заканчиваться рядом со зданиями).
Нам нужен алгоритм, способный заглядывать вперёд и создавать расположения тайлов, каким-то образом осознавая варианты при которых эти расположения открыты для будущих размещений тайлов. Это позволит нам эффективно решать сложные тайлсеты.
С точки зрения удовлетворения ограничениям
Этот алгоритм аналогичен поиску с обратным переходом. На каждом шаге мы пытаемся присвоить одну переменную. Если мы не можем, то отменяем присвоение переменной и всех переменных, которые присоединены к ней ограничениями. Это называется «обратным переходом» (backjumping) и отличается от возврата назад (backtracking), при котором мы отменяем присвоение одной переменной за раз, пока не сможем продолжать выполнять правильные присвоения. При возвратах назад мы в общем случае отменяем присвоение переменных в обратном порядке относительно их присвоения, однако при обратном переходе мы отменяем присвоение переменных согласно структуре рассматриваемой задачи. Логично, что если мы не можем поместить любой тайл в конкретную точку, то мы должны изменить расположение соседних тайлов, поскольку их расположение создало нерешаемую ситуацию. Возврат назад вместо этого может привести нас к отмене присвоения переменных, которые пространственно находятся далеко друг от друга, но были присвоены недавно.
В этом поиске не используются никакие методы обеспечения локальной целостности. То есть мы не предпринимаем попыток расположения тайлов, которые позже приведут к нерешаемой ситуации, даже через один шаг поиска в будущем. Возможно ускорение поиска благодаря отслеживанию влияния, которое расположение будет иметь на возможные расположения в нескольких тайлах от текущей точки. При этом можно надеяться, что это позволит поиску не тратить так много времени на отмену своей работы. Именно этим и занимается наш алгоритм.
Способ 2: расположение с наибольшими ограничениями и распространением локальной информации
Сохраняем распределение вероятностей для тайлов в каждой точке, внося нелокальные изменения в эти распределения при принятии решения о расположении. Никогда не выполняем возврата назад.
Далее я опишу алгоритм, который гарантированно завершается и создаёт более визуально приятные результаты для всех протестированных мной тайлов. Кроме того, он может создавать почти верные тайлинги для гораздо более сложных тайлсетов. Компромисс здесь заключается в том, что этот алгоритм не гарантирует, что выходной результат всегда будет верным тайлингом. В разделе «Оптимизации» описаны оптимизации, позволяющие выполнять это алгоритм быстрее даже при более крупных тайлсетах и картах.
Сложность создания верного тайлинга сильно зависит от количества переходов, необходимых для перехода между двумя типами тайлов. В простом тайлсете могут быть только песок, вода и трава. Если трава и вода не могут касаться друг друга, то между ними обязательно должен быть переход к песку. Это простой пример, который легко может решить представленный ранее алгоритм. В более сложном случае могут быть представлены множественные встроенные уровни типов тайлов. Например, у нас могут быть глубокая вода, вода, песок, трава, высокая равнина, гора и снежная вершина. Чтобы на карте могли появиться все эти типы тайлов, необходимо наличие семи переходов, если считать, что эти типы не могут касаться друг друга кроме как в указанном мной порядке. Дополнительная сложность может быть добавлена созданием тайлов, естественным образом создающих обширные зависимости между тайлами, например, дорог которые должны начинаться и заканчиваться рядом с определёнными типами тайлов.
Интуитивно понятно, алгоритм для этой задачи должен иметь возможность «заглядывать вперёд» и рассматривать хотя бы несколько переходов, которые могут стать последствиями выбранного расположения. Чтобы реализовать это, можно рассматривать тайловую карту как распределение вероятностей для тайлов в каждой точке. Когда алгоритм располагает тайл, он обновляет распределения вероятностей вокруг этого тайла в ответ на его расположение таким образом, что повышаются вероятности соседних тайлов, которые вероятно могут быть совместимы с текущим расположением.
Например, если на карте расположен тайл воды, то тайлы рядом с ним должны содержать воду. Тайлы рядом с ними тоже могут содержать воду, но существуют и другие вероятности, например, трава, если рядом с исходным тайлом воды помещено побережье. Чем дальше мы уходим от расположенного тайла, тем больше типов тайлов становится возможно. Чтобы воспользоваться этим наблюдением, мы можем считать количество способов, которыми мы можем дойти до расположения каждого тайла рядом с исходным тайлом. В некоторых случаях только единственная последовательность переходов может привести к переходу одного тайла к другому на заданном расстоянии. В других случаях может быть множество различных последовательностей переходов. После расположения тайла мы можем определить распределения вероятностей тайлов в соседних точках, посчитав количество способов, которыми мы можем совершить переход от тайла, который мы расположили, до соседних тайлов. Выполняемый этим алгоритмом «взгляд вперёд» — это отслеживание таких количеств переходов и обработка их как распределений вероятностей, из которых можно выбирать располагаемые новые тайлы.
На каждом шаге алгоритм исследует все нерешённые места расположения тайлов, каждое из которых имеет распределение вероятностей по тайлам, и выбирает одно место для «схождения» к тайлу. Он выбирает распределение из карты с минимальной энтропией. У мультиномиальных распределений с низкой энтропией вероятности обычно сконцентрированы в нескольких модах, поэтому схождение этих первых приводит к эффекту расположения тайлов, для которых уже есть некоторые из ограничений. Именно поэтому алгоритм располагает тайлы рядом с тайлами, которые мы решили сначала.
Это самый эффективный алгоритм, который мне удалось реализовать для этой задачи. Он имеет ещё одно преимущество: создаёт при выполнении красивые визуализации. Возможно, существует способ улучшить этот алгоритм, введя некую форму возврата назад. Если в получившемся готовом тайлинге существует неправильная точка, то отмена расположений соседних тайлов и ресэмплинг из получившихся распределений в их точках может позволить найти исправление этого готового тайлинга. Разумеется, если вы хотите продолжать поиск вплоть до нахождения верного тайлинга, то превысите пределы указанного гарантированного времени выполнения.
Оптимизации
Важнейшая операция этого способа — это обновление вероятностей вокруг расположенного тайла. Одним из подходов будет подсчёт возможных переходов «наружу» от расположенного тайла каждый раз при расположении тайла. Это будет очень медленно, поскольку для каждой точки карты, на которую распространятся новые вероятности, необходимо будет рассмотреть множество пар перехода. Очевидной оптимизацией будет выполнение распространения не на всю карту. Более интересная оптимизация заключается в кэшировании влияния, которое будет иметь каждое расположение тайлов на точки вокруг него, чтобы каждое расположение тайлов просто выполняло поиск для проверки того, какие типы изменений вносит расположение в соседние вероятности, с последующим применением этого изменения с помощью какой-то простой операции. Ниже я опишу мою реализацию этого способа оптимизации.
Представьте тайл, помещаемый на совершенно пустую карту. Это расположение обновит вероятности соседних тайлов. Мы можем рассматривать эти обновлённые распределения, как имевшие предыдущее распределение, заданное предыдущими расположениями тайлов. Если помещено несколько тайлов, то это предыдущее распределение будет совместным. Я аппроксимирую это апостериорную вероятность с учётом предыдущего совместного как произведение распределений для каждого расположения в прошлом.
Чтобы реализовать это, я представлю, что при расположении тайла на пустой карте он вносит значительные изменения в распределения соседних точек карты. Я назову эти обновления сферой тайла, то есть сферой влияния тайла, проецируемой вокруг него при помещении его на пустую карту. Когда два тайла располагаются друг рядом с другом, то их сферы взаимодействуют и создают конечные распределения, на которые влияют оба расположения. Учитывая то, что многие тайлы могут быть расположены рядом с заданным нерешённым местом, будет существовать большое количество взаимодействующих ограничений, делающее решение на основе подсчёта для определения вероятности появления разных тайлов в этой точке очень медленным процессом. Что, если вместо этого мы рассмотрим только простую модель взаимодействия между предварительно вычисленными сферами тайлов, которые уже были расположены на карте?
При расположении тайла я обновляю карту вероятностей для каждого элемента, умножая распределение сфера этого тайла на каждую точку карты на распределение, уже хранящееся в этой точке карты. Возможно, будет полезно рассмотреть пример того, что это может сделать с картой распределений. Допустим, у заданной точки карты в текущий момент есть распределение, которое с равной вероятностью может выбрать траву или воду, и мы помещаем рядом с этой точкой тайл воды. Сфера тайла воды будет иметь высокую вероятность воды рядом с тайлом воды и низкую вероятность тайла травы. Когда мы поэлементно перемножаем эти распределения, то вероятность воды в результате будет высокой, потому что это произведение двух больших вероятностей, но вероятность травы станет низкой, потому что это произведение высокой вероятности, хранящейся на карте, с низкой вероятностью, хранящейся в сфере.
Эта стратегия позволяет нам эффективно аппроксимировать влияние, которое должно иметь каждое расположение тайла на карту вероятностей.
С точки зрения удовлетворения ограничений
Для эффективного решения задач удовлетворения ограничений часто разумно отслеживать те присвоения других переменных, которые становятся невозможными при присвоении определённой переменной. Этот принцип называется введением условий локальной совместимости. Введение какого-нибудь вида локальной совместимости позволяет избежать присвоения переменной значения при присвоении соседней переменной несовместимого значения, когда возникает необходимость возврата назад. Такие преобразования относятся в литературе по ЗУО к области методов распространения ограничений. В нашем алгоритме мы распространяем информацию на небольшую область карты каждый раз, когда мы помещаем тайл. Распространяемая информация сообщает, какие тайлы могут и какие не могут возникнуть рядом. Например, если мы располагаем тайл горы, то знаем, что в двух тайлах от него не может быть тайла открытого моря, то есть вероятность тайла моря во всех точках карты в двух тайлах от расположенного тайла равна нулю. Эта информация записывается в сферы, о которых мы говорили выше. Сферы кодируют локальную совместимость, которую мы хотим наложить.
Снижая количество возможных присвоений соседних тайлов, мы значительно уменьшаем пространство поиска, которое должен обрабатывать алгоритм после каждого расположения. Мы знаем, что в этой небольшой окрестности все вероятности появления несовместимых с местом тайлов равны нулю. Это аналогично удалению этих значений из областей определения переменных в этих точках. То есть каждая пара соседних точек области вокруг расположенного тайла имеет в своей области определения некий тайл, совместимый с каким-то тайлом, всё ещё находящимся в области определения соседей. Когда две переменные соединены ограничением в задачу УО, а их области определения содержат только значения, удовлетворяющие ограничению, то говорят, что у них есть дуговая совместимость, то есть этот метод на самом деле является эффективной стратегией введения дуговой совместимости.
В ЗУО «наиболее ограниченная» переменная в заданном частичном присвоении — это та, у которой в области определения осталось меньше всего возможных значений. Принцип расположения тайла в точке минимальным распределением энтропии на карте аналогичен присвоению значения наиболее ограниченной переменной в ЗУО, что является стандартной эвристикой упорядочивания переменных при решении ЗУО при помощи поиска.
Манипуляции тайлингами изменением вероятностей выбора тайлов
Пока я рассказывал только о том, как создавать верные тайлинги, но кроме правильности, от тайлинга могут потребоваться и другие свойства. Например, нам может потребоваться определённое соотношение количества одного типа тайлов к другому, или же мы хотим гарантировать, что не все тайлы имеют одинаковый тип, даже если такой тайлинг является верным. Для решения этой задачи оба описываемых мной алгоритма получают в качестве входных данных базовую вероятность, связанную с каждым тайлом. Чем выше эта вероятность, тем вероятнее этот тайл будет присутствовать в готовом тайлинге. Оба алгоритма делают случайный выбор из коллекций тайлов, и я просто добавлю веса этому случайному выбору согласно базовым вероятностям тайлов.
Ниже показан пример использования этого принципа. Изменяя вероятность появления тайла сплошной воды, я могу регулировать размер и частоту появления на карте водоёмов.
Создаём собственные тайлсеты
Вкратце:
- клонируйте мой репозиторий на github
- установите Processing
- в папке data/ репозитория измените tiles.png
- используйте processing для открытия wangTiles.pde и нажмите на кнопку play
С помощью выложенного на github кода (можете изменять его, но делайте это на собственный страх и риск — бОльшую его часть я написал в старшей школе) вы можете создавать собственные тайлсеты, пользуясь редактором изображений, и наблюдать, как решатель тайлинга создаёт с их помощью миры. Просто клонируйте репозиторий и отредактируйте изображение dungeon.png, а затем воспользуйтесь Processing для запуска wangTiles.pde и просмотра анимации генерируемой карты. Ниже я опишу «язык», который требуется этому решателю тайлинга.
Спецификация тайлсетов
Тайлы расставлены сеткой из ячеек 4x4. Каждая ячейка в верхней левой области 3x3 содержит цветной тайл, а в оставшихся 7 пикселях содержатся метаданные тайла. Пиксель под центром тайла можно окрасить красным цветом, чтобы закомментировать тайл и исключить его из тайлсета. Решатели никогда не будут помещать его на карту. Верхний пиксель в правой части тайла можно закрасить чёрным, чтобы добавить в тайлсет все четыре поворота тайла. Это удобная функция, если вы хотите добавить что-то вроде угла, который существует в четырёх ориентациях. Наконец, самой важной частью разметки является пиксель в нижней левой части тайла. Он управляет базовой вероятностью появления тайла на карте. Чем темнее пиксель, тем больше вероятность появления тайла.
Близкие по теме работы
Многие люди исследовали Плитки Вана, которые являются тайлсетами с цветными гранями и должны соответствовать гранями с тайлами, рядом с которыми их помещают, точно так же, как и рассматриваемые нами тайлы.
Решатель «Most Constrained Placement with Fuzzy Arc Consistency» похож на проект Wave Function Collapse пользователя Twitter @ExUtumno. Этот алгоритм хранит карту «частично наблюдаемых» присвоений и для создания конечного изображения берёт из них выборки, что похоже на сохраняемые мной распределения для тайлов. Эти подходы в некоторых аспектах отличаются. Для каждой точки карты этот алгоритм сохраняет двоичные потенциалы, а не мультиномиальные распределения. Кроме того, он не использует кэшируемые «сферы» количеств переходов, необходимых для ускорения расчётов, о которых я рассказывал в разделе «Оптимизация».
Выводы и благодарности
Применение локальных правил для создания высокоуровневой структуры, например, введение правила «дороги не имеют тупиков» приводит к реализации такой системы, в которой дороги должны вести из какой-то точки, не являющейся дорогой, в другую. Это интересный взгляд на задачу процедурной генерации. Таким образом можно закодировать на удивление широкий диапазон интересных правил. Качество получающихся тайлингов очень сильно зависит от решателя, поэтому плодотворным направлением дальнейшей работы будет усовершенствование алгоритмов создания тайлинга. Пока для решения этой задачи я не изучал генетические алгоритмы, имитацию отжига или общие алгоритмы удовлетворения ограничениям. В любой из этих областей возможно создать решатель тайлсетов, способный справляться с широким диапазоном тайлсетов с минимальной настройкой параметров.
Я хотел бы поблагодарить Кэннона Льюиса и Ронни Макларена за полезные обсуждения в процессе работы над этим проектом. Ронни пришёл ко множеству любопытных идей о возможности кодирования в тайлах интересного поведения. Алгоритм схождения волн возник в результате общения с Кэнноном, а его советы стали важным этапом в создании описанного в статье эффективного алгоритма аппроксимации.