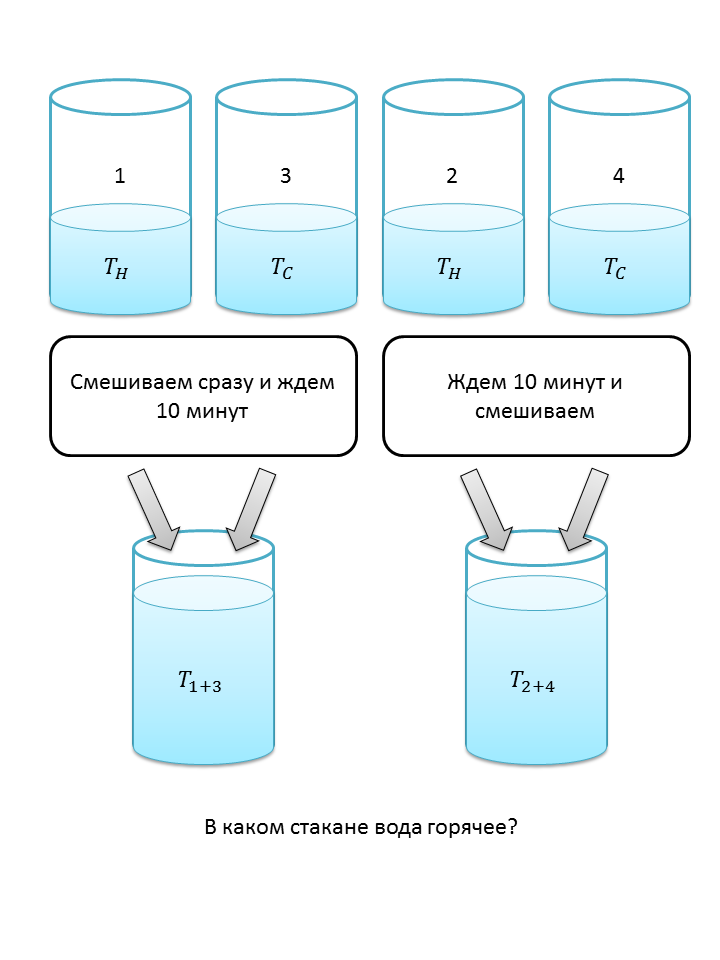
В комментариях к моему посту, одним из пользователей был задан интересный вопрос. Суть его такова: Имеем 4 стакана, с одинаковым объемом воды. 2 из них с горячей, 2 — с холодной. Смешиваем стаканы с горячей и холодной водой. Ждем 10 мин и смешиваем оставшиеся. Вопрос: в какой смеси вода будет горячее?

Нагрев и остывание подчиняются закону Ньютона-Рихмана, решение уравнений которого имеет вид:

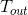 — температура окружающей среды;
— температура окружающей среды;
 — начальная температура;
— начальная температура;
 — время;
— время;
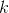 — коэффициент, описанный ниже;
— коэффициент, описанный ниже;
Давайте детально исследуем эту формулу:
Теперь несколько слов о коэффициенте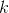 :
:

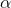 — коэффициент теплоотдачи, зависящий от многих факторов, получаемый экспериментально.
— коэффициент теплоотдачи, зависящий от многих факторов, получаемый экспериментально.
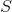 — площадь границы раздела;
— площадь границы раздела;
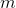 — масса;
— масса;
 — удельная теплоемкость тела;
— удельная теплоемкость тела;
Если с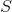 (площадь соприкосновения воды и стенок сосуда), удельной теплоемкостью
(площадь соприкосновения воды и стенок сосуда), удельной теплоемкостью  и массой
и массой 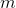 все понятно, то с коэффициентом теплоотдачи
все понятно, то с коэффициентом теплоотдачи 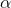 все не так очевидно. Он показывает, сколько джоулей за секунду уйдет через метр квадратный границы раздела, при разности температур в 1 Кельвин. К счастью, в нашем случае, не важно знание абсолютного значения этого коэффициента.
все не так очевидно. Он показывает, сколько джоулей за секунду уйдет через метр квадратный границы раздела, при разности температур в 1 Кельвин. К счастью, в нашем случае, не важно знание абсолютного значения этого коэффициента.
Какой станет итоговая температура воды после смешивания? Как бы банально это не звучало, но для нашего случая (смешиваем равное количество воды):
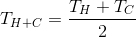
 — температура горячей (Hot) воды;
— температура горячей (Hot) воды;
 — температура холодной (Cold) воды;
— температура холодной (Cold) воды;
 — температура смеси;
— температура смеси;
Температура этих стаканов изменяется по экспоненциальному закону и через время станет:
станет:
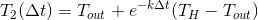

Далее смешиваем и получаем:


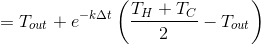
Смешиваем:

И через получаем:
получаем:
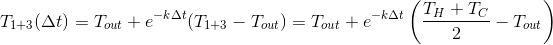
Казалось бы разницы нет, но…
Наш цилиндрический стакан с точки зрения потерь тепла, можно разбить на три зоны: дно (bottom), верхняя часть (top) и боковые стенки (sidewall). Поэтому и коэффициент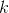 можно записать как сумму:
можно записать как сумму:
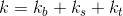 , где
, где
 ,
, 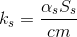 ,
, 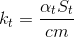
Если стакан рассматривать как цилиндр с радиусом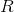 и высотой
и высотой  , то:
, то:
 , а
, а

Можем записать:

Так вот, для случая 1 и 3, при смешивании, масса и высота столба воды удваиваются:

А вот к случаю 2 и 4 это не имеет никакого отношения, так как остывают (нагреваются) они по-одиночке, и после смешивания, дальнейшее изменение температуры нас абсолютно не волнует.
Если рассматривать
 и
и

можно сделать вывод что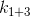 всегда будет меньше чем
всегда будет меньше чем 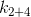 , а поэтому, если вспомнить что коэффициент определяет скорость изменения температуры, она, в случае 1 и 3 будет меньше.
, а поэтому, если вспомнить что коэффициент определяет скорость изменения температуры, она, в случае 1 и 3 будет меньше.
Подвох состоит в значении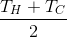 относительно температуры окружающей среды. Если это значение будет выше, то остывание смеси 1+3 будет медленее чем 2+4 и, как итог, температура первой — выше. Однако, если подстроить эксперимент таким образом, что среднее температур будет ниже окружающей — «горячее» будет смесь 2+4, так как она нагревается быстрее.
относительно температуры окружающей среды. Если это значение будет выше, то остывание смеси 1+3 будет медленее чем 2+4 и, как итог, температура первой — выше. Однако, если подстроить эксперимент таким образом, что среднее температур будет ниже окружающей — «горячее» будет смесь 2+4, так как она нагревается быстрее.
На самом деле, данная статья очень наглядный пример того, что к практике без теории подходить нельзя. И этот абзац содержит выводы куда важнее приведенных выше. Не знание того факта, что результат зависит, помимо прочего, и от температуры окружающей среды, приведет к неправильной интерпретации последних. Вы только представьте, два друга ставят эксперимент, холодная вода 5 градусов, горячая 60. Но у одного из них дома 25, а у другого 40. Результаты будут противоречивыми. А если у них еще и стаканы разные или действия не синхронны… Но гораздо хуже, ложно утверждать о единственно верном исходе эксперимента, в случае, если результаты одинаковы (ввиду того что горячая вода чаще всего «горячее» чем холодная «холоднее» относительно комнатной температуры). Также, всегда следует хотя бы приблизительно оценить выходные величины. Если, к примеру, разница в температурах, количественно составит 0.5 градуса, то глупо мерить ее комнатным термометром, с погрешностью в 2 градуса. Стоит упомянуть о том, что закон Ньютона-Рихмана справедлив лишь в том случае, если в воде тепло распространяется гораздо легче, чем через стенки стакана. Вдобавок коэффициент теплопроводности, как и удельная теплоемкость, может зависеть от температуры. Ну и выводы наши для цилиндрического стакана, и другая геометрия внесет свои коррективы.
Нагрев и остывание
Нагрев и остывание подчиняются закону Ньютона-Рихмана, решение уравнений которого имеет вид:

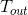 — температура окружающей среды;
— температура окружающей среды; — начальная температура;
— начальная температура; — время;
— время;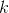 — коэффициент, описанный ниже;
— коэффициент, описанный ниже;Давайте детально исследуем эту формулу:
- в момент времени
 , температура равна начальной
, температура равна начальной  .Подробнее
.Подробнее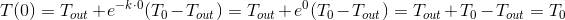
- с течением времени, она стремится к окружающей (в не зависимости, была начальная выше или ниже неё) по экспоненциальному закону, со скоростью, пропорциональной коэффициенту
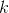 .ПобробнееТак как
.ПобробнееТак как , то
, то 
Теперь несколько слов о коэффициенте
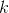 :
:
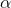 — коэффициент теплоотдачи, зависящий от многих факторов, получаемый экспериментально.
— коэффициент теплоотдачи, зависящий от многих факторов, получаемый экспериментально.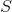 — площадь границы раздела;
— площадь границы раздела;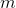 — масса;
— масса; — удельная теплоемкость тела;
— удельная теплоемкость тела;Если с
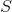 (площадь соприкосновения воды и стенок сосуда), удельной теплоемкостью
(площадь соприкосновения воды и стенок сосуда), удельной теплоемкостью  и массой
и массой 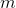 все понятно, то с коэффициентом теплоотдачи
все понятно, то с коэффициентом теплоотдачи 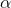 все не так очевидно. Он показывает, сколько джоулей за секунду уйдет через метр квадратный границы раздела, при разности температур в 1 Кельвин. К счастью, в нашем случае, не важно знание абсолютного значения этого коэффициента.
все не так очевидно. Он показывает, сколько джоулей за секунду уйдет через метр квадратный границы раздела, при разности температур в 1 Кельвин. К счастью, в нашем случае, не важно знание абсолютного значения этого коэффициента.Смешивание
Какой станет итоговая температура воды после смешивания? Как бы банально это не звучало, но для нашего случая (смешиваем равное количество воды):
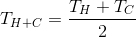
 — температура горячей (Hot) воды;
— температура горячей (Hot) воды; — температура холодной (Cold) воды;
— температура холодной (Cold) воды; — температура смеси;
— температура смеси;Доказательство
Количество выделенной или поглощенной энергии системы, c изменением ее температуры, связаны простым отношением:
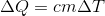
Горячая вода, охлаждаясь до отдаст такое же количество энергии, сколько заберет холодная, нагреваясь до той же температуры. Поэтому можем записать:
отдаст такое же количество энергии, сколько заберет холодная, нагреваясь до той же температуры. Поэтому можем записать:
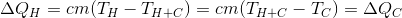


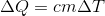
Горячая вода, охлаждаясь до
 отдаст такое же количество энергии, сколько заберет холодная, нагреваясь до той же температуры. Поэтому можем записать:
отдаст такое же количество энергии, сколько заберет холодная, нагреваясь до той же температуры. Поэтому можем записать: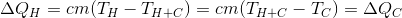


Стаканы 2 и 4
Температура этих стаканов изменяется по экспоненциальному закону и через время
 станет:
станет: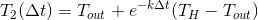

Далее смешиваем и получаем:


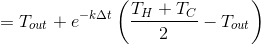
Стаканы 1 и 3
Смешиваем:

И через
 получаем:
получаем: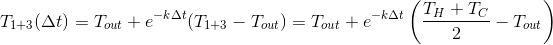
Казалось бы разницы нет, но…
Подвох или еще раз о коэффициенте k
Наш цилиндрический стакан с точки зрения потерь тепла, можно разбить на три зоны: дно (bottom), верхняя часть (top) и боковые стенки (sidewall). Поэтому и коэффициент
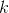 можно записать как сумму:
можно записать как сумму: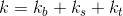
 ,
, 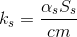 ,
, 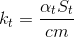
Если стакан рассматривать как цилиндр с радиусом
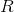 и высотой
и высотой  , то:
, то:

Можем записать:

Так вот, для случая 1 и 3, при смешивании, масса и высота столба воды удваиваются:

А вот к случаю 2 и 4 это не имеет никакого отношения, так как остывают (нагреваются) они по-одиночке, и после смешивания, дальнейшее изменение температуры нас абсолютно не волнует.
Выводы и еще один подвох
Если рассматривать


можно сделать вывод что
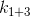 всегда будет меньше чем
всегда будет меньше чем 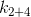 , а поэтому, если вспомнить что коэффициент определяет скорость изменения температуры, она, в случае 1 и 3 будет меньше.
, а поэтому, если вспомнить что коэффициент определяет скорость изменения температуры, она, в случае 1 и 3 будет меньше.Подвох состоит в значении
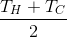 относительно температуры окружающей среды. Если это значение будет выше, то остывание смеси 1+3 будет медленее чем 2+4 и, как итог, температура первой — выше. Однако, если подстроить эксперимент таким образом, что среднее температур будет ниже окружающей — «горячее» будет смесь 2+4, так как она нагревается быстрее.
относительно температуры окружающей среды. Если это значение будет выше, то остывание смеси 1+3 будет медленее чем 2+4 и, как итог, температура первой — выше. Однако, если подстроить эксперимент таким образом, что среднее температур будет ниже окружающей — «горячее» будет смесь 2+4, так как она нагревается быстрее.Интересненькое
Если внимательно рассмотреть коэфициенты, можно сделать еще один интересный вывод.
Если подставить это значение в формулу итоговой температуры для 1+3, получим:

Напомним что

Если обозначить:
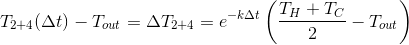
, и
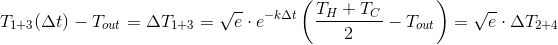
Таким образом, для произвольного цилиндрического стакана и ,
, 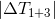 будет лежать между
будет лежать между 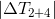 и
и  :
:

- Если цилиндр выбрать таким образом, что отношение
 будет достаточно большим (тонкий, но длинный), так чтобы
будет достаточно большим (тонкий, но длинный), так чтобы 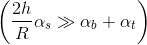 , то
, то  и их итоговые температуры будут практически одинаковы.
и их итоговые температуры будут практически одинаковы. - Напротив, если отношение
 сделать достаточно малым (широкий но короткий) так, чтобы
сделать достаточно малым (широкий но короткий) так, чтобы  , то
, то  .
.
Подробнее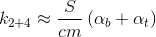

Если подставить это значение в формулу итоговой температуры для 1+3, получим:

Напомним что

Если обозначить:
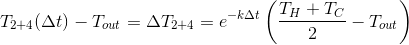
, и
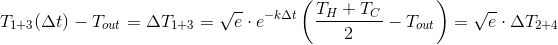
Таким образом, для произвольного цилиндрического стакана и
 ,
, 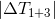 будет лежать между
будет лежать между 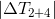 и
и  :
:
А на самом деле..?
На самом деле, данная статья очень наглядный пример того, что к практике без теории подходить нельзя. И этот абзац содержит выводы куда важнее приведенных выше. Не знание того факта, что результат зависит, помимо прочего, и от температуры окружающей среды, приведет к неправильной интерпретации последних. Вы только представьте, два друга ставят эксперимент, холодная вода 5 градусов, горячая 60. Но у одного из них дома 25, а у другого 40. Результаты будут противоречивыми. А если у них еще и стаканы разные или действия не синхронны… Но гораздо хуже, ложно утверждать о единственно верном исходе эксперимента, в случае, если результаты одинаковы (ввиду того что горячая вода чаще всего «горячее» чем холодная «холоднее» относительно комнатной температуры). Также, всегда следует хотя бы приблизительно оценить выходные величины. Если, к примеру, разница в температурах, количественно составит 0.5 градуса, то глупо мерить ее комнатным термометром, с погрешностью в 2 градуса. Стоит упомянуть о том, что закон Ньютона-Рихмана справедлив лишь в том случае, если в воде тепло распространяется гораздо легче, чем через стенки стакана. Вдобавок коэффициент теплопроводности, как и удельная теплоемкость, может зависеть от температуры. Ну и выводы наши для цилиндрического стакана, и другая геометрия внесет свои коррективы.