Шутки в сторону, тема серьёзная, пожароопасная. Поехали. Это третья статья из цикла, в ней рассмотрены модели оценки предельного тока печатной дорожки, который в некоторых ситуациях является определяющим параметром при выборе толщины проводящих слоёв печатной платы.
В предыдущей статье говорилось о том, выбор толщины медных слоёв печатной платы определяется, прежде всего, требуемыми минимальным зазором и минимальной шириной проводника, а также максимальным током, протекающим по проводнику. Эти параметры могут противоречить друг другу: чем тоньше проводящий слой, тем меньший топологический рисунок может быть получен, но тем меньший предельный ток выдержит печатная дорожка (при прочих равных условиях – ширина проводника, частота тока, теплоотвод и др.). Тепловая энергия Q выделяющаяся на омическом сопротивлении R печатной дорожки (джоулево тепло Q=I2Rt, где I – сила тока, t — время), вызывает повышение её температуры относительно окружающей среды, приводя к перегреву самого проводника и связанных с ним компонентов или, в крайнем случае, к его перегоранию при предельном токе (англ. fusing current). Соотношение между током через печатную дорожку и приростом температуры зависит от многих параметров и в общем виде трудно представимо, однако существуют формулы, позволяющие сделать предварительные оценки.
Одна из первых попыток принадлежит У.Г.Прису (англ. W.H.Preece). Свою эмпирическую зависимость он получил в лабораторном эксперименте, в котором он постепенно увеличивал ток через проводник до момента его накала докрасна. Формула Приса связывает ток накала c диаметром проводника d для различных материалов:

где K – табличная константа, примерно равная 80 для меди. Используя соотношение площади круга, можно переписать эту формулу для случая медного проводника с площадью сечения S:
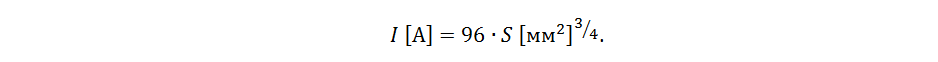
В эксперименте Приса проводник был подвешен в воздухе, в отличие от проводника на печатной плате, условия теплоотвода для которого совсем другие. Более близкими являются условия теплоотвода для случаев одиночного соединительного проводника, а также для некоторых случаев микропроволочной разварки (когда для её защиты не используется компаундирование), где эта формула может давать хорошую оценку для предельного тока.
Допустимым приростом температуры печатной дорожки обычно считается 10-30 ˚С. Это значение может быть и больше в зависимости от параметров проекта, однако во всём диапазоне рабочих температур изделия температура дорожки должна быть меньше температуры стеклования материала печатной платы (англ. glass transition temperature, Tg) и тем более температуры накала меди. Поэтому полезна зависимость прироста температуры ∆T от тока I печатной дорожки шириной w и толщиной фольги h, приведённая Д.Бруксом в [1]:
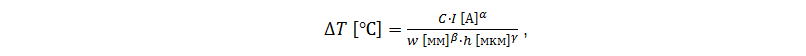
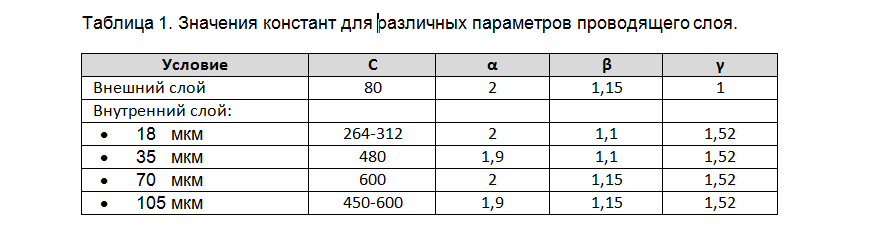
где C, α, β, γ – константы, значения которых для внешних и внутренних слоёв приведены в таблице 1. Стоит учитывать, что на внешних слоях толщина фольги обычно больше на 20-40 мкм относительно базового значения в связи с дополнительным напылением при создании переходных отверстий. Также влияние финишного покрытия на платах без маски может быть значительным. Это используют в силовых приборах, когда на вскрытую от маски печатную дорожку паяют дополнительный припой.
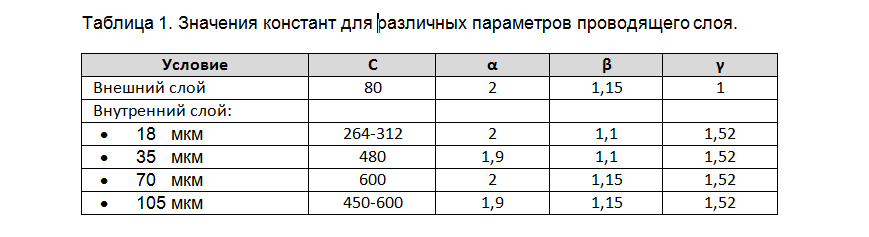
Ещё одной известной формулой расчёта предельной токонесущей способности проводника является формула Ондердонка (англ. I.M.Onderdonk), которая содержит такой важный параметр, как время. Она связывает время t пропускания тока I через медный проводник сечением S и прирост температуры ∆T относительно начальной температуры T0:
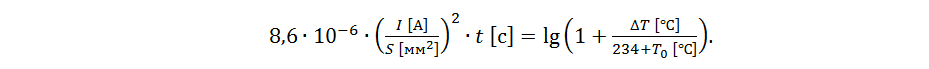
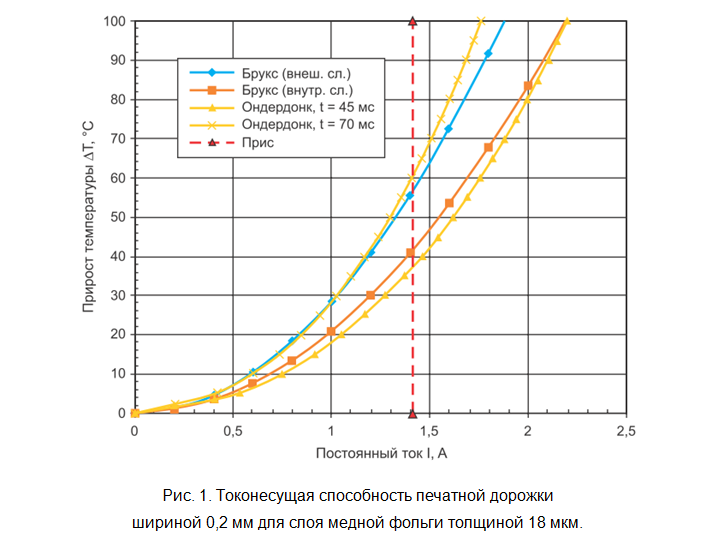
Так как при выводе формулы [2] исключается всякий теплоотвод, то для случая печатной дорожки эта формула применима для короткого импульса тока длительностью до 1-2 секунд. С увеличением времени и влияния теплоотвода точность оценки падает, в разы занижая предельный ток. Графики зависимостей по всем трём приведённым формулам для различных параметров печатной дорожки приведены на рисунках 1 и 2.


Всегда важно учитывать условия эксперимента или аналитические допущения при выводе, чтобы понимать границы применимости той или иной формулы. Ни одна из приведённых формул не даст точное и оптимальное соотношение между предельным током и требуемым сечением проводника для реальных приложений. Это же касается и простых калькуляторов, которые можно найти в сети Интернет (например), потому что они основаны на этих или аналогичных формулах. Влияние соседних проводников и компонентов как источников и приемников тепла, излучения, активного или пассивного охлаждения может быть учтено только при термоэлектрическом моделировании в специализированных САПР (таких как Cadence, ANSYS и других). Однако даже в этом случае результаты моделирования и эксперимента могут значительно отличаться. Дело в том, что печатная дорожка имеет не прямоугольное сечение, а близкое к трапециевидному (рис. 3), а её ширина и значение проводимости медной фольги могут не только отличаются от расчётных по модели, но и имеют некоторый разброс от образца к образцу, партии к партии, изготовителю к изготовителю и т.д. Влияние отклонений ширины усиливается с её уменьшением. Тем не менее, расчётные результаты по формулам и рекомендации стандартов чаще всего будут представлять наихудший случай, обеспечивая тем самым запас прочности системы. Если разработчику требуется оптимизировать соотношение между предельным током и требуемым сечением печатной дорожки, то к этой цели необходимо идти итеративным путём моделирования и эксперимента.

Увеличение сечения печатной дорожки пропорционально снижает её омическое сопротивление на единицу длины, что уменьшает тепловые потери при протекании постоянного тока. Ситуация с переменным током не так проста по причине существования скин-эффекта (англ. skin effect), который приводит к тому, что плотность переменного тока неравномерно распределена по сечению проводника, экспоненциально убывая до нуля от поверхности проводника к центру. Для удобства расчётов применяется понятие эффективного сечения проводника с глубиной, определяемой соотношением:
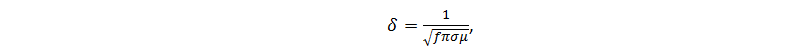
где f – частота тока, σ – проводимость металла, μ – магнитная проницаемость. На глубине равной δ плотность тока становится меньше в e раз относительно плотности тока на поверхности JS. Математически можно показать верность следующего приближённого равенства для плотности тока J(x,y) в проводнике:

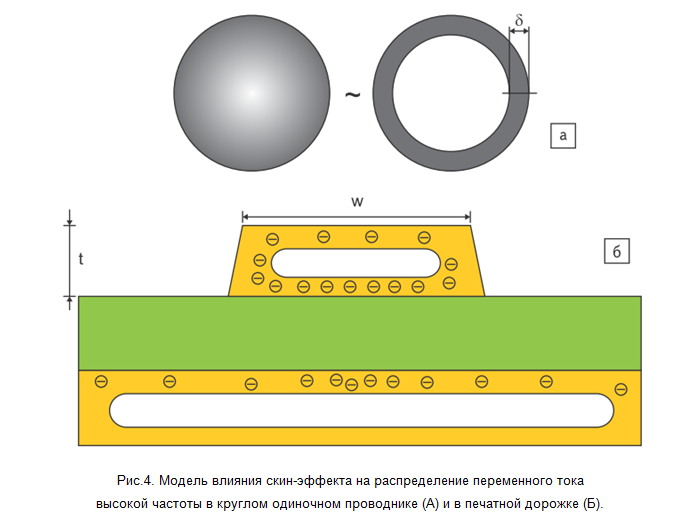
То есть для приближённых вычислений можно принять, что ток течёт только в граничном слое проводника периметра l глубиной δ, причём с равномерным распределением (рис. 4).
В рамках этой упрощённой модели, если глубина поверхностного слоя меньше половины толщины печатной дорожки, то импеданс печатной дорожки на данной частоте будет определяться именно этим эффективным сечением, приводя к увеличению омического сопротивления и незначительному снижению индуктивности. На рис. 5 представлена зависимость глубины поверхностного слоя от частоты тока с учётом разброса проводимости осаждённой меди. Из него видно, что для слоёв меди толщиной 18 мкм граничная частота (выше которой скин-эффект играет роль) находится в районе 50-70 МГц, а для слоёв толщиной 35 мкм – в районе 15-20 МГц. Отметим, что на частотах свыше 100 МГц глубина скин-эффекта меняется незначительно, это позволяет пренебрегать его зависимостью от частоты при расчётах для высокочастотных сигналов.

При проектировании печатных плат с постоянно действующими токами величиной в несколько ампер необходимо выполнять тепловые расчёты как для электрических компонентов, так и для проводников. Представленные модели и аналитические соотношения позволяют выполнить оценку предельного тока печатных дорожек и на её основании выбрать необходимую толщину медных слоёв и топологию проводников. Для получения точного решения необходимо использовать специализированные САПР, при этом желательно задавать геометрию с учётом технологических погрешностей изготовления и данные по проводимости меди, полученные от производителя печатных плат. Очень рекомендую ознакомиться со статьями Д.Брукса, посвящёнными подробному анализу методов оценки температуры печатных проводников, где представлены наглядные результаты моделирования температурных полей.
[1] Brooks D. G., Adam J. «Trace Currents and Temperatures Revisited», UltraCAD, 2015.
[2] Adam J., Brooks D. G. «In Search For Preece and Onderdonk», UltraCAD, 2015.
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №1. Публикация на «Geektimes» согласована с редакцией журнала.
В предыдущей статье говорилось о том, выбор толщины медных слоёв печатной платы определяется, прежде всего, требуемыми минимальным зазором и минимальной шириной проводника, а также максимальным током, протекающим по проводнику. Эти параметры могут противоречить друг другу: чем тоньше проводящий слой, тем меньший топологический рисунок может быть получен, но тем меньший предельный ток выдержит печатная дорожка (при прочих равных условиях – ширина проводника, частота тока, теплоотвод и др.). Тепловая энергия Q выделяющаяся на омическом сопротивлении R печатной дорожки (джоулево тепло Q=I2Rt, где I – сила тока, t — время), вызывает повышение её температуры относительно окружающей среды, приводя к перегреву самого проводника и связанных с ним компонентов или, в крайнем случае, к его перегоранию при предельном токе (англ. fusing current). Соотношение между током через печатную дорожку и приростом температуры зависит от многих параметров и в общем виде трудно представимо, однако существуют формулы, позволяющие сделать предварительные оценки.
Прис, Ондердонк и Брукс
Одна из первых попыток принадлежит У.Г.Прису (англ. W.H.Preece). Свою эмпирическую зависимость он получил в лабораторном эксперименте, в котором он постепенно увеличивал ток через проводник до момента его накала докрасна. Формула Приса связывает ток накала c диаметром проводника d для различных материалов:
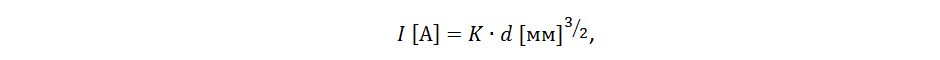
где K – табличная константа, примерно равная 80 для меди. Используя соотношение площади круга, можно переписать эту формулу для случая медного проводника с площадью сечения S:
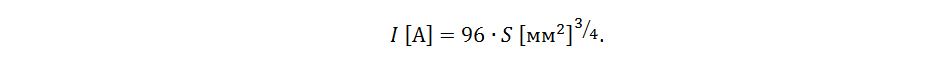
В эксперименте Приса проводник был подвешен в воздухе, в отличие от проводника на печатной плате, условия теплоотвода для которого совсем другие. Более близкими являются условия теплоотвода для случаев одиночного соединительного проводника, а также для некоторых случаев микропроволочной разварки (когда для её защиты не используется компаундирование), где эта формула может давать хорошую оценку для предельного тока.
Допустимым приростом температуры печатной дорожки обычно считается 10-30 ˚С. Это значение может быть и больше в зависимости от параметров проекта, однако во всём диапазоне рабочих температур изделия температура дорожки должна быть меньше температуры стеклования материала печатной платы (англ. glass transition temperature, Tg) и тем более температуры накала меди. Поэтому полезна зависимость прироста температуры ∆T от тока I печатной дорожки шириной w и толщиной фольги h, приведённая Д.Бруксом в [1]:
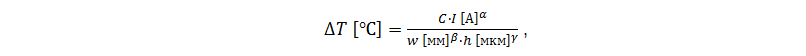
где C, α, β, γ – константы, значения которых для внешних и внутренних слоёв приведены в таблице 1. Стоит учитывать, что на внешних слоях толщина фольги обычно больше на 20-40 мкм относительно базового значения в связи с дополнительным напылением при создании переходных отверстий. Также влияние финишного покрытия на платах без маски может быть значительным. Это используют в силовых приборах, когда на вскрытую от маски печатную дорожку паяют дополнительный припой.
Ещё одной известной формулой расчёта предельной токонесущей способности проводника является формула Ондердонка (англ. I.M.Onderdonk), которая содержит такой важный параметр, как время. Она связывает время t пропускания тока I через медный проводник сечением S и прирост температуры ∆T относительно начальной температуры T0:

Так как при выводе формулы [2] исключается всякий теплоотвод, то для случая печатной дорожки эта формула применима для короткого импульса тока длительностью до 1-2 секунд. С увеличением времени и влияния теплоотвода точность оценки падает, в разы занижая предельный ток. Графики зависимостей по всем трём приведённым формулам для различных параметров печатной дорожки приведены на рисунках 1 и 2.

Всегда важно учитывать условия эксперимента или аналитические допущения при выводе, чтобы понимать границы применимости той или иной формулы. Ни одна из приведённых формул не даст точное и оптимальное соотношение между предельным током и требуемым сечением проводника для реальных приложений. Это же касается и простых калькуляторов, которые можно найти в сети Интернет (например), потому что они основаны на этих или аналогичных формулах. Влияние соседних проводников и компонентов как источников и приемников тепла, излучения, активного или пассивного охлаждения может быть учтено только при термоэлектрическом моделировании в специализированных САПР (таких как Cadence, ANSYS и других). Однако даже в этом случае результаты моделирования и эксперимента могут значительно отличаться. Дело в том, что печатная дорожка имеет не прямоугольное сечение, а близкое к трапециевидному (рис. 3), а её ширина и значение проводимости медной фольги могут не только отличаются от расчётных по модели, но и имеют некоторый разброс от образца к образцу, партии к партии, изготовителю к изготовителю и т.д. Влияние отклонений ширины усиливается с её уменьшением. Тем не менее, расчётные результаты по формулам и рекомендации стандартов чаще всего будут представлять наихудший случай, обеспечивая тем самым запас прочности системы. Если разработчику требуется оптимизировать соотношение между предельным током и требуемым сечением печатной дорожки, то к этой цели необходимо идти итеративным путём моделирования и эксперимента.

Скин-эффект
Увеличение сечения печатной дорожки пропорционально снижает её омическое сопротивление на единицу длины, что уменьшает тепловые потери при протекании постоянного тока. Ситуация с переменным током не так проста по причине существования скин-эффекта (англ. skin effect), который приводит к тому, что плотность переменного тока неравномерно распределена по сечению проводника, экспоненциально убывая до нуля от поверхности проводника к центру. Для удобства расчётов применяется понятие эффективного сечения проводника с глубиной, определяемой соотношением:
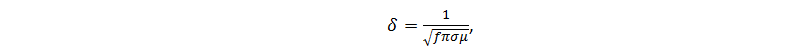
где f – частота тока, σ – проводимость металла, μ – магнитная проницаемость. На глубине равной δ плотность тока становится меньше в e раз относительно плотности тока на поверхности JS. Математически можно показать верность следующего приближённого равенства для плотности тока J(x,y) в проводнике:
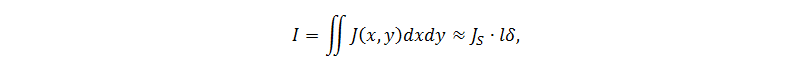
То есть для приближённых вычислений можно принять, что ток течёт только в граничном слое проводника периметра l глубиной δ, причём с равномерным распределением (рис. 4).

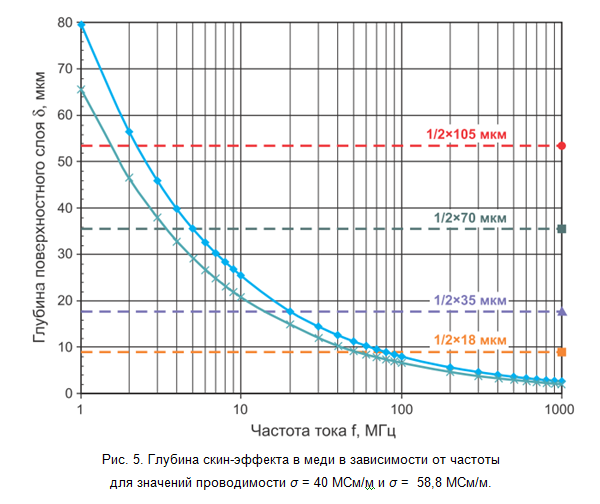
В рамках этой упрощённой модели, если глубина поверхностного слоя меньше половины толщины печатной дорожки, то импеданс печатной дорожки на данной частоте будет определяться именно этим эффективным сечением, приводя к увеличению омического сопротивления и незначительному снижению индуктивности. На рис. 5 представлена зависимость глубины поверхностного слоя от частоты тока с учётом разброса проводимости осаждённой меди. Из него видно, что для слоёв меди толщиной 18 мкм граничная частота (выше которой скин-эффект играет роль) находится в районе 50-70 МГц, а для слоёв толщиной 35 мкм – в районе 15-20 МГц. Отметим, что на частотах свыше 100 МГц глубина скин-эффекта меняется незначительно, это позволяет пренебрегать его зависимостью от частоты при расчётах для высокочастотных сигналов.
При проектировании печатных плат с постоянно действующими токами величиной в несколько ампер необходимо выполнять тепловые расчёты как для электрических компонентов, так и для проводников. Представленные модели и аналитические соотношения позволяют выполнить оценку предельного тока печатных дорожек и на её основании выбрать необходимую толщину медных слоёв и топологию проводников. Для получения точного решения необходимо использовать специализированные САПР, при этом желательно задавать геометрию с учётом технологических погрешностей изготовления и данные по проводимости меди, полученные от производителя печатных плат. Очень рекомендую ознакомиться со статьями Д.Брукса, посвящёнными подробному анализу методов оценки температуры печатных проводников, где представлены наглядные результаты моделирования температурных полей.
Литература
[1] Brooks D. G., Adam J. «Trace Currents and Temperatures Revisited», UltraCAD, 2015.
[2] Adam J., Brooks D. G. «In Search For Preece and Onderdonk», UltraCAD, 2015.
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №1. Публикация на «Geektimes» согласована с редакцией журнала.