Деление — одна из самых дорогих операций в современных процессорах. За доказательством далеко ходить не нужно: Agner Fog[1] вещает, что на процессорах Intel / AMD мы легко можем получить Latency в 25-119 clock cycles, а reciprocal throughput — 25-120. В переводе на Русский — МЕДЛЕННО! Тем не менее, возможность избежать инструкции деления в вашем коде — есть. И в этой статье, я расскажу как это работает, в частности в современных компиляторах(они то, умеют так уже лет 20 как), а также, расскажу как полученное знание можно использовать для того чтобы сделать код лучше, быстрее, мощнее.
Собственно, я о чем: если делитель известен на этапе компиляции, есть возможность заменить целочисленное деление умножением и логическим сдвигом вправо (а иногда, можно обойтись и без него вовсе — я конечно про реализацию в Языке Программирования). Звучит весьма обнадеживающе: операция целочисленного умножения и сдвиг вправо на, например, Intel Haswell займут не более 5 clock cycles. Осталось лишь понять, как, например, выполняя целочисленное деление на 10, получить тот же результат целочисленным умножением и логическим сдвигом вправо? Ответ на этот вопрос лежит через понимание… Fixed Point Arithmetic (далее FPA). Чуть-чуть основ.
При использовании FP, экспоненту (показатель степени 2 => положение точки в двоичном представлении числа) в числе не сохраняют (в отличие от арифметики с плавающей запятой, см. IEE754), а полагают ее некой оговоренной, известной программистам величиной. Сохраняют же, только мантиссу (то, что идёт после запятой). Пример:
0.1 — в двоичной записи имеет 'бесконечное представление', что в примере выше отмечено круглыми скобками — именно эта часть будет повторяться от раза к разу, следуя друг за другом в двоичной FP записи числа 0.1.
В примере выше, если мы используем для хранения FP чисел 16-битные регистры, мы не сможем уместить FP представление числа 0.1 в такой регистр не потеряв в точности, а это в свою очередь скажется на результате всех дальнейших вычислений в которых значение этого регистра участвует.
Пусть дано 16-битное целое число A и 16-битная Fraction часть числа B. Произведение A на B результатом дает число с 16 битами в целой части и 16-тью битами в дробной части. Чтобы получить только целую часть, очевидно, нужно сдвинуть результат на 16 бит вправо.
Поздравляю, вводная часть в FPA окончена.
Формируем следующую гипотезу: для выполнения целочисленного деления на 10, нам нужно выполнить умножение Числа Делимого на FP представление числа 0.1, взять целую часть и дело в шля… минуточку… А будет ли полученный результат точным, точнее его целая часть? — Ведь, как мы помним, в памяти у нас хранится лишь приближенная версия числа 0.1. Ниже я выписал три различных представления числа 0.1: бесконечно точное представление числа 0.1, обрезанное после 16-ого бита без округления представление числа 0.1 и обрезанное после 16 ого бита с округлением вверх представление числа 0.1.
Оценим погрешности truncating представлений числа 0.1:
Чтобы результат умножения целого числа A, на Аппроксимацию числа 0.1 давал точную целую часть, нам нужно чтобы:
Удобнее использовать первое выражение: при
Внимательно смотрим на двоичное представление — truncating with rounding up 0.1: старшие три бита — нулевые, а значит, и никакого вклада в результат умножения не вносят (новых бит).
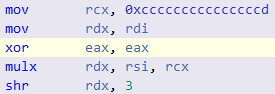
Следовательно, мы можем сдвинуть наше число влево на три бита, выполнить округление вверх и, выполнив умножение и логический сдвиг вправо сначала на 16, а затем на 3 (то есть, за один раз на 19 вообще говоря) — получим нужную, точную целую часть. Доказательство корректности такого '19' битного умножения аналогично предыдущему, с той лишь разницей, что для 16-битных чисел оно работает правильно. Аналогичные рассуждения верны и для чисел большей разрядности, да и не только для деления на 10.
Ранее я писал, что вообще говоря, можно обойтись и без какого-либо сдвига вовсе, ограничившись лишь умножением. Как? Ассемблер x86 / x64 на барабане:
В современных процессорах, есть команда MUL (есть еще аналоги IMUL, MULX — BMI2), которая принимая один, скажем 32 / 64 -битный параметр, способна выполнять 64 / 128 битное умножение, сохраняя результат частями в два регистра (старшие 32 / 64 бита и младшие, соответственно):
MUL RCX ; умножить RCX на RAX, а результат (128 бит) сохранить в RDX:RAXВ регистре RCX пусть хранится некое целое 62-битное A, а в регистре RAX пускай хранится 64 битное FA представление truncating with rounding up числа 0.1 (заметь, никаких сдвигов влево нету). Выполнив 64-битное умножение получим, что в регистре RDX сохранятся старшие 64 бита результата, или, точнее говоря — целая часть, которая для 62 битных чисел, будет точной. То есть, сдвиг вправо (SHR, SHRX) не нужен. Наличие же такого сдвига нагружает Pipeline процессора, вне зависимости поддерживает ли он OOOE или нет: как минимум появляется лишняя зависимость в, скорее всего и без того длинной цепочке таких зависимостей (aka Dependency Chain). И вот тут, очень важно упомянуть о том, что современные компиляторы, видя выражение вида some_integer / 10 — автоматически генерируют ассемблерный код для всего диапазона чисел Делимого. То есть, если вам известно что числа у вас всегда 53-ех битные (в моей задаче именно так и было), то лишнюю инструкцию сдвига вы получите все равно. Но, теперь, когда вы понимаете как это работает, можете сами с легкостью заменить деление — умножением, не полагаясь на милость компилятору. К слову сказать, получение старших битов 64 битного произведения в C++ коде реализуется интринсиком (something like mulh), что по Asm коду, должно быть равносильно строчкам инструкции {I}MUL{X} выше.
Возможно, с появлением контрактов (в С++ 20 не ждем) ситуация улучшится, и в каких-то кейсах, мы сможем довериться машине! Хотя, это же С++, тут за все отвечает программист — не иначе.
Рассуждения описанные выше — применимы к любым делителям константам, ну а ниже список полезных ссылок:
[1] https://www.agner.org/optimize/instruction_tables.pdf
[2] Круче чем Агнер Фог
[3] Телеграмм канал, с полезной информацией о оптимизациях под Intel / AMD / ARM
[4] Про деление нацело, но по Английски