Представьте, если бы Земля была в форме куба. Как тогда найти кратчайший путь вокруг света?
Вы когда-нибудь задумывались, какой была жизнь, если бы Земля была не сферой, а имела другую форму? Мы воспринимаем как должное плавный ход нашей планеты по Солнечной системе и медленные закаты, которыми мы можем наслаждаться благодаря вращательной симметрии Земли. Кроме того, сферическая Земля позволяет определить и самый быстрый способ добраться из точки A в точку B: просто пройдите по кругу, который проходит через эти две точки и разрезает сферу пополам. Мы используем такие кратчайшие пути, их называют геодезическими, для планирования маршрутов самолетов и для расчета спутниковых орбит.

Но что бы произошло, если бы мы жили на кубе? Наш мир раскачивало бы больше, горизонты искривлены, а кратчайший путь из точки А в точку B найти труднее. Возможно, вы и не будете тратить много времени, чтобы представить свою жизнь на кубе, но математики будут: они изучают, как бы выглядели наши путешествия на самых разных формах. А недавнее решение одного из фундаментальных вопросов о додекаэдре вообще изменило взгляд на объект, который находится у нас перед глазами уже тысячи лет.
Поиск самого короткого пути туда и обратно (из одной точки обратно в эту же точку вокруг куба) для данного геометрического тела может показаться простой задачей. В конце концов, вы же точно вернетесь к тому месту, откуда начали, верно?
На самом деле, это зависит от фигуры или тела, по которому вы идете. Если это сфера, то да. (И да, мы опускаем тот факт, что Земля не является идеальной сферой, а ее поверхность не совсем гладкая.) На сфере пути по прямой повторяют «большие круги», геодезические, например, экватор. Если вы обойдете экватор, то примерно через 25 000 миль вы сделаете полный круг и вернетесь туда, откуда начали.
В кубическом мире геодезические линии не так очевидны. Найти прямой путь на одной грани легко, поскольку каждая грань плоская. Но если бы вы ходили по кубическому миру вокруг, как бы вы продолжали идти прямо, когда достигали края?
Есть старая забавная математическая задача, которая иллюстрирует ответ на наш вопрос. Представьте себе муравья в одном из углов куба, который хочет добраться до противоположного угла. Каков кратчайший путь на поверхности куба от точки A до точки B?
Представьте множество разных путей, по которым может идти муравей.
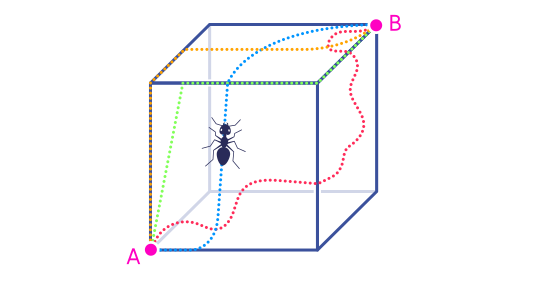
Но какой из них самый короткий? Есть гениальный способ решения проблемы. Расплющим куб!
Если бы куб был сделан из бумаги, вы могли бы разрезать его вдоль ребер и разгладить лист, чтобы получить такую развертку.
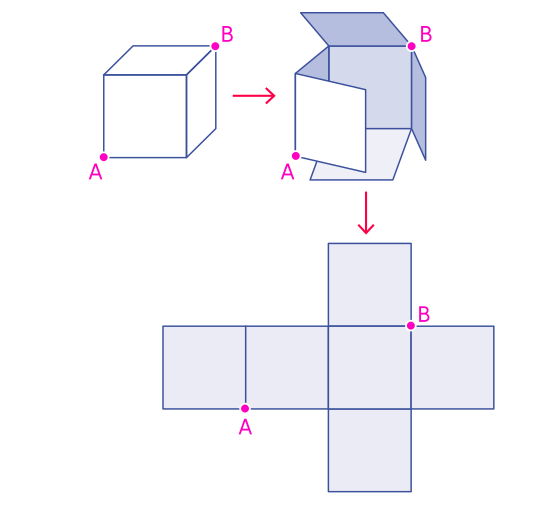
В таком плоском мире легко найти кратчайший путь от A до B: просто проведите прямую линию между ними.

Чтобы увидеть, какой будет геодезическая линия в кубомире, просто соберите куб обратно. Вот наш кратчайший путь.
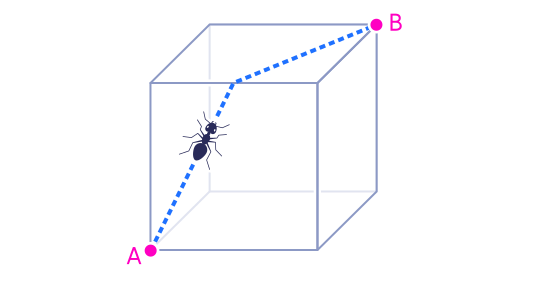
“Выравнивание” куба работает, потому что каждая грань куба плоская, поэтому ничего не искажается, когда мы разворачиваем тело вдоль ребер. (Подобная попытка «развернуть» сферу не сработает, поскольку мы не можем сделать сферу плоской, не искажая ее.)
Теперь, когда у нас есть представление о том, как выглядят пути по прямой на кубе, давайте вернемся к вопросу, можем ли мы пройти по любому прямому пути и в конечном итоге вернуться туда, откуда начали. В отличие от сферы, на кубе не каждый прямой путь возвращает нас обратно на старт.
Но подобные маршруты туда и обратно возможны. С одной уловкой! Обратите внимание, что муравей может продолжить путь, обозначенный нами выше, и вернуться туда, где начал. На кубе полный круг создает путь, больше похожий на ромб.

Следуя по этому пути (туда и обратно), муравей должен пройти через другую вершину (точку B), прежде чем вернуться в свою начальную точку. В этом и заключается загвоздка: каждый прямой путь, который начинается и заканчивается в одной и той же вершине, должен проходить через другую вершину куба.
Оказывается, это верно для четырех из пяти платоновых тел. В кубе, тетраэдре, октаэдре и икосаэдре любой прямой путь, который начинается и заканчивается в одной и той же вершине, должен проходить через какую-то другую вершину по пути. Математики доказали это пять лет назад, но додекаэдра в их списке не было. Мы вернемся к этому чуть позже.

Чтобы понять, почему этот факт о геодезических верен для четырех из пяти платоновых тел, мы воспользуемся методом «кувырка» (tumbling) и переключимся на тетраэдрический мир, где этот способ можно нагляднее продемонстрировать.
Представьте, что вы начинаете путь с вершины тетраэдра и идете по прямой вдоль грани. Расположим тетраэдр так, чтобы путь начинался с нижней грани.
Когда мы встречаем ребро, мы переворачиваем тетраэдр так, чтобы наш путь продолжался по грани, которая оказывается снизу:

Такие повороты дают возможность отслеживать наш путь так же, как мы это делали бы по развертке куба:

Траектория вращений выше представляет этот путь на поверхности тетраэдра:

Пять поворотов тетраэдра соответствуют дополнительным пяти граням, пересеченным нашим маршрутом.
Теперь мы можем представить любой путь на поверхности тетраэдра как путь в этом «вращающемся» пространстве. Давайте определим нашу отправную точку А и посмотрим, где она окажется после нескольких поворотов.
Когда наш путь выходит из точки A, тетраэдр падает на противоположную сторону. Это поднимает точку A от земли.
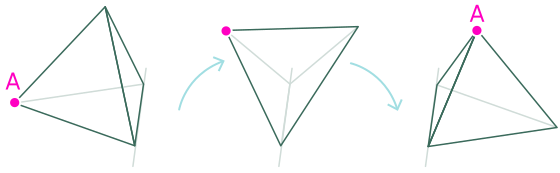
Вершина A временно возвышается в нашем вращающемся мире. Обычно мы не указываем местоположение точки А при создании нашего вращающегося пространства, но вот где она могла бы появиться, если бы мы смотрели вниз.

По мере того как наш путь продолжается, тетраэдр снова падает. Он может это сделать в одном из двух возможных направлений, но в любом случае А снова оказывается внизу.

Когда мы заставляем тетраэдр падать во всех возможных направлениях, мы получаем кувырок, который выглядит следующим образом:

Получается своеобразная решетка из-за того, что равносторонние треугольные грани тетраэдра совпадают друг с другом.

Эта сетка из треугольников говорит нам о двух интересных вещах в нашем вращающемся мире. Во-первых, все точки, в которые могут приземлиться вершины тетраэдра, являются «точками решетки» (показано на схеме) или точками с целыми координатами. Это потому, что одна единица в нашей системе координат равна длине одного ребра тетраэдра.
Во-вторых, посмотрите, где может оказаться A.

Координаты A всегда четные. Всякий раз, когда A оказывается внизу, она возвращается туда же спустя два вращения, поэтому все возможные места приземления для A размещены с интервалом в две длины ребра на каждом направлении вращения.
Теперь посмотрим, что это говорит о геодезических линиях. Напомним, что путь в тетраэдре, который начинается и заканчивается в точке A, будет отрезком прямой линии во вращающемся пространстве, с началом в точке A (0,0) и с концом в другой точке A. А когда начальная и конечная точки пути совпадают в единой А, что будет в середине пути?
Даже в нашей запутанной системе координат стандартная формула для вычисления середины отрезка все еще работает, поэтому мы можем найти ее координаты, исходя из координат конечных точек.
Поскольку обе координаты начальной точки равны 0, а обе координаты конечной точки четные, координаты середины являются целыми числами. То есть середина будет одной из точек решетки, а, как мы заметили выше, это значит, что она соответствует вершине треугольника во вращающемся пространстве.
Например, путь из (0,0) в (4,2) имеет середину (2,1), это отмеченная точка решетки в нашей сетке.

Получается, что на поверхности тетраэдра путь от A и обратно должен проходить через другую вершину.
Поскольку каждое возможное “место приземления” для A имеет четные координаты, середина каждого геодезического пути, начинающегося и заканчивающегося в A, будет соответствовать точке решетки. Это доказывает, что каждая геодезическая линия от A до A на поверхности тетраэдра должна проходить через другую вершину.
Это простая аргументация была тщательно разработана в 2015 году математиками Дайаной Дэвис, Виктором Додс, Синтией Трауб и Джедом Янг.
Они использовали аналогичный, но гораздо более сложный метод, чтобы доказать то же самое для куба. В следующем году Дмитрий Фукс подтвердил результаты для октаэдра и икосаэдра. Благодаря этому, мы знаем, что для тетраэдра, куба, октаэдра и икосаэдра нет прямых путей, идущих от вершины обратно к самой себе, которые бы не проходили через другую вершину.
Но вопрос о существовании таких путей на поверхности додекаэдра оставался открытым до 2019 года, когда математики Джаядев Атрейя, Дэвид Авликино и Патрик Хупер доказали, что это действительно возможно. Фактически они нашли бесконечно много прямых путей на поверхности додекаэдра, которые начинаются и заканчиваются в одной и той же вершине, не проходя через другие.
Вот один из них, изображенный на развертке додекаэдра, прячущийся у всех на виду.

Тысячи лет платоновы тела изучались вместе, ведь у них так много общего. Но теперь мы знаем кое-что новое о додекаэдре, и это явно отличает его от других тел.
Данное загадочное открытие показывает, что независимо от того, насколько хорошо мы понимаем математические объекты, нам всегда есть чему поучиться. Важно помнить, что путь от проблемы к ее решению не всегда будет прямой!
1. Если длина ребра куба равна 1, какова кратчайшая длина пути муравья от одной вершины до противоположной?
2. Объясните, почему приведенная ниже схема не может быть траекторией вращения на кубе.
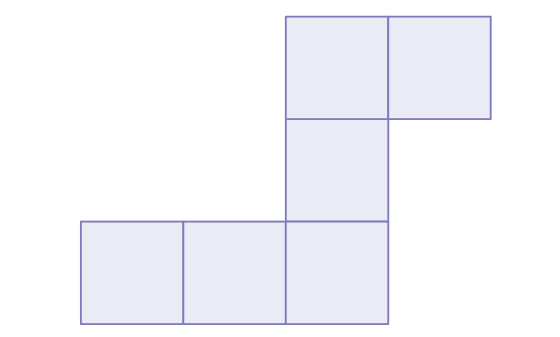
3. Одна из сложностей во «вращении» куба заключается в том, что точка A не имеет уникального конечного положения, связанного с конечным положением куба. Например, даже если куб оказывается в одном и том же месте, вращаясь по красному или по синему пути, точка А оказывается в разных положениях. Определите, где окажется А после поворотов по красной и синей траектории.

4. Это траектория поворотов куба.
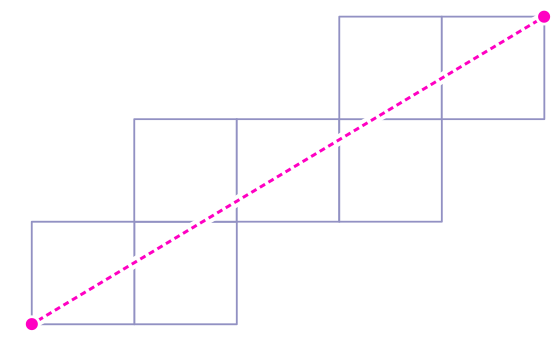
Нарисуйте путь на поверхности куба, начиная с точки A.

Вы когда-нибудь задумывались, какой была жизнь, если бы Земля была не сферой, а имела другую форму? Мы воспринимаем как должное плавный ход нашей планеты по Солнечной системе и медленные закаты, которыми мы можем наслаждаться благодаря вращательной симметрии Земли. Кроме того, сферическая Земля позволяет определить и самый быстрый способ добраться из точки A в точку B: просто пройдите по кругу, который проходит через эти две точки и разрезает сферу пополам. Мы используем такие кратчайшие пути, их называют геодезическими, для планирования маршрутов самолетов и для расчета спутниковых орбит.

Но что бы произошло, если бы мы жили на кубе? Наш мир раскачивало бы больше, горизонты искривлены, а кратчайший путь из точки А в точку B найти труднее. Возможно, вы и не будете тратить много времени, чтобы представить свою жизнь на кубе, но математики будут: они изучают, как бы выглядели наши путешествия на самых разных формах. А недавнее решение одного из фундаментальных вопросов о додекаэдре вообще изменило взгляд на объект, который находится у нас перед глазами уже тысячи лет.
Поиск самого короткого пути туда и обратно (из одной точки обратно в эту же точку вокруг куба) для данного геометрического тела может показаться простой задачей. В конце концов, вы же точно вернетесь к тому месту, откуда начали, верно?
На самом деле, это зависит от фигуры или тела, по которому вы идете. Если это сфера, то да. (И да, мы опускаем тот факт, что Земля не является идеальной сферой, а ее поверхность не совсем гладкая.) На сфере пути по прямой повторяют «большие круги», геодезические, например, экватор. Если вы обойдете экватор, то примерно через 25 000 миль вы сделаете полный круг и вернетесь туда, откуда начали.
В кубическом мире геодезические линии не так очевидны. Найти прямой путь на одной грани легко, поскольку каждая грань плоская. Но если бы вы ходили по кубическому миру вокруг, как бы вы продолжали идти прямо, когда достигали края?
Есть старая забавная математическая задача, которая иллюстрирует ответ на наш вопрос. Представьте себе муравья в одном из углов куба, который хочет добраться до противоположного угла. Каков кратчайший путь на поверхности куба от точки A до точки B?
Представьте множество разных путей, по которым может идти муравей.

Но какой из них самый короткий? Есть гениальный способ решения проблемы. Расплющим куб!
Если бы куб был сделан из бумаги, вы могли бы разрезать его вдоль ребер и разгладить лист, чтобы получить такую развертку.

В таком плоском мире легко найти кратчайший путь от A до B: просто проведите прямую линию между ними.

Чтобы увидеть, какой будет геодезическая линия в кубомире, просто соберите куб обратно. Вот наш кратчайший путь.

“Выравнивание” куба работает, потому что каждая грань куба плоская, поэтому ничего не искажается, когда мы разворачиваем тело вдоль ребер. (Подобная попытка «развернуть» сферу не сработает, поскольку мы не можем сделать сферу плоской, не искажая ее.)
Теперь, когда у нас есть представление о том, как выглядят пути по прямой на кубе, давайте вернемся к вопросу, можем ли мы пройти по любому прямому пути и в конечном итоге вернуться туда, откуда начали. В отличие от сферы, на кубе не каждый прямой путь возвращает нас обратно на старт.
Но подобные маршруты туда и обратно возможны. С одной уловкой! Обратите внимание, что муравей может продолжить путь, обозначенный нами выше, и вернуться туда, где начал. На кубе полный круг создает путь, больше похожий на ромб.

Следуя по этому пути (туда и обратно), муравей должен пройти через другую вершину (точку B), прежде чем вернуться в свою начальную точку. В этом и заключается загвоздка: каждый прямой путь, который начинается и заканчивается в одной и той же вершине, должен проходить через другую вершину куба.
Оказывается, это верно для четырех из пяти платоновых тел. В кубе, тетраэдре, октаэдре и икосаэдре любой прямой путь, который начинается и заканчивается в одной и той же вершине, должен проходить через какую-то другую вершину по пути. Математики доказали это пять лет назад, но додекаэдра в их списке не было. Мы вернемся к этому чуть позже.

Чтобы понять, почему этот факт о геодезических верен для четырех из пяти платоновых тел, мы воспользуемся методом «кувырка» (tumbling) и переключимся на тетраэдрический мир, где этот способ можно нагляднее продемонстрировать.
Представьте, что вы начинаете путь с вершины тетраэдра и идете по прямой вдоль грани. Расположим тетраэдр так, чтобы путь начинался с нижней грани.
Когда мы встречаем ребро, мы переворачиваем тетраэдр так, чтобы наш путь продолжался по грани, которая оказывается снизу:

Такие повороты дают возможность отслеживать наш путь так же, как мы это делали бы по развертке куба:

Траектория вращений выше представляет этот путь на поверхности тетраэдра:

Пять поворотов тетраэдра соответствуют дополнительным пяти граням, пересеченным нашим маршрутом.
Теперь мы можем представить любой путь на поверхности тетраэдра как путь в этом «вращающемся» пространстве. Давайте определим нашу отправную точку А и посмотрим, где она окажется после нескольких поворотов.
Когда наш путь выходит из точки A, тетраэдр падает на противоположную сторону. Это поднимает точку A от земли.

Вершина A временно возвышается в нашем вращающемся мире. Обычно мы не указываем местоположение точки А при создании нашего вращающегося пространства, но вот где она могла бы появиться, если бы мы смотрели вниз.

По мере того как наш путь продолжается, тетраэдр снова падает. Он может это сделать в одном из двух возможных направлений, но в любом случае А снова оказывается внизу.
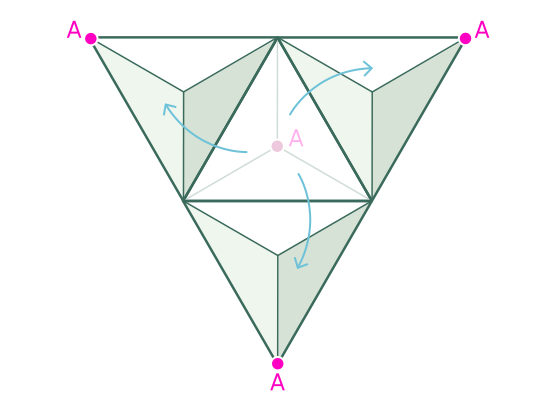
Когда мы заставляем тетраэдр падать во всех возможных направлениях, мы получаем кувырок, который выглядит следующим образом:

Получается своеобразная решетка из-за того, что равносторонние треугольные грани тетраэдра совпадают друг с другом.

Эта сетка из треугольников говорит нам о двух интересных вещах в нашем вращающемся мире. Во-первых, все точки, в которые могут приземлиться вершины тетраэдра, являются «точками решетки» (показано на схеме) или точками с целыми координатами. Это потому, что одна единица в нашей системе координат равна длине одного ребра тетраэдра.
Во-вторых, посмотрите, где может оказаться A.
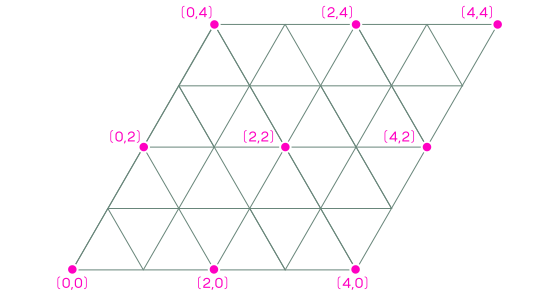
Координаты A всегда четные. Всякий раз, когда A оказывается внизу, она возвращается туда же спустя два вращения, поэтому все возможные места приземления для A размещены с интервалом в две длины ребра на каждом направлении вращения.
Теперь посмотрим, что это говорит о геодезических линиях. Напомним, что путь в тетраэдре, который начинается и заканчивается в точке A, будет отрезком прямой линии во вращающемся пространстве, с началом в точке A (0,0) и с концом в другой точке A. А когда начальная и конечная точки пути совпадают в единой А, что будет в середине пути?
Даже в нашей запутанной системе координат стандартная формула для вычисления середины отрезка все еще работает, поэтому мы можем найти ее координаты, исходя из координат конечных точек.
Поскольку обе координаты начальной точки равны 0, а обе координаты конечной точки четные, координаты середины являются целыми числами. То есть середина будет одной из точек решетки, а, как мы заметили выше, это значит, что она соответствует вершине треугольника во вращающемся пространстве.
Например, путь из (0,0) в (4,2) имеет середину (2,1), это отмеченная точка решетки в нашей сетке.

Получается, что на поверхности тетраэдра путь от A и обратно должен проходить через другую вершину.
Поскольку каждое возможное “место приземления” для A имеет четные координаты, середина каждого геодезического пути, начинающегося и заканчивающегося в A, будет соответствовать точке решетки. Это доказывает, что каждая геодезическая линия от A до A на поверхности тетраэдра должна проходить через другую вершину.
Это простая аргументация была тщательно разработана в 2015 году математиками Дайаной Дэвис, Виктором Додс, Синтией Трауб и Джедом Янг.
Они использовали аналогичный, но гораздо более сложный метод, чтобы доказать то же самое для куба. В следующем году Дмитрий Фукс подтвердил результаты для октаэдра и икосаэдра. Благодаря этому, мы знаем, что для тетраэдра, куба, октаэдра и икосаэдра нет прямых путей, идущих от вершины обратно к самой себе, которые бы не проходили через другую вершину.
Но вопрос о существовании таких путей на поверхности додекаэдра оставался открытым до 2019 года, когда математики Джаядев Атрейя, Дэвид Авликино и Патрик Хупер доказали, что это действительно возможно. Фактически они нашли бесконечно много прямых путей на поверхности додекаэдра, которые начинаются и заканчиваются в одной и той же вершине, не проходя через другие.
Вот один из них, изображенный на развертке додекаэдра, прячущийся у всех на виду.

Тысячи лет платоновы тела изучались вместе, ведь у них так много общего. Но теперь мы знаем кое-что новое о додекаэдре, и это явно отличает его от других тел.
Данное загадочное открытие показывает, что независимо от того, насколько хорошо мы понимаем математические объекты, нам всегда есть чему поучиться. Важно помнить, что путь от проблемы к ее решению не всегда будет прямой!
Задания
1. Если длина ребра куба равна 1, какова кратчайшая длина пути муравья от одной вершины до противоположной?
2. Объясните, почему приведенная ниже схема не может быть траекторией вращения на кубе.

3. Одна из сложностей во «вращении» куба заключается в том, что точка A не имеет уникального конечного положения, связанного с конечным положением куба. Например, даже если куб оказывается в одном и том же месте, вращаясь по красному или по синему пути, точка А оказывается в разных положениях. Определите, где окажется А после поворотов по красной и синей траектории.

4. Это траектория поворотов куба.
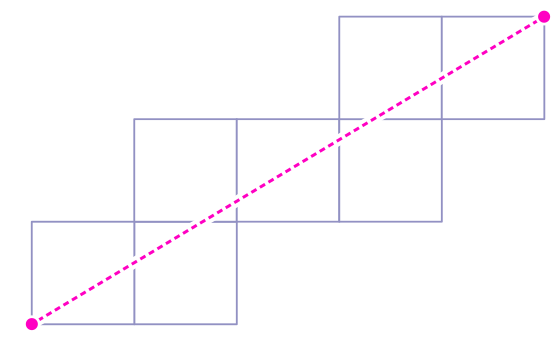
Нарисуйте путь на поверхности куба, начиная с точки A.

Ответы
Нажмите, чтобы увидеть ответ 1
Путь — это гипотенуза прямоугольного треугольника с катетами длиной 1 и 2.
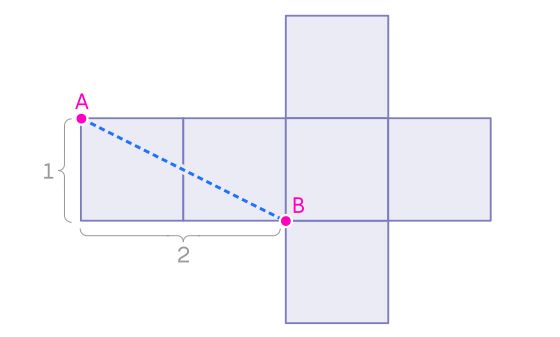
Согласно теореме Пифагора, длина AB равна √5.

Согласно теореме Пифагора, длина AB равна √5.
Нажмите, чтобы увидеть ответ 2
Если данная траектория заставляет куб сначала поворачиваться дважды вправо, то его наклон составляет не более 1 куба вверх. После первого кувырка наверх, наивысшая точка достигает середину стороны, что вынуждает нас сделать следующий поворот направо.

Это дает некоторое представление о том, почему траектории «кувырка» у куба сложнее, чем у тетраэдра.

Это дает некоторое представление о том, почему траектории «кувырка» у куба сложнее, чем у тетраэдра.
Нажмите, чтобы увидеть ответ 3
Будет полезно повторить это кубиком Рубика или игральным кубиком.
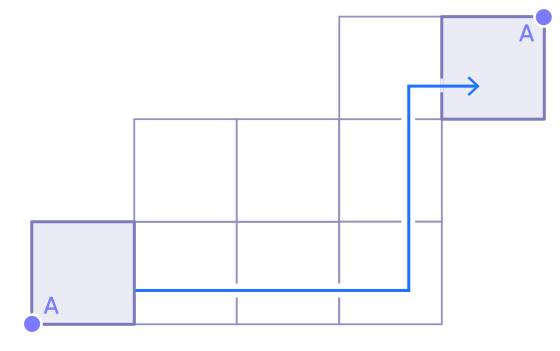

Обратите также внимание, что синий маршрут не может быть траекторией вращения для указанного пути на кубе.
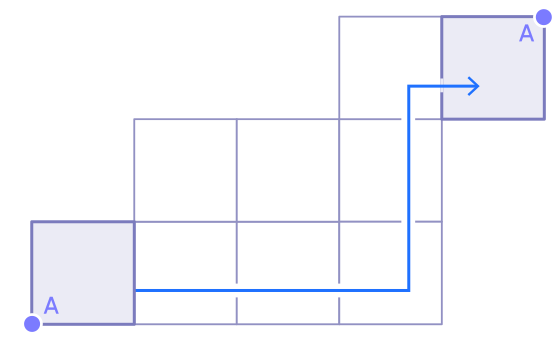

Обратите также внимание, что синий маршрут не может быть траекторией вращения для указанного пути на кубе.
Нажмите, чтобы увидеть ответ 4

