
👾, Хабр!
На прошлых неделях мы познакомились с различными вариациями альтернативных окрестностей – начиная с учёта расположения нотацией Хенселя, через альтернативные шаблоны расположения, и заканчивая взвешенными окрестностями. Сегодня добавим в тему окрестностей стандартного поля небольшой финальный штрих – пользовательские расположения.
Что здесь происходит (для новых читателей серии)
В этой серии мы разбираем клеточные автоматы – дискретную модель, основой которой является сетка из ячеек-клеток, которые изменяют (или не изменяют) своё состояние в зависимости от количества соседей.
Учёт соседей определяется правилами, которые устанавливаются нами. Вариаций правил существует бесчисленное множество, и они были систематизированы в определённые конфигурации.
Самая популярная конфигурация – «B/S», или «life-like», по названию крайне широко известного клеточного автомата «Game of Life», где B/S обозначает, что в нашем правиле мы описываем всего два параметра – количество соседей необходимых для рождения новой клетки в пустой ячейке, и количество соседей для выживания существующей клетки.
В каждой статье серии мы углубляемся в данную конфигурацию, добавляя новые параметры, либо дополняя существующие. Иногда заглядываем и в прочие конфигурации.
Для понимания сегодняшней статьи достаточно знать, что:
Учёт соседей определяется правилами, которые устанавливаются нами. Вариаций правил существует бесчисленное множество, и они были систематизированы в определённые конфигурации.
Самая популярная конфигурация – «B/S», или «life-like», по названию крайне широко известного клеточного автомата «Game of Life», где B/S обозначает, что в нашем правиле мы описываем всего два параметра – количество соседей необходимых для рождения новой клетки в пустой ячейке, и количество соседей для выживания существующей клетки.
В каждой статье серии мы углубляемся в данную конфигурацию, добавляя новые параметры, либо дополняя существующие. Иногда заглядываем и в прочие конфигурации.
Для понимания сегодняшней статьи достаточно знать, что:
- поиск соседей изначально выполняется в радиусе 1 (8 окружающих клеток –
 ), но мы можем установить другой, добавив к правилу Rx, где x – нужный нам радиус;
), но мы можем установить другой, добавив к правилу Rx, где x – нужный нам радиус; - мы можем изменять шаблон окрестности поиска соседей. Изначально подразумевается окрестность Мура – R в каждую сторону (и диагональ) от рассматриваемой клетки, – но указывая Nxx мы будем определять иной шаблон, что, конечно, изменит вид правила. Сегодня мы продолжаем расширение этой части правила. Знакомство с предыдущими расширениями не является необходимым, но вы, конечно, можете предварительно ознакомиться с ними и прочими дополнениями, для большей последовательности чтения. Ссылки в конце материала и в профиле.
Пользовательские окрестности можно разделить на два типа – ручные расположения и шаблоны построения. Начнём с первых.
❯ Ручные расположения
Данный тип поддерживаeтся в нотации через параметр окрестности
N@x, где x – код нашего расположения, составленный по определённым правилам:- Мы строим наше расположение в одномерном виде, последовательно указывая нулями и единицами учёт каждой клетки окрестности. К примеру, окрестность фон Неймана для радиуса 2 будет выглядеть как
00100 01110 11c11 01110 00100(пробелы для читаемости, построение происходит без них); - Убираем центральную клетку c, в данном варианте она никогда не учитывается (только если конфигурация/реализация не поддерживает параметр M в правиле, но к параметру окрестности он всё равно не относится);
- Переводим получившееся двоичное число в шестнадцатеричную систему счисления. Всё, код для нотации готов. Для примера с окрестностью фон Неймана и R2 это будет
N@23BDC4.
Это, конечно, куда короче изначального вида и родственного варианта обозначения во взвешенных окрестностях, но за это мы жертвуем наглядностью. Чтобы понять, какая окрестность скрывается за кодом, нам необходимо обратно развернуть изначальное представление окрестности. Тем не менее, именно этот вариант поддерживается в популярнейших симуляторах КА, и даже если вы создаёте собственный, вам тоже придётся поддерживать этот формат, что поделать. Или пользоваться нотацией взвешенных окрестностей, но с единичными весами. Тоже как вариант. Но перейдём к примерам.
Интереснее всего на пользовательских окрестностях смотрятся направленные варианты, построенные без интуитивно напрашивающейся полной симметрии.
R2/G2/S4-6,8-9/B6-9/N@839DE7
Или NW10000 01110 01011 01111 00111
:h Нотация
R – радиус поиска соседей. Регулирует окрестность.
G – количество состояний клеток. Минимум – 2 (жива/мертва), бо́льшие значения отвечают за длительность «старения» клетки, когда она уже не считается живым соседом для прочих клеток, но ещё не освободила клетку для рождения новой. Если совсем правильно, в HROT и LtL принято использовать C (Count of states).
M – булевый параметр, учитывается ли собственное состояние клетки при подсчёте соседей. В HROT данный параметр отсутствует (=всегда принимается за 0), но мы сохраним возможность использования этого параметра.
S – значения и/или диапазоны количества соседей, необходимых для выживания клетки. Диапазоны записываются через дефис (если учитывать обратную совместимость с LtL, может быть использовано двое- и троеточие или t), значения и диапазоны отделяются друг от друга запятыми.
B – полностью аналогично S, но отвечает за количество соседей, необходимых для рождения новой клетки.
N – обозначение используемой окрестности. Как раз об этом мы сегодня и говорим.
/ – разделитель между параметрами правила. В правильной нотации используются «,» (да, и между параметрами, и между диапазонами/значениями), но также встречается и вариант вовсе без разделителей между параметрами.
Характеристики примера – длительность анимации; [ускорение анимации от 100мс. на фрейм, если есть]; размер поля; размер и процент центрального заполнения на старте.
G – количество состояний клеток. Минимум – 2 (жива/мертва), бо́льшие значения отвечают за длительность «старения» клетки, когда она уже не считается живым соседом для прочих клеток, но ещё не освободила клетку для рождения новой. Если совсем правильно, в HROT и LtL принято использовать C (Count of states).
M – булевый параметр, учитывается ли собственное состояние клетки при подсчёте соседей. В HROT данный параметр отсутствует (=всегда принимается за 0), но мы сохраним возможность использования этого параметра.
S – значения и/или диапазоны количества соседей, необходимых для выживания клетки. Диапазоны записываются через дефис (если учитывать обратную совместимость с LtL, может быть использовано двое- и троеточие или t), значения и диапазоны отделяются друг от друга запятыми.
B – полностью аналогично S, но отвечает за количество соседей, необходимых для рождения новой клетки.
N – обозначение используемой окрестности. Как раз об этом мы сегодня и говорим.
/ – разделитель между параметрами правила. В правильной нотации используются «,» (да, и между параметрами, и между диапазонами/значениями), но также встречается и вариант вовсе без разделителей между параметрами.
Характеристики примера – длительность анимации; [ускорение анимации от 100мс. на фрейм, если есть]; размер поля; размер и процент центрального заполнения на старте.
В направленных окрестностях много очень простых, но забавных примеров. Как эти «капли на стекле»…

20с., 356×356, 300×20%
R2/G2/S1,3/B2,4/N@3C00
NW00000 00000 11011 00000 00000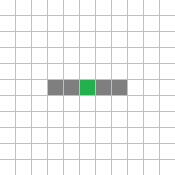
… просто линии (обратите внимание на корабли в верхней части примера)

25с., 356×356, 300×20%
R4/G3/S/B2/N@1018080000202
NW000000000 000000000 000000000 000010000 000101000 000010000 000000000 000000001 000000010
… обычные направленные корабли

47с., 178×178, 50×50%
R3/G3/S/B2/N@E1860001
NW0000000 0000000 0011100 0010100 0011000 0000000 0000001
… более сложные порождающие корабли-паровозы

49с., скорость ×1.5, 356×356, 50×50%
R2/G3/S0/B3/N@FFD9C4
NW11111 11111 01010 01110 00100

44с., 356×356, 3×100%
Продолжение

13с., 356×356, 3×100%

13с., 356×356, 3×100%
R1/G2/S2-3/B2-3/N@4D
NW010 001 101
… и многие другие структуры

18с., скорость ×1.5, 178×178, 50×20%
R2/G2/S0-3/B1-2/N@891891
NW10001 00100 01010 00100 10001 (а вот и FC)
Напоследок взглянем на более привычный, орнаментный вид.
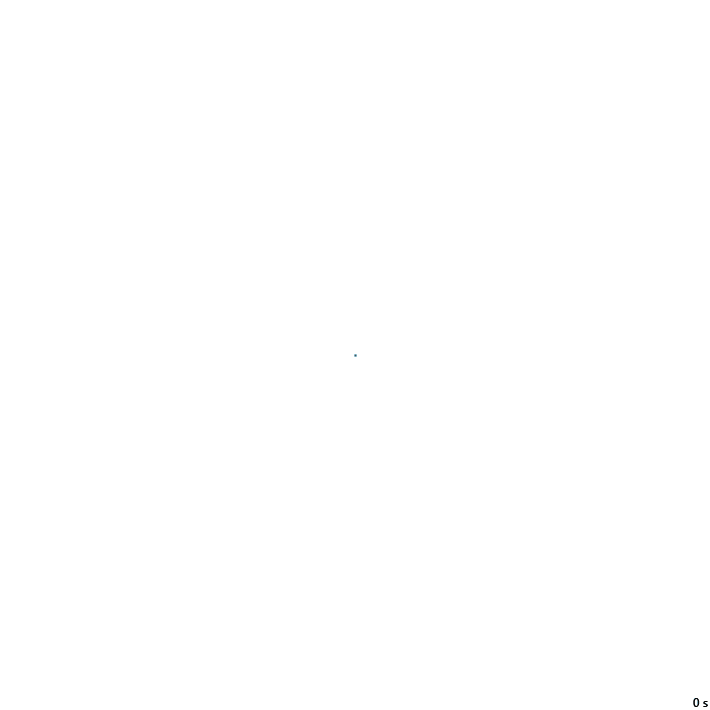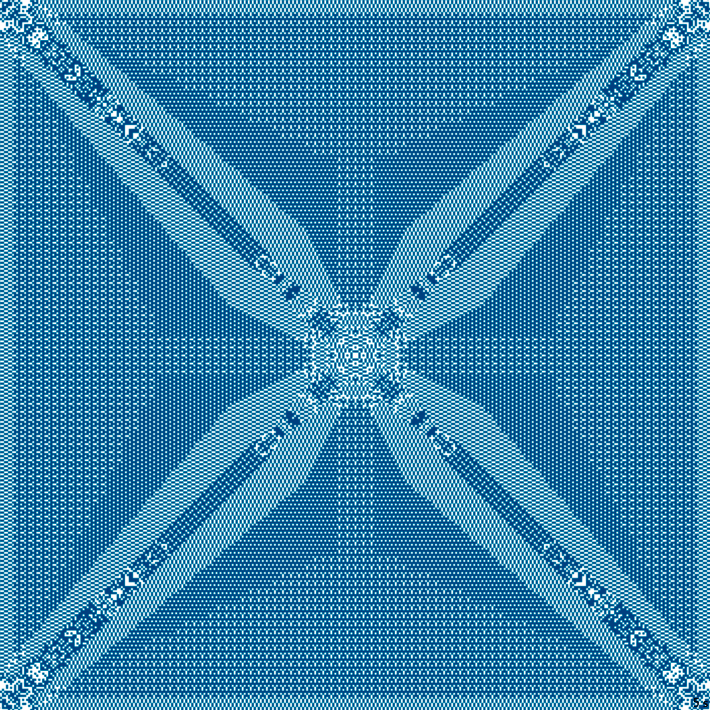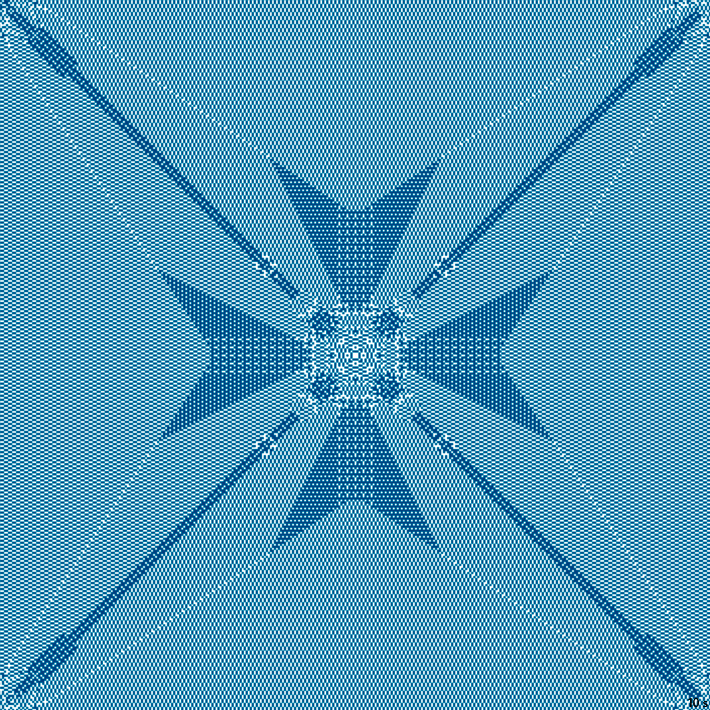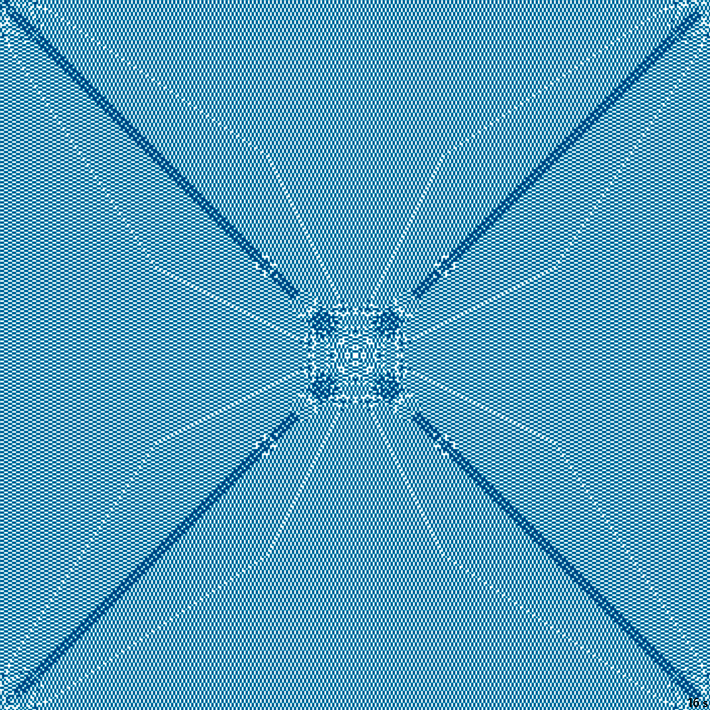
16с., 356×356, 1×100%; для сглаживания мерцания обрезан каждый второй фрейм
❯ Пользовательские шаблоны окрестностей
Хоть через ручную нотацию и можно реализовать любую другую окрестность (кроме взвешенных, у них собственный аналог), она не является полноценной заменой. Ручная окрестность неудобна, сложно воспринимается, и, что главное, – она строго ограничена тем радиусом, под который написана. Шаблоны окрестностей лишены этих недостатков. Мы уже рассматривали 10 «признанных» окрестностей, но, так как потенциал для создания новых шаблонов огромен, пользователи не преминули описать собственные.
Конечно, пытаться упомянуть все наработки нет ни возможности, ни смысла, потому мы, для примера, рассмотрим только набор шаблонов предложенных энтузиастом Antonio Sánchez Chinchón, которые он описал при реализации собственного симулятора циклических КА.
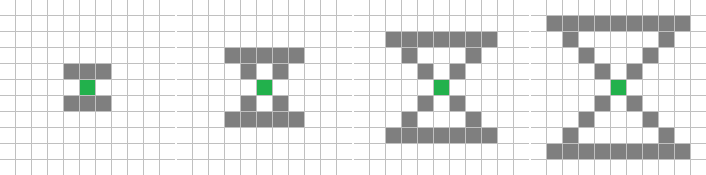
Контур Мура

Вид окрестности на радиусах 1-4
Первый шаблон в этом списке просто убирает внутренние клетки у самой базовой окрестности. Мы уже упоминали этот и два следующих предложенных шаблона в материале о циклических КА, а сейчас взглянем на примеры в HROT-конфигурации.
Правило:
(abs(x) == R) | (abs(y) == R)Обозначение: Mr
Обозначение в нотации исключительно авторское и, к сожалению, не поддерживается популярными симуляторами, впрочем, как и пользовательские шаблоны в целом. Они могут быть реализованы только в таких же пользовательских симуляторах, а для использования в, например, Golly и LifeViewer придётся делать переложения на N@/NW под каждый радиус.

61с., 356×356, 50×70%| R3/G3/S9-20/B4,7/NMr

13с., 356×356, 1×100%| R3/G3/S2-6,8,10,12,14,16,18,20,22,24/B1-2,4,6/NMr
Контур фон Неймана

Аналогично предыдущему модифицируется и вторая по популярности окрестность. На чётных радиусах мы можем наблюдать разделение поля на две части, в зависимости от чётности.
Правило:
abs(x) + abs(y) == RОбозначение: Nr

24с., 237×237, 6×100%| R4/G2/S5-16/B5,13-16/NNr
Поведение чётных/нечётных полей можно дополнить нечётной циклической сеткой – так, переходя по связанным границам, фигура будет менять чётность.

28с., 237×237, 100×15%| R4/G3/S4-11/B6-9/NNr
S-shape #1
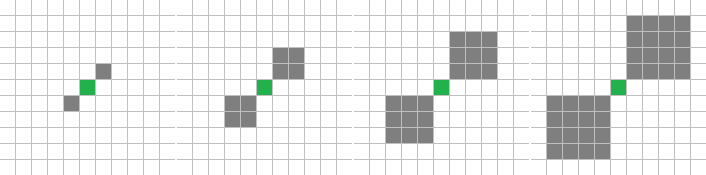
Первый пример направленного шаблона.
Правило:
((y < 0) & (x > 0)) | ((y > 0) & (x < 0))Обозначение: S1
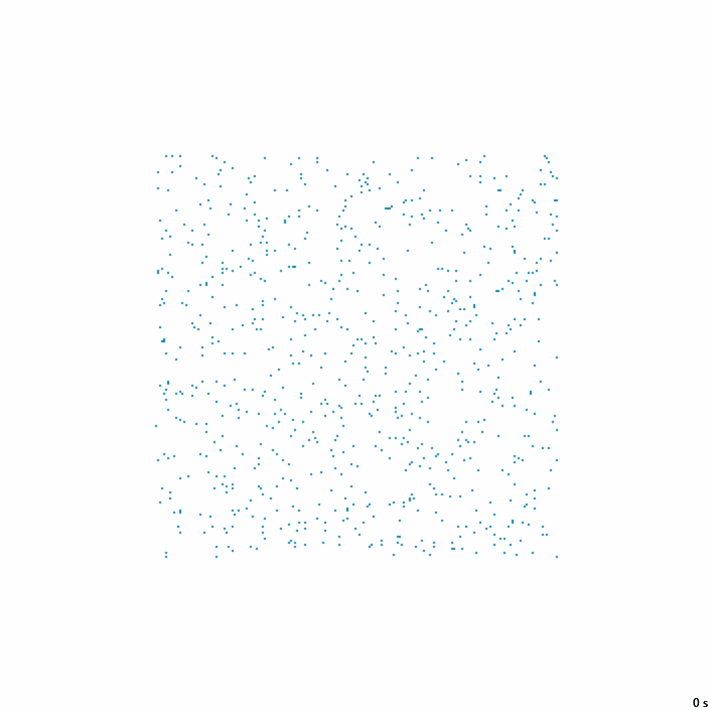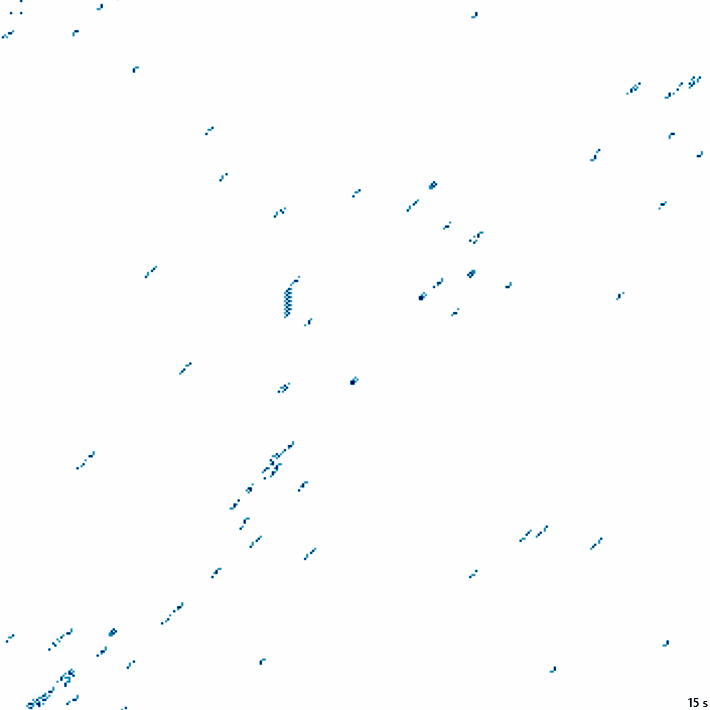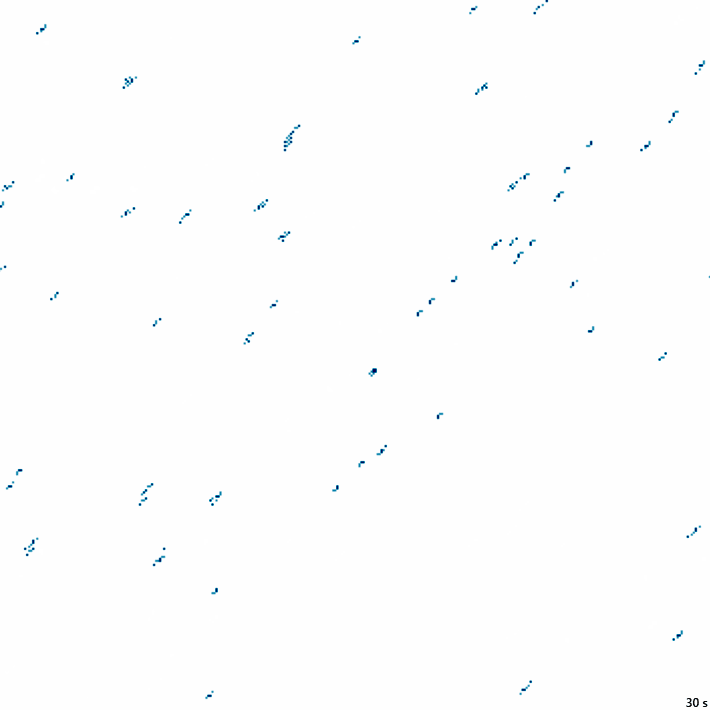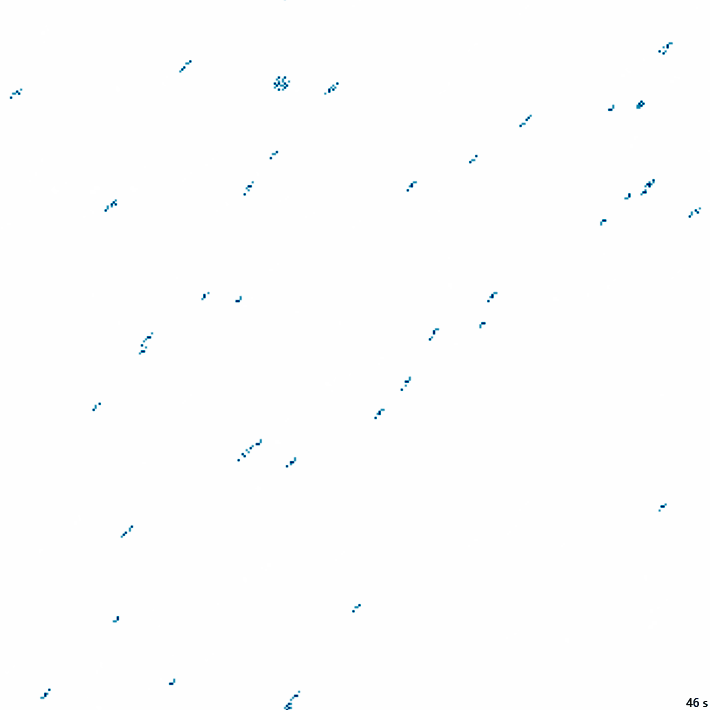
48с., 356×356, 200×2% | R2/G3/S5/B2/NS1

8с., 356×356, 2×100% | R7/G4/S0-7/B1-2/NS1
Hourglass

Правило:
abs(y) > abs(x)Обозначение: D1

31с., 712×712, 200×100% | R3/G2/S3-16/B7-9/ND1

43с., 356×356, 200×10% | R3/G4/S3/B4-6/ND1
Hourglass remote
Правило:
(abs(y) == abs(x)) | (abs(y) == R)Обозначение: D2

15с., 356×356, 200×20% | R4/G2/S2-5/B4/ND2

10с., 178×178, 20×100% | R2/G2/S1-9/B3/ND2
Углы

Или же «инвертированная окрестность фон Неймана».
Правило:
abs(y) + abs(x) > RОбозначение: C2

14с., 356×356, 8×100% | R4/G4/S1-9/B8-40/NC2
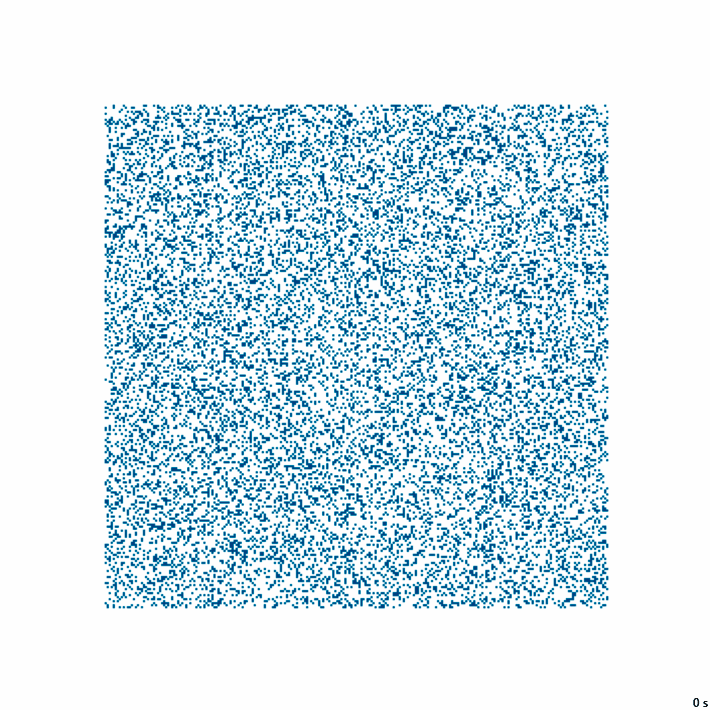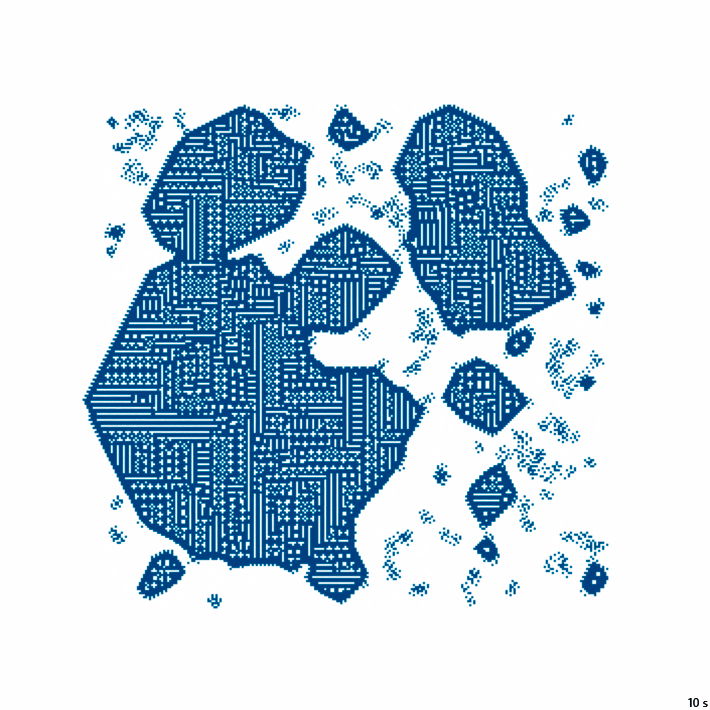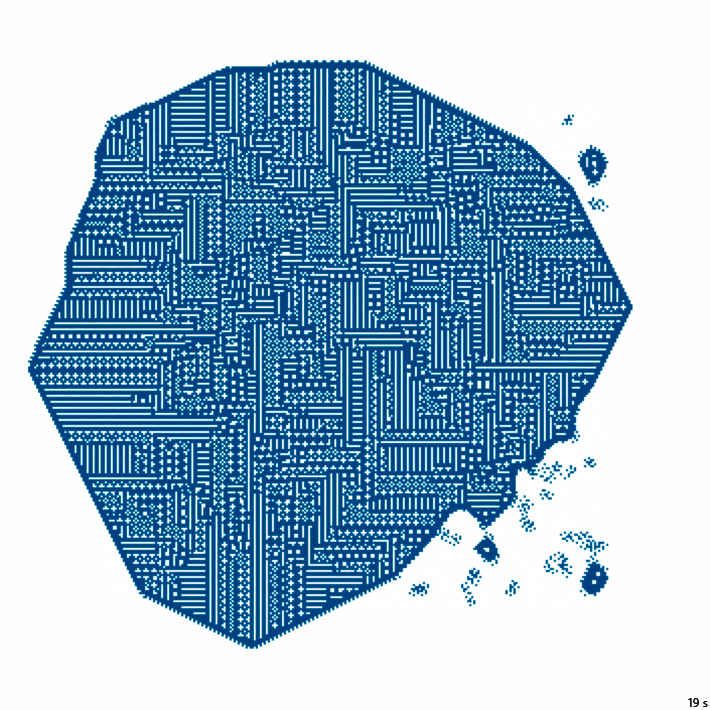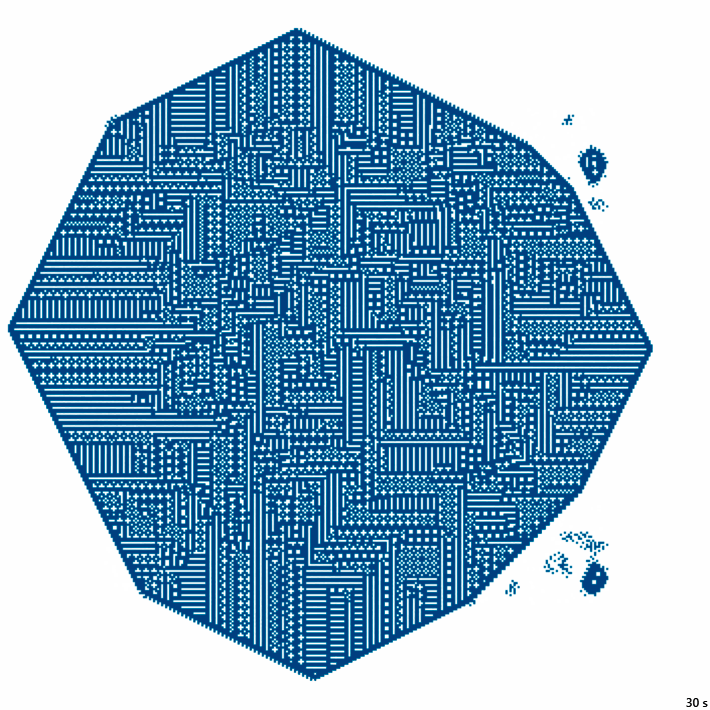
30с., 356×356, 250×25% | R2/G2/S3-11/B6-9/NC2
Tick Mark

Комбинация диагонального креста и контура Мура.
Правило:
(abs(y) == abs(x)) | (abs(y) == R) | (abs(x) == R)Обозначение: TM
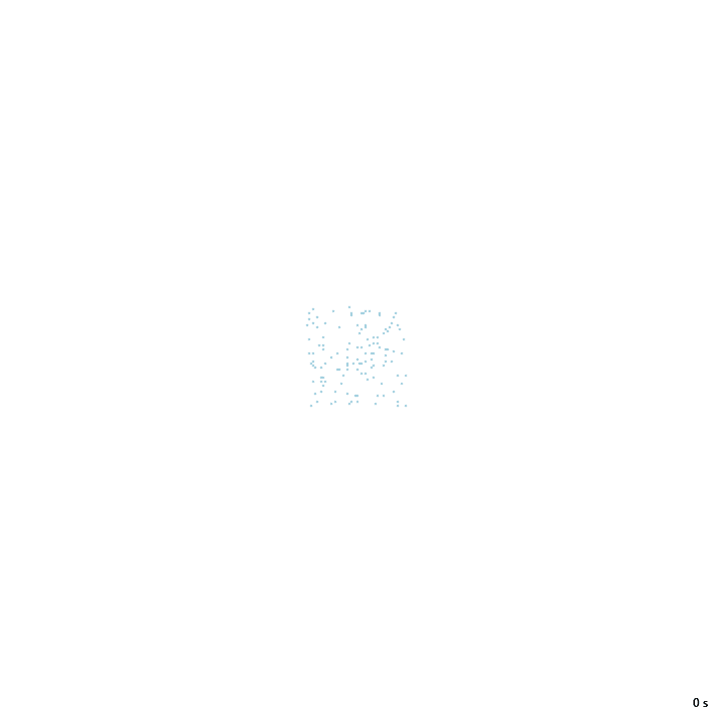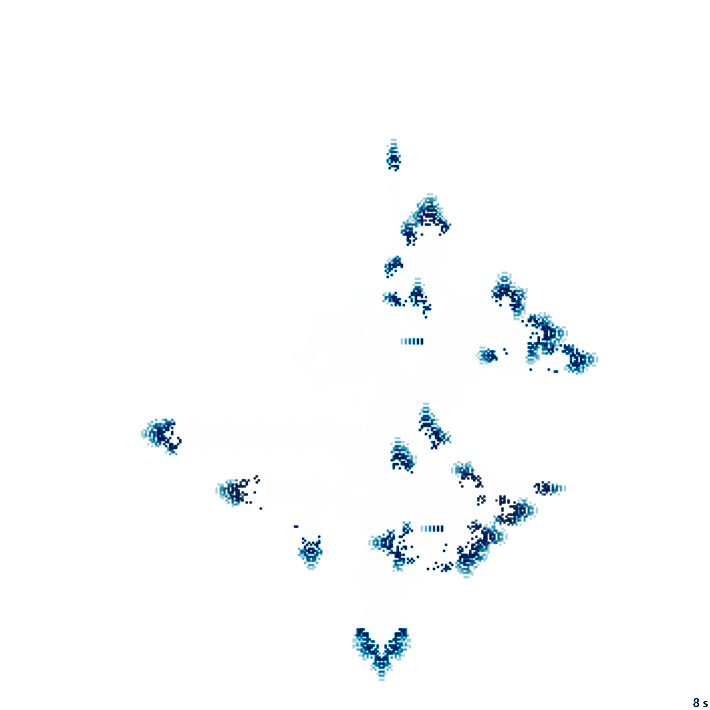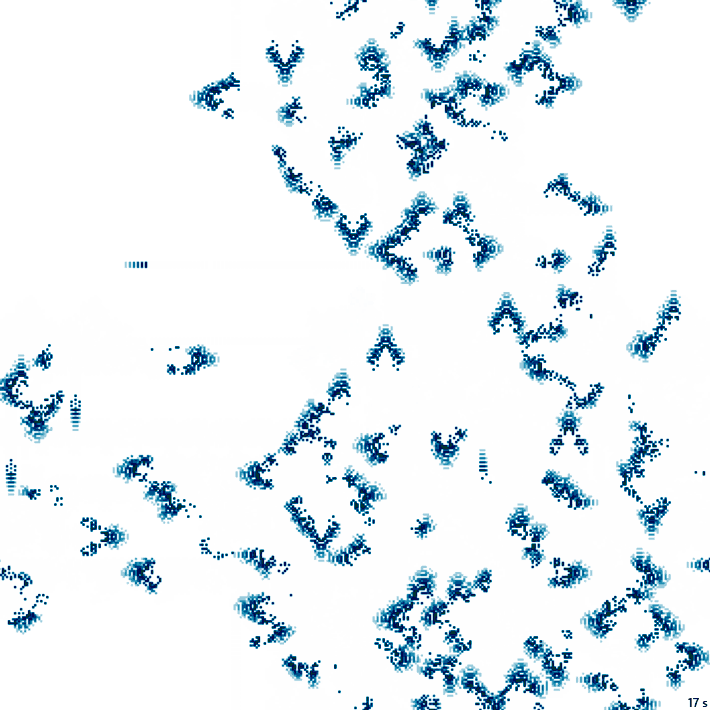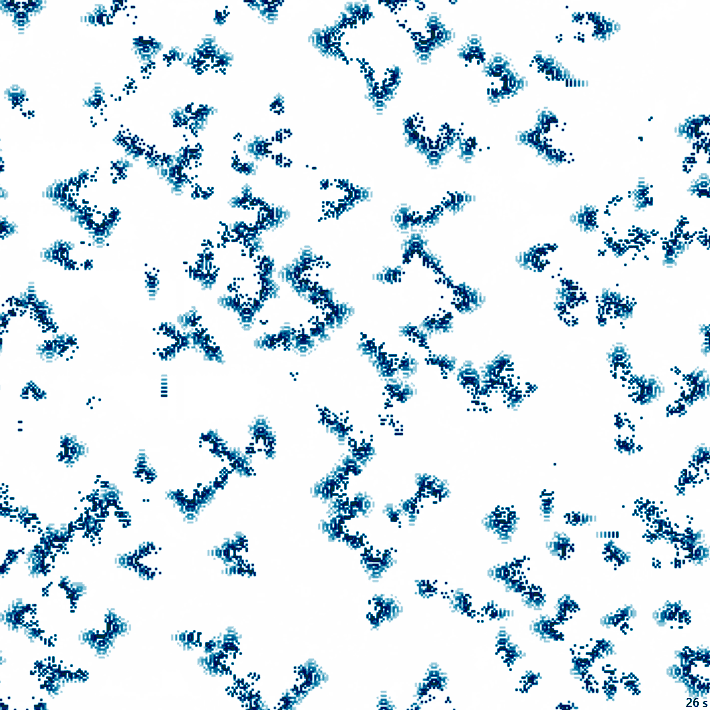
26с., 356×356, 50×5% | R2/G7/S6-15/B3/NTM
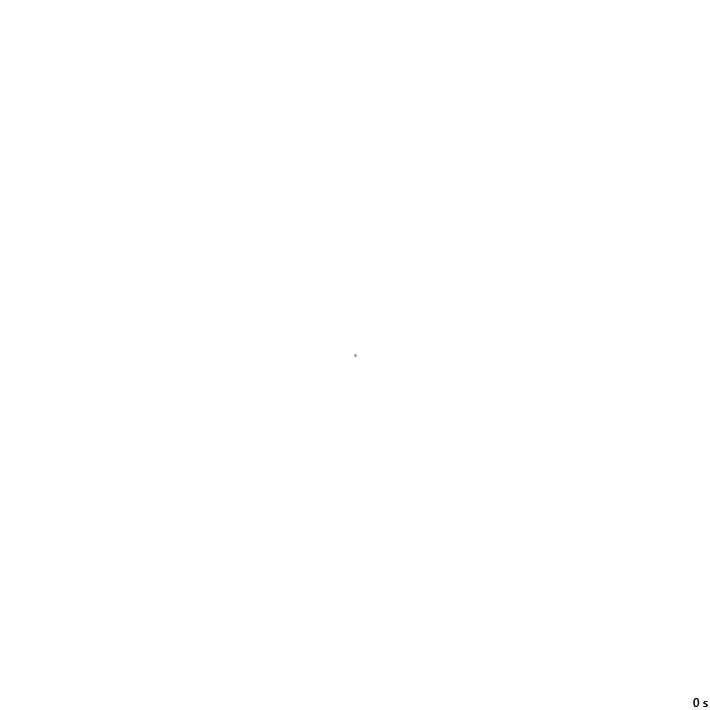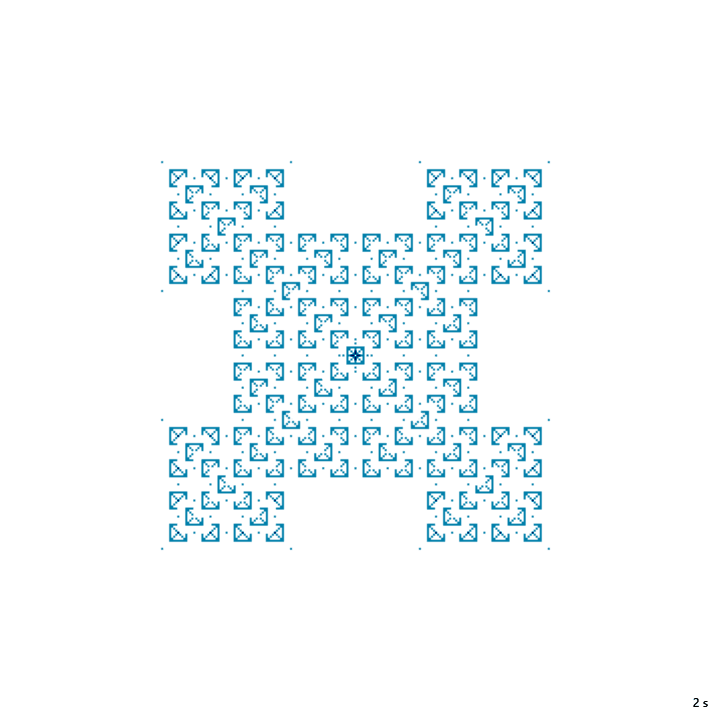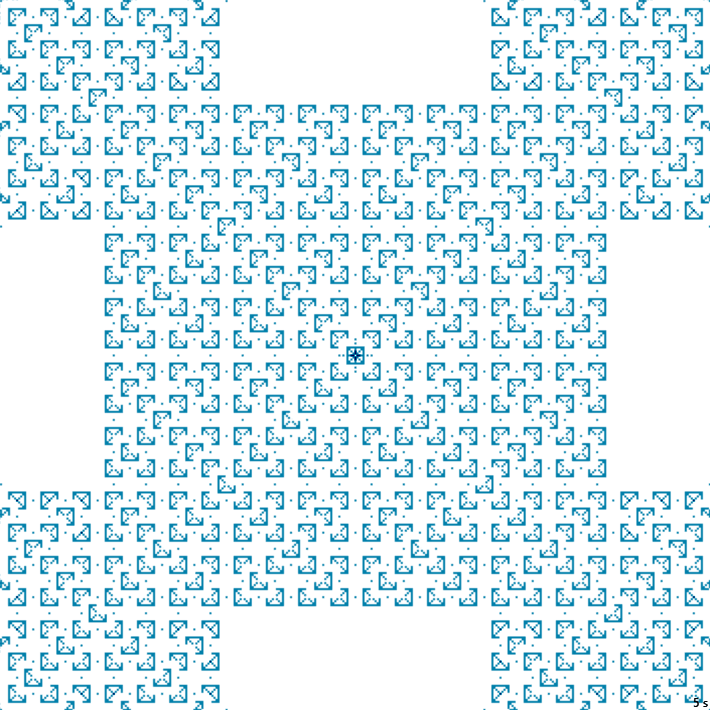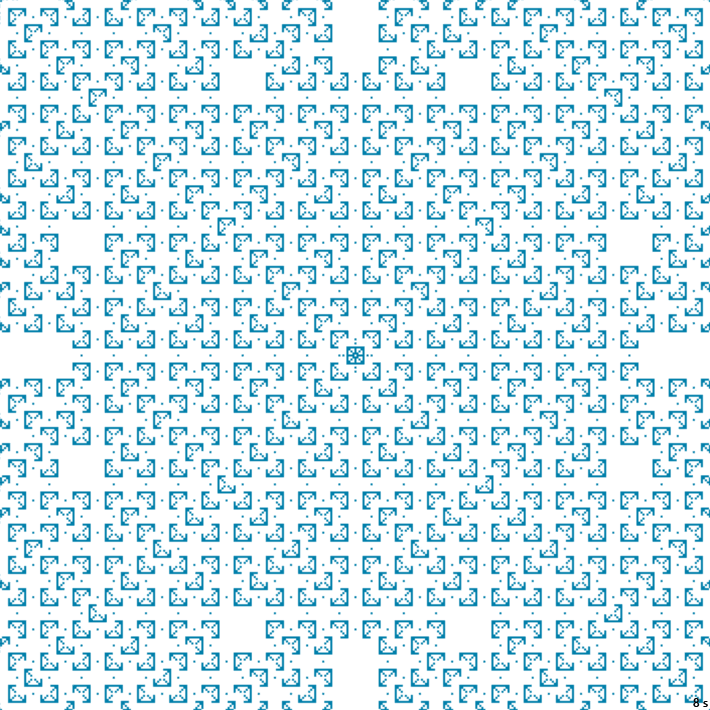
8с., 356×356, 1×100% | R4/G3/S0-20/B1,17-30/NTM
S-shape #2

Правило:
(x == 0) | (y == R) & (x < 0) | (y = -R) & (x > 0)Обозначение: S2

23с., 356×356, 50×20% | R4/G2/S/B3/NS2

20с., 712×712, 2×100% | R2/G2/S1-5/B1/NS2
Бонус: больше окрестностей
Буквально по одному случайному примеру на окрестность.
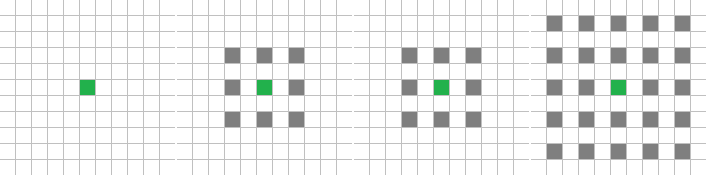
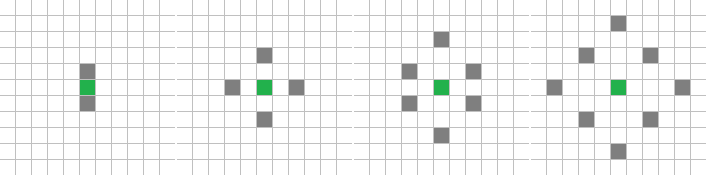
Шахматная доска mod 2 – Nb3 –
8с., 356×356, 1×100% | R4/G2/S0-9/B1/Nb3
Контур фон Неймана mod 2 – Nrl –

40с., 356×356, 50×95% | R4/G3/S/B2/NNrl

T – NT –

H – NH2 –

52с., 356×356, 50×15% | R3/G2/S1-2/B4/NH2

М – NM2 –

15с., 356×356, 1×100% | R2/G2/S0-2,4/B1/NM2
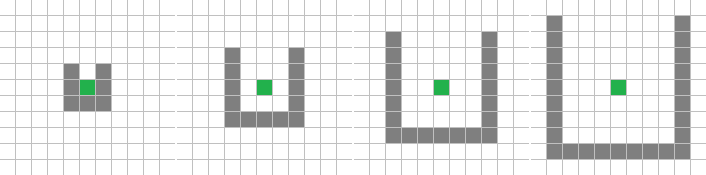
U – NU –

34с., 356×356, 50×15% | R3/G3/S/B4-5/NU

Z – NZ –
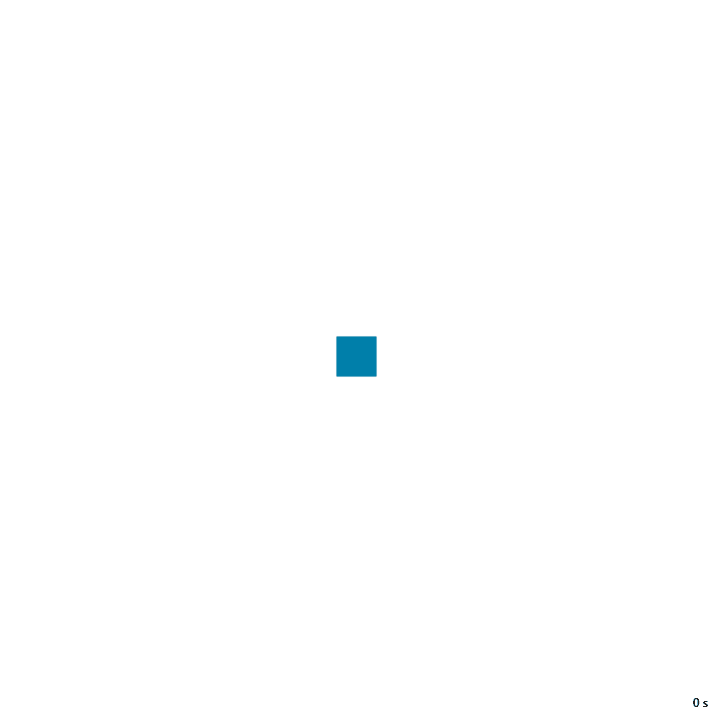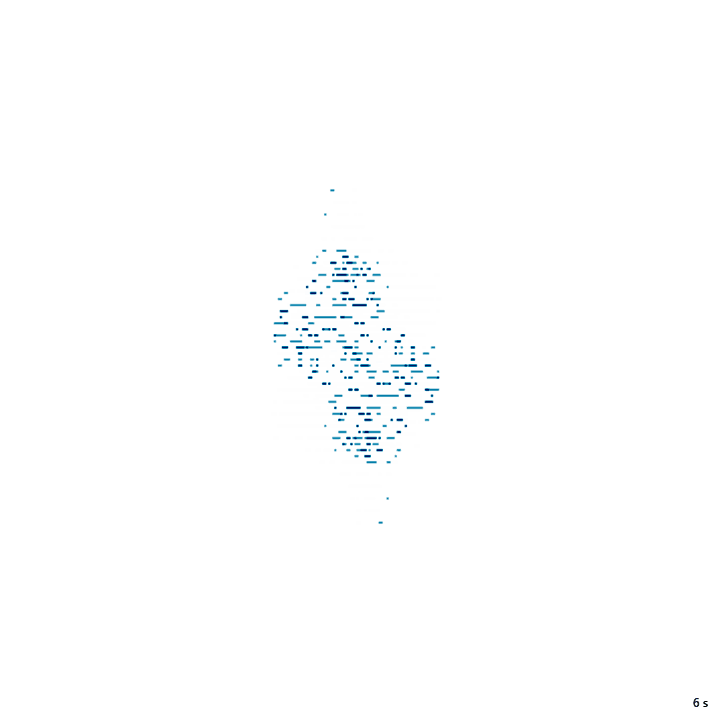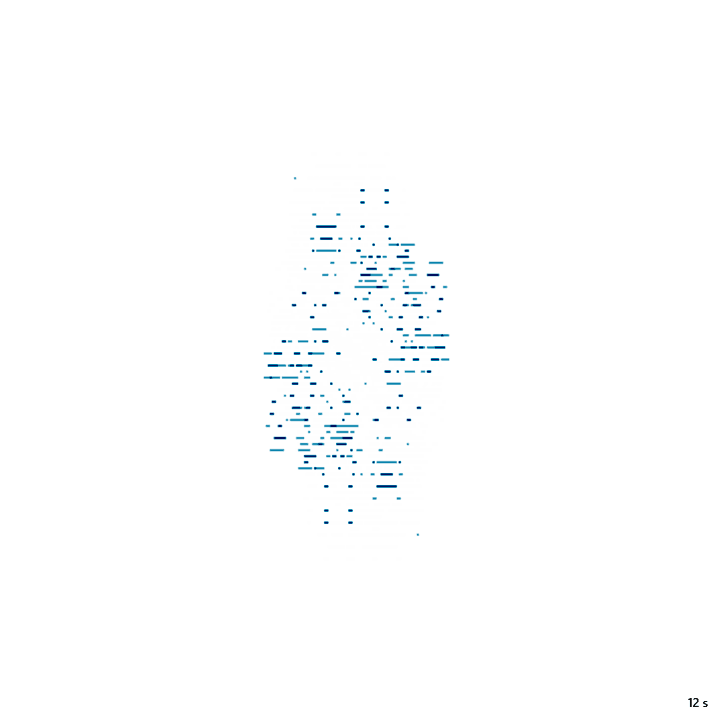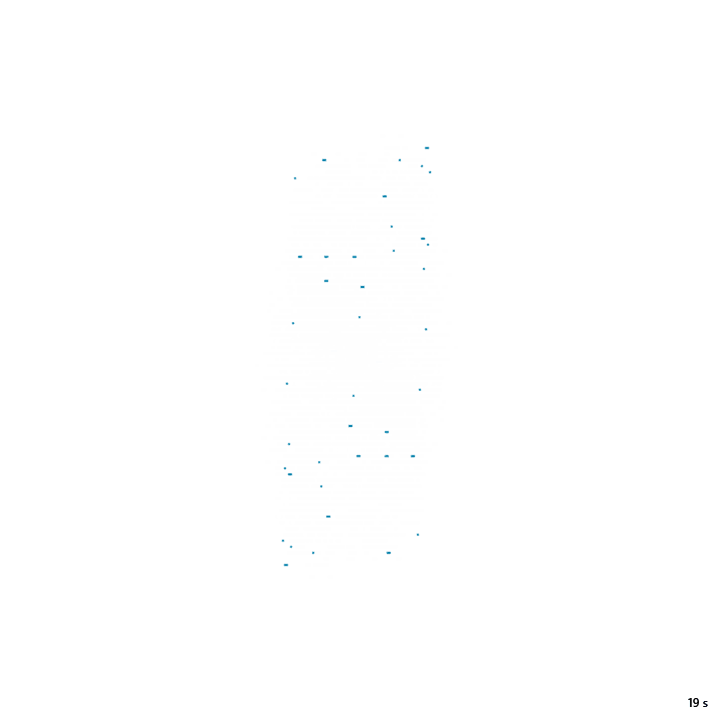
19с., 356×356, 20×100% | R6/G3/S0/B5-6/NZ
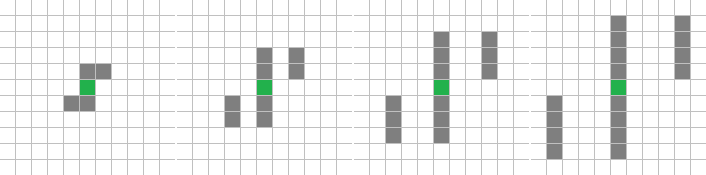
Линии – Nln –

27с., 356×356, 50×20% | R3/G2/S1/B3/Nln

Шахматная доска mod 2 – Nb3 –
(x % 2 == 0) & (y % 2 == 0)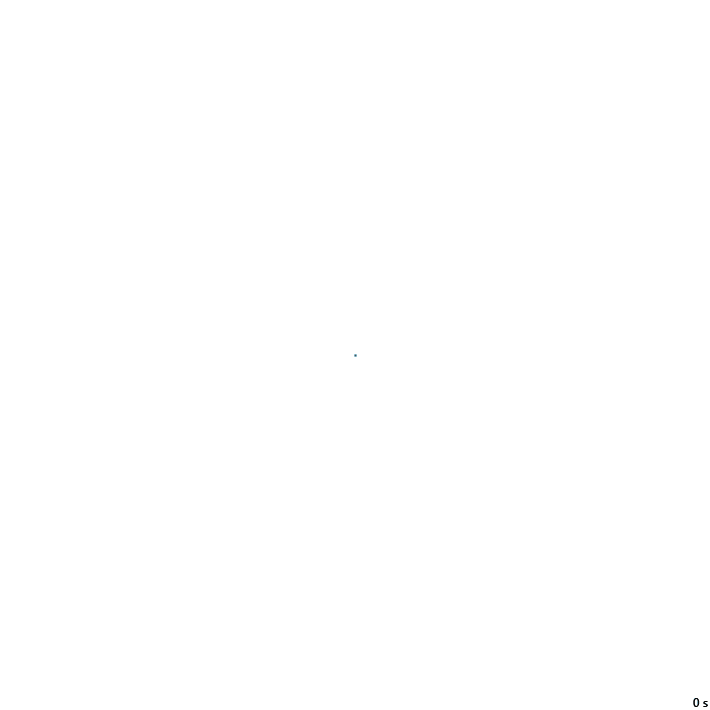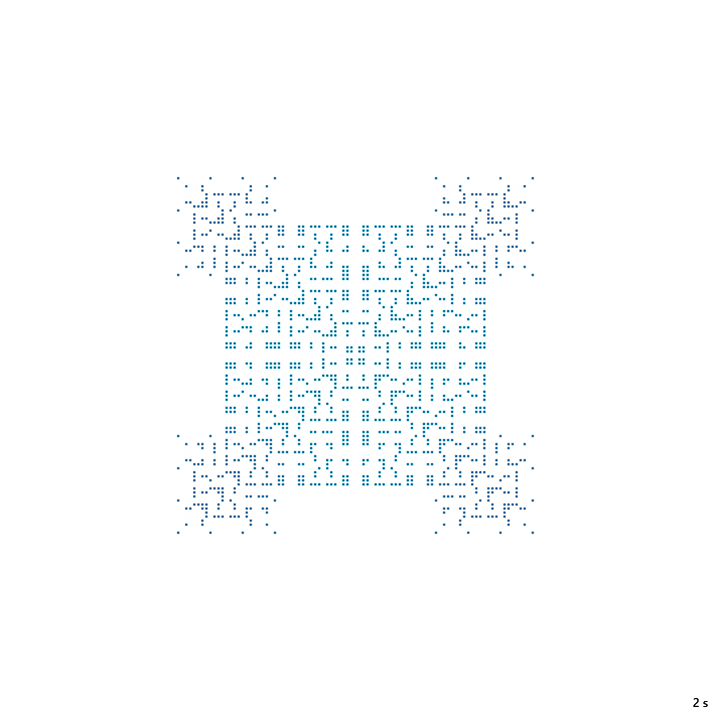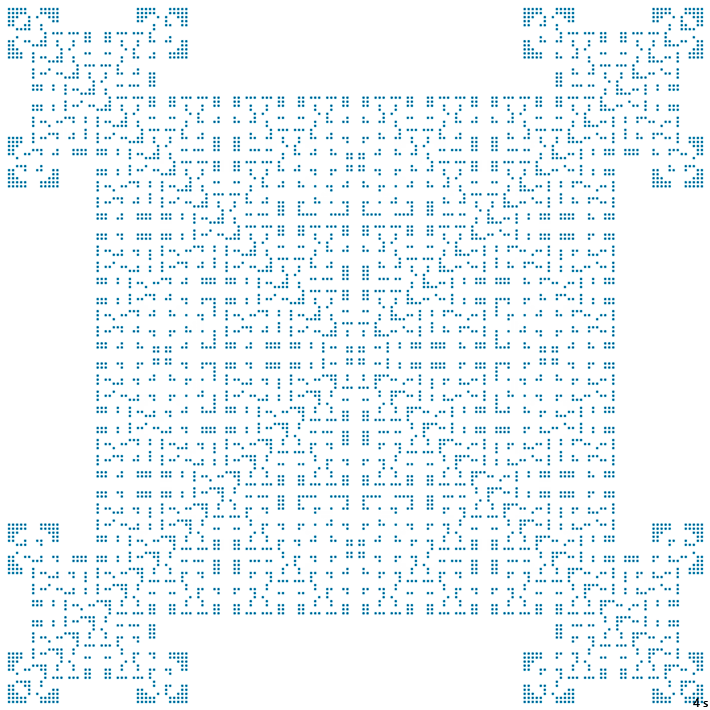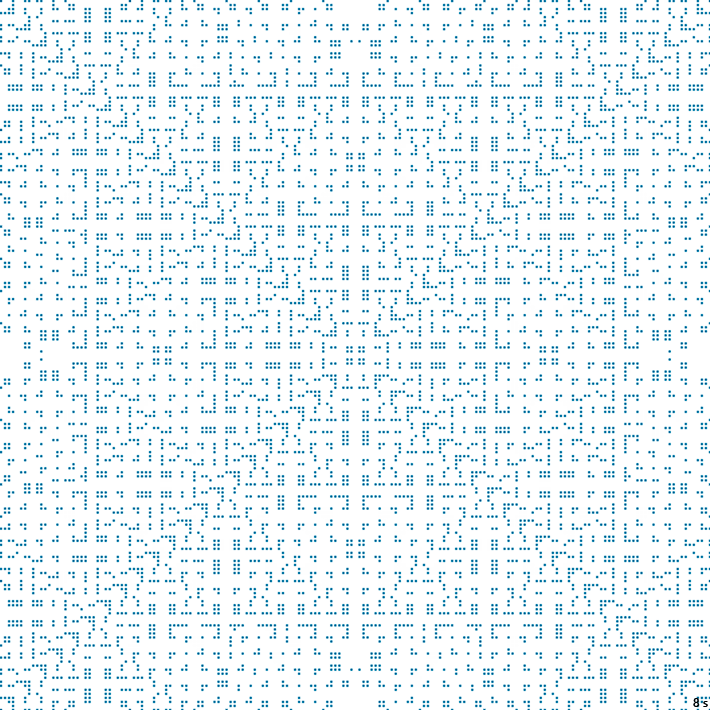
8с., 356×356, 1×100% | R4/G2/S0-9/B1/Nb3

Контур фон Неймана mod 2 – Nrl –
(abs(y) + abs(x) == R) & (x % 2 == 0)
40с., 356×356, 50×95% | R4/G3/S/B2/NNrl
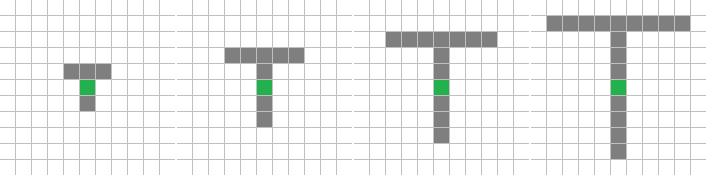
T – NT –
(x == 0) | (y == -R)
Мерцание и немного залипание. Осторожно.

41с., 356×356, 10×100% | R3/G2/S0-5/B2-3/NT

41с., 356×356, 10×100% | R3/G2/S0-5/B2-3/NT

H – NH2 –
(y == 0) | (abs(x) == R)
52с., 356×356, 50×15% | R3/G2/S1-2/B4/NH2

М – NM2 –
(abs(x) == R) | (abs(y) == abs(x)) & (y > 0)
15с., 356×356, 1×100% | R2/G2/S0-2,4/B1/NM2

U – NU –
(y == R) | (abs(x) == R)
34с., 356×356, 50×15% | R3/G3/S/B4-5/NU

Z – NZ –
(abs(y) == R) | (y == -x)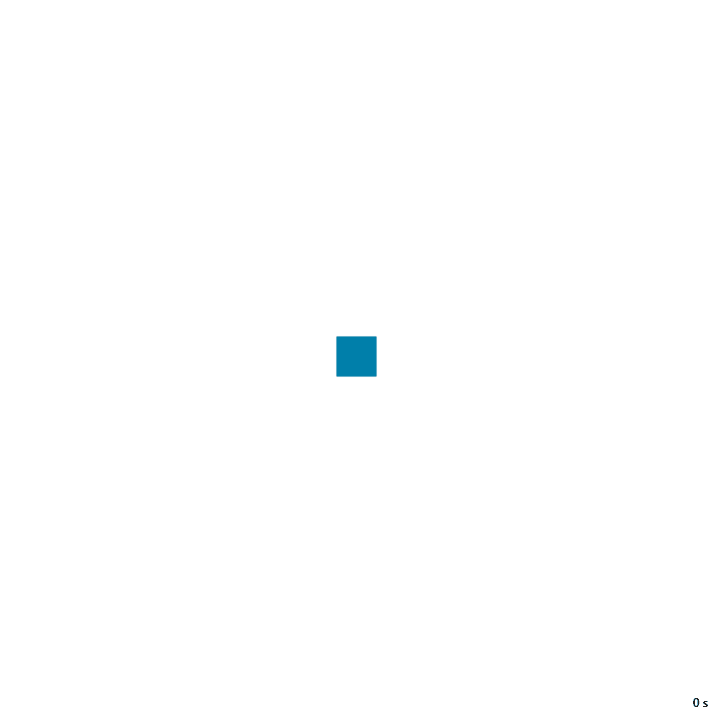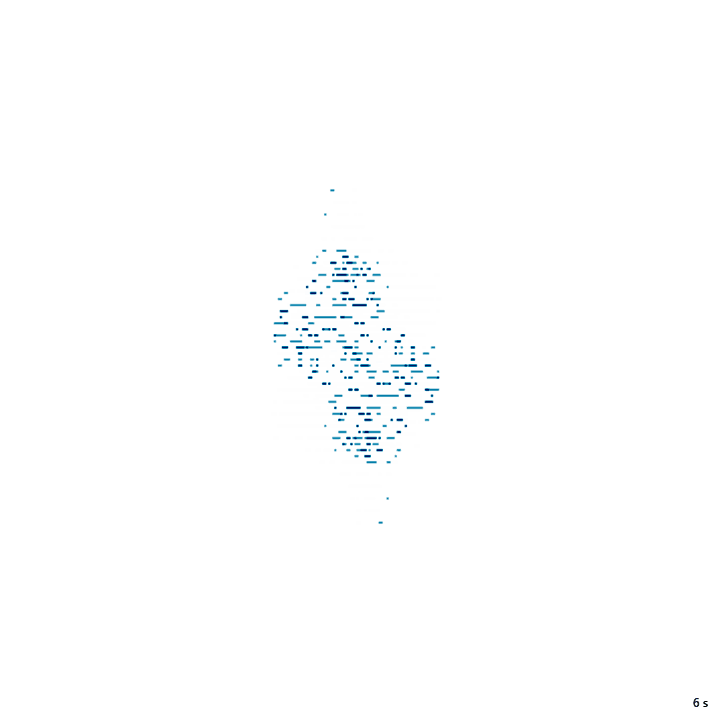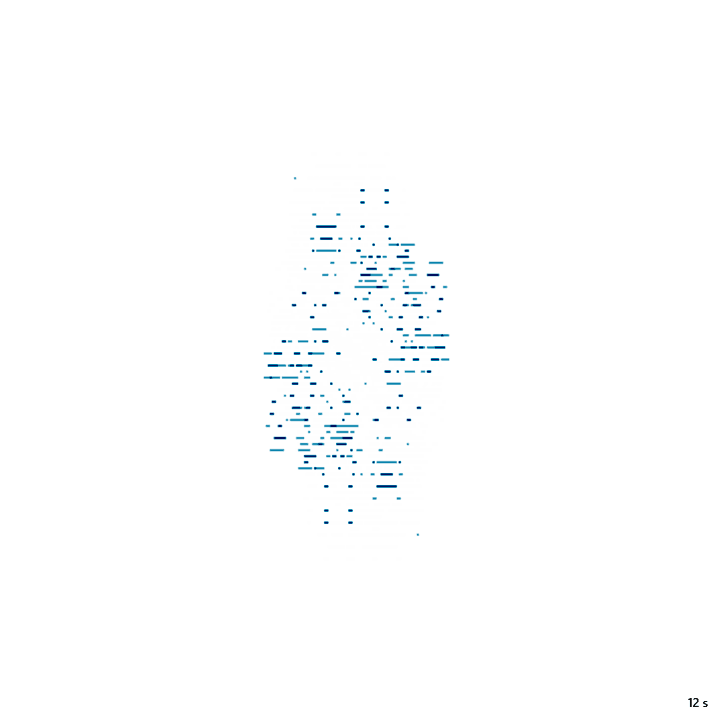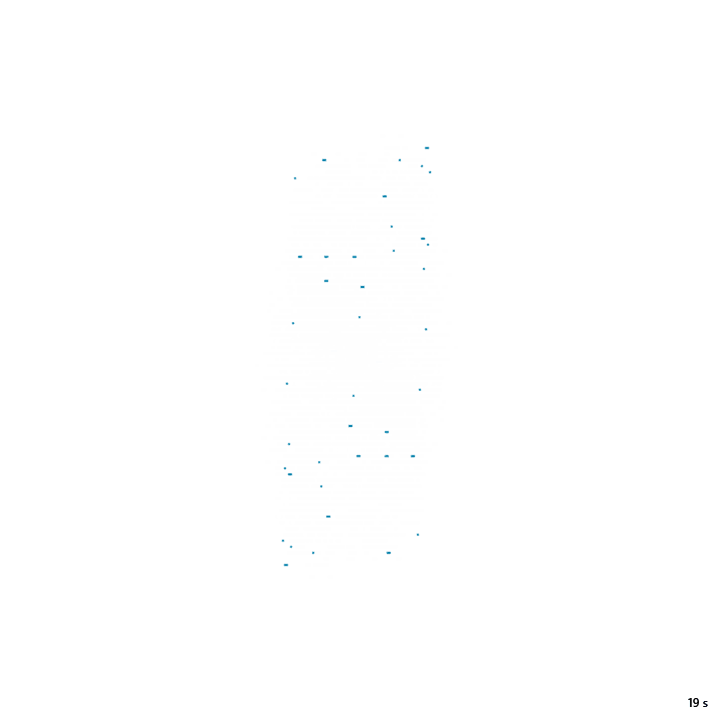
19с., 356×356, 20×100% | R6/G3/S0/B5-6/NZ

Линии – Nln –
(x == 0) | (x == R) & (y < 0) | (x == -R) & (y > 0)
27с., 356×356, 50×20% | R3/G2/S1/B3/Nln
Читайте также
О клеточных автоматах:
Прочее:
- Базовая «life-like» конфигурация
- Старение клеток: параметр поколений
- Нотация Хенселя: учёт расположения соседей
- LtL: расширенный радиус поиска соседей
- Циклические клеточные автоматы
- Альтернативные окрестности и HROT
- Блочные КА, окрестность Марголуса
- Взвешенные окрестности, окрестность Гаусса, Far Corners/Edges
- Направленные и пользовательские окрестности (вы здесь)
- Клетки-киллеры, BSFK[L]
- Дефицитные правила
- Обратные и расширенные поколения
- Моделирование лесных пожаров: теория, клеточный автомат на Python
- Сегрегация общества: модель Шеллинга и распределение этнических групп в городах Израиля
Прочее:
- 🟢 История моделирования лесных пожаров
- 🟠 REcollapse: фаззинг с использованием unicode-нормализации
- 🔵 Хватит использовать [a-zа-яё]: правильная работа с символами и категориями Unicode в регулярных выражениях
- 🟢 Краткая история календаря и фантазии о шестидневной неделе
- 🟢 Пройти LeetCode за год: экскурсия по сайту и roadmap
← Предыдущая часть | Следующая часть →
