В ноябре Nature опубликовал работу учёных Женевского университета (UNIGE) и канадского Университета Макгилла, которые решили заменить привычную систему PIN-кодов на более безопасную. В поисках сверхнадежной аутентификации исследователи предложили пересмотреть фактор владения и опираться на метод математического доказательства с нулевым разглашением в связке со специальной теорией относительности.
Нам стало любопытно, как это могло бы работать, и мы полезли внутрь научной работы – в надежде разглядеть там аутентификацию будущего.

Задача: сверхнадежный банкомат
Для иллюстрации гипотезы учёные взяли стандартную ситуацию, где мы постоянно используем PIN-коды, – снятие наличных в банкомате.
Как обычно выглядит ситуация: пользователь вставляет в банкомат карту, складывает руки домиком над клавиатурой, вводит секретный PIN-код и запрашивает нужную сумму.
Сама задача на абстрактном уровне выглядит так:
с одной стороны, у нас есть "доказывающий" – пользователь, который хочет подтвердить, что он это он, для совершения определенных действий;
с другой стороны – "проверяющий", который обрабатывает информацию от пользователя и сверяет ее.
Как комментируют учёные, процедура основана на допущении, что обе стороны доверяют друг другу. Пока у нас есть "честный доказывающий" и "честный проверяющий", все хорошо: транзакция совершается, данные никуда не утекают.
Но на практике доверие может быть обмануто с обеих сторон:
нечестный "доказывающий" и честный "проверяющий", например, когда мошенник украл чужую карту и PIN-код и пытается выдать себя за другого, чтобы получить деньги;
честный "доказывающий" и нечестный "проверяющий", например, если банкомат взломан мошенниками, которые при работе с ATM пытаются завладеть номером карты и PIN.
Эту систему можно усилить дополнительным фактором, например, одноразовым паролем (OTP). Но если мошеннику повезет, то и эту информацию удастся украсть. Допустим, он сможет установить камеру над банкоматом и заснять все действия пользователя с распечатанными одноразовыми кодами. Или взломает сервер, который генерирует одноразовые коды.
Поэтому в поисках более надежной системы учёные решили "отбросить все допущения" и изобрести что-то получше PIN и одноразовых кодов.
На первом этапе они обратились к доказательству с нулевым разглашением – принципу, довольно популярному в сфере криптовалют.
Как работает доказательство с нулевым разглашением
"Представьте, что я хочу продемонстрировать доказательство теоремы перед коллегами, – объясняет Николас Бруннер, профессор кафедры прикладной физики факультета естественных наук UNIGE. – Когда я покажу им этапы доказательства, они убедятся в его верности. Но вместе с тем они получат доступ ко всей информации и смогут легко воспроизвести доказательство". Если мы не доверяем коллегам и хотим предотвратить возможное восстановление доказательства, нам нужен способ показать свою осведомленность без разглашения самой информации. Это по своей сути и будет доказательством с нулевым разглашением.
Принцип был изобретен в середине 1980-х годов и сейчас активно применяется на практике в криптографии. Его использование в процессе аутентификации можно сравнить с игрой-головоломкой.
Предположим, у нас есть друг Джон, который видит мир черно-белым. При этом мы сами видим мир цветным. Наша цель – доказать Джону, что мы действительно можем видеть цвета. Но при этом мы не должны называть цвета, так как не можем полностью доверять Джону.
Чтобы проверить нас, Джон показывает нам красную и синюю карточку. Затем он убирает их за спину и либо меняет местами, либо оставляет все как есть. После Джон снова раскладывает карточки перед нами и спрашивает: "Я поменял их?" Даже если повторить игру сто раз, у нас всегда будет правильный ответ, потому что мы можем видеть цвета. Так что после длинной цепочки правильных ответов Джон в конце концов скажет: "Хорошо, я тебе верю. Ты можешь видеть цвет".
У женевских и канадских учёных в качестве "игры с карточками" используется известная математическая задача.
"Мы обратились к проблеме трехцветной раскраски. В одном из вариантов этой задачи используются графы: набор узлов, часть из которых соединены ребрами, а часть не соединены", – объясняет Хьюго Збинден, профессор кафедры прикладной физики в UNIGE. Каждому узлу графа присваивается один из трех возможных цветов – желтый, синий или красный.
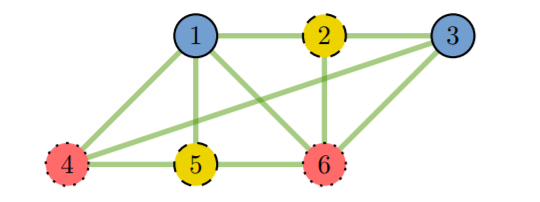
При этом два узла, связанные ребрами, всегда должны быть разных цветов. Так что если сделать граф достаточно большим, то подбор раскраски для него может стать серьезной математической задачей. Знание правильной раскраски такого графа и будет нашим доказательством.
Если перенести эту задачу на банкоматы:
Каждому пользователю мы предоставляем токен с уникальным графом и уже запрограммированным решением для трехцветной раскраски. Раскраска графа регулярно меняется в соответствии с заданным алгоритмом: что было желтым, становится синим, синий становится красным и т. д.
Пользователь подключает устройство к внешнему разъему банкомата.
Банкомат проверяет токен: отправляет сотни тысяч запросов и уточняет цвет отдельных элементов графа. На практике такую проверку экспериментаторы выполняют более трех миллионов раз менее чем за три секунды.
Поскольку у пользователя на токене есть готовое решение для раскраски, то он всегда быстро и верно отвечает на запросы и подтверждает знание трехцветной раскраски своего графа.
При этом в процессе аутентификации банкомат не получает полную раскраску всего графа, а только убеждается в непротиворечивости его раскраски.
В чем здесь усовершенствование по сравнению с распространенной схемой TOTP? В старой схеме, когда мы генерируем одноразовые коды с привязкой ко времени, у нас чаще всего есть устройство с приложением для генерации кодов. Сами коды генерируются на стороне проверяющего сервера: раз в n секунд последовательность символов меняется. Сервер и личное устройство синхронизированы между собой по времени. Но теоретически здесь возможны атаки MITM. Скажем, мы можем взломать алгоритм, который генерирует последовательность символов, предсказать следующий код и воспользоваться им.
В новом алгоритме от UNIGE есть 2 важных улучшения: сложность алгоритма и его носитель. Во-первых, даже если часть ответов токена утечет к злоумышленникам, хакерам будет трудно восстановить полную раскраску для большого графа. За основу исследователи взяли трехцветную вершинную раскраску графа с 5000 узлов и 10 000 ребер. Чтобы решить такую задачу, нужны огромные вычислительные мощности. Раскрасить граф с помощью простого перебора вариантов вряд ли получится быстро. Во-вторых, мы исключаем возможность взлома на стороне "проверяющего". Сам банкомат обладает только механизмом проверки контрольных значений и не содержит информации о раскраске пользовательского графа. То есть минус один источник утечки информации.
Звучит уже убедительно. Тем не менее, такой уровень безопасности системы не вполне устраивал команду исследователей в долгосрочной перспективе.
"Функции кодирования, которые вычисляются в одном направлении, зачастую сложно декодировать, то есть вычислить в обратном направлении. Но это не невозможно", – комментирует Себастьен Дизаньоль, физик из Женевского университета и соавтор исследования. Например, если вы умножаете простые числа и получаете очень большое число, вернуться к исходным числам трудно. Но при должной настойчивости и достаточных вычислительных мощностях это можно сделать. Особо привлекательные для хакеров цели могут подвергаться изнурительным направленным атакам, для которых все средства хороши.
В связи с этим учёные выдвигают новую гипотезу: а что насчет второго устройства и второго токена в качестве дополнительного фактора аутентификации?
"В этом случае реализация похожа на способ допроса у полицейских. В процессе расследования детективы допрашивают двух подозреваемых одновременно в разных комнатах, чтобы они не могли общаться во время дачи показаний, – говорит Дизаньоль. – Если подозреваемые рассказывают одну и ту же версию истории, то высока вероятность, что они говорят правду".
И это как раз тот момент, когда на сцене появляется Эйнштейн.
При чем здесь релятивистские принципы
Итак, при использовании сразу двух устройств мы разделяем проверку на две пары доказывающий-проверяющий. На практике это означает, что мы подключаем сразу два отдельных токена с уникальными графами к двум отдельным банкоматам. Банкоматы одновременно отправляют запросы насчет трехцветной раскраски графов.
В этом случае хакеру для перехвата учетной записи потребуется сбрутить не один, а два больших графа за одно и то же время. То есть происходит линейное усложнение задачи. Но почему, по мнению учёных, решение становится невозможным?
Чтобы удостовериться в невозможности общения устройств друг с другом, учёные предлагают опираться на специальную теорию относительности. В основе доказательства безопасности лежит постулат, что мы не можем двигаться быстрее скорости света. Это распространяется и на скорость передачи данных.
"Со специальной теорией относительности, – продолжает Дизаньоль, – кажется вполне разумным верить, что условие безопасности – не вычислительное, а физическое ограничение... поскольку информация не может распространяться быстрее скорости света".
Другими словами, исследователи пытаются предложить хакерам задачу за гранью физики. По задумке учёных, пока два банкомата будут отправлять запросы токенам достаточно быстро, задержки между вопросом и ответом токена всегда будут меньше, чем время для передачи информации на расстоянии. В каком-то смысле токены не успеют обсудить свое "алиби" между собой, чтобы подделать проверку.
В эксперименте учёные проверили работу такой системы на расстоянии 390 м и 60 м между банкоматами. В будущем они планируют снизить расстояние до метра.

Казалось бы, задача решена. Но у исследователей остается последний вопрос. Эти релятивистские ограничения не столь бесспорны, когда речь заходит о нетрадиционной физике. И тут добро пожаловать в квантовые вычисления.
А что насчет "квантовых хакеров"?
Квантовая механика допускает принцип, называемый квантовой запутанностью. Проще говоря, когда две квантовые частицы, а именно частицы света, запутаны, они могут мгновенно взаимодействовать.
"Предположим, у меня нет раскраски графа, но я хочу притвориться, что у меня она есть, – рассуждает Дизаньоль о действиях потенциального хакера. – Я мог бы придумать процедуру, использующую квантовую запутанность между двумя токенами, чтобы правильно ответить на вопросы. В некотором смысле я могу жульничать".
В настоящее время учёные размышляют, может ли сам протокол безопасности использовать квантовые доказательства вместо стандартных устройств.
Но пока это все теории. Даже если не заходить так далеко – насколько реально воплотить сверхзащищенные банкоматы? Посмотрим на практическую реализацию релятивистского доказательства.
Как релятивистское доказательство с нулевым разглашением реализовали на практике
В ходе эксперимента учёным было важно в первую очередь обеспечить максимально быстрое взаимодействие "доказывающего" и "проверяющего" без задержек.
Для этого в работе учёных использовались программируемые пользователем вентильные матрицы (ППВМ, или FPGA): плата Xilinx SP605 вместе со Spartan-6 XC6SLX45T. На их основе был реализован токен для пользователя и считывающее устройство для "банкомата". При этом на стороне банкомата также был установлен отдельный компьютер с процессором Intel core i3 и оперативной памятью в 4 ГБ для мониторинга и проверки консистентности ответов.
Для синхронизации времени между "проверяющими" была нужна связность между банкоматами. В эксперименте на 390 м учёные организовали синхронизацию "проверяющих" по GPS. На 60 м связь была организована по оптике с помощью многогигабитных трансиверов.

Прямо сейчас, говорит Дизаньоль, главной практической проблемой остается стоимость реализации. Для создания таких систем нужны чрезвычайно мощные чипы, и, скорее всего, очень дорогие.
Одна из гипотез состоит в том, чтобы использовать новые системы для крупных компаний, которые владеют защищенной информацией и могут позволить себе дорогие устройства и токены.
Так что, возможно, в ближайшем будущем такие схемы ждут нас именно на площадках с повышенным уровнем безопасности: в банках, дата-центрах, на объектах критической инфраструктуры.
Если хочется погрузиться в эксперимент глубже – вот первоисточники исследований и интервью авторов: