Всем давно известно, что на видеокартах можно не только в игрушки играть, но и выполнять вещи, никак не связанные с играми, например, нейронную сеть обучить, криптовалюту помайнить или же научные расчеты выполнить. Как так получилось, можно прочитать тут, а я хотел затронуть тему того, почему GPU может быть вообще интересен рядовому программисту (не связанному с GameDev), как подступиться к разработке на GPU, не тратя на это много времени, принять решение, нужно ли вообще в эту сторону смотреть, и «прикинуть на пальцах», какой профит можно получить.

Статья написана по мотивам моего выступления на HighLoad++. В ней рассматриваются в основном технологии, предлагаемые компанией NVIDIA. У меня нет цели рекламировать какие-либо продукты, я лишь привожу их в качестве примера, и наверняка что-то похожее можно найти у конкурирующих производителей.
Два процессора можно сравнить по разным критериям, наверное, самые популярные — это частота и количество ядер, размер кэшей и прочее, но в конечном счете, нас интересует, сколько операций процессор может выполнить за единицу времени, что это за операции вопрос отдельный, но наиболее распространенной метрикой является количество операций с плавающей запятой в секунду — flops. И когда мы хотим сравнить теплое с мягким, а в нашем случае GPU с CPU, эта метрика приходится как нельзя кстати.
Ниже на графике изображены рост этих самых флопсов с течением времени для процессоров и для видеокарт.

(Данные собраны из открытых источников, нет данных за 2019-20 годы, т.к. там не все так красиво, но GPU все-таки выигрывают)
Что ж, заманчиво, не правда ли? Перекладываем все вычисления с CPU на GPU и получаем в восемь раз лучшую производительность!
Но, конечно же, не все так просто. Нельзя просто так взять и переложить все на GPU, о том почему, мы поговорим дальше.
Привожу многим знакомую картинку с архитектурой CPU и основными элементами:
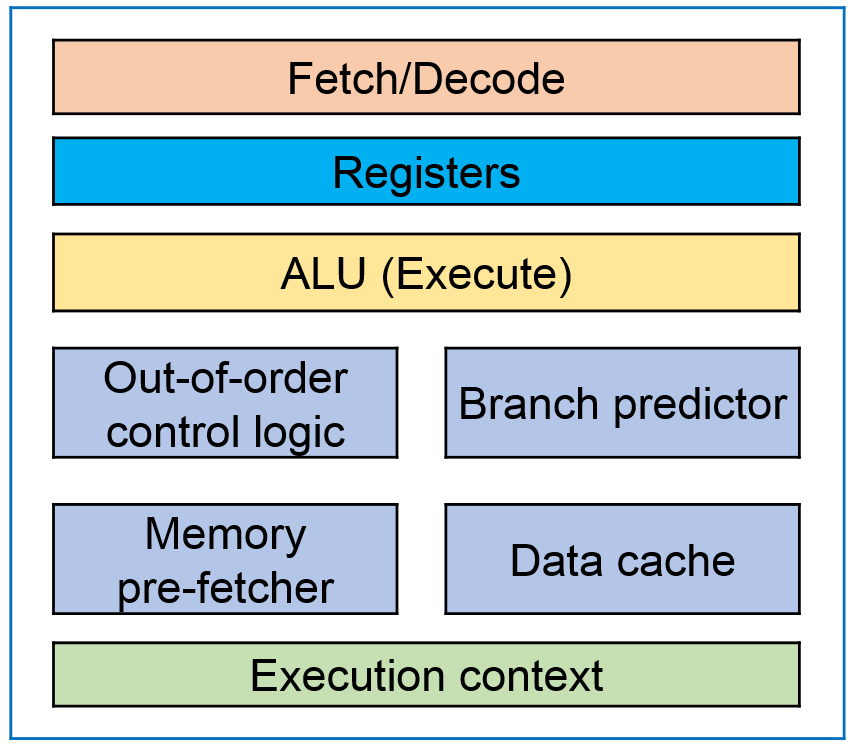
CPU Core
Что здесь особенного? Одно ядро и куча вспомогательных блоков.
А теперь давайте посмотрим на архитектуру GPU:
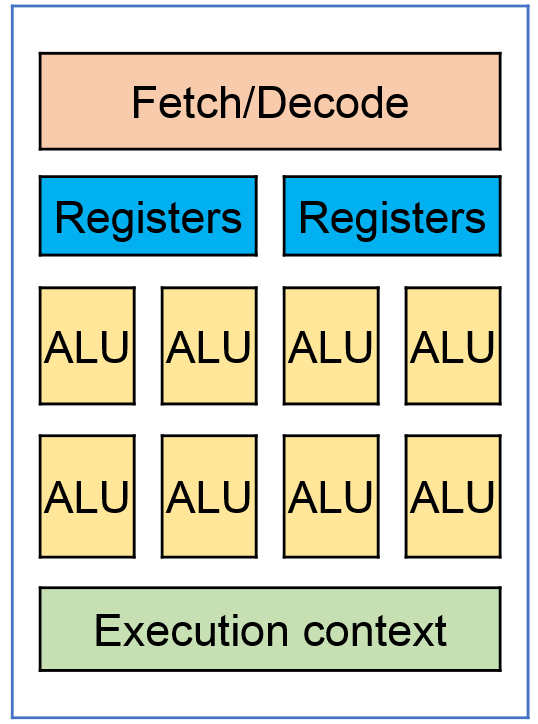
GPU Core
У видеокарты множество вычислительных ядер, обычно несколько тысяч, но они объединены в блоки, для видеокарт NVIDIA обычно по 32, и имеют общие элементы, в т.ч. и регистры. Архитектура ядра GPU и логических элементов существенно проще, чем на CPU, а именно, нет префетчеров, бранч-предикторов и много чего еще.
Что же, это ключевые моменты отличия в архитектуре CPU и GPU, и, собственно, они и накладывают ограничения или, наоборот, открывают возможности к тому, что мы можем эффективно считать на GPU.
Я не упомянул еще один важный момент, обычно, видеокарта и процессор не «шарят» память между собой и записать данные на видеокарту и считать результат обратно — это отдельные операции и могут оказаться «бутылочным горлышком» в вашей системе, график зависимости времени перекачки от размера данных приведен далее в статье.
Какие ограничения накладывает такая архитектура на выполняемые алгоритмы:
Какие возможности открывает:
У нас есть два массива, A и B, и мы хотим к каждому элементу массива A добавить элемент из массива B. Ниже приведен пример на C, хотя, надеюсь, он будет понятен и тем, кто не владеет этим языком:
Классический обход элементов в цикле и линейное время выполнения.
А теперь посмотрим, как такой код будет выглядеть для GPU:
А вот здесь уже интересно, появилась переменная threadIdx, которую мы вроде бы нигде не объявляли. Да, нам предоставляет ее система. Представьте, что в предыдущем примере массив состоит из трех элементов, и вы хотите его запустить в трех параллельных потоках. Для этого вам бы понадобилось добавить еще один параметр – индекс или номер потока. Вот это и делает за нас видеокарта, правда она передает индекс как статическую переменную и может работать сразу с несколькими измерениями – x, y, z.
Еще один нюанс, если вы собираетесь запускать сразу большое количество параллельных потоков, то потоки придется разбить на блоки (архитектурная особенность видеокарт). Максимальный размер блока зависит от видеокарты, а индекс элемента, для которого выполняем вычисления, нужно будет получать так:
В итоге что мы имеем: множество параллельно работающих потоков, выполняющих один и тот же код, но с разными индексами, а соответственно, и данными, т.е. тот самый SIMD.
Это простейший пример, но, если вы хотите работать с GPU, вашу задачу нужно привести к такому же виду. К сожалению, это не всегда возможно и в некоторых случаях может стать темой докторской диссертации, но тем не менее классические алгоритмы все же можно привести к такому виду.
Давайте теперь посмотрим, как будет выглядеть агрегация, приведенная к SIMD представлению:
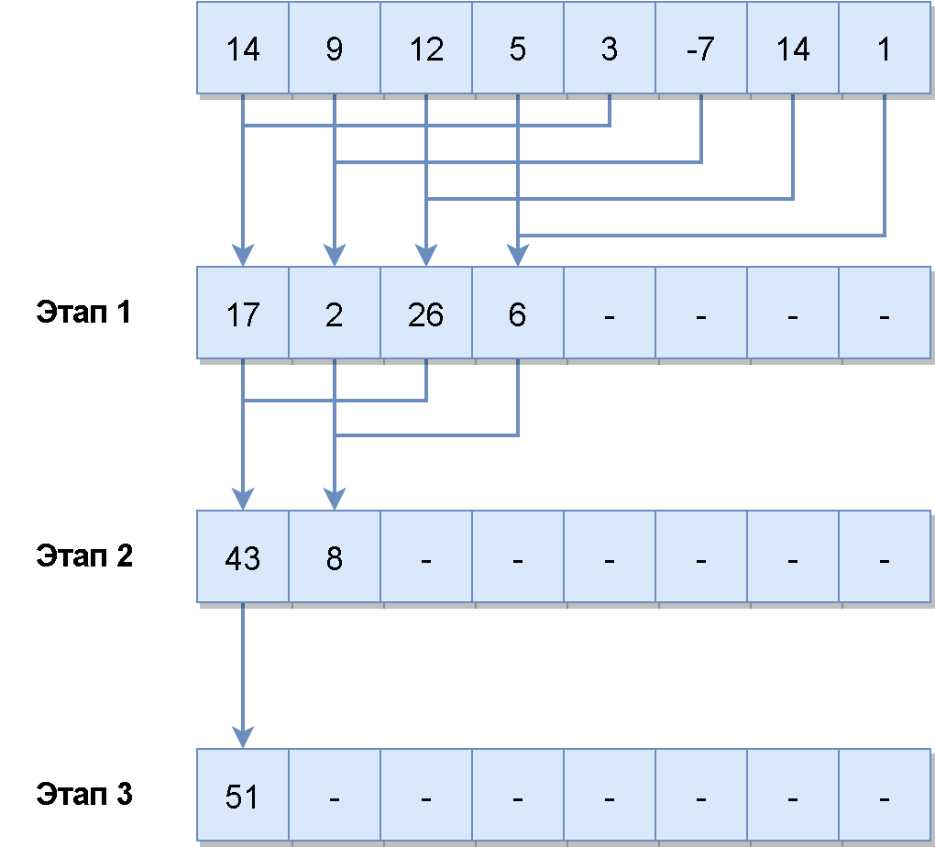
У нас есть массив из n элементов. На первом этапе мы запускаем n/2 потоков и каждый поток складывает по два элемента, т.е. за одну итерацию мы складываем между собой половину элементов в массиве. А дальше в цикле повторяем все тоже самое для вновь получившегося массива, пока не сагрегируем два последних элемента. Как видите, чем меньше размер массива, тем меньше параллельных потоков мы можем запустить, т.е. на GPU имеет смысл агрегировать массивы достаточно большого размера. Такой алгоритм можно применять для вычисления суммы элементов (кстати, не забывайте о возможном переполнении типа данных, с которым вы работаете), поиска максимума, минимума или просто поиска.
А вот с сортировкой уже все выглядит намного сложнее.
Два наиболее популярных алгоритма сортировки на GPU это:
Но radix-sort все же используется чаще, и в некоторых библиотеках можно найти production-ready имплементацию. Я не буду детально разбирать, как работают эти алгоритмы, интересующиеся могут найти описание radix-sort по ссылкам https://www.codeproject.com/Articles/543451/Parallel-Radix-Sort-on-the-GPU-using-Cplusplus-AMP и https://stackoverflow.com/a/26229897
Но идея в том, что даже такой нелинейный алгоритм, как сортировка, можно привести к SIMD-виду.
А теперь, прежде чем посмотреть на реальные цифры, которые можно получить от GPU, давайте разберемся, как же все-таки программировать под это чудо техники?
Наиболее распространены две технологии, которые можно использовать для программирования под GPU:
OpenCL – это стандарт, который поддерживают большинство производителей видеокарт, в т.ч. и на мобильных устройствах, также код, написанный на OpenCL, можно запускать на CPU.
Использовать OpenCL можно из C/C++, есть биндинги к другим языкам.
По OpenCL мне больше всего понравилась книга «OpenCL in Action». В ней же описаны разные алгоритмы на GPU, в т.ч. Bitonic-sort и Radix-sort.
CUDA – это проприетарная технология и SDK от компании NVIDIA. Писать можно на C/C++ или использовать биндинги к другим языкам.
Сравнивать OpenCL и CUDA несколько не корректно, т.к. одно — стандарт, второе — целое SDK. Тем не менее многие выбирают CUDA для разработки под видеокарты несмотря на то, что технология проприетарная, хоть и бесплатная и работает только на картах NVIDIA. Тому есть несколько причин:
К особенностям стоит отнести то, что CUDA поставляется с собственным компилятором, который так же может скомпилировать стандартный C/C++ код.
Наиболее полноценной книгой по CUDA, на которую я наткнулся, была «Professional CUDA C Programming», хоть уже и немного устарела, тем не менее в ней рассматривается много технических нюансов программирования для карт NVIDIA.
А что, если я не хочу тратить пару месяцев на чтение этих книг, написание собственной программы для видеокарты тестирование и отладку, а потом выяснить, что это все не для меня?
Как я уже сказал, есть большое количество библиотек, которые скрывают сложности разработки под GPU: XGBoost, cuBLAS, TensorFlow, PyTorch и другие, мы рассмотрим библиотеку thrust, так как она менее специализирована, чем другие вышеприведенные библиотеки, но при этом в ней реализованы базовые алгоритмы, например, сортировка, поиск, агрегация, и с большой вероятностью она может быть применима в ваших задачах.
Thrust – это С++ библиотека, которая ставит своей целью «подменить» стандартные STL алгоритмы на алгоритмы выполняемые на GPU. Например, сортировка массива чисел с помощью этой библиотеки на видеокарте будет выглядеть так:
(не забываем, что пример нужно компилировать компилятором от NVIDIA)
Как видите, thrust::sort очень похож на аналогичный алгоритм из STL. Эта библиотека скрывает много сложностей, в особенности разработку подпрограммы (точнее ядра), которая будет выполняться на видеокарте, но при этом лишает гибкости. Например, если мы хотим отсортировать несколько гигабайт данных, логично было бы отправить кусок данных на карту запустить сортировку, и пока выполняется сортировка, дослать еще данные на карту. Такой подход называется latency hiding и позволяет более эффективно использовать ресурсы серверной карты, но, к сожалению, когда мы используем высокоуровневые библиотеки, такие возможности остаются скрытыми. Но для прототипирования и замера производительности как раз таки подходят, в особенности с thrust можно замерить, какой оверхед дает пересылка данных.
Я написал небольшой бенчмарк с использованием этой библиотеки, который выполняет несколько популярных алгоритмов с разным объемом данных на GPU, давайте посмотрим, какие результаты получились.
Для тестирования GPU я взял инстанс в AWS с видеокартой Tesla k80, это далеко не самая мощная серверная карта на сегодняшний день (самая мощная Tesla v100), но наиболее доступная и имеет на борту:
И для тестов на CPU я взял инстанс с процессором Intel Xeon CPU E5-2686 v4 @ 2.30GHz
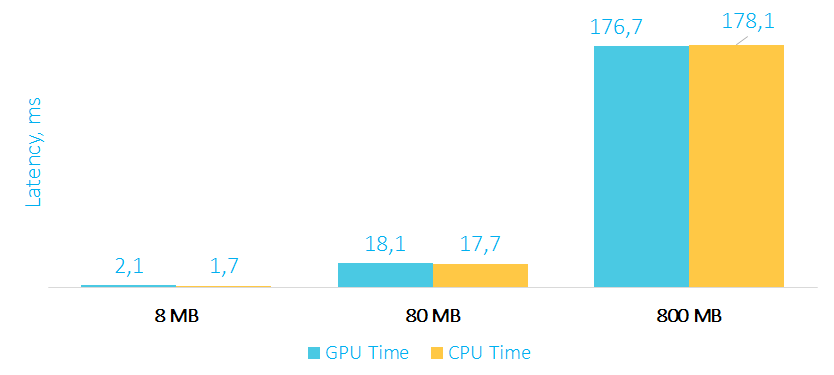
Время выполнения трансформации на GPU и CPU в мс
Как видите, обычная трансформация элементов массива выполняется по времени примерно одинаково, как на GPU, так и на CPU. А все почему? Потому что оверхед на пересылку данных на карту и обратно съедает весь performance boost (про оверхед мы поговорим отдельно), да и вычислений на карте выполняется относительно немного. К тому же не стоит забывать, что процессоры также поддерживают SIMD инструкции, и компиляторы в простых случаях могут эффективно их задействовать.
Давайте теперь посмотрим, насколько эффективно выполняется агрегация на GPU.
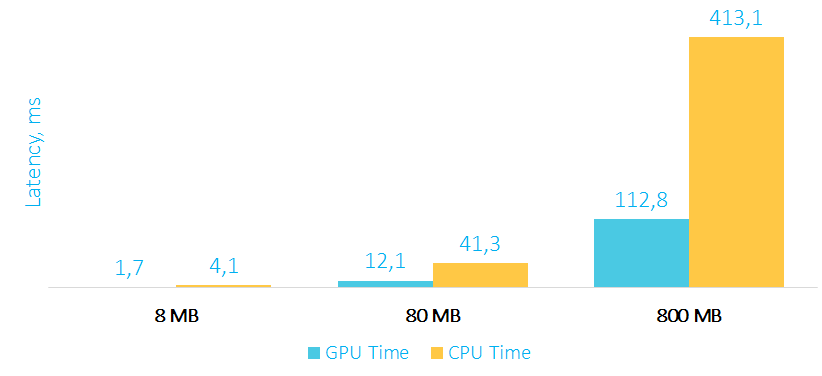
Время выполнения агрегации на GPU и CPU в мс
В примере с агрегацией мы уже видим существенный прирост производительности с увеличением объема данных. Стоит также обратить внимание на то, что в память карты мы перекачиваем большой объем данных, а назад забираем только одно агрегированное значение, т.е. оверхед на пересылку данных из карты в RAM минимален.
Перейдем к самому интересному примеру – сортировке.

Время выполнения сортировки на GPU и CPU в мс
Несмотря на то, что мы пересылаем на видеокарту и обратно весь массив данных, сортировка на GPU 800 MB данных выполняется примерно в 25 раз быстрее, чем на процессоре.
Как видно из примера с трансформацией, не всегда очевидно, будет ли GPU эффективен даже в тех задачах, которые хорошо параллелятся. Причиной тому — оверхед на пересылку данных из оперативной памяти компьютера в память видеокарты (в игровых консолях, кстати, память расшарена между CPU и GPU, и нет необходимости пересылать данные). Одна из характеристик видеокарты это — memory bandwidth или пропускная способность памяти, которая определяет теоретическую пропускную способность карты. Для Tesla k80 это 480 GB/s, для Tesla v100 это уже 900 GB/s. Также на пропускную способность будет влиять версия PCI Express и имплементация того, как вы будете передавать данные на карту, например, это можно делать в несколько параллельных потоков.
Давайте посмотрим на практические результаты, которые удалось получить для видеокарты Tesla k80 в облаке Amazon:
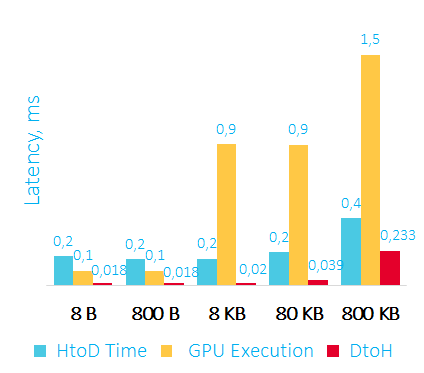
Время пересылки данных на GPU, сортировки и пересылки данных обратно в RAM в мс
HtoD – передаем данные на видеокарту
GPU Execution – сортировка на видеокарте
DtoH – копирование данных из видеокарты в оперативную память
Первое, что можно отметить – считывать данные из видеокарты получается быстрее, чем записывать их туда.
Второе – при работе с видеокартой можно получить latency от 350 микросекунд, а этого уже может хватить для некоторых low latency приложений.
Ниже на графике приведен оверхед для большего объема данных:
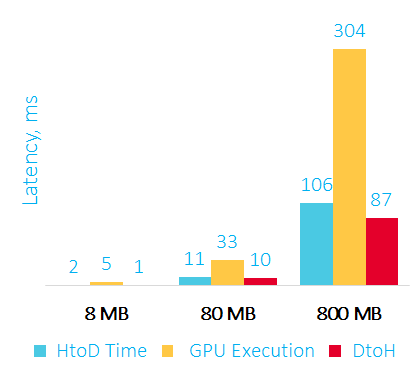
Время пересылки данных на GPU, сортировки и пересылки данных обратно в RAM в мс
Наиболее частый вопрос — чем отличается игровая видеокарта от серверной? По характеристикам они очень похожи, а цены отличаются в разы.

Основные отличия серверной (NVIDIA) и игровой карты:
Это, пожалуй, основные важные отличия, которые я нашел.
После того как мы разобрались, как запустить простейший алгоритм на видеокарте и каких результатов можно ожидать, следующий логичный вопрос, а как будет себя вести видеокарта при обработке нескольких параллельных запросов. В качестве ответа у меня есть два графика выполнения вычислений на GPU и процессоре с 4-мя и 32-мя ядрами:
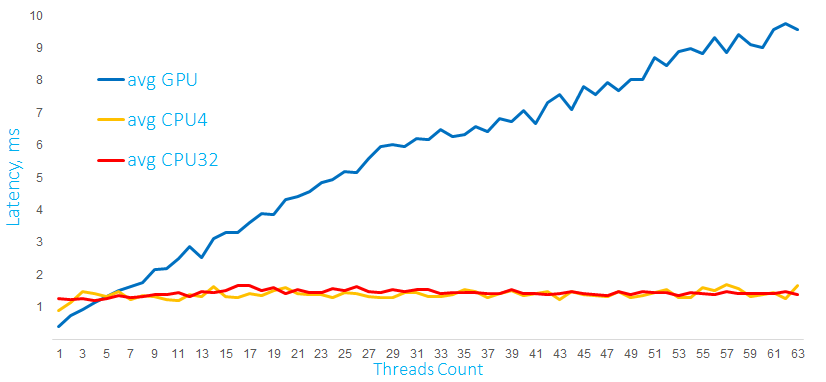
Время выполнения математических расчетов на GPU и CPU c матрицами размером 1000 x 60 в мс
На этом графике выполняются расчеты с матрицами размером 1000 x 60 элементов. Запускаются вычисления из нескольких программных потоков, для GPU дополнительно создается отдельный stream для каждого CPU-потока (используется тот самый Hyper-Q).
Как видно, процессор справляется с такой нагрузкой очень хорошо, при этом latency для одного запроса на GPU существенно растет с увеличением числа параллельных запросов.
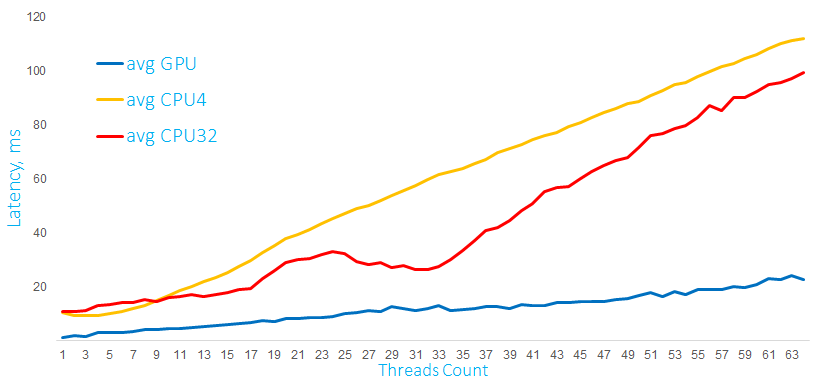
Время выполнения математических расчетов на GPU и CPU c матрицами 10 000 x 60 в мс
На втором графике те же самые вычисления, но с матрицами в 10 раз больше, и GPU под такой нагрузкой ведет себя существенно лучше. Эти графики очень показательны, и можно сделать вывод: поведение под нагрузкой зависит от характера самой нагрузки. Процессор может также довольно эффективно справляться с матричными вычислениями, но до определенных пределов. Для видеокарты характерно то, что для небольшой вычислительной нагрузки производительность падает примерно линейно. С увеличением нагрузки и количества параллельных потоков видеокарта справляется уже лучше.
Сложно строить гипотезы, как будет себя вести GPU в различных ситуациях, но, как видите, при определенных условиях серверная карта может достаточно эффективно обрабатывать запросы из нескольких параллельных потоков.
Обсудим еще несколько вопросов, которые могут возникнуть у вас, если вы все-таки решили использовать GPU в своих проектах.
Как мы уже говорили, два основных ресурса видеокарты – это вычислительные ядра и память.
К примеру, у нас несколько процессов или контейнеров, использующих видеокарту, и хотелось бы иметь возможность поделить видеокарту между ними. К сожалению, простого API для этого нет. NVIDIA предлагает технологию vGPU, но карту Tesla k80 я не нашел в списке поддерживаемых, и насколько мне удалось понять из описания, технология больше заточена на виртуальные дисплеи, чем на вычисления. Возможно, AMD предлагает что-то более подходящее.
Поэтому, если планируете использовать GPU в своих проектах, стоит рассчитывать на то, что приложение будет использовать видеокарту монопольно, либо вы будете программно контролировать объем выделяемой памяти и количество ядер, используемых для вычислений.
Если с ограничением ресурсов вы разобрались, то следующий логичный вопрос: а если в сервере несколько видеокарт?
Опять же, можно на уровне приложения решать, какой GPU оно будет использовать.
Другой более удобный способ – это Docker-контейнеры. Можно использовать и обычные контейнеры, но NVIDIA предлагает свои контейнеры NGC, с оптимизированными версиями различного софта, библиотек и драйверов. Для одного контейнера можно ограничить количество используемых GPU и их видимость для контейнера. Оверхед на использования контейнера около 3%.
Другой вопрос, что делать, если вы хотите выполнять одну задачу на нескольких GPU в рамках одного сервера или кластера?
Если вы выбрали библиотеку на подобии thrust или более низкоуровневое решение, то задачу придется решать вручную. Высокоуровневые фреймворки, например, для машинного обучения или нейронных сетей, обычно поддерживают возможность использования нескольких карт из коробки.
Дополнительно хотелось бы отметить то, что, например, NVIDIA предлагает интерфейс прямого обмена данными между картами – NVLINK, который существенно быстрее чем PCI Express. И есть технология прямого доступа к памяти карты из других PCI Express устройств – GPUDirect RDMA, в т.ч. и сетевых.
Если вы размышляете об использовании GPU в своих проектах, то GPU, скорее всего, вам подойдет если:
Заранее также стоит задаться вопросами:
На этом все, надеюсь, материал будет вам полезен и поможет принять верное решение!
Бенчмарк и результаты на github — https://github.com/tishden/gpu_benchmark/tree/master/cuda
В дополнение к теме запись доклада «Базы данных на GPU – архитектура, производительность и перспективы использования»
Вебинар NVIDIA по NGC-контейнерам — http://bit.ly/2UmVIVt или http://bit.ly/2x4vJKF

Статья написана по мотивам моего выступления на HighLoad++. В ней рассматриваются в основном технологии, предлагаемые компанией NVIDIA. У меня нет цели рекламировать какие-либо продукты, я лишь привожу их в качестве примера, и наверняка что-то похожее можно найти у конкурирующих производителей.
Зачем что-то считать на GPU?
Два процессора можно сравнить по разным критериям, наверное, самые популярные — это частота и количество ядер, размер кэшей и прочее, но в конечном счете, нас интересует, сколько операций процессор может выполнить за единицу времени, что это за операции вопрос отдельный, но наиболее распространенной метрикой является количество операций с плавающей запятой в секунду — flops. И когда мы хотим сравнить теплое с мягким, а в нашем случае GPU с CPU, эта метрика приходится как нельзя кстати.
Ниже на графике изображены рост этих самых флопсов с течением времени для процессоров и для видеокарт.

(Данные собраны из открытых источников, нет данных за 2019-20 годы, т.к. там не все так красиво, но GPU все-таки выигрывают)
Что ж, заманчиво, не правда ли? Перекладываем все вычисления с CPU на GPU и получаем в восемь раз лучшую производительность!
Но, конечно же, не все так просто. Нельзя просто так взять и переложить все на GPU, о том почему, мы поговорим дальше.
Архитектура GPU и ее сравнение с CPU
Привожу многим знакомую картинку с архитектурой CPU и основными элементами:

CPU Core
Что здесь особенного? Одно ядро и куча вспомогательных блоков.
А теперь давайте посмотрим на архитектуру GPU:

GPU Core
У видеокарты множество вычислительных ядер, обычно несколько тысяч, но они объединены в блоки, для видеокарт NVIDIA обычно по 32, и имеют общие элементы, в т.ч. и регистры. Архитектура ядра GPU и логических элементов существенно проще, чем на CPU, а именно, нет префетчеров, бранч-предикторов и много чего еще.
Что же, это ключевые моменты отличия в архитектуре CPU и GPU, и, собственно, они и накладывают ограничения или, наоборот, открывают возможности к тому, что мы можем эффективно считать на GPU.
Я не упомянул еще один важный момент, обычно, видеокарта и процессор не «шарят» память между собой и записать данные на видеокарту и считать результат обратно — это отдельные операции и могут оказаться «бутылочным горлышком» в вашей системе, график зависимости времени перекачки от размера данных приведен далее в статье.
Ограничения и возможности при работе с GPU
Какие ограничения накладывает такая архитектура на выполняемые алгоритмы:
- Если мы выполняем расчет на GPU, то не можем выделить только одно ядро, выделен будет целый блок ядер (32 для NVIDIA).
- Все ядра выполняют одни и те же инструкции, но с разными данными (поговорим про это дальше), такие вычисления называются Single-Instruction-Multiple-Data или SIMD (хотя NVIDIA вводит свое уточнение).
- Из-за относительно простого набора логических блоков и общих регистров, GPU очень не любит ветвлений, да и в целом сложной логики в алгоритмах.
Какие возможности открывает:
- Собственно, ускорение тех самых SIMD-вычислений. Простейшим примером может служить поэлементное сложение матриц, его и давайте разберем.
Приведение классических алгоритмов к SIMD-представлению
Трансформация
У нас есть два массива, A и B, и мы хотим к каждому элементу массива A добавить элемент из массива B. Ниже приведен пример на C, хотя, надеюсь, он будет понятен и тем, кто не владеет этим языком:
void func(float *A, float *B, size)
{
for (int i = 0; i < size; i++)
{
A[i] += B[i]
}
}
Классический обход элементов в цикле и линейное время выполнения.
А теперь посмотрим, как такой код будет выглядеть для GPU:
void func(float *A, float *B, size)
{
int i = threadIdx.x;
if (i < size)
A[i] += B[i]
}
А вот здесь уже интересно, появилась переменная threadIdx, которую мы вроде бы нигде не объявляли. Да, нам предоставляет ее система. Представьте, что в предыдущем примере массив состоит из трех элементов, и вы хотите его запустить в трех параллельных потоках. Для этого вам бы понадобилось добавить еще один параметр – индекс или номер потока. Вот это и делает за нас видеокарта, правда она передает индекс как статическую переменную и может работать сразу с несколькими измерениями – x, y, z.
Еще один нюанс, если вы собираетесь запускать сразу большое количество параллельных потоков, то потоки придется разбить на блоки (архитектурная особенность видеокарт). Максимальный размер блока зависит от видеокарты, а индекс элемента, для которого выполняем вычисления, нужно будет получать так:
int i = blockIdx.x * blockDim.x + threadIdx.x; // blockIdx – индекс блока, blockDim – размер блока, threadIdx – индекс потока в блоке
В итоге что мы имеем: множество параллельно работающих потоков, выполняющих один и тот же код, но с разными индексами, а соответственно, и данными, т.е. тот самый SIMD.
Это простейший пример, но, если вы хотите работать с GPU, вашу задачу нужно привести к такому же виду. К сожалению, это не всегда возможно и в некоторых случаях может стать темой докторской диссертации, но тем не менее классические алгоритмы все же можно привести к такому виду.
Агрегация
Давайте теперь посмотрим, как будет выглядеть агрегация, приведенная к SIMD представлению:

У нас есть массив из n элементов. На первом этапе мы запускаем n/2 потоков и каждый поток складывает по два элемента, т.е. за одну итерацию мы складываем между собой половину элементов в массиве. А дальше в цикле повторяем все тоже самое для вновь получившегося массива, пока не сагрегируем два последних элемента. Как видите, чем меньше размер массива, тем меньше параллельных потоков мы можем запустить, т.е. на GPU имеет смысл агрегировать массивы достаточно большого размера. Такой алгоритм можно применять для вычисления суммы элементов (кстати, не забывайте о возможном переполнении типа данных, с которым вы работаете), поиска максимума, минимума или просто поиска.
Сортировка
А вот с сортировкой уже все выглядит намного сложнее.
Два наиболее популярных алгоритма сортировки на GPU это:
- Bitonic-sort
- Radix-sort
Но radix-sort все же используется чаще, и в некоторых библиотеках можно найти production-ready имплементацию. Я не буду детально разбирать, как работают эти алгоритмы, интересующиеся могут найти описание radix-sort по ссылкам https://www.codeproject.com/Articles/543451/Parallel-Radix-Sort-on-the-GPU-using-Cplusplus-AMP и https://stackoverflow.com/a/26229897
Но идея в том, что даже такой нелинейный алгоритм, как сортировка, можно привести к SIMD-виду.
А теперь, прежде чем посмотреть на реальные цифры, которые можно получить от GPU, давайте разберемся, как же все-таки программировать под это чудо техники?
C чего начать
Наиболее распространены две технологии, которые можно использовать для программирования под GPU:
- OpenCL
- CUDA
OpenCL – это стандарт, который поддерживают большинство производителей видеокарт, в т.ч. и на мобильных устройствах, также код, написанный на OpenCL, можно запускать на CPU.
Использовать OpenCL можно из C/C++, есть биндинги к другим языкам.
По OpenCL мне больше всего понравилась книга «OpenCL in Action». В ней же описаны разные алгоритмы на GPU, в т.ч. Bitonic-sort и Radix-sort.
CUDA – это проприетарная технология и SDK от компании NVIDIA. Писать можно на C/C++ или использовать биндинги к другим языкам.
Сравнивать OpenCL и CUDA несколько не корректно, т.к. одно — стандарт, второе — целое SDK. Тем не менее многие выбирают CUDA для разработки под видеокарты несмотря на то, что технология проприетарная, хоть и бесплатная и работает только на картах NVIDIA. Тому есть несколько причин:
- Более продвинутое API
- Проще синтаксис и инициализация карты
- Подпрограмма, выполняемая на GPU, является частью исходных текстов основной (host) программы
- Собственный профайлер, в т.ч. и визуальный
- Большое количество готовых библиотек
- Более живое комьюнити
К особенностям стоит отнести то, что CUDA поставляется с собственным компилятором, который так же может скомпилировать стандартный C/C++ код.
Наиболее полноценной книгой по CUDA, на которую я наткнулся, была «Professional CUDA C Programming», хоть уже и немного устарела, тем не менее в ней рассматривается много технических нюансов программирования для карт NVIDIA.
А что, если я не хочу тратить пару месяцев на чтение этих книг, написание собственной программы для видеокарты тестирование и отладку, а потом выяснить, что это все не для меня?
Как я уже сказал, есть большое количество библиотек, которые скрывают сложности разработки под GPU: XGBoost, cuBLAS, TensorFlow, PyTorch и другие, мы рассмотрим библиотеку thrust, так как она менее специализирована, чем другие вышеприведенные библиотеки, но при этом в ней реализованы базовые алгоритмы, например, сортировка, поиск, агрегация, и с большой вероятностью она может быть применима в ваших задачах.
Thrust – это С++ библиотека, которая ставит своей целью «подменить» стандартные STL алгоритмы на алгоритмы выполняемые на GPU. Например, сортировка массива чисел с помощью этой библиотеки на видеокарте будет выглядеть так:
thrust::host_vector<DataType> h_vec(size); // объявляем обычный массив элементов
std::generate(h_vec.begin(), h_vec.end(), rand); // заполняем случайными значениями
thrust::device_vector<DataType> d_vec = h_vec; // пересылаем данные из оперативной памяти в память видеокарты
thrust::sort(d_vec.begin(), d_vec.end()); // сортируем данные на видеокарте
thrust::copy(d_vec.begin(), d_vec.end(), h_vec.begin()); // копируем данные назад, из видеокарты в оперативную память
(не забываем, что пример нужно компилировать компилятором от NVIDIA)
Как видите, thrust::sort очень похож на аналогичный алгоритм из STL. Эта библиотека скрывает много сложностей, в особенности разработку подпрограммы (точнее ядра), которая будет выполняться на видеокарте, но при этом лишает гибкости. Например, если мы хотим отсортировать несколько гигабайт данных, логично было бы отправить кусок данных на карту запустить сортировку, и пока выполняется сортировка, дослать еще данные на карту. Такой подход называется latency hiding и позволяет более эффективно использовать ресурсы серверной карты, но, к сожалению, когда мы используем высокоуровневые библиотеки, такие возможности остаются скрытыми. Но для прототипирования и замера производительности как раз таки подходят, в особенности с thrust можно замерить, какой оверхед дает пересылка данных.
Я написал небольшой бенчмарк с использованием этой библиотеки, который выполняет несколько популярных алгоритмов с разным объемом данных на GPU, давайте посмотрим, какие результаты получились.
Результаты выполнения алгоритмов на GPU
Для тестирования GPU я взял инстанс в AWS с видеокартой Tesla k80, это далеко не самая мощная серверная карта на сегодняшний день (самая мощная Tesla v100), но наиболее доступная и имеет на борту:
- 4992 CUDA ядра
- 24 GB памяти
- 480 Gb/s — пропускная способность памяти
И для тестов на CPU я взял инстанс с процессором Intel Xeon CPU E5-2686 v4 @ 2.30GHz
Трансформация
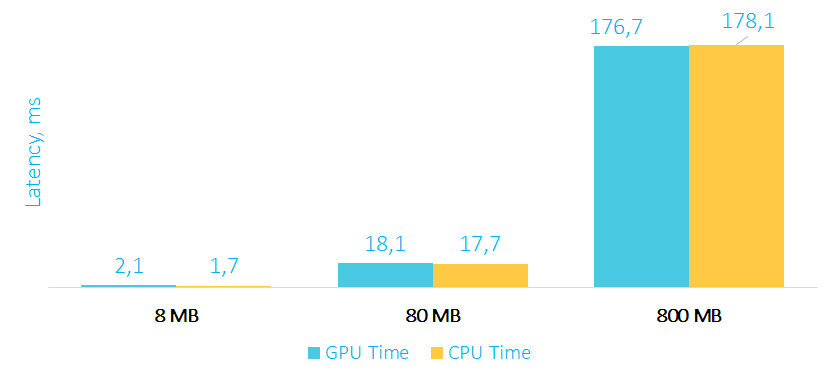
Время выполнения трансформации на GPU и CPU в мс
Как видите, обычная трансформация элементов массива выполняется по времени примерно одинаково, как на GPU, так и на CPU. А все почему? Потому что оверхед на пересылку данных на карту и обратно съедает весь performance boost (про оверхед мы поговорим отдельно), да и вычислений на карте выполняется относительно немного. К тому же не стоит забывать, что процессоры также поддерживают SIMD инструкции, и компиляторы в простых случаях могут эффективно их задействовать.
Давайте теперь посмотрим, насколько эффективно выполняется агрегация на GPU.
Агрегация

Время выполнения агрегации на GPU и CPU в мс
В примере с агрегацией мы уже видим существенный прирост производительности с увеличением объема данных. Стоит также обратить внимание на то, что в память карты мы перекачиваем большой объем данных, а назад забираем только одно агрегированное значение, т.е. оверхед на пересылку данных из карты в RAM минимален.
Перейдем к самому интересному примеру – сортировке.
Сортировка

Время выполнения сортировки на GPU и CPU в мс
Несмотря на то, что мы пересылаем на видеокарту и обратно весь массив данных, сортировка на GPU 800 MB данных выполняется примерно в 25 раз быстрее, чем на процессоре.
Оверхед на пересылку данных
Как видно из примера с трансформацией, не всегда очевидно, будет ли GPU эффективен даже в тех задачах, которые хорошо параллелятся. Причиной тому — оверхед на пересылку данных из оперативной памяти компьютера в память видеокарты (в игровых консолях, кстати, память расшарена между CPU и GPU, и нет необходимости пересылать данные). Одна из характеристик видеокарты это — memory bandwidth или пропускная способность памяти, которая определяет теоретическую пропускную способность карты. Для Tesla k80 это 480 GB/s, для Tesla v100 это уже 900 GB/s. Также на пропускную способность будет влиять версия PCI Express и имплементация того, как вы будете передавать данные на карту, например, это можно делать в несколько параллельных потоков.
Давайте посмотрим на практические результаты, которые удалось получить для видеокарты Tesla k80 в облаке Amazon:
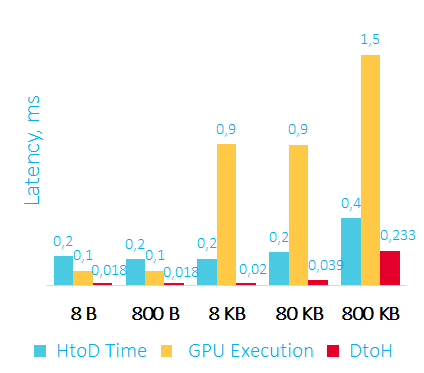
Время пересылки данных на GPU, сортировки и пересылки данных обратно в RAM в мс
HtoD – передаем данные на видеокарту
GPU Execution – сортировка на видеокарте
DtoH – копирование данных из видеокарты в оперативную память
Первое, что можно отметить – считывать данные из видеокарты получается быстрее, чем записывать их туда.
Второе – при работе с видеокартой можно получить latency от 350 микросекунд, а этого уже может хватить для некоторых low latency приложений.
Ниже на графике приведен оверхед для большего объема данных:
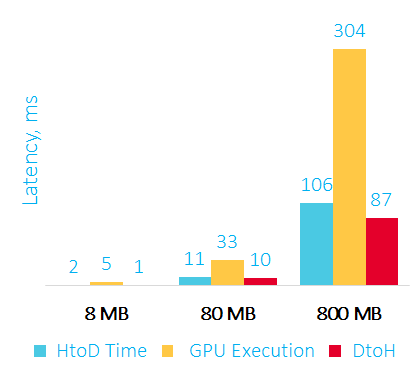
Время пересылки данных на GPU, сортировки и пересылки данных обратно в RAM в мс
Серверное использование
Наиболее частый вопрос — чем отличается игровая видеокарта от серверной? По характеристикам они очень похожи, а цены отличаются в разы.

Основные отличия серверной (NVIDIA) и игровой карты:
- Гарантия производителя (игровая карта не рассчитана на серверное использование)
- Возможные проблемы с виртуализацией для потребительской видеокарты
- Наличие механизма коррекции ошибок на серверной карте
- Количество параллельных потоков (не CUDA ядер) или поддержка Hyper-Q, которая позволяет из нескольких потоков на CPU работать с картой, например, из одного потока закачивать данные на карту, а из другого запускать вычисления
Это, пожалуй, основные важные отличия, которые я нашел.
Многопоточность
После того как мы разобрались, как запустить простейший алгоритм на видеокарте и каких результатов можно ожидать, следующий логичный вопрос, а как будет себя вести видеокарта при обработке нескольких параллельных запросов. В качестве ответа у меня есть два графика выполнения вычислений на GPU и процессоре с 4-мя и 32-мя ядрами:

Время выполнения математических расчетов на GPU и CPU c матрицами размером 1000 x 60 в мс
На этом графике выполняются расчеты с матрицами размером 1000 x 60 элементов. Запускаются вычисления из нескольких программных потоков, для GPU дополнительно создается отдельный stream для каждого CPU-потока (используется тот самый Hyper-Q).
Как видно, процессор справляется с такой нагрузкой очень хорошо, при этом latency для одного запроса на GPU существенно растет с увеличением числа параллельных запросов.

Время выполнения математических расчетов на GPU и CPU c матрицами 10 000 x 60 в мс
На втором графике те же самые вычисления, но с матрицами в 10 раз больше, и GPU под такой нагрузкой ведет себя существенно лучше. Эти графики очень показательны, и можно сделать вывод: поведение под нагрузкой зависит от характера самой нагрузки. Процессор может также довольно эффективно справляться с матричными вычислениями, но до определенных пределов. Для видеокарты характерно то, что для небольшой вычислительной нагрузки производительность падает примерно линейно. С увеличением нагрузки и количества параллельных потоков видеокарта справляется уже лучше.
Сложно строить гипотезы, как будет себя вести GPU в различных ситуациях, но, как видите, при определенных условиях серверная карта может достаточно эффективно обрабатывать запросы из нескольких параллельных потоков.
Обсудим еще несколько вопросов, которые могут возникнуть у вас, если вы все-таки решили использовать GPU в своих проектах.
Ограничение ресурсов
Как мы уже говорили, два основных ресурса видеокарты – это вычислительные ядра и память.
К примеру, у нас несколько процессов или контейнеров, использующих видеокарту, и хотелось бы иметь возможность поделить видеокарту между ними. К сожалению, простого API для этого нет. NVIDIA предлагает технологию vGPU, но карту Tesla k80 я не нашел в списке поддерживаемых, и насколько мне удалось понять из описания, технология больше заточена на виртуальные дисплеи, чем на вычисления. Возможно, AMD предлагает что-то более подходящее.
Поэтому, если планируете использовать GPU в своих проектах, стоит рассчитывать на то, что приложение будет использовать видеокарту монопольно, либо вы будете программно контролировать объем выделяемой памяти и количество ядер, используемых для вычислений.
Контейнеры и GPU
Если с ограничением ресурсов вы разобрались, то следующий логичный вопрос: а если в сервере несколько видеокарт?
Опять же, можно на уровне приложения решать, какой GPU оно будет использовать.
Другой более удобный способ – это Docker-контейнеры. Можно использовать и обычные контейнеры, но NVIDIA предлагает свои контейнеры NGC, с оптимизированными версиями различного софта, библиотек и драйверов. Для одного контейнера можно ограничить количество используемых GPU и их видимость для контейнера. Оверхед на использования контейнера около 3%.
Работа в кластере
Другой вопрос, что делать, если вы хотите выполнять одну задачу на нескольких GPU в рамках одного сервера или кластера?
Если вы выбрали библиотеку на подобии thrust или более низкоуровневое решение, то задачу придется решать вручную. Высокоуровневые фреймворки, например, для машинного обучения или нейронных сетей, обычно поддерживают возможность использования нескольких карт из коробки.
Дополнительно хотелось бы отметить то, что, например, NVIDIA предлагает интерфейс прямого обмена данными между картами – NVLINK, который существенно быстрее чем PCI Express. И есть технология прямого доступа к памяти карты из других PCI Express устройств – GPUDirect RDMA, в т.ч. и сетевых.
Рекомендации
Если вы размышляете об использовании GPU в своих проектах, то GPU, скорее всего, вам подойдет если:
- Вашу задачу можно привести к SIMD-виду
- Есть возможность загрузить большую часть данных на карту до вычислений (закешировать)
- Задача подразумевает интенсивные вычисления
Заранее также стоит задаться вопросами:
- Сколько будет параллельных запросов
- На какое latency вы рассчитываете
- Достаточно ли вам одной карты для вашей нагрузки, нужен сервер с несколькими картами или кластер GPU-серверов
На этом все, надеюсь, материал будет вам полезен и поможет принять верное решение!
Ссылки
Бенчмарк и результаты на github — https://github.com/tishden/gpu_benchmark/tree/master/cuda
В дополнение к теме запись доклада «Базы данных на GPU – архитектура, производительность и перспективы использования»
Вебинар NVIDIA по NGC-контейнерам — http://bit.ly/2UmVIVt или http://bit.ly/2x4vJKF
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Используете ли вы GPU в своих проектах?
31.1% Да65
26.32% Нет55
42.58% Нет, но планирую89
Проголосовали 209 пользователей. Воздержался 41 пользователь.