Оформляя тикет в системе управления проектами и отслеживания задач, каждый из нас рад видеть ориентировочные сроки решения по своему обращению.
Получая поток входящих тикетов, человеку/команде необходимо выстроить их в очередь по приоритету и по времени, которое займет решение каждого обращения.
Все это позволяет эффективнее планировать своё время обеим сторонам.
Под катом я расскажу о том, как проводил анализ и обучал ML модели, предсказывающие время решения оформляемых в нашу команду тикетов.
Сам я работаю на позиции SRE в команде, называющейся LAB. К нам стекаются обращения как от разработчиков, так и от QA касательно разворачивания новых тестовых окружений, их обновления до последних релизных версий, решения различных возникающих проблем и многое другое. Задачи эти довольно разнородные и, что логично, занимают разное количество времени на выполнение. Существует наша команда уже несколько лет и за это время успела накопиться неплохая база обращений. Именно эту базу я решил проанализировать и на её основе, с помощью машинного обучения, составить модель, которая будет заниматься предсказанием вероятного времени закрытия обращения (тикета).
В нашей работе мы используем JIRA, однако представляемая мною в данной статье модель не имеет никакой привязки к конкретному продукту — нужную информацию не составляет проблем получить из любой базы.
Итак, давайте перейдем от слов к делу.
Предварительный анализ данных
Подгружаем всё необходимое и отобразим версии используемых пакетов.
import warnings
warnings.simplefilter('ignore')
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import datetime
from nltk.corpus import stopwords
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from datetime import time, date
for package in [pd, np, matplotlib, sklearn, nltk]:
print(package.__name__, 'version:', package.__version__)pandas version: 0.23.4
numpy version: 1.15.0
matplotlib version: 2.2.2
sklearn version: 0.19.2
nltk version: 3.3Загрузим данные из csv файла. В нем содержится информация о тикетах, закрытых за последние 1.5 года. Прежде чем записать данные в файл они были немного предварительно обработаны. Например, из текстовых полей с описаниями были удалены запятые и точки. Однако это лишь предварительная обработка и в дальнейшем текст будет дополнительно очищен.
Посмотрим, что есть в нашем наборе данных. Всего в него попали 10783 тикета.
| Created | Дата и время создания тикета |
| Resolved | Дата и время закрытия тикета |
| Resolution_time | Количество минут, прошедших между созданием и закрытием тикета. Считается именно календарное время, т.к. у компании есть офисы в разных странах, работающие по разным часовым поясам и фиксированного времени работы всего отдела нет. |
| Engineer_N | «Закодированные» имена инженеров (дабы ненароком не выдать какую-либо личную или конфиденциальную информацию в дальнейшем в статье будет еще не мало «закодированных» данных, которые по сути просто переименованы). В этих полях содержится количество тикетов в режиме «in progress» на момент поступления каждого из тикетов в представленном дата сете. На этих полях я остановлюсь отдельно ближе к концу статьи, т.к. они заслуживают дополнительного внимания. |
| Assignee | Сотрудник, который занимался решением задачи. |
| Issue_type | Тип тикета. |
| Environment | Название тестового рабочего окружения, касательно которого сделан тикет (может значиться как конкретное окружение так и локация в целом, например, датацентр). |
| Priority | Приоритет тикета. |
| Worktype | Вид работы, который ожидается по данному тикету (добавление или удаление серверов, обновление окружения, работа с мониторингом и т.д.) |
| Description | Описание |
| Summary | Заголовок тикета. |
| Watchers | Количество человек, которые «наблюдают» за тикетом, т.е. им приходят уведомления на почту по каждой из активностей в тикете. |
| Votes | Количество человек, «проголосовавших» за тикет, тем самым показав его важность и свою заинтересованность в нем. |
| Reporter | Человек, оформивший тикет. |
| Engineer_N_vacation | Находился ли инженер в отпуске на момент оформления тикета. |
df.info()<class 'pandas.core.frame.DataFrame'>
Index: 10783 entries, ENV-36273 to ENV-49164
Data columns (total 37 columns):
Created 10783 non-null object
Resolved 10783 non-null object
Resolution_time 10783 non-null int64
engineer_1 10783 non-null int64
engineer_2 10783 non-null int64
engineer_3 10783 non-null int64
engineer_4 10783 non-null int64
engineer_5 10783 non-null int64
engineer_6 10783 non-null int64
engineer_7 10783 non-null int64
engineer_8 10783 non-null int64
engineer_9 10783 non-null int64
engineer_10 10783 non-null int64
engineer_11 10783 non-null int64
engineer_12 10783 non-null int64
Assignee 10783 non-null object
Issue_type 10783 non-null object
Environment 10771 non-null object
Priority 10783 non-null object
Worktype 7273 non-null object
Description 10263 non-null object
Summary 10783 non-null object
Watchers 10783 non-null int64
Votes 10783 non-null int64
Reporter 10783 non-null object
engineer_1_vacation 10783 non-null int64
engineer_2_vacation 10783 non-null int64
engineer_3_vacation 10783 non-null int64
engineer_4_vacation 10783 non-null int64
engineer_5_vacation 10783 non-null int64
engineer_6_vacation 10783 non-null int64
engineer_7_vacation 10783 non-null int64
engineer_8_vacation 10783 non-null int64
engineer_9_vacation 10783 non-null int64
engineer_10_vacation 10783 non-null int64
engineer_11_vacation 10783 non-null int64
engineer_12_vacation 10783 non-null int64
dtypes: float64(12), int64(15), object(10)
memory usage: 3.1+ MBИтого у нас 10 "объектных" полей (т.е. содержащих в себе текстовое значение) и 27 числовых полей.
Первым делом сразу же поищем выбросы в наших данных. Как видно есть такие тикеты, у которых время решения исчисляется миллионами минут. Это явно не релевантная информация, такие данные будут лишь мешать строить модель. Попали они сюда, поскольку сбор данных из JIRA производился запросом по полю Resolved, а не Created. Соответственно попали сюда те тикеты, которые были закрыты за последние 1.5 года, однако открыты они могли быть намного намного раньше. Настало время избавиться от них. Отбросим те тикеты, что были созданы ранее 1 июня 2017 года. У нас останется 9493 тикета.
Что же касается причин — думаю в каждом проекте можно с легкостью найти такие запросы, которые болтаются уже довольно продолжительное время ввиду разных обстоятельств и чаще закрываются не по решению самой проблемы, а за "истечением срока давности".
df[['Created', 'Resolved', 'Resolution_time']].sort_values('Resolution_time', ascending=False).head()
df = df[df['Created'] >= '2017-06-01 00:00:00']
print(df.shape)(9493, 33)Итак, давайте начнем смотреть, что интересного мы сможем найти в наших данных. Для начала выведем самое простое — самые популярные окружения среди наших тикетов, самые активные "репортеры" и тому подобное.
df.describe(include=['object'])
df['Environment'].value_counts().head(10)Environment_104 442
ALL 368
Location02 367
Environment_99 342
Location03 342
Environment_31 322
Environment_14 254
Environment_1 232
Environment_87 227
Location01 202
Name: Environment, dtype: int64df['Reporter'].value_counts().head()Reporter_16 388
Reporter_97 199
Reporter_04 147
Reporter_110 145
Reporter_133 138
Name: Reporter, dtype: int64df['Worktype'].value_counts()Support 2482
Infrastructure 1655
Update environment 1138
Monitoring 388
QA 300
Numbers 110
Create environment 95
Tools 62
Delete environment 24
Name: Worktype, dtype: int64df['Priority'].value_counts().plot(kind='bar', figsize=(12,7), rot=0, fontsize=14, title='Распределение тикетов по приоритету');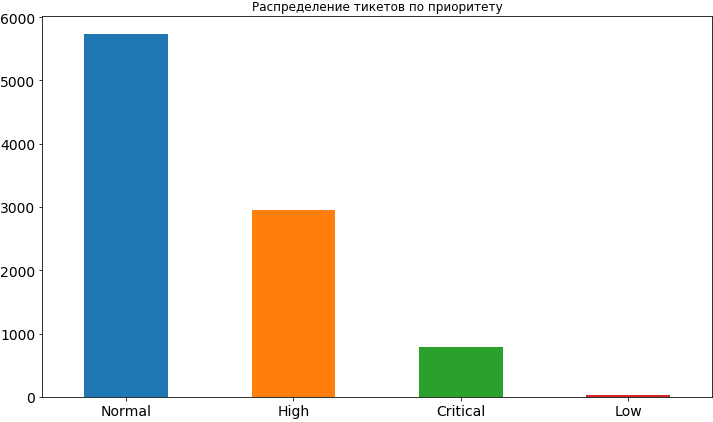
Ну что ж, кое-что мы уже почерпнули. Чаще всего приоритет у тикетов нормальный, примерно в 2 раза реже высокий и еще реже критический. Совсем редко встречается низкий приоритет, видимо люди опасаются его выставлять, считая, что в таком случае он будет довольно долго висеть в очереди и время его решения может затянуться. Позже, когда мы уже построим модель и будем анализировать её результаты мы увидим, что такие опасения могут быть небезосновательными, поскольку низкий приоритет действительно влияет на сроки выполнения задачи и, конечно же, не в сторону ускорения.
Из колонок по самым популярным окружениям и самым активным репортерам мы видим, что с большим отрывом идет Reporter_16, а по окружениям на первом месте Environment_104. Даже если вы еще не догадались, то я открою небольшой секрет — этот репортер из команды, работающей именно над этим окружением.
Давайте посмотрим по какому окружению чаще всего приходят критичные тикеты.
df[df['Priority'] == 'Critical']['Environment'].value_counts().index[0]'Environment_91'А теперь выведем информацию по тому, сколько с этого же самого "критичного" окружения приходится тикетов с другими приоритетами.
df[df['Environment'] == df[df['Priority'] == 'Critical']['Environment'].value_counts().index[0]]['Priority'].value_counts()High 62
Critical 57
Normal 46
Name: Priority, dtype: int64Посмотрим на время выполнения тикета в разрезе по приоритетам. Например, забавно заметить, что среднее время выполнения тикета с низким приоритетом больше 70 тысяч минут (почти 1.5 месяца). Так же легко прослеживается зависимость времени выполнения тикета от его приоритета.
df.groupby(['Priority'])['Resolution_time'].describe()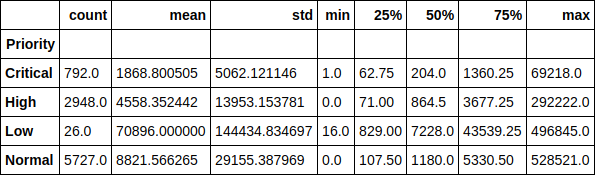
Или вот в качестве графика медианное значение. Как видно, картина особо не поменялась, следовательно, выбросы не очень влияют на распределение.
df.groupby(['Priority'])['Resolution_time'].median().sort_values().plot(kind='bar', figsize=(12,7), rot=0, fontsize=14);
Теперь посмотрим на среднее время решения тикета по каждому из инженеров в зависимости от того, сколько тикетов в работе было на тот момент у этого инженера. На самом деле эти графики, к моему удивлению, не показывают какой-то единой картины. У некоторых время выполнения увеличивается по мере увеличения текущих тикетов в работе, а у некоторые эта зависимость обратная. У некоторых же зависимость и вовсе не прослеживается.
Однако, снова забегая вперед, скажу, что наличие этого признака в датасете повысило точность модели более чем в 2 раза и влияние на время выполнения однозначно есть. Просто мы его не видим. А модель видит.
engineers = [i.replace('_vacation', '') for i in df.columns if 'vacation' in i]
cols = 2
rows = int(len(engineers) / cols)
fig, axes = plt.subplots(nrows=rows, ncols=cols, figsize=(16,24))
for i in range(rows):
for j in range(cols):
df.groupby(engineers[i * cols + j])['Resolution_time'].mean().plot(kind='bar', rot=0, ax=axes[i, j]).set_xlabel('Engineer_' + str(i * cols + j + 1))
del cols, rows, fig, axes
Сделаем небольшую матрицу попарного взаимодействия следующих признаков: время решения тикета, количество голосов и количество наблюдателей. Бонусом по диагонали у нас распределение каждого признака.
Из интересного — видна зависимость снижения времени решения тикета от растущего количества наблюдателей. Так же видно, что голосами люди пользуются не очень активно.
pd.scatter_matrix(df[['Resolution_time', 'Watchers', 'Votes']], figsize=(15, 15), diagonal='hist');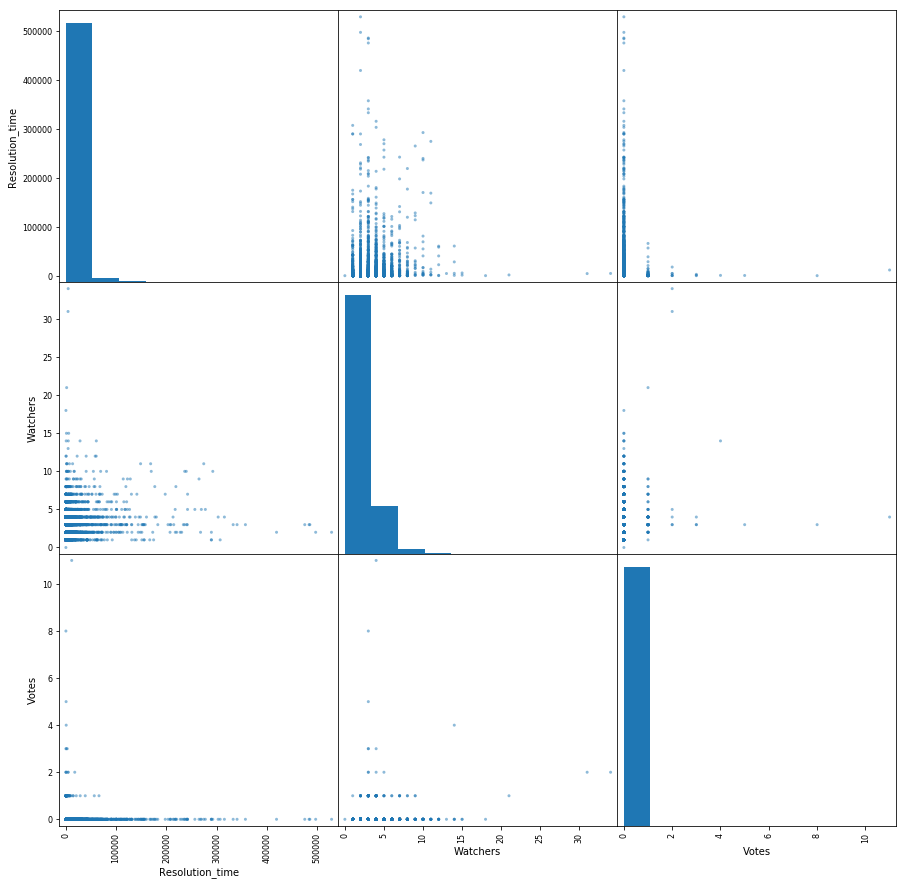
Итак, мы провели небольшой предварительный анализ данных, увидели существующие зависимости между целевым признаком, коим является время решения тикета, и такими признаками как количество голосов за тикет, количество "наблюдателей" за ним и его приоритет. Двигаемся дальше.
Построение модели. Выстраиваем признаки
Настала пора переходить к построению самой модели. Но для начала нам нужно привести наши признаки в понятный для модели вид. Т.е. разложить категориальные признаки на разреженные вектора и избавиться от лишнего. Например, поля со временем создания и закрытия тикета нам не понадобятся в модели, равно как и поле Assignee, т.к. мы будем в итоге использовать эту модель для предсказания времени выполнения тикета, который еще ни на кого не назначен ("заассайнен").
Целевым признаком, как я только что упоминал, для нас является время решения проблемы, поэтому забираем его в качестве отдельного вектора и тоже удаляем из общего набора данных. Кроме того, некоторые поля у нас оказались пустыми ввиду того, что не всегда репортеры заполняют поле описания при оформлении тикета. В таком случае pandas выставляет их значения в NaN, мы же просто заменим их на пустую строку.
y = df['Resolution_time']
df.drop(['Created', 'Resolved', 'Resolution_time', 'Assignee'], axis=1, inplace=True)
df['Description'].fillna('', inplace=True)
df['Summary'].fillna('', inplace=True)Раскладываем категориальные признаки на разреженные вектора (One-hot encoding). Пока не трогаем поля с описанием и оглавлением тикета. Их мы будем использовать несколько иначе. Некоторые имена репортеров содержат знак [X]. Так JIRA помечает неактивных сотрудников, которые больше не работают в компании. Я решил оставить их среди признаков, хотя можно и очистить от них данные, поскольку в будущем, при использовании модели, мы уже не встретим тикетов от этих сотрудников.
def create_df(dic, feature_list):
out = pd.DataFrame(dic)
out = pd.concat([out, pd.get_dummies(out[feature_list])], axis = 1)
out.drop(feature_list, axis = 1, inplace = True)
return out
X = create_df(df, df.columns[df.dtypes == 'object'].drop(['Description', 'Summary']))
X.columns = X.columns.str.replace(' \[X\]', '')А вот теперь займемся полем описания в тикете. Работать с ним мы будем одним из, пожалуй, самых простых способов — соберем все использованные в наших тикетах слова, посчитаем среди них самые популярные, отбросим "лишние" слова — те, которые очевидно не могут влиять на результат, как, к примеру, слово "пожалуйста" (please — всё общение в JIRA у нас происходит строго на английском языке), являющееся самым популярным. Да, вот такие у нас вежливые люди.
Так же уберем "стоп-слова", согласно библиотеке nltk, и более тщательно очистим текст от лишних символов. Напомню, что это самое простое, что можно сделать с текстом. Мы не проводим "стемминг" слов, так же можно посчитать самые популярные N-граммы слов, но мы ограничимся лишь этим.
all_words = np.concatenate(df['Description'].apply(lambda s: s.split()).values)
stop_words = stopwords.words('english')
stop_words.extend(['please', 'hi', '-', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '(', ')', '=', '{', '}'])
stop_words.extend(['h3', '+', '-', '@', '!', '#', '$', '%', '^', '&', '*', '(for', 'output)'])
stop_symbols = ['=>', '|', '[', ']', '#', '*', '\\', '/', '->', '>', '<', '&']
words_series = pd.Series(list(all_words))
del all_words
words_series = words_series[~words_series.isin(stop_words)]
for symbol in stop_symbols:
words_series = words_series[~words_series.str.contains(symbol, regex=False, na=False)]После всего этого у нас на выходе получился объект pandas.Series, содержащий все использованные слова. Давайте посмотрим на самые популярные из них и возьмем первые 50 из списка, чтобы использовать в качестве признаков. Для каждого из тикетов мы будем смотреть употребляется ли это слово в описании, и если да, то в соответствующей ему колонке ставить 1, в противном случае 0.
usefull_words = list(words_series.value_counts().head(50).index)
print(usefull_words[0:10])['error', 'account', 'info', 'call', '{code}', 'behavior', 'array', 'update', 'env', 'actual']Теперь в нашем общем наборе данных создадим для выбранных нами слов отдельные колонки. На этом от самого поля описания можно избавиться.
for word in usefull_words:
X['Description_' + word] = X['Description'].str.contains(word).astype('int64')
X.drop('Description', axis=1, inplace=True)Сделаем то же самое и для поля заголовка тикета.
all_words = np.concatenate(df['Summary'].apply(lambda s: s.split()).values)
words_series = pd.Series(list(all_words))
del all_words
words_series = words_series[~words_series.isin(stop_words)]
for symbol in stop_symbols:
words_series = words_series[~words_series.str.contains(symbol, regex=False, na=False)]
usefull_words = list(words_series.value_counts().head(50).index)
for word in usefull_words:
X['Summary_' + word] = X['Summary'].str.contains(word).astype('int64')
X.drop('Summary', axis=1, inplace=True)Посмотрим, что в итоге у нас получилось в матрице признаков X и векторе ответов y.
print(X.shape, y.shape)((9493, 1114), (9493,))Теперь разделим эти данные на тренировочную (обучающую) выборку и тестовую выборку в процентном соотношении 75/25. Итого имеем 7119 примеров, на которых будем тренироваться, и 2374, по которым будем оценивать наши модели. А размерность нашей матрицы признаков увеличилась до 1114 за счет раскладывания категориальных признаков.
X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.25, random_state=17)
print(X_train.shape, X_holdout.shape)((7119, 1114), (2374, 1114))Тренируем модель.
Линейная регрессия
Начнем с самой легкой и (ожидаемо) наименее точной модели — линейной регрессии. Оценивать будем как по точности на тренировочных данных, так и по отложенной (holdout) выборке — данным, которые модель не видела.
В случае с линейной регрессией модель более-менее приемлемо показывает себя на тренировочных данных, но вот точность на отложенной выборке чудовищно низкая. Даже намного хуже, чем предсказывать по обычному среднему значению по всем тикетам.
Здесь нужно сделать небольшую паузу и рассказать, как модель оценивает качество с помощью своего метода score.
Оценка производится по коэффициенту детерминации:
Где — результат, предсказанный моделью а
— среднее значение по всей выборке.
Мы сейчас слишком подробно на коэффициенте останавливаться не будем. Отметим лишь, что он не во всей мере отражает ту точность модели, которая нас интересует. Поэтому одновременно мы будем использовать для оценки Среднюю Абсолютную Ошибку (Mean Absolute Error — MAE) и опираться будем именно на неё.
lr = LinearRegression()
lr.fit(X_train, y_train)
print('R^2 train:', lr.score(X_train, y_train))
print('R^2 test:', lr.score(X_holdout, y_holdout))
print('MAE train', mean_absolute_error(lr.predict(X_train), y_train))
print('MAE test', mean_absolute_error(lr.predict(X_holdout), y_holdout))R^2 train: 0.3884389470220214
R^2 test: -6.652435243123196e+17
MAE train: 8503.67256637168
MAE test: 1710257520060.8154Градиентный бустинг
Ну куда же без него, без градиентного бустинга? Давайте попробуем натренировать модель и посмотрим, что у нас получится. Использовать для этого будем небезызвестный XGBoost. Начнем со стандартных настроек гиперпараметров.
import xgboost
xgb = xgboost.XGBRegressor()
xgb.fit(X_train, y_train)
print('R^2 train:', xgb.score(X_train, y_train))
print('R^2 test:', xgb.score(X_holdout, y_holdout))
print('MAE train', mean_absolute_error(xgb.predict(X_train), y_train))
print('MAE test', mean_absolute_error(xgb.predict(X_holdout), y_holdout))R^2 train: 0.5138516547636054
R^2 test: 0.12965507684512545
MAE train: 7108.165167471887
MAE test: 8343.433260957032Результат из коробки уже не плохой. Попробуем потюнинговать модель, подбирая гиперпараметры: n_estimators, learning_rate и max_depth. В итоге остановимся на значениях в 150, 0.1 и 3 соответственно, как показывающих наилучший результат на тестовой выборке при отсутствии перетренированности модели на тренировочных данных.
*Вместо R^2 Score на картинке должна быть MAE.
xgb_model_abs_testing = list()
xgb_model_abs_training = list()
rng = np.arange(1,151)
for i in rng:
xgb = xgboost.XGBRegressor(n_estimators=i)
xgb.fit(X_train, y_train)
xgb.score(X_holdout, y_holdout)
xgb_model_abs_testing.append(mean_absolute_error(xgb.predict(X_holdout), y_holdout))
xgb_model_abs_training.append(mean_absolute_error(xgb.predict(X_train), y_train))
plt.figure(figsize=(14, 8))
plt.plot(rng, xgb_model_abs_testing, label='MAE test');
plt.plot(rng, xgb_model_abs_training, label='MAE train');
plt.xlabel('Number of estimators')
plt.ylabel('$R^2 Score$')
plt.legend(loc='best')
plt.show();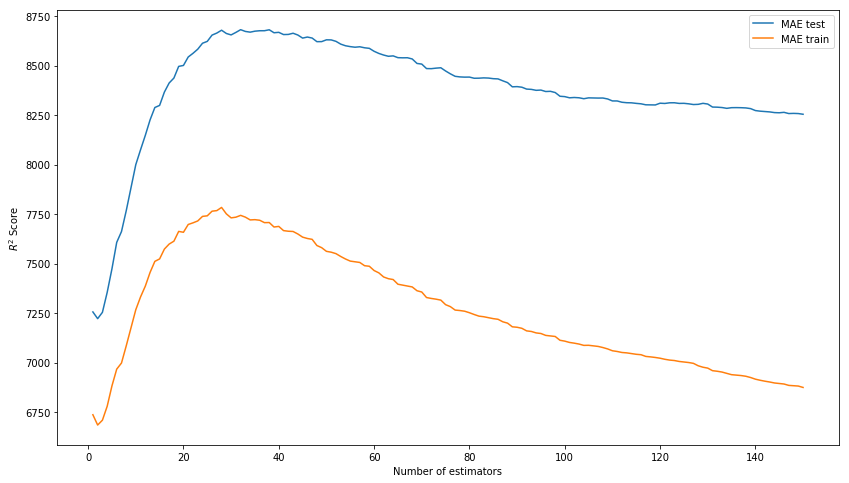
xgb_model_abs_testing = list()
xgb_model_abs_training = list()
rng = np.arange(0.05, 0.65, 0.05)
for i in rng:
xgb = xgboost.XGBRegressor(n_estimators=150, random_state=17, learning_rate=i)
xgb.fit(X_train, y_train)
xgb.score(X_holdout, y_holdout)
xgb_model_abs_testing.append(mean_absolute_error(xgb.predict(X_holdout), y_holdout))
xgb_model_abs_training.append(mean_absolute_error(xgb.predict(X_train), y_train))
plt.figure(figsize=(14, 8))
plt.plot(rng, xgb_model_abs_testing, label='MAE test');
plt.plot(rng, xgb_model_abs_training, label='MAE train');
plt.xlabel('Learning rate')
plt.ylabel('MAE')
plt.legend(loc='best')
plt.show();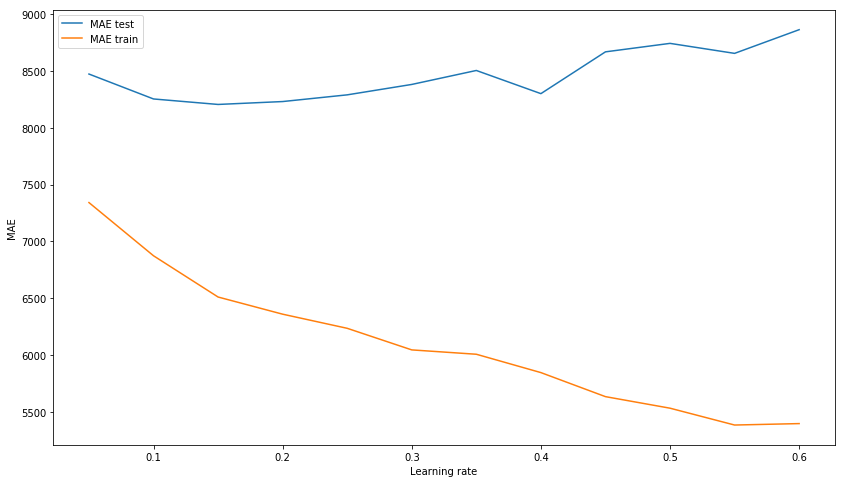
xgb_model_abs_testing = list()
xgb_model_abs_training = list()
rng = np.arange(1, 11)
for i in rng:
xgb = xgboost.XGBRegressor(n_estimators=150, random_state=17, learning_rate=0.1, max_depth=i)
xgb.fit(X_train, y_train)
xgb.score(X_holdout, y_holdout)
xgb_model_abs_testing.append(mean_absolute_error(xgb.predict(X_holdout), y_holdout))
xgb_model_abs_training.append(mean_absolute_error(xgb.predict(X_train), y_train))
plt.figure(figsize=(14, 8))
plt.plot(rng, xgb_model_abs_testing, label='MAE test');
plt.plot(rng, xgb_model_abs_training, label='MAE train');
plt.xlabel('Maximum depth')
plt.ylabel('MAE')
plt.legend(loc='best')
plt.show();
Теперь обучим модель с подобранными гиперпараметрами.
xgb = xgboost.XGBRegressor(n_estimators=150, random_state=17, learning_rate=0.1, max_depth=3)
xgb.fit(X_train, y_train)
print('R^2 train:', xgb.score(X_train, y_train))
print('R^2 test:', xgb.score(X_holdout, y_holdout))
print('MAE train', mean_absolute_error(xgb.predict(X_train), y_train))
print('MAE test', mean_absolute_error(xgb.predict(X_holdout), y_holdout))R^2 train: 0.6745967150462303
R^2 test: 0.15415143189670344
MAE train: 6328.384400466232
MAE test: 8217.07897417256Итоговый результат с выбранными параметрами и визуализация feature importance — важность признаков по мнению модели. На первом месте количество наблюдателей за тикетом, а вот затем идут сразу 4 инженера. Соответственно на время решения тикета довольно сильно может повлиять занятость того или иного инженера. И вполне логично, что свободное время некоторых из них важнее. Хотя бы потому, что в команде есть как senior инженеры, так и middle (junior'ов у нас в команде нет). Кстати, снова по секрету, инженер, стоящий на первом месте (оранжевый столбик) действительно один из самых опытных среди всей команды. Более того — все 4 этих инженера имеют приставку senior в своей должности. Получается, что модель это лишний раз подтвердила.
features_df = pd.DataFrame(data=xgb.feature_importances_.reshape(1, -1), columns=X.columns).sort_values(axis=1, by=[0], ascending=False)
features_df.loc[0][0:10].plot(kind='bar', figsize=(16, 8), rot=75, fontsize=14);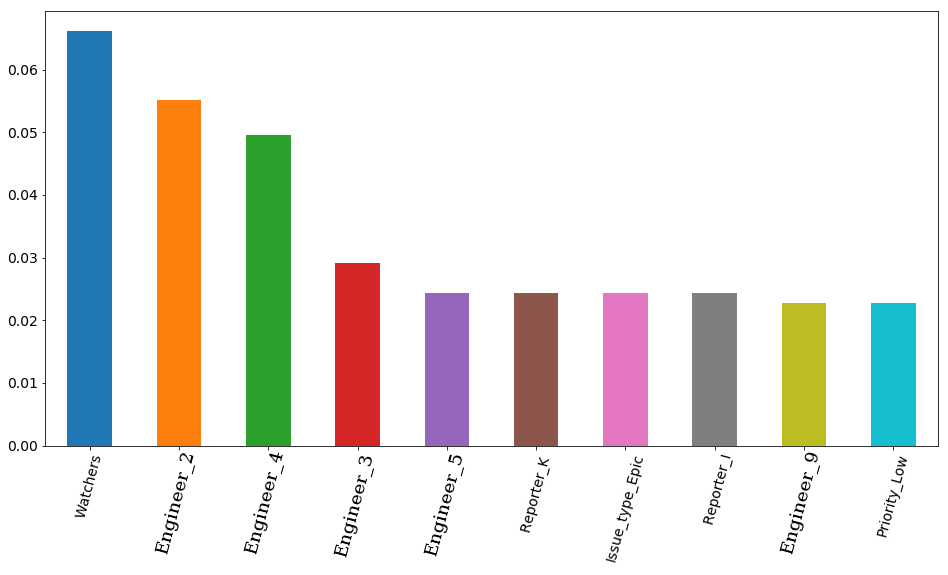
Нейронная сеть
Но на одном градиентном бустинге останавливаться не станем и попробуем натренировать нейросеть, а точнее Многослойный перцептрон (Multilayer perceptron), полносвязную нейронную сеть прямого распространения. На сей раз не будем начинать со стандартных настроек гиперпараметров, т.к. в библиотеке sklearn, которую мы будем использовать, по умолчанию только один скрытый слой со 100 нейронами и при тренировке модель выдает предупреждение о несхождении за стандартные 200 итераций. Мы же используем сразу 3 скрытых слоя с 300, 200 и 100 нейронами соответственно.
В результате мы видим, что модель неслабо перетренировывается на обучающей выборке, что, впрочем, не мешает ей показывать достойный результат на тестовой выборке. Этот результат совсем чуть-чуть уступает результату градиентного бустинга.
from sklearn.neural_network import MLPRegressor
nn = MLPRegressor(random_state=17, hidden_layer_sizes=(300, 200 ,100), alpha=0.03,
learning_rate='adaptive', learning_rate_init=0.0005, max_iter=200, momentum=0.9,
nesterovs_momentum=True)
nn.fit(X_train, y_train)
print('R^2 train:', nn.score(X_train, y_train))
print('R^2 test:', nn.score(X_holdout, y_holdout))
print('MAE train', mean_absolute_error(nn.predict(X_train), y_train))
print('MAE test', mean_absolute_error(nn.predict(X_holdout), y_holdout))R^2 train: 0.9771443840549647
R^2 test: -0.15166596239118246
MAE train: 1627.3212161350423
MAE test: 8816.204561947616Посмотрим, чего мы сможем добиться попытками подобрать наилучшую архитектуру нашей сети. Для начала натренируем несколько моделей с одним скрытым слоем и одну с двумя, просто чтобы лишний раз убедиться, что модели с одним слоем не успевают сойтись за 200 итераций и, как видно по графику, сходиться могут очень и очень долго. Добавление еще одного слоя уже неплохо помогает.
plt.figure(figsize=(14, 8))
for i in [(500,), (750,), (1000,), (500,500)]:
nn = MLPRegressor(random_state=17, hidden_layer_sizes=i, alpha=0.03,
learning_rate='adaptive', learning_rate_init=0.0005, max_iter=200, momentum=0.9,
nesterovs_momentum=True)
nn.fit(X_train, y_train)
plt.plot(nn.loss_curve_, label=str(i));
plt.xlabel('Iterations')
plt.ylabel('MSE')
plt.legend(loc='best')
plt.show()
А теперь потренируем побольше моделей с совершенно различной архитектурой. От 3 скрытых слоёв до 10 и посмотрим какая из них покажет себя лучше.
plt.figure(figsize=(14, 8))
for i in [(500,300,100), (80, 60, 60, 60, 40, 40, 40, 40, 20, 10), (80, 60, 60, 40, 40, 40, 20, 10),
(150, 100, 80, 60, 40, 40, 20, 10), (200, 100, 100, 100, 80, 80, 80, 40, 20), (80, 40, 20, 20, 10, 5),
(300, 250, 200, 100, 80, 80, 80, 40, 20)]:
nn = MLPRegressor(random_state=17, hidden_layer_sizes=i, alpha=0.03,
learning_rate='adaptive', learning_rate_init=0.001, max_iter=200, momentum=0.9,
nesterovs_momentum=True)
nn.fit(X_train, y_train)
plt.plot(nn.loss_curve_, label=str(i));
plt.xlabel('Iterations')
plt.ylabel('MSE')
plt.legend(loc='best')
plt.show()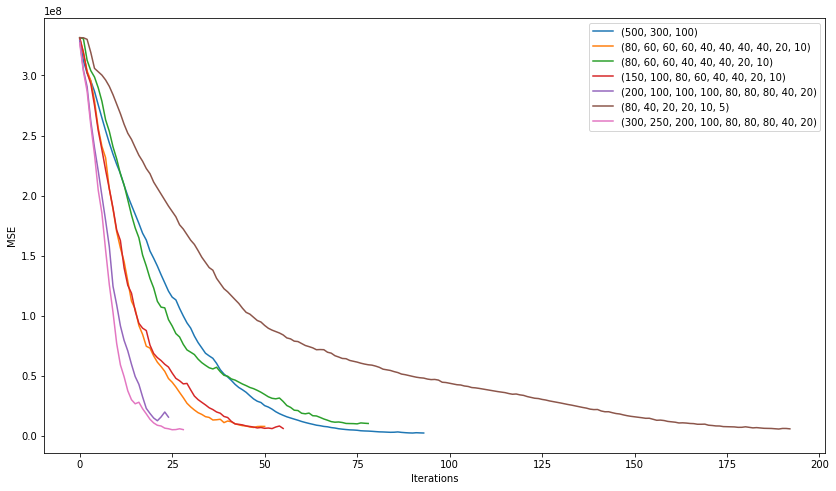
Победила в этом "соревновании" модель с архитектурой (200, 100, 100, 100, 80, 80, 80, 40, 20) показавшая следующую среднюю ошибку:
2506 на обучающей выборке
7351 на тестовой выборке
Результат оказался лучше, чем у градиентного бустинга, хоть и наталкивает на мысль о переобучении модели. Попробуем немного увеличить регуляризацию и learning rate и посмотреть на результат.
nn = MLPRegressor(random_state=17, hidden_layer_sizes=(200, 100, 100, 100, 80, 80, 80, 40, 20), alpha=0.1,
learning_rate='adaptive', learning_rate_init=0.007, max_iter=200, momentum=0.9,
nesterovs_momentum=True)
nn.fit(X_train, y_train)
print('R^2 train:', nn.score(X_train, y_train))
print('R^2 test:', nn.score(X_holdout, y_holdout))
print('MAE train', mean_absolute_error(nn.predict(X_train), y_train))
print('MAE test', mean_absolute_error(nn.predict(X_holdout), y_holdout))R^2 train: 0.836204705204337
R^2 test: 0.15858607391959356
MAE train: 4075.8553476632796
MAE test: 7530.502826043687Ну вот, стало получше. Средняя ошибка на обучающей выборке увеличилась, но ошибка на тестовой выборке практически не изменилась. Это позволяет предположить, что такая модель лучше генерализуется на данных, которые она не видела.
Теперь попробуем вывести важность признаков. Сделаем это следующим образом: возьмем абсолютный вес для каждого из признаков по каждому из нейронов в первом из скрытых слоёв (это тот, в котором 200 нейронов). И посчитаем, какие из признаков имеют наибольший вес по "мнению" наибольшего количества нейронов. К примеру, 30 нейронов из 200 считают, что признак issue type: Epic больше всего влияет на время выполнения тикета. Причем здесь мы не видим в какую именно сторону, т.к. берем абсолютное значение веса, но если подумать, то этот тип тикета используется довольно редко и в основном работы по нему занимают продолжительное время, так что не сложно предположить, что этот признак влияет на время решения в сторону его увеличения. А вот на 4 и 5 местах расположился приоритет тикета. И если низкий приоритет также влияет на увеличение времени, то критический его уменьшает. Эту зависимость мы с вами проследили самостоятельно еще в самом начале, а теперь её выявила и модель.
Однако здесь стоит сделать небольшую ремарку — поскольку в нашей модели аж 9 скрытых слоёв, то определять важность признаков по весам только первого из них не совсем корректно. По этой картинке приятно посмотреть, что модель по крайней мере ведет себя адекватно относительно важности признаков, но чем глубже в сеть будут уходить данные, тем сложнее в удобопонимаемом для человека виде их будет представить.
pd.Series([X_train.columns[abs(nn.coefs_[0][:,i]).argmax()] for i in range(nn.hidden_layer_sizes[0])]).value_counts().head(5).sort_values().plot(kind='barh', title='Feature importance', fontsize=14, figsize=(14,8));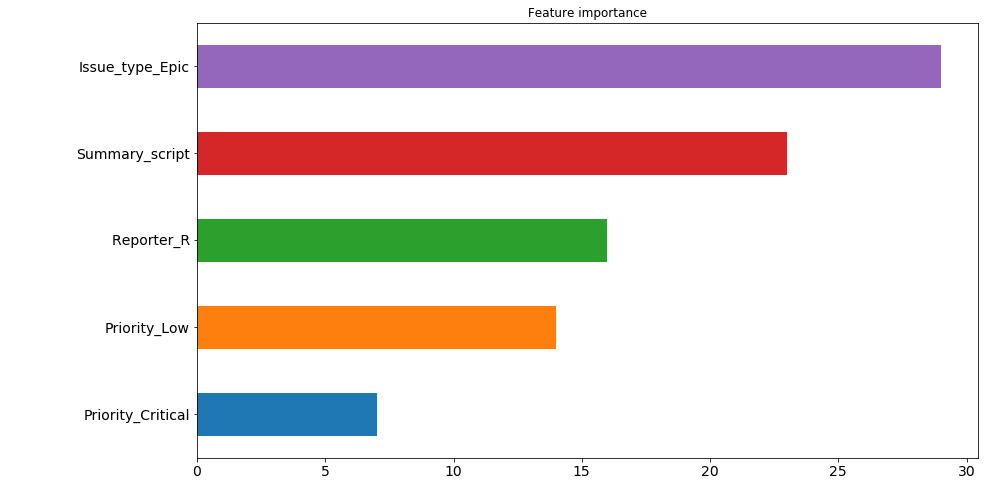
Ансамбль моделей
А в этой части сделаем ансамбль из двух моделей методом усреднения их предсказаний. Зачем? Вроде бы вот ошибка одной модели 7530 а другой 8217. Ведь усреднение должно равняться (7530 + 8217) / 2 = 7873, что хуже, чем ошибка нейронной сети, так? Нет, не так. Мы усредняем не ошибку, а предсказания моделей. И ошибка от этого взяла, да и уменьшилась до 7526.
Вообще ансамбль моделей довольно мощная вещь, люди так соревнования на kaggle выигрывают. А ведь представленный метод усреднения, пожалуй, самый простой из них.
nn_predict = nn.predict(X_holdout)
xgb_predict = xgb.predict(X_holdout)
print('NN MSE:', mean_squared_error(nn_predict, y_holdout))
print('XGB MSE:', mean_squared_error(xgb_predict, y_holdout))
print('Ensemble:', mean_squared_error((nn_predict + xgb_predict) / 2, y_holdout))
print('NN MAE:', mean_absolute_error(nn_predict, y_holdout))
print('XGB MSE:', mean_absolute_error(xgb_predict, y_holdout))
print('Ensemble:', mean_absolute_error((nn_predict + xgb_predict) / 2, y_holdout))NN MSE: 628107316.262393
XGB MSE: 631417733.4224195
Ensemble: 593516226.8298339
NN MAE: 7530.502826043687
XGB MSE: 8217.07897417256
Ensemble: 7526.763569558157Анализ результатов
Итого что мы имеем на данный момент? Наша модель ошибается примерно на 7500 минут в среднем. Т.е. на 5 с небольшим дней. Выглядит как не очень точное предсказание для времени выполнения тикета. Но расстраиваться и паниковать рано. Давайте посмотрим, где именно модель ошибается больше всего и на сколько.
Список с максимальными ошибками модели (в минутах):
((nn_predict + xgb_predict) / 2 - y_holdout).apply(np.abs).sort_values(ascending=False).head(10).values[469132.30504392, 454064.03521379, 252946.87342439, 251786.22682697, 224012.59016987, 15671.21520735, 13201.12440327, 203548.46460229, 172427.32150665, 171088.75543224]Числа внушительные. Посмотрим, что это за тикеты.
df.loc[((nn_predict + xgb_predict) / 2 - y_holdout).apply(np.abs).sort_values(ascending=False).head(10).index][['Issue_type', 'Priority', 'Worktype', 'Summary', 'Watchers']]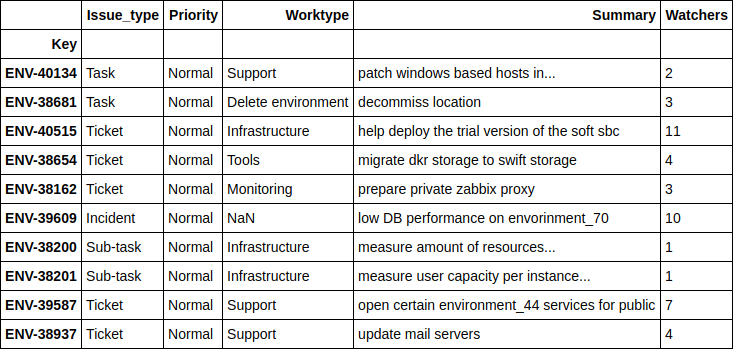
Не буду слишком сильно вдаваться в подробности по каждому из тикетов, но в целом видно что это какие-то глобальные проекты, по которым даже человек не сможет спрогнозировать точных сроков завершения. Скажу лишь что целых 4 тикета здесь связаны с переездом оборудования из одной локации в другую.
А теперь давайте взглянем, где наша модель показывает самые точные результаты.
print(((nn_predict + xgb_predict) / 2 - y_holdout).apply(np.abs).sort_values().head(10).values)
df.loc[((nn_predict + xgb_predict) / 2 - y_holdout).apply(np.abs).sort_values().head(10).index][['Issue_type', 'Priority', 'Worktype', 'Summary', 'Watchers']][ 1.24606014, 2.6723969, 4.51969139, 10.04159236, 11.14335444, 14.4951508, 16.51012874, 17.78445744, 21.56106258, 24.78219295]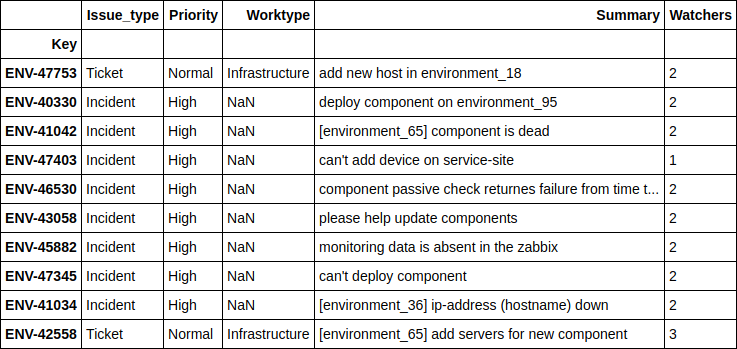
Видно, что лучше всего модель предсказывает случаи, когда люди просят развернуть какой-то дополнительный сервер на их окружении, либо когда происходят какие-то мелкие ошибки на уже существующих окружениях и сервисах. И, как правило, больше всего для репортера важно иметь примерное время решения именно таких проблем, с чем модель отлично справляется.
Как поле Engineer увеличило точность
Помните, я несколько раз обещал рассказать о полях 'Engineer', содержащих количество открытых тикетов, находящихся в работе, на каждом из инженеров на момент поступления нового тикета? Сдерживаю обещание.
Дело в том, что до добавления этих данных точность модели была хуже текущей примерно в 2 раза. Я, конечно, пробовал различные оптимизации гиперпараметров, пробовал делать более хитрый ансамбль из моделей, но всё это повышало точность совсем незначительно. В итоге, немного поразмыслив, и воспользовавшись тем, что я знаю всю "кухню" работы нашего отдела изнутри, был сделан вывод что не только (и не столько) приоритет, тип тикета и любые другие его поля имеют важность, влияющую на время его решения, как занятость инженеров. Согласитесь, если все сотрудники отдела завалены работой и сидят "в мыле", то никакое выставление приоритетов и изменение описания проблемы не поможет ускорить процесс его решения.
Идея мне показалась здравой, и я решил собрать нужную информацию. Подумав самостоятельно и посоветовавшись с коллегами, я не нашел ничего другого, кроме как проходить циклом по всем уже собранным тикетам и для каждого из них запускать внутренний цикл по каждому из 12 инженеров, делая запрос следующего вида (это язык JQL использующийся в JIRA):
assignee was engineer_N during (ticket_creation_date) and status was "In Progress"В результате получилось 10783 * 12 = 129396 запросов, которые заняли… неделю. Да, на то, чтобы достать такие исторические данные по каждому из тикетов для каждого из инженеров ушла ровно календарная неделя, т.е. примерно по 5 секунд на запрос.
Теперь представьте, как я был рад, когда эти новые полученные данные, добавленные в модель, улучшили её точность сразу в 2 раза. Было бы неприятно потратить неделю на сбор данных и в итоге не получить ничего.
Итоги и планы на будущее
Модель с приемлемой точностью предсказывает время решения самых распространенных задач и это уже хорошее подспорье. Теперь она используется в нашей команде для внутреннего SLO на который мы ориентируемся, выстраивая нашу очередь тикетов.
Кроме того, есть идея использовать этот же набор данных для предсказания инженера, который займется новой поступившей задачей (люди в команде специализируются на разных вещах: кто-то больше занимается телефонией, кто-то настраивает мониторинг, а кто-то работает с базами данных) и для поиска похожих тикетов уже решенных ранее, что поможет сократить время на дебаггинг проблемы используя уже имеющийся опыт.