Содержание
Часть 1: Введение.
Часть 2: Аппаратное обеспечение GPU и шаблоны параллельной коммуникации.
Часть 3: Фундаментальные алгоритмы GPU: свертка (reduce), сканирование (scan) и гистограмма (histogram).
Часть 4: Фундаментальные алгоритмы GPU: уплотнение (compact), сегментированное сканирование (segmented scan), сортировка. Практическое применение некоторых алгоритмов.
Часть 5: Оптимизация GPU программ.
Часть 6: Примеры параллелизации последовательных алгоритмов.
Часть 7: Дополнительные темы параллельного программирования, динамический параллелизм.
Шаблоны параллельной коммуникации

Что собой представляют параллельные вычисления? Не что иное, как множество потоков, решающие определенную задачу кооперативно. Ключевое слово здесь «кооперативно» — для достижения кооперации нужно применять определенные механизмы коммуникации между потоками. При использовании CUDA, коммуникация осуществляется через память: потоки могут читать входные данные, изменять выходные данные либо обмениваться «промежуточными» результатами.
В зависимости от того, каким именно образом потоки общаются через память, выделяют различные шаблоны параллельной коммуникации.
В предыдущей части в качестве простого примера использования CUDA была рассмотрена задача конвертации цветного изображения в оттенки серого. Для этого, интенсивность каждого пиксела выходного изображения в оттенках серого рассчитывалась по формуле I=A*pix.R+B*pix.G+C*pix.B, где A, B, C — константы, pix — соответствующий пиксел исходного изображения. Графически этот процесс выглядит следующим образом:

Если абстрагироваться от самого способа расчета выходного значения, получаем первый шаблон параллельной коммуникации — map: над каждым элементом входных данных, с индексом i, выполняется одна и та же функция, а результат сохраняется в выходном массиве данных под тем же индексом i. Шаблон map очень эффективен на GPU, и к тому же просто выражается в рамках CUDA — достаточно запустить по одному потоку на каждый входной элемент (как и было сделано в предыдущей части для задачи конвертации изображения). Однако, лишь малую часть задач можно решить используя только этот шаблон.
Если же для вычисления выходного значения с индексом i используются несколько входных элементов, то такой шаблон называют gather, и выглядеть он может так:

Или так:

Эффективность реализации данного шаблона на CUDA зависит от того, какие именно входные значения используются при расчете выходного и их количества — лучше всего когда используется небольшое количество идущих подряд элементов.
Обратный шаблон, scatter — каждый входной элемент влияет на несколько (либо один) выходных элементов, графически выглядит так же как и gather, однако меняется смысл: теперь мы «отталкиваемся» не от выходных элементов, для которых рассчитываем их значение, а от входных, которые влияют на значения определенных выходных элементов. Довольно часто одна и та же задача может быть решена в рамках как шаблона gather, так и scatter. Например, если мы хотим усреднить 3 соседних входных элемента и записать их в выходной массив, то можно:
- запустить по потоку на каждый выходной элемент, где каждый поток будет усреднять значения 3 соседних входных элементов — gather;
- либо запустить по потоку на каждый входной элемент, где каждый поток будет добавлять 1/3 значения своего входного элемента к значению соответствующего выходного элемента — scatter.
Как вы скорее всего догадались, при использовании подхода scatter встает проблема синхронизации, так как несколько потоков могут пытаться модифицировать один и тот же выходной элемент одновременно.
Также стоит выделить подвид шаблона gather — stencil: в данном шаблоне накладывается ограничение на входные элементы, которые участвуют в вычислении выходного элемента — а именно, это могут быть только соседние элементы. В случае с 2D/3D изображениями, могут использоваться различные виды данного шаблона, например двумерный трафарет фон Неймана:

или двумерный трафарет Мура:

В связи с этим ограничением, шаблон stencil обычно довольно эффективно реализуется в рамках CUDA: достаточно запустить по одному потоку на каждый выходной элемент, при этом поток будет считывать нужные ему входные элементы. При такой организации вычислений, эффективность обеспечивается двумя факторами:
- Все данные, нужные для одного потока, сгруппированы в памяти (в случае одномерного массива — сплошной «кусок» памяти, в 2D случае — несколько кусков памяти, находящихся на одинаковом расстоянии друг от друга).
- Значение некоторого входного элемента считывается несколько раз из соседних потоков (конкретное количество считываний зависит от выбранной маски) — появляется возможность «переиспользовать» данные, предоставляемая нам CUDA — об этом будет рассказано дальше в статье.
Аппаратное обеспечение GPU
Рассмотрим высокоуровневую структуру аппаратного обеспечения GPU:
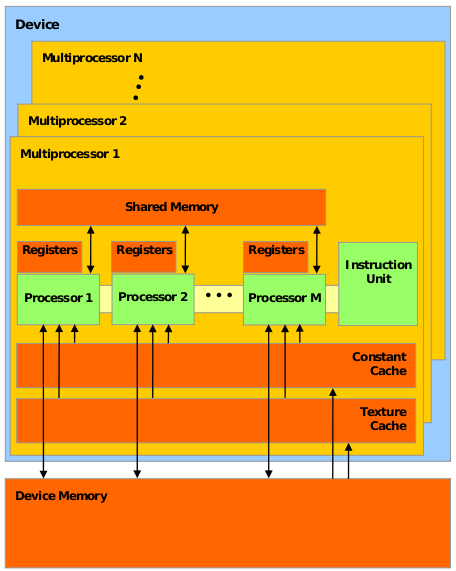
- CUDA-совместимый GPU состоит из нескольких (обычно десятков) streaming multiprocessors (потоковых мультипроцессоров), далее SM.
- Каждый SM, в свою очередь, состоит из нескольких десятков simple/streaming processors (SP) (обычных/потоковых процессоров), или выражаясь более точно, CUDA cores (ядер CUDA). Эти ребята уже больше похожи на привычный CPU — имеют свои регистры, кэш и т.д. Каждый SM также имеет свою собственную shared memory (общую память) — эдакий дополнительный кэш, который доступен всем SP, и может использоваться как в роли кэша для часто используемых данных, так и для «общения» между потоками одного блока CUDA.
- GPU имеет и свою собственную память, называемую device memory, общую для всех потоков CUDA — именно с ней работают функции cudaMalloc и cudaMemcpy
(также ее размером очень любят меряться школьники и производители GPU).
Соответствие модели CUDA и аппаратного обеспечения GPU. Гарантии CUDA
Согласно модели CUDA, программист разбивает задачу на блоки, а блоки на потоки. Каким же образом выполняется сопоставление этих программных сущностей с выше описанными аппаратными блоками GPU?

- Каждый блок будет полностью выполнен на выделенном ему SM.
- Распределением блоков по SM занимается GPU, не программист.
- Все потоки блока X будут разбиты на группы, называемые warps (обычно так и говорят — варпы), и выполнены на SM. Размер этих групп зависит от модели GPU, например для моделей с микроархитектурой Fermi он равен 32. Все потоки из одного варпа выполняются одновременно, занимая определенную часть ресурсов SM. Причем они либо выполняют одну и ту же инструкцию (но на разных данных), либо простаивают.
Исходя из всего этого, CUDA предоставляет следующие гарантии:
- Все потоки в определенном блоке будут выполнены на каком-то одном SM.
- Все потоки определенного ядра будут выполнены до начала выполнения следующего ядра.
CUDA не гарантирует что:
- Какой-то блок X будет выполнятся до/после/одновременно с каким-то блоком Y.
- Какой-то блок X будет выполнен на каком-то конкретном SM Z.
Синхронизация
Итак, перечислим основные механизмы синхронизации, предоставляемые CUDA:
- Барьер — точка в коде ядра, по достижению которой поток может «пройти» дальше, только если все потоки из его блока достигли этой точки. Еще раз: барьер позволяет синхронизировать только потоки одного блока, а не все потоки в принципе! Ограничение довольно естественное, ведь количество блоков, заданное программистом, может значительно превышать количество доступных SM.
- Атомарные операции — аналогичны атомарным операциям CPU, полный список доступных операций можно посмотреть тут.
- __threadfence — не совсем примитив синхронизации: при достижении этой инструкции поток может продолжить выполнение только после того, как все его манипуляции с памятью станут видны другим потокам — по-сути, заставляет поток выполнить flush кэша.
Основные принципы эффективного использования CUDA
- Принцип увеличение соотношения (время полезной работы) / (время операций с памятью) — обсуждался в предыдущей статье. Значение дроби можно увеличить двумя способами — увеличить числитель, уменьшить знаменатель: то-есть нужно либо делать больше работы, либо тратить меньше времени на операции с памятью. Кроме очевидного решения — по возможности уменьшить количество обращений к памяти, используют следующие принципы эффективной работы с памятью:
- Перемещение часто используемых данных в более быструю память: локальная память потока > общая память блока >> общая память устройства >> память хоста. Таким образом, если в одном блоке несколько потоков используют одни и те же данные — скорее всего есть смысл переместить их в общую память блока.
- Последовательный доступ к памяти: так как потоки в блоках на самом деле выполняются в группах-варпах, то при условии, что потоки в одном варпе будут работать с данными, расположенными в памяти последовательно, CUDA сможет считать один большой кусок памяти за одну инструкцию. В противном же случае — если потоки в варпе будут обращаться к данным, разбросанным в памяти, количество обращений к памяти возрастает.
- Уменьшения расхождения потоков: особенность работы CUDA такова, что потоки в одном варпе всегда либо выполняют одну и ту же инструкцию, либо простаивают. Таким образом, если в коде ядра есть код вида
if (threadIdx.x % 2 == 0) { ... } ...
, то половина потоков варпа (те, которые с нечетным индексом) будут ждать, пока вторая половина выполнит код, находящийся внутри if-а. Поэтому следует избегать таких ситуаций.
Пишем вторую программу на CUDA
Переходим к практике. В качестве примера, иллюстрирующего изложенную теорию, напишем программу, выполняющую размытие изображения по Гауссу. Принцип работы следующий: значение каналов R, G, B пиксела в выходном размытом изображении рассчитывается как взвешенная сумма значений каналов R, G, B (соответственно) всех пикселов исходного изображения в некотором трафарете:

Значения весов рассчитываются используя 2D распределение Гаусса, но как именно это делается не слишком важно для нашей задачи.
Как можно увидеть из описания задачи, для реализации данного алгоритма вполне естественно выбрать шаблон stencil — ведь каждый пиксел выходного изображения рассчитывается исходя из соответствующих соседних пикселей исходного изображения.
Начнем со скелета программы:
main.cpp
#include <chrono>
#include <iostream>
#include <cstring>
#include <string>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/opencv.hpp>
#include <vector_types.h>
#include "openMP.hpp"
#include "CUDA_wrappers.hpp"
#include "common/image_helpers.hpp"
void prepareFilter(float **filter, int *filterWidth, float *filterSigma)
{
static const int blurFilterWidth = 9;
static const float blurFilterSigma = 2.;
*filter = new float[blurFilterWidth * blurFilterWidth];
*filterWidth = blurFilterWidth;
*filterSigma = blurFilterSigma;
float filterSum = 0.f;
const int halfWidth = blurFilterWidth/2;
for (int r = -halfWidth; r <= halfWidth; ++r)
{
for (int c = -halfWidth; c <= halfWidth; ++c)
{
float filterValue = expf( -(float)(c * c + r * r) / (2.f * blurFilterSigma * blurFilterSigma));
(*filter)[(r + halfWidth) * blurFilterWidth + c + halfWidth] = filterValue;
filterSum += filterValue;
}
}
float normalizationFactor = 1.f / filterSum;
for (int r = -halfWidth; r <= halfWidth; ++r)
{
for (int c = -halfWidth; c <= halfWidth; ++c)
{
(*filter)[(r + halfWidth) * blurFilterWidth + c + halfWidth] *= normalizationFactor;
}
}
}
void freeFilter(float *filter)
{
delete[] filter;
}
int main( int argc, char** argv )
{
using namespace cv;
using namespace std;
using namespace std::chrono;
if( argc != 2)
{
cout <<" Usage: blur_image imagefile" << endl;
return -1;
}
Mat image, blurredImage, referenceBlurredImage;
uchar4 *imageArray, *blurredImageArray;
prepareImagePointers(argv[1], image, &imageArray, blurredImage, &blurredImageArray, CV_8UC4);
int numRows = image.rows, numCols = image.cols;
float *filter, filterSigma;
int filterWidth;
prepareFilter(&filter, &filterWidth, &filterSigma);
cv::Size filterSize(filterWidth, filterWidth);
auto start = system_clock::now();
cv::GaussianBlur(image, referenceBlurredImage, filterSize, filterSigma, filterSigma, BORDER_REPLICATE);
auto duration = duration_cast<milliseconds>(system_clock::now() - start);
cout<<"OpenCV time (ms):" << duration.count() << endl;
start = system_clock::now();
BlurImageOpenMP(imageArray, blurredImageArray, numRows, numCols, filter, filterWidth);
duration = duration_cast<milliseconds>(system_clock::now() - start);
cout<<"OpenMP time (ms):" << duration.count() << endl;
cout<<"OpenMP similarity:" << getEuclidianSimilarity(referenceBlurredImage, blurredImage) << endl;
for (int i=0; i<4; ++i)
{
memset(blurredImageArray, 0, sizeof(uchar4)*numRows*numCols);
start = system_clock::now();
BlurImageCUDA(imageArray, blurredImageArray, numRows, numCols, filter, filterWidth);
duration = duration_cast<milliseconds>(system_clock::now() - start);
cout<<"CUDA time full (ms):" << duration.count() << endl;
cout<<"CUDA similarity:" << getEuclidianSimilarity(referenceBlurredImage, blurredImage) << endl;
}
freeFilter(filter);
return 0;
}
По пунктам:
- Читаем файл с изображением, подготавливаем указатели на исходное изображение и результирующее размытое изображение. Функция prepareImagePointers осталась прежней, при необходимости можно посмотреть ее исходный код на bitbucket.
- Подготавливаем фильтр Гаусса — то-есть набор наших весов. Также запоминаем использованные параметры фильтра, чтобы потом передать их в OpenCV и получить образец размытого изображения для проверки корректности работы наших алгоритмов.
- Вызываем функцию размытия по Гауссу из OpenCV, сохраняем полученный образец, замеряем потраченное время.
- Вызываем функцию размытия по Гауссу написанную c использованием OpenMP, замеряем потраченное время, сверяем полученный результат с образцом. Функция вычисления похожести изображений getEuclidianSimilarity выглядит следующим образом:
getEuclidianSimilaritydouble getEuclidianSimilarity(const cv::Mat& a, const cv::Mat& b) { double errorL2 = cv::norm(a, b, cv::NORM_L2); double similarity = errorL2 / (double) (a.rows * a.cols); return similarity; }
По сути, она находит среднюю сумму квадратов разниц значений всех каналов всех пикселей двух изображений. - Вызываем CUDA-вариант размытия по Гауссу 4 раза, каждый раз замеряя потраченное время и сверяя полученный результат с образцом. Зачем вызывать 4 раза? Дело в том, что при самом первом вызове определенное время будет потрачено на инициализацию — поэтому лучше запустить несколько раз и замерять время потраченное на последующих вызовах.
OpenMP реализация алгоритма:
openMP.hpp
#include <stdio.h>
#include <omp.h>
#include <vector_types.h>
#include <vector_functions.h>
void BlurImageOpenMP(const uchar4 * const imageArray,
uchar4 * const blurredImageArray,
const long numRows,
const long numCols,
const float * const filter,
const size_t filterWidth)
{
using namespace std;
const long halfWidth = filterWidth/2;
#pragma omp parallel for collapse(2)
for (long row = 0; row < numRows; ++row)
{
for (long col = 0; col < numCols; ++col)
{
float resR=0.0f, resG=0.0f, resB=0.0f;
for (long filterRow = -halfWidth; filterRow <= halfWidth; ++filterRow)
{
for (long filterCol = -halfWidth; filterCol <= halfWidth; ++filterCol)
{
//Find the global image position for this filter position
//clamp to boundary of the image
const long imageRow = min(max(row + filterRow, static_cast<long>(0)), numRows - 1);
const long imageCol = min(max(col + filterCol, static_cast<long>(0)), numCols - 1);
const uchar4 imagePixel = imageArray[imageRow*numCols+imageCol];
const float filterValue = filter[(filterRow+halfWidth)*filterWidth+filterCol+halfWidth];
resR += imagePixel.x*filterValue;
resG += imagePixel.y*filterValue;
resB += imagePixel.z*filterValue;
}
}
blurredImageArray[row*numCols+col] = make_uchar4(resR, resG, resB, 255);
}
}
}
Для всех 3 каналов каждого пиксела исходного изображения считаем описанную взвешенную сумму, результат записываем в соответствующую позицию выходного изображения.
CUDA вариант:
CUDA.cu
#include <iostream>
#include <cuda.h>
#include "CUDA_wrappers.hpp"
#include "common/CUDA_common.hpp"
__global__
void gaussian_blur(const uchar4* const d_image,
uchar4* const d_blurredImage,
const int numRows,
const int numCols,
const float * const d_filter,
const int filterWidth)
{
const int row = blockIdx.y*blockDim.y+threadIdx.y;
const int col = blockIdx.x*blockDim.x+threadIdx.x;
if (col >= numCols || row >= numRows)
return;
const int halfWidth = filterWidth/2;
extern __shared__ float shared_filter[];
if (threadIdx.y < filterWidth && threadIdx.x < filterWidth)
{
const int filterOff = threadIdx.y*filterWidth+threadIdx.x;
shared_filter[filterOff] = d_filter[filterOff];
}
__syncthreads();
float resR=0.0f, resG=0.0f, resB=0.0f;
for (int filterRow = -halfWidth; filterRow <= halfWidth; ++filterRow)
{
for (int filterCol = -halfWidth; filterCol <= halfWidth; ++filterCol)
{
//Find the global image position for this filter position
//clamp to boundary of the image
const int imageRow = min(max(row + filterRow, 0), numRows - 1);
const int imageCol = min(max(col + filterCol, 0), numCols - 1);
const uchar4 imagePixel = d_image[imageRow*numCols+imageCol];
const float filterValue = shared_filter[(filterRow+halfWidth)*filterWidth+filterCol+halfWidth];
resR += imagePixel.x * filterValue;
resG += imagePixel.y * filterValue;
resB += imagePixel.z * filterValue;
}
}
d_blurredImage[row*numCols+col] = make_uchar4(resR, resG, resB, 255);
}
void BlurImageCUDA(const uchar4 * const h_image,
uchar4 * const h_blurredImage,
const size_t numRows,
const size_t numCols,
const float * const h_filter,
const size_t filterWidth)
{
uchar4 *d_image, *d_blurredImage;
cudaSetDevice(0);
checkCudaErrors(cudaGetLastError());
const size_t numPixels = numRows * numCols;
const size_t imageSize = sizeof(uchar4) * numPixels;
//allocate memory on the device for both input and output
checkCudaErrors(cudaMalloc(&d_image, imageSize));
checkCudaErrors(cudaMalloc(&d_blurredImage, imageSize));
//copy input array to the GPU
checkCudaErrors(cudaMemcpy(d_image, h_image, imageSize, cudaMemcpyHostToDevice));
float *d_filter;
const size_t filterSize = sizeof(float) * filterWidth * filterWidth;
checkCudaErrors(cudaMalloc(&d_filter, filterSize));
checkCudaErrors(cudaMemcpy(d_filter, h_filter, filterSize, cudaMemcpyHostToDevice));
dim3 blockSize;
dim3 gridSize;
int threadNum;
cudaEvent_t start, stop;
cudaEventCreate(&start);
cudaEventCreate(&stop);
threadNum = 32;
blockSize = dim3(threadNum, threadNum, 1);
gridSize = dim3(numCols/threadNum+1, numRows/threadNum+1, 1);
cudaEventRecord(start);
gaussian_blur<<<gridSize, blockSize, filterSize>>>(d_image,
d_blurredImage,
numRows,
numCols,
d_filter,
filterWidth);
cudaEventRecord(stop);
cudaEventSynchronize(stop);
cudaDeviceSynchronize(); checkCudaErrors(cudaGetLastError());
float milliseconds = 0;
cudaEventElapsedTime(&milliseconds, start, stop);
std::cout << "CUDA time kernel (ms): " << milliseconds << std::endl;
checkCudaErrors(cudaMemcpy(h_blurredImage, d_blurredImage, sizeof(uchar4) * numPixels, cudaMemcpyDeviceToHost));
checkCudaErrors(cudaFree(d_filter));
checkCudaErrors(cudaFree(d_image));
checkCudaErrors(cudaFree(d_blurredImage));
}
- Выделяем память на устройстве для исходного изображения, выходного изображения, фильтра. Копируем соответствующие данные с памяти хоста в выделенную память устройства.
- Вызываем ядро. Обратите внимание на новый, 3-й параметр при вызове ядра: <<<gridSize, blockSize, filterSize>>> — он задает размер общей памяти, который необходим каждому блоку. В данной задаче можно было реализовать использование общей памяти блока двумя способами: либо переместить данные фильтра в общую память блока, либо переместить туда «кусок» изображения, который нужен только данному блоку, так как именно эти данные нужны сразу нескольким потокам блока. Однако второй вариант несколько сложнее — нужно учитывать, что кусок входного изображения, который нужен для каждого блока, несколько больше чем сам блок — ведь мы выполняем операцию gather, а значит каждый поток вычисляет значения одного пиксела выходного изображения используя несколько соседних пикселов исходного изображения:
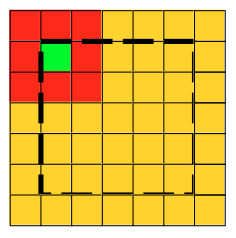
Поэтому я остановился на первом варианте, а значит, каждому блоку нужно ровно sizeof(float)*filterWidth*filterWidth памяти для хранения всех значений фильтра. Перемещение весов фильтра из памяти устройства в общую память блока происходит следующим образом:
Скрытый текстextern __shared__ float shared_filter[]; if (threadIdx.y < filterWidth && threadIdx.x < filterWidth) { const int filterOff = threadIdx.y*filterWidth+threadIdx.x; shared_filter[filterOff] = d_filter[filterOff]; } __syncthreads();
Здесь __shared__ в объявлении массива весов фильтра говорит, что эти данные следует разместить в общей памяти блока; extern значит, что размер выделяемой памяти будет задан в месте вызова ядра; __syncthreads — барьер, гарантирующий что все веса фильтра будут перенесены в общую память блока прежде чем какой либо из потоков этого блока продолжит свое выполнение. В дальнейшем, все чтения весов фильтра осуществляются уже из общей памяти блока. - Копируем выходное изображение из памяти устройства в память хоста, освобождаем выделенную память.
Компилируем, запускаем (размер входного изображения — 557x313):
OpenCV time (ms):2
OpenMP time (ms):11
OpenMP similarity:0.00287131
CUDA time kernel (ms): 2.93245
CUDA time full (ms):32
CUDA similarity:0.00287131
CUDA time kernel (ms): 2.93402
CUDA time full (ms):4
CUDA similarity:0.00287131
CUDA time kernel (ms): 2.93267
CUDA time full (ms):4
CUDA similarity:0.00287131
CUDA time kernel (ms): 2.93312
CUDA time full (ms):4
CUDA similarity:0.00287131
Как видим, если не учитывать самый первый запуск CUDA-варианта, получили почти 3-х кратный выигрыш по времени в сравнении с OpenMP вариантом, хотя и не догнали OpenCV вариант — который, кстати, использует OpenCL.
Конфигурация машины, на которой проводились тесты:
Скрытый текст
Процессор: Intel® Core(TM) i7-3615QM CPU @ 2.30GHz.
GPU: NVIDIA GeForce GT 650M, 1024 MB, 900 MHz.
RAM: DD3, 2x4GB, 1600 MHz.
OS: OS X 10.9.5.
Компилятор: g++ (GCC) 4.9.2 20141029.
CUDA компилятор: Cuda compilation tools, release 6.0, V6.0.1.
Поддерживаемая версия OpenMP: OpenMP 4.0.
GPU: NVIDIA GeForce GT 650M, 1024 MB, 900 MHz.
RAM: DD3, 2x4GB, 1600 MHz.
OS: OS X 10.9.5.
Компилятор: g++ (GCC) 4.9.2 20141029.
CUDA компилятор: Cuda compilation tools, release 6.0, V6.0.1.
Поддерживаемая версия OpenMP: OpenMP 4.0.
На сегодня все, в следующей части рассмотрим некоторые фундаментальные алгоритмы GPU.
Весь исходный код доступен на bitbucket.
