Перевод статьи подготовлен в преддверии старта базового курса по машинному обучению.
Проклятие размерности – это серьезная проблема при работе с реальными наборами данных, которые, как правило, являются многомерными. По мере увеличения размерности пространства признаков число конфигураций может расти экспоненциально, и, по итогу число конфигураций, охватываемых наблюдением, уменьшается.
В таком случае метод главных компонент (PCA) будет играть важную роль, эффективно понижая размерность данных и сохраняя при этом как можно больше вариаций, присутствующих в наборе данных.
Давайте вкратце рассмотрим суть метода главных компонент, прежде чем углубляться в проблему.
Основная идея метода главных компонент заключается в том, чтобы уменьшить размерность набора данных, состоящего из большого количества взаимосвязанных переменных, сохраняя при этом максимальное разнообразие, присутствующее в наборе данных.
Определим симметричную матрицу А,
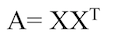
Где Х – матрица m x n независимых переменных, где m – число столбцов, а n – число точек данных. Матрицу А можно разложить следующим образом:
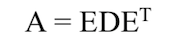
Где D – диагональная матрица, а E — матрица собственных векторов А, расположенных столбцами.
Главные компоненты Х – это собственные вектора XXT, что говорит о том, что направление собственных векторов/главных компонент зависит от вариации независимой переменной (Х).
Почему бездумное применение метода главных компонент является проклятием для задач обучения с учителем?
В литературе часто упоминается использование метода главных компонент в регрессии, а также в задачах мультиколлинеарности. Однако наряду с использованием регрессии на главных компонентах, было много неверных представлений про объяснимость переменной отклика главными компонентами и порядок их важности.
Распространенное заблуждение, которое встречалось несколько раз в различных статьях и книгах, гласит, что в среде обучения с учителем при регрессии на главных компонентах, главные компоненты независимой переменной с маленькими собственными значениями, не будут играть важной роли в объяснении переменной отклика, что приводит нас к цели написания этой статьи. Идея состоит в том, что компоненты с маленькими собственными значениями могут быть столь же важны или даже гораздо более важны, чем основные компоненты с большими собственными значениями при объяснении переменной отклика.
Ниже я перечислю несколько примеров публикаций, о которых я говорил:
[1]. Мэнсфилд и др. (1977, стр. 38) предполагает, что если удаляются только компоненты с небольшой дисперсией, то регрессия не сильно теряет в прогностической способности.
[2]. В книге Ганста и Мейсона (1980) 12 страниц посвящены регрессии на главных компонентах, и большая часть дискуссии предполагает, что удаление главных компонент основано исключительно на их дисперсиях. (стр. 327–328).
[3]. Мостеллер и Тьюрки (1977, стр. 397–398) также аргументируют, что компоненты с небольшой дисперсией вряд ли будут важны в регрессии, очевидно, тем, что природа «хитра», но не «единообразна».
[4]. Хокинг (1976, стр. 31) еще жестче определяет правило сохранения главных компонент в регрессии, основываясь на дисперсии.
Для начала давайте получим корректное математическое обоснование вышеупомянутой гипотезы, а затем дадим небольшие пояснения для лучшего понимания с помощью геометрической визуализации и моделирования.
Допустим,
Y – переменная отклика,
X – Матрица пространства признаков
Z – Стандартизованная версия Х
Пускай
будут собственными значениями ZTZ (корреляционной матрицы), а V – соответствующими собственными векторами, тогда в W=ZV, столбцы в W будут представлять главные компоненты Z. Стандартный метод, применяемый при регрессии на главных компонентах, заключается в регрессии первых m главных компонент на Y, и задачу можно представить через теорему ниже и ее пояснение [2].
Пусть W= (W₁,…,Wp) – собственные вектора Х. Теперь рассмотрим регрессионную модель:
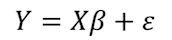
Если истинный вектор коэффициентов регрессии β сонаправлен с j-м собственным вектором ZTZ, то при регрессии Y на W, j-й главный компонент Wⱼ будет вносить вклад в обучение, тогда как оставшиеся не будут вносить вклада в принципе.
Доказательство: Пусть V=(V₁,…,Vp) – матрица собственных векторов ZTZ. Тогда
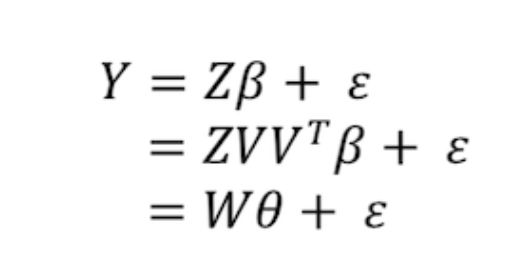
Так как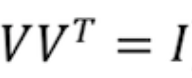
, где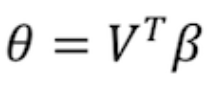 
коэффициенты регрессии выражения.
Если β сонаправлен с j-м собственным вектором Vⱼ, тогда Vⱼ = aβ, где a – ненулевое скалярное значение. Следовательно, θj = Vⱼᵀβ = aβᵀβ и θᴋ = Vᴋᵀβ = 0, где k≠j. Таким образом коэффициент регрессии θᴋ соответствующий Wᴋ равен нулю, при k≠j, соответственно,
Поскольку переменная Wᴋ не уменьшает сумму квадратов, если ее коэффициент регрессии равен 0, то Wj принесет основной вклад, в то время как остальные главные компоненты не внесут никакого вклада.
А теперь давайте смоделируем и получим геометрическое представление вышеперечисленных математических выкладок. Объяснение проиллюстрировано с помощью моделирования двумерного пространства признаков (Х) и одной переменной отклика, чтобы гипотезу можно было легко понять визуально.
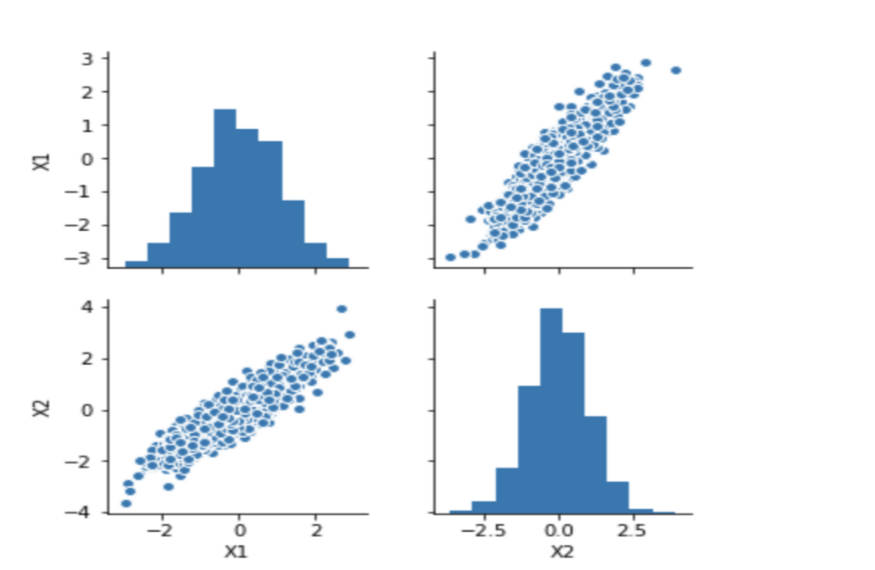
Рисунок 1: Одномерные и двумерные графики для рассматриваемых переменных Х1 и Х2
На первом этапе моделирования пространство признаков было смоделировано с помощью многомерного нормального распределения с очень высокой корреляцией между переменными и главными компонентами.
Рисунок 2: Тепловая карта корреляции для PC1 и PC2 (главных компонент)
Из графика очень хорошо видно, что между главными компонентами нет никакой корреляции. На втором шаге происходит моделирование значений переменной отклика Y таким образом, чтобы направление коэффициента Y главных компонент совпадало с направлением второй главной компоненты.
После получения переменной отклика, корреляционная матрица будет выглядеть примерно следующим образом.
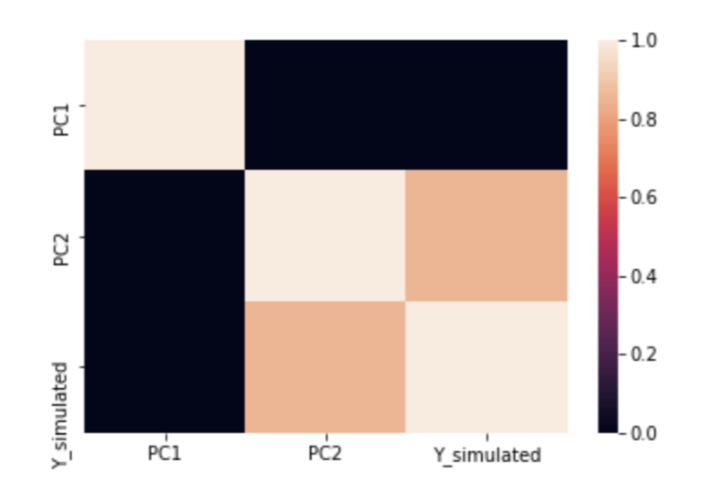
Рисунок 3: Тепловая карта для переменной Y и PC1 и PC2.
На графике хорошо видно, что между Y и PC2 корреляция выше, чем между Y и PC1, что подтверждает нашу гипотезу.
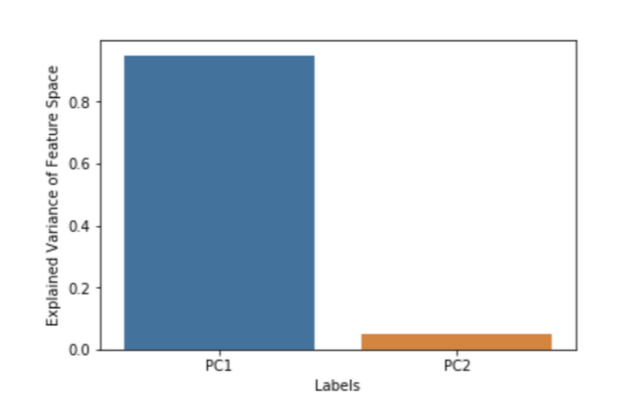
Рисунок 4: Дисперсия пространства признаков, объясняемая PC1 и PC2.
Поскольку на рисунке показано, что PC1 объясняет 95% дисперсии Х, то по логике, изложенной выше, мы должны полностью игнорировать PC2 при регрессии.
Так давайте же последуем ей и увидим, что получится!
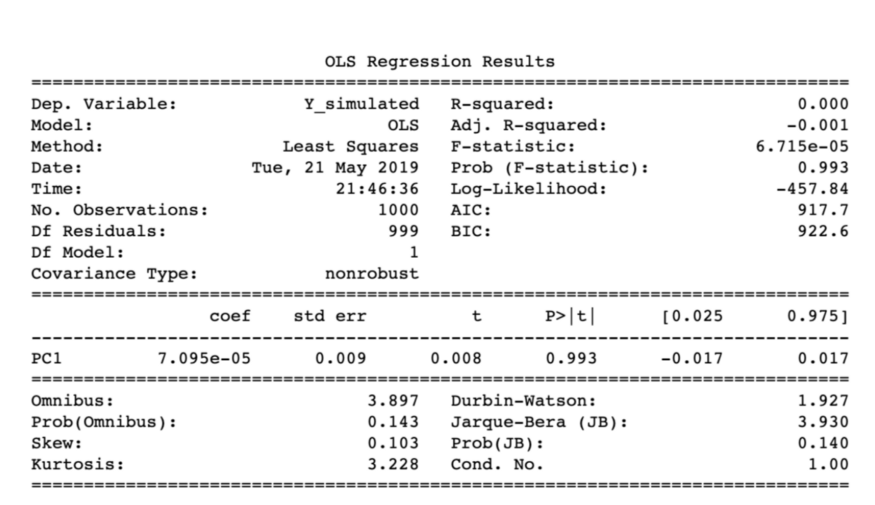
Рисунок 5. Результат регрессии с Y и PC1.
Таким образом R², равный 0, говорит о том, что несмотря на то, что PC1 дает 95% дисперсии Х, она все еще не объясняет переменную отклика.
Теперь сделаем то же самое с PC2, которая объясняет лишь 5% дисперсии Х, и посмотрим, что из этого выйдет.
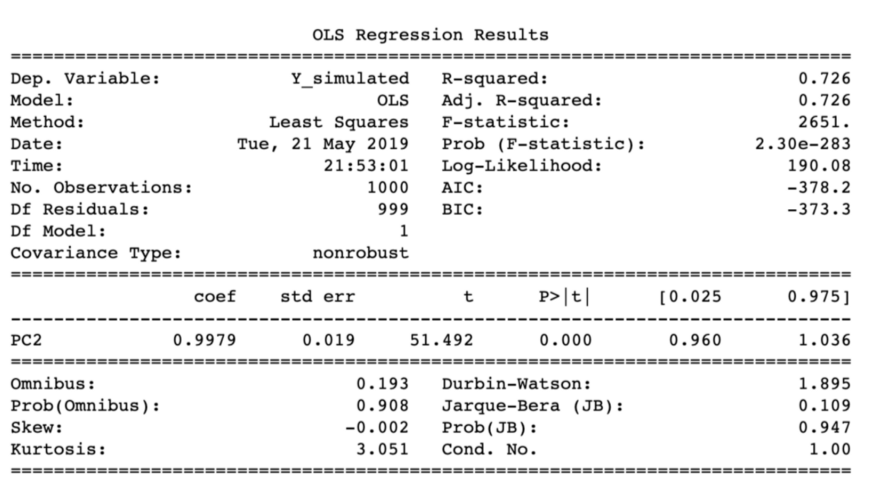
Рисунок 6: Результат регрессии с Y и PC2.
Юху! Вы только посмотрите, что произошло: главная компонента, которая объясняла 5% дисперсии Х, дала 72% дисперсии Y. Есть также и реальные примеры в подтверждение таким ситуациям:
[1] Смит и Кэмпбелл (1980) привели пример из химических технологий, где были 9 регрессорных переменных, и когда дисперсия восьмой главной компоненты составляла 0,06% от общей дисперсии, которая была бы не принята в расчет из-за вышеизложенной логики.
[2] Второй пример предоставили нам Кунг и Шариф (1980). В исследовании, посвящённом прогнозированию даты начала муссонов по десяти метеорологическим переменным, значимыми компонентами были только восьмая, вторая и десятая. В этом примере показано, что даже главная компонента с наименьшим собственным значением будет третьей по значимости с точки зрения объяснения изменчивости переменной отклика.
Приведенные выше примеры показывают, что нецелесообразно удалять главные компоненты с маленькими собственными значениями, так как они влияют лишь на объяснимость в пространстве признаков, но не переменной отклика. Следовательно, нужно сохранять все компоненты в методах понижении размерности при обучении с учителем, таких как регрессия частично наименьших квадратов и регрессия наименьших углов, о которых мы поговорим в дальнейших статьях.
Узнать подробнее о курсе «Machine Learning. Базовый курс», а также посетить бесплатный урок, можно записавшись на бесплатный вебинар по этой ссылке.
Энтропия: как Деревья Решений принимают решения
Пространство высокой размерности и его проклятие
Проклятие размерности – это серьезная проблема при работе с реальными наборами данных, которые, как правило, являются многомерными. По мере увеличения размерности пространства признаков число конфигураций может расти экспоненциально, и, по итогу число конфигураций, охватываемых наблюдением, уменьшается.
В таком случае метод главных компонент (PCA) будет играть важную роль, эффективно понижая размерность данных и сохраняя при этом как можно больше вариаций, присутствующих в наборе данных.
Давайте вкратце рассмотрим суть метода главных компонент, прежде чем углубляться в проблему.
Метод Главных Компонент – определение
Основная идея метода главных компонент заключается в том, чтобы уменьшить размерность набора данных, состоящего из большого количества взаимосвязанных переменных, сохраняя при этом максимальное разнообразие, присутствующее в наборе данных.
Определим симметричную матрицу А,
Где Х – матрица m x n независимых переменных, где m – число столбцов, а n – число точек данных. Матрицу А можно разложить следующим образом:
Где D – диагональная матрица, а E — матрица собственных векторов А, расположенных столбцами.
Главные компоненты Х – это собственные вектора XXT, что говорит о том, что направление собственных векторов/главных компонент зависит от вариации независимой переменной (Х).
Почему бездумное применение метода главных компонент является проклятием для задач обучения с учителем?
В литературе часто упоминается использование метода главных компонент в регрессии, а также в задачах мультиколлинеарности. Однако наряду с использованием регрессии на главных компонентах, было много неверных представлений про объяснимость переменной отклика главными компонентами и порядок их важности.
Распространенное заблуждение, которое встречалось несколько раз в различных статьях и книгах, гласит, что в среде обучения с учителем при регрессии на главных компонентах, главные компоненты независимой переменной с маленькими собственными значениями, не будут играть важной роли в объяснении переменной отклика, что приводит нас к цели написания этой статьи. Идея состоит в том, что компоненты с маленькими собственными значениями могут быть столь же важны или даже гораздо более важны, чем основные компоненты с большими собственными значениями при объяснении переменной отклика.
Ниже я перечислю несколько примеров публикаций, о которых я говорил:
[1]. Мэнсфилд и др. (1977, стр. 38) предполагает, что если удаляются только компоненты с небольшой дисперсией, то регрессия не сильно теряет в прогностической способности.
[2]. В книге Ганста и Мейсона (1980) 12 страниц посвящены регрессии на главных компонентах, и большая часть дискуссии предполагает, что удаление главных компонент основано исключительно на их дисперсиях. (стр. 327–328).
[3]. Мостеллер и Тьюрки (1977, стр. 397–398) также аргументируют, что компоненты с небольшой дисперсией вряд ли будут важны в регрессии, очевидно, тем, что природа «хитра», но не «единообразна».
[4]. Хокинг (1976, стр. 31) еще жестче определяет правило сохранения главных компонент в регрессии, основываясь на дисперсии.
Теоретическое объяснение и понимание
Для начала давайте получим корректное математическое обоснование вышеупомянутой гипотезы, а затем дадим небольшие пояснения для лучшего понимания с помощью геометрической визуализации и моделирования.
Допустим,
Y – переменная отклика,
X – Матрица пространства признаков
Z – Стандартизованная версия Х
Пускай
будут собственными значениями ZTZ (корреляционной матрицы), а V – соответствующими собственными векторами, тогда в W=ZV, столбцы в W будут представлять главные компоненты Z. Стандартный метод, применяемый при регрессии на главных компонентах, заключается в регрессии первых m главных компонент на Y, и задачу можно представить через теорему ниже и ее пояснение [2].Теорема:
Пусть W= (W₁,…,Wp) – собственные вектора Х. Теперь рассмотрим регрессионную модель:
Если истинный вектор коэффициентов регрессии β сонаправлен с j-м собственным вектором ZTZ, то при регрессии Y на W, j-й главный компонент Wⱼ будет вносить вклад в обучение, тогда как оставшиеся не будут вносить вклада в принципе.
Доказательство: Пусть V=(V₁,…,Vp) – матрица собственных векторов ZTZ. Тогда
Так как
, где 
коэффициенты регрессии выражения. Если β сонаправлен с j-м собственным вектором Vⱼ, тогда Vⱼ = aβ, где a – ненулевое скалярное значение. Следовательно, θj = Vⱼᵀβ = aβᵀβ и θᴋ = Vᴋᵀβ = 0, где k≠j. Таким образом коэффициент регрессии θᴋ соответствующий Wᴋ равен нулю, при k≠j, соответственно,
Поскольку переменная Wᴋ не уменьшает сумму квадратов, если ее коэффициент регрессии равен 0, то Wj принесет основной вклад, в то время как остальные главные компоненты не внесут никакого вклада.
Геометрическое значение и моделирование
А теперь давайте смоделируем и получим геометрическое представление вышеперечисленных математических выкладок. Объяснение проиллюстрировано с помощью моделирования двумерного пространства признаков (Х) и одной переменной отклика, чтобы гипотезу можно было легко понять визуально.
Рисунок 1: Одномерные и двумерные графики для рассматриваемых переменных Х1 и Х2
На первом этапе моделирования пространство признаков было смоделировано с помощью многомерного нормального распределения с очень высокой корреляцией между переменными и главными компонентами.
Рисунок 2: Тепловая карта корреляции для PC1 и PC2 (главных компонент)
Из графика очень хорошо видно, что между главными компонентами нет никакой корреляции. На втором шаге происходит моделирование значений переменной отклика Y таким образом, чтобы направление коэффициента Y главных компонент совпадало с направлением второй главной компоненты.
После получения переменной отклика, корреляционная матрица будет выглядеть примерно следующим образом.
Рисунок 3: Тепловая карта для переменной Y и PC1 и PC2.
На графике хорошо видно, что между Y и PC2 корреляция выше, чем между Y и PC1, что подтверждает нашу гипотезу.
Рисунок 4: Дисперсия пространства признаков, объясняемая PC1 и PC2.
Поскольку на рисунке показано, что PC1 объясняет 95% дисперсии Х, то по логике, изложенной выше, мы должны полностью игнорировать PC2 при регрессии.
Так давайте же последуем ей и увидим, что получится!
Рисунок 5. Результат регрессии с Y и PC1.
Таким образом R², равный 0, говорит о том, что несмотря на то, что PC1 дает 95% дисперсии Х, она все еще не объясняет переменную отклика.
Теперь сделаем то же самое с PC2, которая объясняет лишь 5% дисперсии Х, и посмотрим, что из этого выйдет.
Рисунок 6: Результат регрессии с Y и PC2.
Юху! Вы только посмотрите, что произошло: главная компонента, которая объясняла 5% дисперсии Х, дала 72% дисперсии Y. Есть также и реальные примеры в подтверждение таким ситуациям:
[1] Смит и Кэмпбелл (1980) привели пример из химических технологий, где были 9 регрессорных переменных, и когда дисперсия восьмой главной компоненты составляла 0,06% от общей дисперсии, которая была бы не принята в расчет из-за вышеизложенной логики.
[2] Второй пример предоставили нам Кунг и Шариф (1980). В исследовании, посвящённом прогнозированию даты начала муссонов по десяти метеорологическим переменным, значимыми компонентами были только восьмая, вторая и десятая. В этом примере показано, что даже главная компонента с наименьшим собственным значением будет третьей по значимости с точки зрения объяснения изменчивости переменной отклика.
Вывод
Приведенные выше примеры показывают, что нецелесообразно удалять главные компоненты с маленькими собственными значениями, так как они влияют лишь на объяснимость в пространстве признаков, но не переменной отклика. Следовательно, нужно сохранять все компоненты в методах понижении размерности при обучении с учителем, таких как регрессия частично наименьших квадратов и регрессия наименьших углов, о которых мы поговорим в дальнейших статьях.
Источники
[1] Jolliffe, Ian T. “A Note on the Use of Principal Components in Regression.” Journal of the Royal Statistical Society. Series C (Applied Statistics), vol. 31, no. 3, 1982, pp. 300–303. JSTOR, www.jstor.org/stable/2348005.
[2] Hadi, Ali S., and Robert F. Ling. “Some Cautionary Notes on the Use of Principal Components Regression.” The American Statistician, vol. 52, no. 1, 1998, pp. 15–19. JSTOR, www.jstor.org/stable/2685559.
[3] HAWKINS, D. M. (1973). On the investigation of alternative regressions by principal component analysis. Appl. Statist., 22, 275–286
[4] MANSFIELD, E. R., WEBSTER, J. T. and GUNST, R. F. (1977). An analytic variable selection technique for principal component regression. Appl. Statist., 26, 34–40.
[5] MOSTELLER, F. and TUKEY, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Reading, Mass.: Addison-Wesley
[6] GUNST, R. F. and MASON, R. L. (1980). Regression Analysis and its Application: A Data-oriented Approach. New York: Marcel Dekker.
[7] JEFFERS, J. N. R. (1967). Two case studies in the application of principal component analysis. Appl. Statist., 16, 225- 236. (1981). Investigation of alternative regressions: some practical examples. The Statistician, 30, 79–88.
[8] KENDALL, M. G. (1957). A Course in Multivariate Analysis. London: Griffin.
[2] Hadi, Ali S., and Robert F. Ling. “Some Cautionary Notes on the Use of Principal Components Regression.” The American Statistician, vol. 52, no. 1, 1998, pp. 15–19. JSTOR, www.jstor.org/stable/2685559.
[3] HAWKINS, D. M. (1973). On the investigation of alternative regressions by principal component analysis. Appl. Statist., 22, 275–286
[4] MANSFIELD, E. R., WEBSTER, J. T. and GUNST, R. F. (1977). An analytic variable selection technique for principal component regression. Appl. Statist., 26, 34–40.
[5] MOSTELLER, F. and TUKEY, J. W. (1977). Data Analysis and Regression: A Second Course in Statistics. Reading, Mass.: Addison-Wesley
[6] GUNST, R. F. and MASON, R. L. (1980). Regression Analysis and its Application: A Data-oriented Approach. New York: Marcel Dekker.
[7] JEFFERS, J. N. R. (1967). Two case studies in the application of principal component analysis. Appl. Statist., 16, 225- 236. (1981). Investigation of alternative regressions: some practical examples. The Statistician, 30, 79–88.
[8] KENDALL, M. G. (1957). A Course in Multivariate Analysis. London: Griffin.
Узнать подробнее о курсе «Machine Learning. Базовый курс», а также посетить бесплатный урок, можно записавшись на бесплатный вебинар по этой ссылке.
Читать ещё:
Энтропия: как Деревья Решений принимают решения
