
Команда Big Data МТС активно извлекает знания из имеющихся данных и решает большое количество задач для бизнеса. Один из типов задач машинного обучения, с которыми мы сталкиваемся – это задачи моделирования uplift. С помощью этого подхода оценивается эффект от коммуникации с клиентами и выбирается группа, которая наиболее подвержена влиянию.
Такой класс задач прост в реализации, но не получил большого распространения в литературе про машинное обучение. Небольшой цикл статей, подготовленный Ириной Елисовой (iraelisova) и Максимом Шевченко (maks-sh), можно рассматривать как руководство к решению таких задач. В рамках него мы познакомимся с uplift моделями, рассмотрим, чем они отличаются от других подходов, и разберем их реализации.
Все туториалы серии
Содержание статьи
Введение
Обычно продвижение продуктов происходит за счет коммуникации с клиентом через различные каналы: смс, push, сообщения чат-бота в социальных сетях и многие другие. Формирование сегментов для продвижения сейчас решается с помощью машинного обучения несколькими способами:

- Look-alike модель оценивает вероятность того, что клиент выполнит целевое действие. В качестве обучающей выборки используются известные позитивные объекты (например, пользователи, установившие приложение) и случайные негативные объекты (сэмплирование небольшой подвыборки из всех остальных клиентов, у кого это приложение не было установлено). Модель будет пытаться искать клиентов, похожих на тех, кто совершил целевое действие.
- Response модель оценивает вероятность того, что клиент выполнит целевое действие при условии коммуникации. В этом случае обучающей выборкой являются данные, собранные после некоторого взаимодействия с клиентами. В отличии от первого подхода в нашем распоряжении имеются реальные позитивные и негативные наблюдения (например, клиент оформил кредитную карту или отказался).
- Uplift модель оценивает чистый эффект от коммуникации, пытаясь выбрать только тех клиентов, которые совершат целевое действие только при нашем взаимодействии. Модель оценивает разницу в поведении клиента при наличии воздействия и при его отсутствии.
Когда же следует прогнозировать uplift? Обычно его используют, когда целевое действие выполняется клиентами с достаточно большой вероятностью без каких-либо коммуникаций. Например, мы хотим прорекламировать достаточно популярный продукт, но при этом не хотим тратить бюджет на клиентов, которые и без нас купят этот продукт. Если же продукт не очень популярный и его в основном покупают только при продвижении, то задача сводится к response моделированию.
Нельзя просто взять и обучить модель
Для оптимизации эффекта от воздействия хочется посчитать разницу реакций человека при наличии коммуникации и при ее отсутствии. Проблема в том, что мы не можем одновременно совершить коммуникацию (например, послать смс) и не совершить коммуникацию (не послать смс). Обозначим дельту потенциальных реакций
где

Зная признаковое описание
Ни causal effect
Где
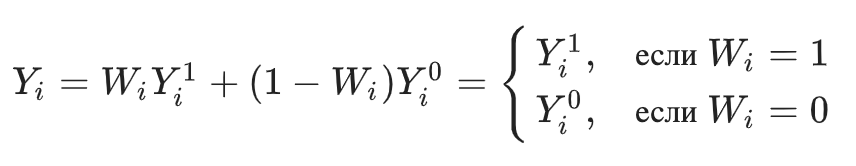
Где
Стоит отметить, что формула для uplift применима только при следующем предположении об условной независимости (Conditional Independence Assumption — CIA): разделение на целевую и контрольную группу происходит случайно, а не в зависимости от значения какого-то признака. Потенциальная реакция объекта
При этом наблюдаемая реакция объекта
Дизайн эксперимента
Итак, нам нужно оценить разницу между двумя событиями, которые являются взаимоисключающими для конкретного клиента (либо мы коммуницируем с человеком, либо нет; нельзя одновременно совершить два этих действия). Именно поэтому для построения моделей uplift предъявляются дополнительные требования к исходным данным.
Для получения обучающей выборки для моделирования uplift необходимо провести эксперимент:
- Случайным образом разбить репрезентативную часть клиентской базы на целевую и контрольную группы;
- Запустить пилот маркетинговой кампании на целевую группу.
Единственным отличием эксперимента от будущей кампании должен быть тот факт, что в первом случае для взаимодействия мы выбираем случайных клиентов, а во втором – клиентов на основе спрогнозированного значения uplift. Если маркетинговая кампания существенно отличается от эксперимента, используемого для сбора данных о выполнении целевых действий клиентами, то построенная модель может быть менее надежной и точной.
Собранные данные об откликах на маркетинговое предложение, полученные в рамках такого эксперимента, позволят нам в дальнейшем построить модель прогнозирования uplift.
Перед проведением основной кампании рекомендуется аналогично эксперименту случайным образом выбрать небольшую часть клиентской базы и разбить ее на контрольную и целевую группы. С помощью этих данных можно будет не только адекватно оценить эффективность кампании, но и собрать дополнительные данные для дальнейшего переобучения модели.
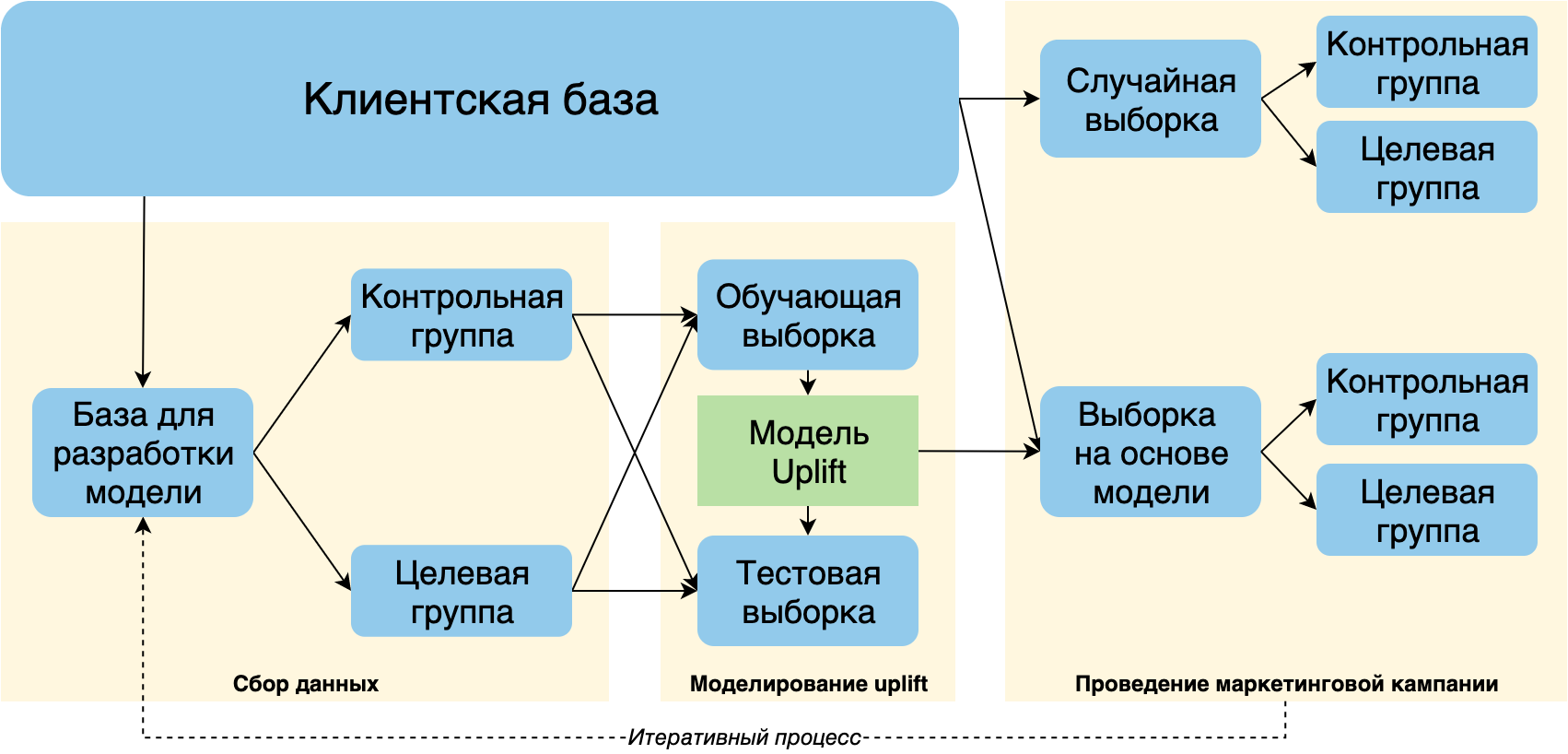
Схема взята и адаптирована из [1]
Кроме того, рекомендуется настраивать разработку uplift модели и запуск кампании как итеративный процесс: на каждой итерации будут собираться новые обучающие данные об откликах, которые состоят из комбинирования случайной подвыборки клиентов и клиентов, выбранных моделью.
Результаты воздействия на клиентов, выбранных моделью, не хотелось бы использовать в качестве обучающей выборки, так как клиенты были взяты не случайным образом. Однако эти данные представляют большую ценность, поэтому их следует изучить и использовать для дальнейшего совершенствования модели и увеличения отклика от будущих кампаний.
Типы клиентов
Принято выделять 4 типа клиентов по реакции на коммуникацию:

- Не беспокоить (Do-Not-Disturbs) — человек, который будет реагировать негативно, если с ним прокоммуницировать.
- Потерянный (Lost Causes) — человек, который никогда не совершит целевое действие, вне зависимости от коммуникаций. Взаимодействие с такими клиентами не приносит дополнительного дохода, но создает дополнительные затраты.
- Лояльный (Sure Things) — человек, который будет реагировать положительно, несмотря ни на что. Это самый лояльный вид клиентов. По аналогии с предыдущим пунктом, такие клиенты также расходуют бюджет.
- Убеждаемый (Persuadables) — это человек, который положительно реагирует на предложение, но при его отсутствии не выполнил бы целевого действия. Это те люди, которых мы хотели бы определить нашей моделью, чтобы с ними прокоммуницировать.
Стоит отметить, что в зависимости от клиентской базы и особенностей компании возможно отсутствие некоторых из этих типов клиентов. Кроме того, выполнение целевого действия сильно зависит от различных характеристик самой кампании, например, канала взаимодействия или типа и размера предлагаемого маркетингового предложения. Для максимизации прибыли следует также подбирать эти параметры.
Таким образом, предсказывая uplift и выбирая топ предсказаний, мы хотим найти только один из четырех типов — убеждаемый. Есть несколько способов это сделать.
Одна модель с признаком коммуникации
Treatment Dummy approach, Solo model approach, Single model approach, S-Learner
Самое простое и интуитивное решение: модель обучается одновременно на двух группах, при этом бинарный флаг коммуникации выступает в качестве дополнительного признака. Каждый объект из тестовой выборки скорим дважды: с флагом коммуникации равным 1 и равным 0. Вычитая вероятности по каждому наблюдению, получим искомый uplift.

В некоторых статьях, например [2], предлагается увеличить количество признаков вдвое, добавив произведение каждого признака на флаг взаимодействия:

Две независимые модели
Two models approach, T-learner, difference two models
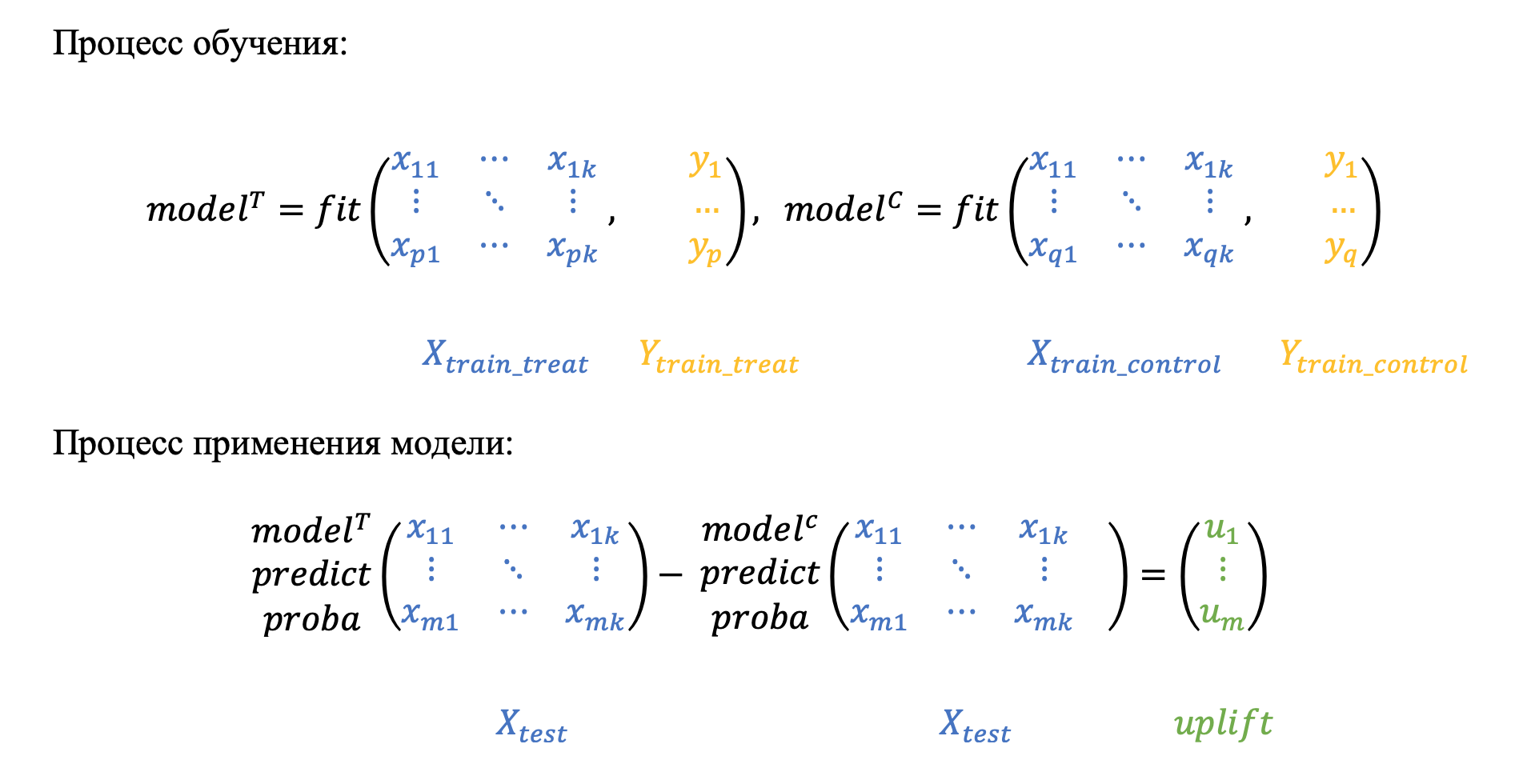
Подход с двумя моделями один из самых популярных и достаточно часто встречается в статьях, например [3] и [4]. Метод заключается в отдельном моделировании двух условных вероятностей на целевой и контрольной группах, а именно:
- Строится первая модель, оценивающая вероятность выполнения целевого действия среди клиентов, с которыми мы взаимодействовали.
- Строится вторая модель, оценивающая ту же вероятность, но среди клиентов, с которыми мы не производили коммуникацию.
- Затем для каждого клиента рассчитывается разность оценок вероятностей двух моделей.
Две зависимые модели (зависимое представление данных)
Dependent Data Representation, Dependent Feature Representation
Подход зависимого представления данных, представленный в [5], основан на методе цепочек классификаторов, первоначально разработанном для задач многоклассовой классификации. Идея состоит в том, что при наличии
затем выполним предсказания
Чтобы получить uplift для каждого наблюдения, вычислим разницу:
Так второй классификатор изучает разницу между ожидаемым результатом в тесте и контроле, т.е. сам uplift.

Аналогичным образом можно сначала обучить классификатор
Две зависимые модели (перекрестная зависимость)
X-learner
Метод основывается на построении двух моделей, так же, как и в двух предыдущих подходах. Авторы статьи [6] рекомендуют применять его тогда, когда целевая группа достаточно маленькая. В этом случае есть риск, что модель, построенная на целевой группе, будет обладать недостаточной обобщающей способностью. Поэтому создается перекрестная зависимость двух моделей, чтобы усилить одну модель данными другой.
1. Сначала обучаем параллельно две модели: одну на контрольной группе, другую — на целевой (как в методе с двумя независимыми моделями):

2. Затем преобразуем обе целевые переменные, используя предсказания контрольной модели на данных целевой группы и предсказания целевой модели на данных контрольной группы. Полученные величины обозначаются как

Если оценки
3. Обучим две новые модели на преобразованных таргетах
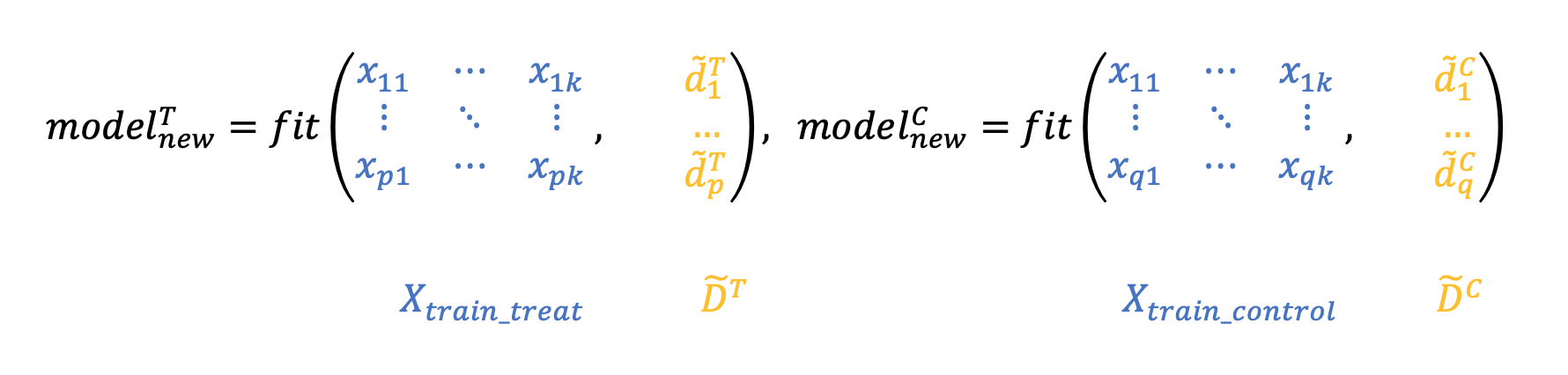
4. Взвешенная с некоторым коэффициентом

Рекомендуется выбирать
Заключение
В этой статье были рассмотрены особенности uplift моделей, процесс сбора данных и проведения маркетинговых кампаний, а также базовые методы моделирования uplift. В следующей части мы продолжим говорить о более интересных подходах.
Статья написана в соавторстве с Ириной Елисовой (iraelisova)
Полезные ссылки
- Jupyter notebook с примером использования питоновской библиотеки scikit-uplift от Максима Шевченко (maks-sh)
- Доклад про uplift моделирование от Ирины Елисовой (iraelisova) на Data Fest 6
- Доклад про аплифт моделирование от Валерия Бабушкина (venheads)
- Доклад про рассылку персональных сообщений физ лицам клиентам банка от Александра Фонарева на Data Fest 5
- Profit Driven Business Analytics by Verbeke, Wouter & Baesens, Bart & Bravo, Cristián – отличная книга, глава в которой посвящена uplift моделированию
Источники
- [1] Verbeke, Wouter & Baesens, Bart & Bravo, Cristián. (2018). Profit Driven Business Analytics: A Practitioner's Guide to Transforming Big Data into Added Value.
- [2] Lo, Victor. (2002). The True Lift Model — A Novel Data Mining Approach to Response Modeling in Database Marketing… SIGKDD Explorations. 4. 78-86.
- [3] Radcliffe, N.J. (2007). Using control groups to target on predicted lift: Building and assessing uplift model. Direct Market J Direct Market Assoc Anal Council, 1:14–21, 2007.
- [4] Nassif, Houssam & Kuusisto, F. & Burnside, Elizabeth & Shavlik, J… (2014). Uplift modeling with ROC: An SRL case study. CEUR Workshop Proceedings. 1187. 40-45.
- [5] Betlei, Artem & Diemert, Eustache & Amini, Massih-Reza. (2018). Uplift Prediction with Dependent Feature Representation in Imbalanced Treatment and Control Conditions: 25th International Conference, ICONIP 2018, Siem Reap, Cambodia, December 13–16, 2018, Proceedings, Part V. 10.1007/978-3-030-04221-9_5.
- [6] Zhao, Yan & Fang, Xiao & Simchi-Levi, David. (2017). Uplift Modeling with Multiple Treatments and General Response Types. 10.1137/1.9781611974973.66.
- [7] Gutierrez, P., & Gérardy, J. Y. (2017). Causal Inference and Uplift Modelling: A Review of the Literature. In International Conference on Predictive Applications and APIs (pp. 1-13).
