skillfactory_school 27 окт 2020 в 18:48

Реализуем и сравниваем оптимизаторы моделей в глубоком обучении

14 мин

42K

Блог компании SkillfactoryPython*Big Data*Машинное обучение*Data Engineering*

Туториал

Перевод

Автор оригинала: Amar Rocade

Реализуем и сравниваем 4 популярных оптимизатора обучения нейронных сетей: оптимизатор импульса, среднеквадратичное распространение, мини-пакетный градиентный спуск и адаптивную оценку момента. Репозиторий, много кода на Python и его вывод, визуализации и формулы — всё это под катом.

Введение

Модель — это результат работы алгоритма машинного обучения, выполняемого на некоторых данных. Модель представляет собой то, что было изучено алгоритмом. Это «вещь», которая сохраняется после запуска алгоритма на обучающих данных и представляет собой правила, числа и любые другие структуры данных, специфичные для алгоритма и необходимые для предсказания.

Что такое оптимизатор?

Прежде чем перейти к этому, мы должны знать, что такое функция потерь. Функция потерь — это мера того, насколько хорошо ваша модель прогнозирования предсказывает ожидаемый результат (или значение). Функция потерь также называется функцией затрат (дополнительная информация здесь).

В процессе обучения мы стараемся минимизировать потери функции и обновлять параметры для повышения точности. Параметры нейронной сети — это обычно веса связей. В этом случае параметры изучаются на этапе обучения. Итак, сам алгоритм (и входные данные) настраивает эти параметры. Более подробную информацию можно найти здесь.

Таким образом, оптимизатор — это метод достижения лучших результатов, помощь в ускорении обучения. Другими словами, это алгоритм, используемый для незначительного изменения параметров, таких как веса и скорость обучения, чтобы модель работала правильно и быстро. Здесь рассмотрим базовый обзор различных используемых в глубоком обучении оптимизаторов и сделаем простую модель, чтобы понять реализацию этой модели. Я настоятельно рекомендую клонировать этот репозиторий и вносить изменения, наблюдая за моделями поведения.

Некоторые часто используемые термины:

Обратное распространение

Цели обратного распространения просты: отрегулировать каждый вес в сети согласно тому, насколько он способствует ошибке в целом. Если итеративно уменьшать погрешность каждого веса, то в конечном счете получится ряд весов, которые дают хорошие прогнозы. Мы находим наклон каждого параметра для функции потерь и обновляем параметры, вычитая наклон (дополнительная информация здесь).

Градиентный спуск

Градиентный спуск — это алгоритм оптимизации, используемый для минимизации некоторой функции путем итеративного движения в направлении самого крутого спуска, определяемого отрицательным значением градиента. В глубоком обучении мы используем градиентный спуск для обновления параметров модели (дополнительная информация здесь).

Гиперпараметры

Гиперпараметр модели — это внешняя по отношению к модели конфигурация, значение которой не может оцениваться по данным. Например количество скрытых нейронов, скорость обучения и т. д. Мы не можем оценить скорость обучения по данным (дополнительная информация здесь).

Скорость обучения

Скорость обучения (α) — это параметр настройки в алгоритме оптимизации, определяющий размер шага на каждой итерации при движении к минимуму функции потерь (дополнительная информация здесь).

1. Стохастический градиентный спуск (особенно мини-пакетный)

Мы используем один пример за раз при обучении модели (в чистом SGD) и обновления параметра. Но мы должны использовать еще один для цикла. Это займет много времени. Поэтому используем мини-пакетный SGD.

Мини-пакетный градиентный спуск стремится сбалансировать устойчивость стохастического градиентного спуска и эффективность пакетного градиентного спуска. Это наиболее распространенная реализация градиентного спуска, используемая в области глубокого обучения. В мини-пакетном SGD при обучении модели мы берем группу примеров (например, 32, 64 примера и т. д.). Такой подход работает лучше, потому что требуется единственный цикл для мини-пакетов, а не для каждого примера. Мини-пакеты выбираются случайным образом для каждой итерации, но почему? Когда мини-пакеты выбираются случайным образом, то при застревании в локальных минимумах некоторые шумные шаги могут привести к выходу из этих минимумов. Зачем нам этот оптимизатор?

Частота обновления параметров выше, чем в простом пакетном градиентном спуске, что позволяет обеспечить сходимость надежнее, избегая локальных минимумов.
Пакетные обновления обеспечивают процесс вычислительно эффективнее, чем стохастический градиентный спуск.
Если у вас немного оперативной памяти, то мини-пакеты — это лучший вариант. Пакетирование эффективно благодаря отсутствию всех обучающих данных в памяти и реализациям алгоритмов.

Как генерировать случайные мини-пакеты?

def RandomMiniBatches(X, Y, MiniBatchSize):

    m = X.shape[0]  
    miniBatches = [] 
   
    permutation = list(np.random.permutation(m))
    shuffled_X = X[permutation, :]
    shuffled_Y = Y[permutation, :].reshape((m,1))   #sure for uptpur shape

    num_minibatches = m // MiniBatchSize 
    for k in range(0, num_minibatches):
        miniBatch_X = shuffled_X[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch_Y = shuffled_Y[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    #handeling last batch
    if m % MiniBatchSize != 0:
        # end = m - MiniBatchSize * m // MiniBatchSize
        miniBatch_X = shuffled_X[num_minibatches * MiniBatchSize:, :]
        miniBatch_Y = shuffled_Y[num_minibatches * MiniBatchSize:, :]

        miniBatch = (miniBatch_X, miniBatch_Y)
        miniBatches.append(miniBatch)
    
    return miniBatches

Каким будет формат модели?

Я даю обзор модели на случай, если вы новичок в глубоком обучении. Она выглядит примерно так:

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 64)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)             #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                          #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob)  #BACKWARD PROPAGATION 
            params = update_params(params, grad, beta=0.9,learning_rate=learning_rate)
    return params

На следующем рисунке видно, в SGD присутствуют огромные колебания. Вертикальное движение не обязательно: мы хотим движения только горизонтально. Если уменьшить вертикальное движение и увеличить горизонтальное, модель будет учиться быстрее, согласны?

Как минимизировать нежелательные колебания? Следующие оптимизаторы минимизируют их и помогают ускорить обучение.

2. Оптимизатор импульса

В SGD или градиентном спуске много колебаний. Нужно двигаться вперед, а не вверх-вниз. Мы должны увеличить скорость обучения модели в правильном направлении, и мы сделаем это с помощью оптимизатора импульса.

Как видно на рисунке выше, зеленая цветовая линия оптимизатора импульса быстрее других. Важность быстрого обучения можно увидеть, когда у вас большие наборы данных и много итераций. Как внедрить этот оптимизатор?

Нормально значение β около 0,9

Видно, что мы создали два параметра — vdW, и vdb — из параметров обратного распространения. Рассмотрим значение β = 0.9, тогда уравнения приобретает вид:

vdw= 0.9 * vdw + 0.1 * dw
vdb = 0.9 * vdb + 0.1 * db

Как вы видите, vdw больше зависит от предыдущего значения vdw, а не dw. Когда визуализация — это график, можно увидеть, что оптимизатор импульса учитывает прошлые градиенты, чтобы сгладить обновление. Вот почему возможно минимизировать колебания. Когда мы использовали SGD, пройденный мини-пакетным градиентным спуском путь колебался в сторону конвергенции. Оптимизатор импульса помогает уменьшить эти колебания.

def update_params_with_momentum(params, grads, v, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):

        # HERE WE COMPUTING THE VELOCITIES 
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
        
        #updating parameters W and b
        params["W" + str(l + 1)] = params["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        params["b" + str(l + 1)] = params["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
    return params

Репозиторий находится здесь

3. Среднеквадратичное распространение

Среднеквадратичное распространение корня (RMSprop) — это экспоненциально затухающее среднее значение. Существенным свойством RMSprop является то, что вы не ограничены только суммой прошлых градиентов, но вы более ограничены градиентами последних временных шагов. RMSprop вносит свой вклад в экспоненциально затухающее среднее значение прошлых «квадратичных градиентов». В RMSProp мы пытаемся уменьшить вертикальное движение, используя среднее значение, потому что они суммируются приблизительно до 0, принимая среднее значение. RMSprop предоставляет среднее значение для обновления.

Источник

Посмотрите на приведенный ниже код. Это даст вам базовое представление о том, как внедрить этот оптимизатор. Все то же самое, что и с SGD, мы должны изменить функцию обновления.

def initilization_RMS(params):
    s = {}
    for i in range(len(params)//2 ):
        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return s

def update_params_with_RMS(params, grads,s, beta, learning_rate):
    
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 
        s["dW" + str(l)]= beta * s["dW" + str(l)] + (1 - beta) * np.square(grads['dW' + str(l)])
        s["db" + str(l)] = beta * s["db" + str(l)] + (1 - beta) * np.square(grads['db' + str(l)])
        
        #updating parameters W and b
        params["W" + str(l)] = params["W" + str(l)] - learning_rate * grads['dW' + str(l)] / (np.sqrt( s["dW" + str(l)] )+ pow(10,-4))
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * grads['db' + str(l)] / (np.sqrt( s["db" + str(l)]) + pow(10,-4))

    return params

4. Оптимизатор Adam

Adam — один из самых эффективных алгоритмов оптимизации в обучении нейронных сетей. Он сочетает в себе идеи RMSProp и оптимизатора импульса. Вместо того чтобы адаптировать скорость обучения параметров на основе среднего первого момента (среднего значения), как в RMSProp, Adam также использует среднее значение вторых моментов градиентов. В частности, алгоритм вычисляет экспоненциальное скользящее среднее градиента и квадратичный градиент, а параметры beta1 и beta2 управляют скоростью затухания этих скользящих средних. Каким образом?

def initilization_Adam(params):
    s = {}
    v = {}
    for i in range(len(params)//2 ):

        v["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        v["db" + str(i)] = np.zeros(params["b" + str(i)].shape)

        s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
        s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
    return v, s
    
def update_params_with_Adam(params, grads,v, s, beta1,beta2, learning_rate,t):
    epsilon = pow(10,-8)
    v_corrected = {}                         
    s_corrected = {} 
    # grads has the dw and db parameters from backprop
    # params  has the W and b parameters which we have to update 
    for l in range(len(params) // 2 ):
        # HERE WE COMPUTING THE VELOCITIES 

        v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads['dW' + str(l)]
        v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads['db' + str(l)]

        v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))
        v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))


        s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.power(grads['dW' + str(l)], 2)
        s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.power(grads['db' + str(l)], 2)

        s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))
        s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))

        params["W" + str(l)] = params["W" + str(l)] - learning_rate * v_corrected["dW" + str(l)] / np.sqrt(s_corrected["dW" + str(l)] + epsilon)
        params["b" + str(l)] = params["b" + str(l)] - learning_rate * v_corrected["db" + str(l)] / np.sqrt(s_corrected["db" + str(l)] + epsilon)
    return params

Гиперпараметры

значение β1(beta1) почти 0,9
β2 (бета2) — почти 0.999
ε — предотвращение деления на ноль ( 10^-8) (не слишком сильно влияет на обучение)

Зачем этот оптимизатор?

Его преимущества:

Простая реализация.
Вычислительная эффективность.
Небольшие требования к памяти.
Инвариант к диагональному масштабированию градиентов.
Хорошо подходит для больших с точки зрения данных и параметров задач.
Подходит для нестационарных целей.
Подходит для задач с очень шумными или разреженными градиентами.
Гиперпараметры имеют наглядную интерпретацию и обычно требуют небольшой настройки.

Давайте построим модель и посмотрим, как гиперпараметры ускоряют обучение

Давайте проведем практическую демонстрацию того, как ускорить обучение. В этой статье мы не будем объяснять другие вещи (инициализацию, отсев, forward_prop, back_prop, градиентный спуск и т. д.). Необходимые дл обучения Функции уже встроены в NumPy. Если вы хотите взглянуть на это, вот ссылка!

Давайте начнем!

Я создаю обобщенную модельную функцию, работающую для всех обсуждаемых здесь оптимизаторов.

1. Инициализация:

Мы инициализируем параметры с помощью функции инициализации, которая принимает входные данные, такие как features_size (в нашем случае 12288) и скрытый массив размеров (мы использовали [100,1]) и данный вывод как параметры инициализации. Существует другой метод инициализации. Я призываю прочитать эту статью.

def initilization(input_size,layer_size):
    params = {}
    np.random.seed(0) 
    params['W' + str(0)] = np.random.randn(layer_size[0], input_size) * np.sqrt(2 / input_size)
    params['b' + str(0)] = np.zeros((layer_size[0], 1))
    for l in range(1,len(layer_size)):
        params['W' + str(l)] = np.random.randn(layer_size[l],layer_size[l-1]) * np.sqrt(2/layer_size[l])
        params['b' + str(l)] = np.zeros((layer_size[l],1))
    return params

2. Прямое распространение:

В этой функции входные данные — это X, а также параметры, протяженность скрытых слоев и отсев, которые используются в технике отсева.

Я установил значение 1, так что никакого эффекта на тренировке не будет видно. Если ваша модель переобучена, то вы можете установить другое значение. Я применяю отсев только на четных слоях.

Мы вычисляем значение активации для каждого слоя с помощью функции forward_activation.

#activations-----------------------------------------------
def forward_activation(A_prev, w, b, activation):
    z = np.dot(A_prev, w.T) + b.T
    if activation == 'relu':
        A = np.maximum(0, z)
    elif activation == 'sigmoid':
        A = 1/(1+np.exp(-z))
    else:
        A = np.tanh(z)
    return A


#________model forward ____________________________________________________________________________________________________________
def model_forward(X,params, L,keep_prob):
    cache = {}
    A =X

    for l in range(L-1):
        w = params['W' + str(l)]
        b = params['b' + str(l)]
        A = forward_activation(A, w, b, 'relu')
        if l%2 == 0:
            cache['D' + str(l)] = np.random.randn(A.shape[0],A.shape[1]) < keep_prob
            A = A * cache['D' + str(l)] / keep_prob
        cache['A' + str(l)] = A
    w = params['W' + str(L-1)]
    b = params['b' + str(L-1)]
    A = forward_activation(A, w, b, 'sigmoid')
    cache['A' + str(L-1)] = A
    return cache, A

3. Обратное распространение:

Здесь мы пишем функцию обратного распространения. Она вернет grad (наклон). Мы используем grad при обновлении параметров, (если вы об этом не знаете). Рекомендую прочитать эту статью.

def backward(X, Y, params, cach,L,keep_prob):
    grad ={}
    m = Y.shape[0]

    cach['A' + str(-1)] = X
    grad['dz' + str(L-1)] = cach['A' + str(L-1)] - Y
    cach['D' + str(- 1)] = 0
    for l in reversed(range(L)):
        grad['dW' + str(l)] = (1 / m) * np.dot(grad['dz' + str(l)].T, cach['A' + str(l-1)])
        grad['db' + str(l)] = 1 / m * np.sum(grad['dz' + str(l)].T, axis=1, keepdims=True)
        if l%2 != 0:
            grad['dz' + str(l-1)] = ((np.dot(grad['dz' + str(l)], params['W' + str(l)]) * cach['D' + str(l-1)] / keep_prob) *
                                 np.int64(cach['A' + str(l-1)] > 0))
        else :
            grad['dz' + str(l - 1)] = (np.dot(grad['dz' + str(l)], params['W' + str(l)]) *
                                       np.int64(cach['A' + str(l - 1)] > 0))

    return grad

Мы уже видели функцию обновления оптимизаторов, так что используем ее здесь. Внесем небольшие изменения в функцию модели из обсуждения SGD.

def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
    L = len(hidden_size)
    params = initilization(X.shape[1], hidden_size)
    costs = []
    itr  = []

    if optimizer == 'momentum':
        v = initilization_moment(params)

    elif optimizer == 'rmsprop':
        s = initilization_RMS(params)

    elif optimizer == 'adam' :
        v,s = initilization_Adam(params)

    for i in range(1,num_iter):
        MiniBatches = RandomMiniBatches(X, Y, 32)   # GET RAMDOMLY MINIBATCHES
        p , q = MiniBatches[2]
        for MiniBatch in MiniBatches:               #LOOP FOR MINIBATCHES

            (MiniBatch_X, MiniBatch_Y) = MiniBatch

            cache, A = model_forward(MiniBatch_X, params, L,keep_prob)     #FORWARD PROPOGATIONS
            cost = cost_f(A, MiniBatch_Y)                                  #COST FUNCTION
            grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob) #BACKWARD PROPAGATION 

            if optimizer == 'momentum':
                params = update_params_with_momentum(params, grad, v, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'rmsprop':
               params = update_params_with_RMS(params, grad, s, beta=0.9,learning_rate=learning_rate)

            elif optimizer == 'adam' :
                params = update_params_with_Adam(params, grad,v, s, beta1=0.9,beta2=0.999,  learning_rate=learning_rate,t=i)                                         #UPDATE PARAMETERS
            elif optimizer == "minibatch":
                params = update_params(params, grad,learning_rate=learning_rate) 

           
        
        if i%5 == 0:
            costs.append(cost)
            itr.append(i)
            if i % 100 == 0 :
                print('cost of iteration______{}______{}'.format(i,cost))
    return params,costs,itr

Обучение с мини-пакетами

params, cost_sgd,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='minibatch')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Вывод при подходе с мини-пакетами:

cost of iteration______100______0.35302967575683797 
cost of iteration______200______0.472914548745098 
cost of iteration______300______0.4884728238471557 
cost of iteration______400______0.21551100063345618
 
train_accuracy------------ 0.8494208494208494

Обучение с оптимизатором импульса

params,cost_momentum, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='momentum')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Вывод оптимизатора импульса:

cost of iteration______100______0.36278494129038086 
cost of iteration______200______0.4681552335189021 
cost of iteration______300______0.382226159384529 
cost of iteration______400______0.18219310793752702 train_accuracy------------ 0.8725868725868726

Тренировка с RMSprop

params,cost_rms,itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='rmsprop')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Вывод RMSprop:

cost of iteration______100______0.2983858963793841 
cost of iteration______200______0.004245700579927428 
cost of iteration______300______0.2629426607580565 
cost of iteration______400______0.31944824707807556 train_accuracy------------ 0.9613899613899614

Тренировка с Adam

params,cost_adam, itr = model(X_train, Y_train, learning_rate = 0.01,
               num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='adam')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))

Вывод Adam:

cost of iteration______100______0.3266223660473619 
cost of iteration______200______0.08214547683157716 
cost of iteration______300______0.0025645257286439583 
cost of iteration______400______0.058015188756586206 train_accuracy------------ 0.9845559845559846

Вы видели разницу в точности между ними? Мы использовали те же параметры инициализации, ту же скорость обучения и то же количество итераций; отличается только оптимизатор, но посмотрите на результат!

Mini-batch accuracy : 0.8494208494208494
momemtum accuracy   : 0.8725868725868726
Rms accuracy        : 0.9613899613899614
adam accuracy       : 0.9845559845559846

Графическая визуализация модели

Вы можете обратиться в репозиторий, если у вас есть сомнения по поводу кода.

Резюме

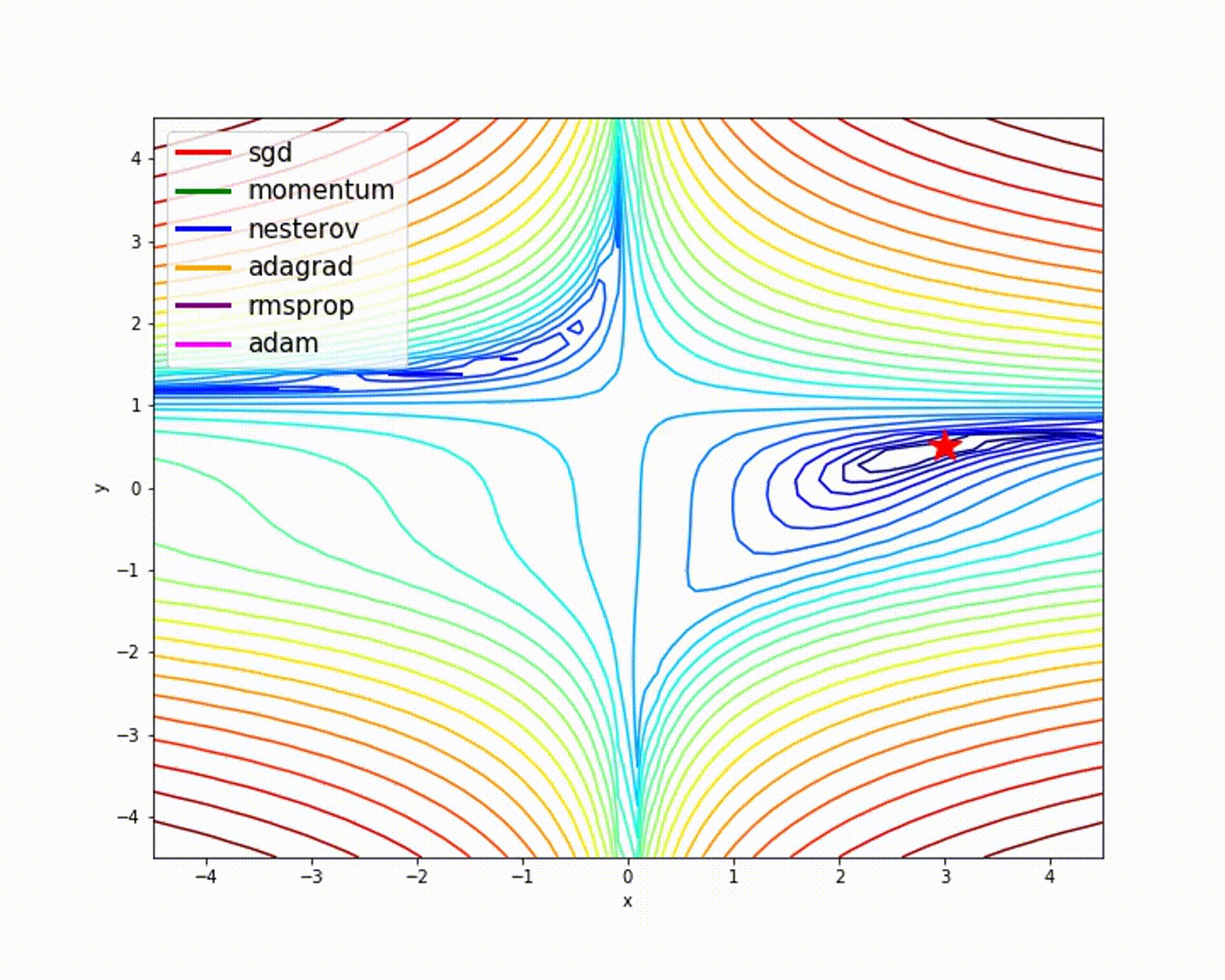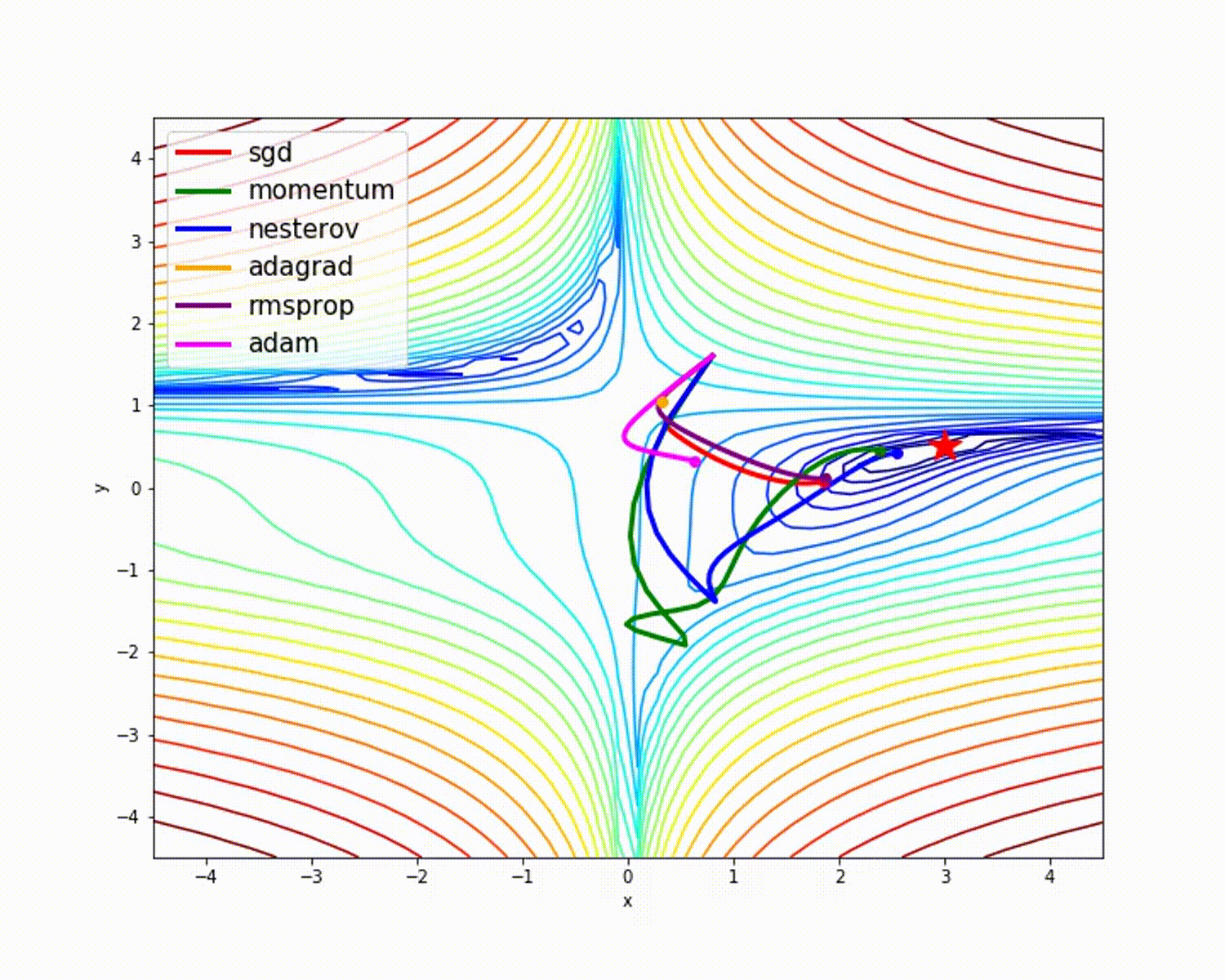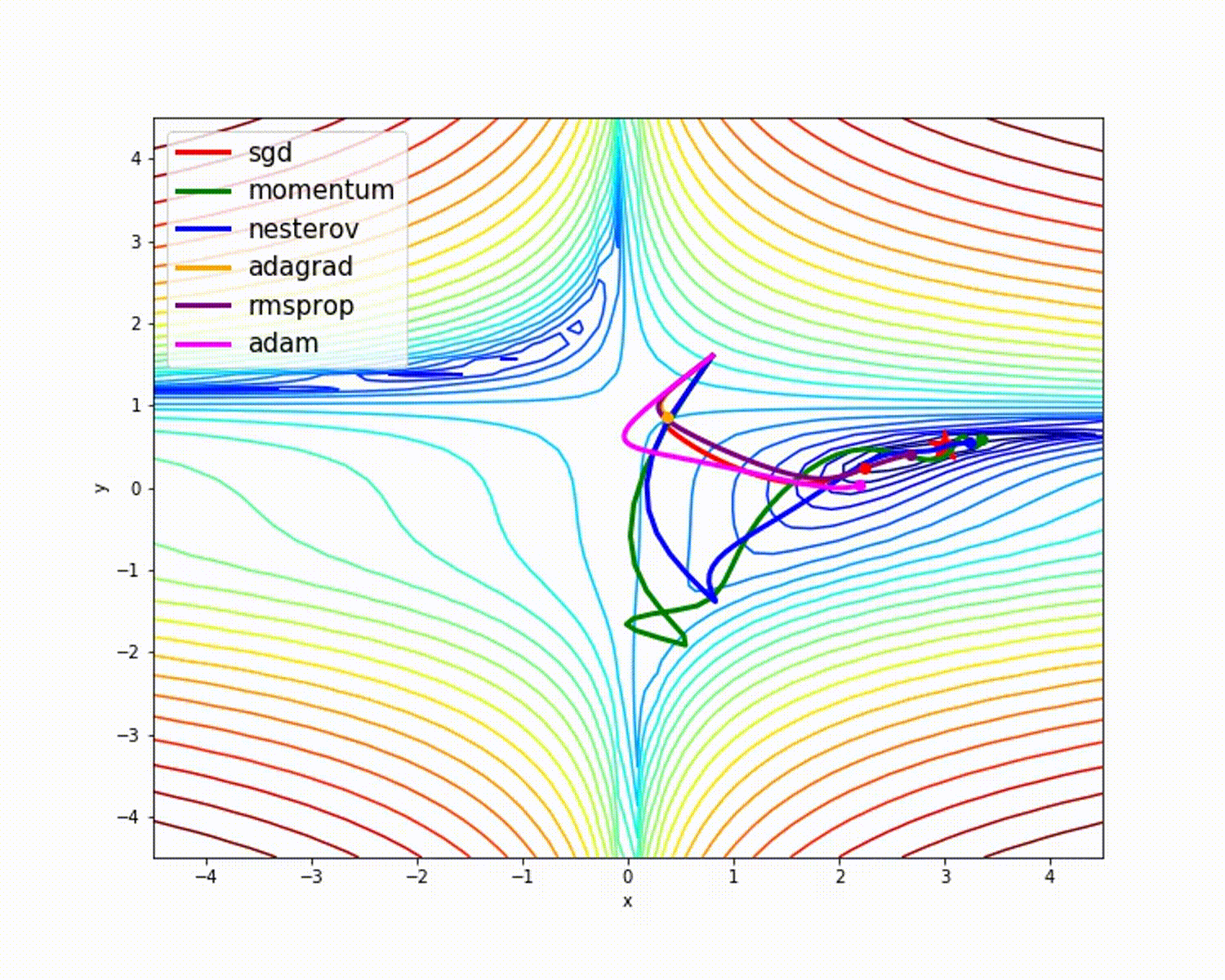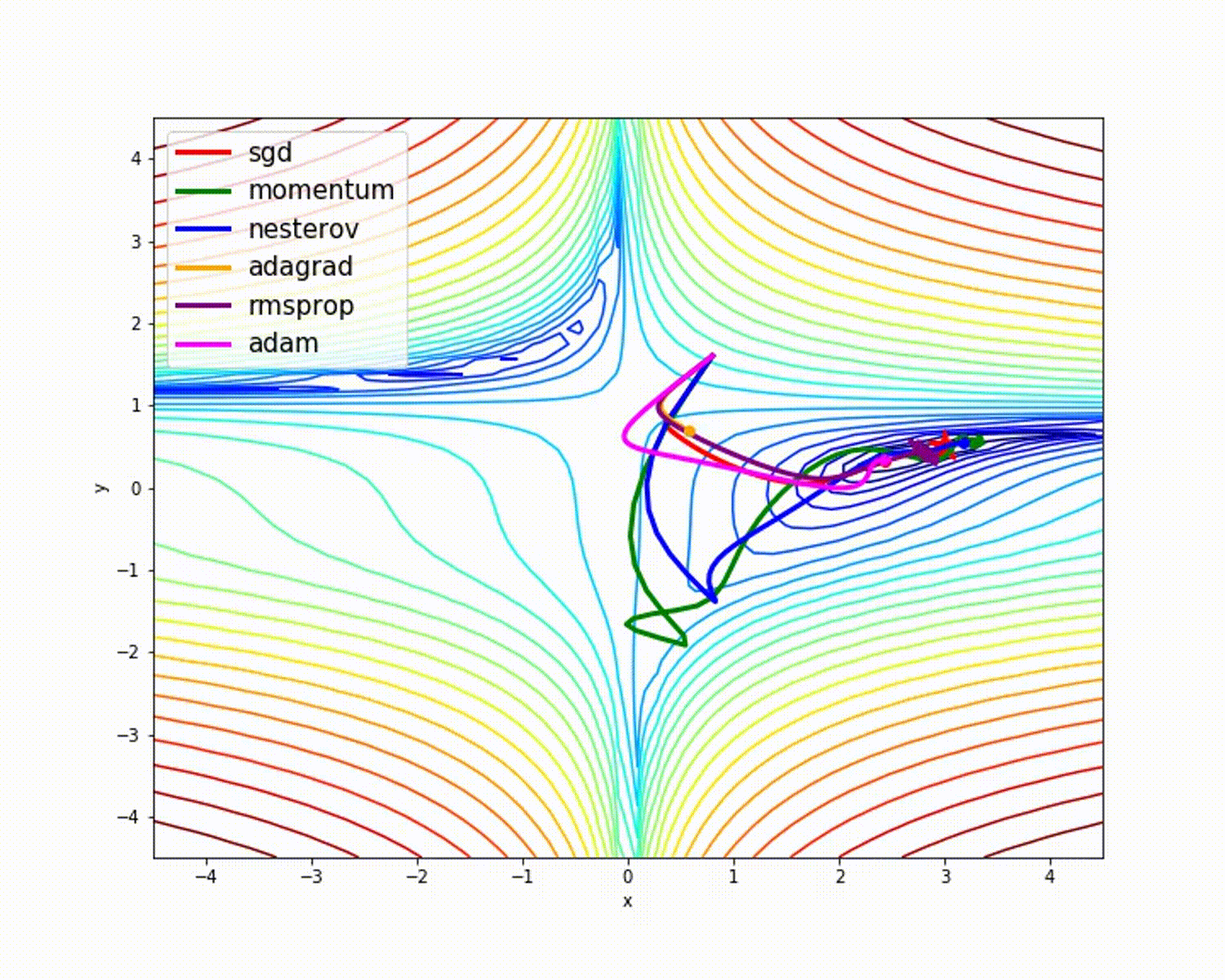
источник
Как мы уже видели, оптимизатор Adam дает хорошую точность по сравнению с другими оптимизаторами. На рисунке выше видно, как модель учится на итерациях. Momentum дает скорость SGD, а RMSProp дает экспоненциальное среднее значение веса для обновленных параметров. Мы использовали меньше данных в приведенной выше модели, но мы увидим больше преимуществ оптимизаторов при работе с большими наборами данных и многими итерациями. Мы обсудили основную идею оптимизаторов, и я надеюсь, что это даст вам некоторую мотивацию узнать больше об оптимизаторах и использовать их!

Ресурсы

Курс по Coursera — это даст более детальное представление о глубоком обучении
Алгоритм оптимизации — основы оптимизации

Перспективы нейронных сетей и глубокого машинного обучения просто огромны, и по самым скромным оценкам, их влияние на мир будет примерно таким же, как влияние электричества на промышленность в XIX веке. Те специалисты, которые оценят эти перспективы раньше всех, имеют все шансы стать во главе прогресса. Для таких людей мы сделали промокод HABR, который дает дополнительные 10% к скидке на обучение, указанной на баннере.

Eще курсы