Комментарии 32
Колышек ничего не даёт, так как к нему можно подойти с двух сторон.
Кончное множество колышков тоже ничего не даёт, по тем же соображениям.
Довольно легко доказать, что конечным количеством колышков не обойдётесь (см. выпуклость между колышками – в какую она сторону?)
У вас там какие-нибудь заморочки вроде петли, скользящей по верёвке, есть?
Кажется, пришло время раскрывать карты. Хоть поймём, чем различается наше понимание задачи.
Полагаю, инь-янь нам в помощь ))))
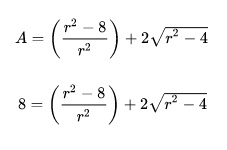
Спасибо, люблю такие песочницы, где можно играясь условиями много разных задачек получить.
Странно, что к этой задаче не подключились физики.
Какую часть ракеты выщипает коза если она летит со скоростью 0.99с относительно наблюдателя и относительно космонавта?
Какую часть наночастиц выщипает волновой пакет нанокоз?
И тд
Математически у числа пи известна вся бесконечность знаков, поэтому вычисления с использованием констант математически точные. С арккосинусом проблема в том, что точных аналитических представлений для решения уравнения вида 0=f(x)+g(trig(x)) где trig(x) — любая (ЕМНИП реально любая) тригонометрическая функция, не существует.
Как поступают математики, когда решение невозможно выразить через элементарные функции? Очень просто: придумывают специальную функцию, значение которой по определению равно требуемому.
Например, exp(a*x)+exp(b*x)=1, найти x, где a, b — параметры (произвольные действительные числа)
Для некоторых уравнений, которые не решаются, придумали специальные функции. Например, если y = x*exp(x) — то x=W(y) — функция Ламберта. С её помощью можно точно решить некоторые трансцендентные уравнения или хотя бы выразить решение в терминах специальных функций.
Аналогично y=sin(x)/x, обращения в элементарных функциях не существует.
Мы можем представить область как один сектор круга радиуса r плюс два правильных треугольника, а затем для получения формулы воспользоваться геометрическими навыками из курса средней школы.
"правильный треугольник" = равносторонний, а там явно не так, там прямоугольный треугольник.
Ноги растут из кривого перевода:
"right triangle" = прямоугольный треугольник, а не "правильный треугольник".
Как решать «упрямые» уравнения?