Вертел я ваши UIView

Эта статья является логическим продолжением UIKit ты вообще про UI?
Если вы ее пропустили, рекомендую сначала ознакомиться с ней. На всякий случай напоминаю, что весь графический интерфейс – это ответственность слоев (не вью!).

Я люблю пользоваться инструментами разработки, когда они мне понятны: я знаю, какого результата ожидать и, главное, как получается нужный мне эффект. Безусловно можно просто запомнить ряд функций и параметров для них, которые будут давать нужный результат. Но хорошим разработчиком так не станешь.

Сегодня я не буду подробно разбирать проективную геометрию, глубокие математические обоснования и принципы работы с матрицами. Надеюсь, что вы либо уже знакомы с этим, либо можете разобраться в этом сами. Я постараюсь объяснить все так, чтобы было понятно даже тем, кто видит все эти ужасные слова впервые. 

Давайте разберемся, как работают трансформации, постараемся понять подходы к ним и найти закономерности. Для того, чтобы начать погружение в трансформации, стоит для начала разобраться с контекстом. Ведь мы не просто рисуем карандашом на листе бумаги, мы управляем объектами в виртуальном мире. Сделаю небольшую оговорку – на самом деле все это очень сложные технические процессы (шедевры инженерной мысли), разобраться в которых за 15 минут не получится. Поэтому я буду умышленно упрощать некоторые вещи для того, чтобы сформировать общее понимание.

1. Как устроен экран

Экран телефона (или любого другого устройства) – это реальное окошко в виртуальный мир. Физически экран представляет собой сетку из пикселей (большого-большого количества пикселей). Эта сетка – двумерную плоскость, у которой есть ограниченное количество пикселей по высоте и ширине.

Виртуальный мир трехмерный. Какими бы плоскими не были слои, которые мы создаем, размещаем мы их в трехмерном пространстве.

2. Немного геометрии

Все мы изучаем в школе Элементарную геометрию. Ее еще называют Евклидовой. И чаще всего это единственная геометрия, с которой мы знакомы. Поэтому пространство и фигуры в этом пространстве мы рассматриваем исключительно с этой точки зрения. Проблема в том, что, когда мы захотим, скажем, две пересекающиеся прямые спроектировать в другую плоскость, они могут оказаться параллельными.

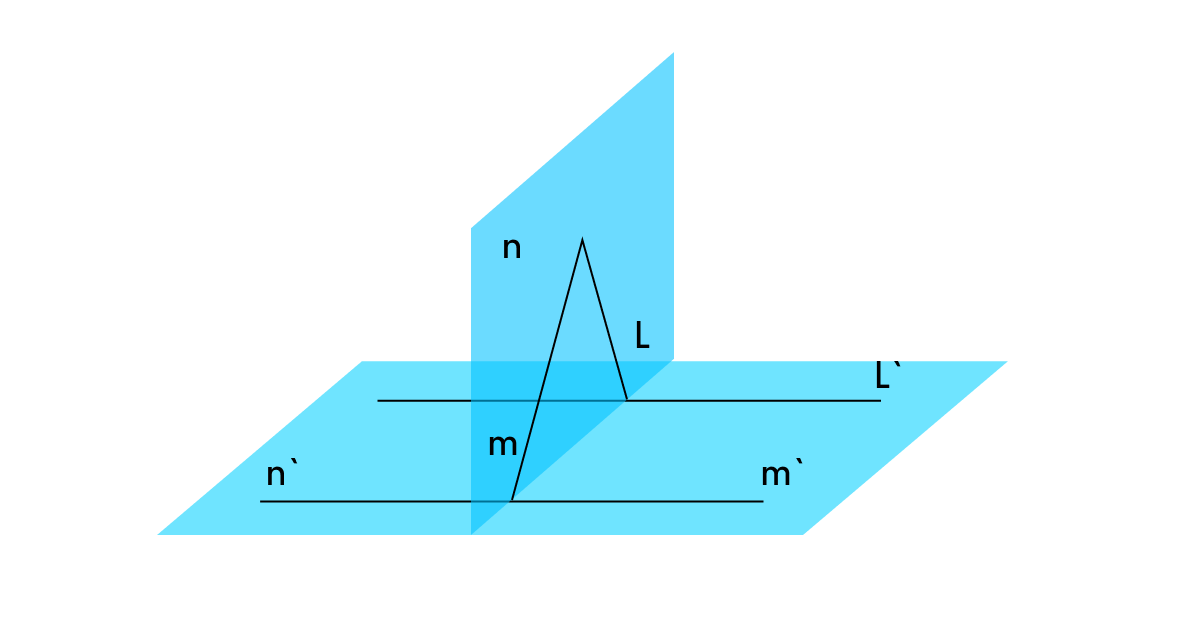
Для нашего интерфейса важно, чтобы при перемещении из одной плоскости в другую, объекты сохраняли свои свойства и консистентный внешний вид. Поэтому здесь используется Проективная геометрия. 

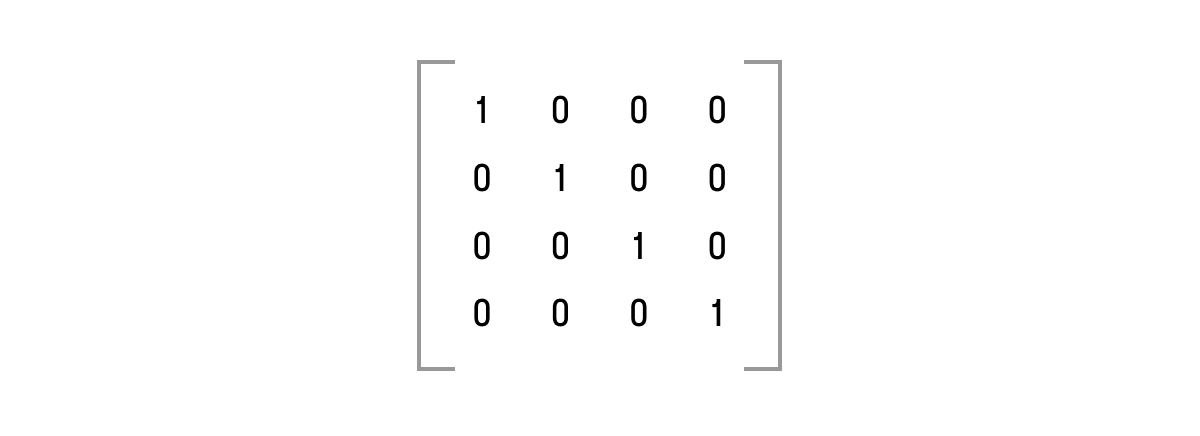
Вы наверняка видели вот такую запись (на матрицу пока не смотрим):

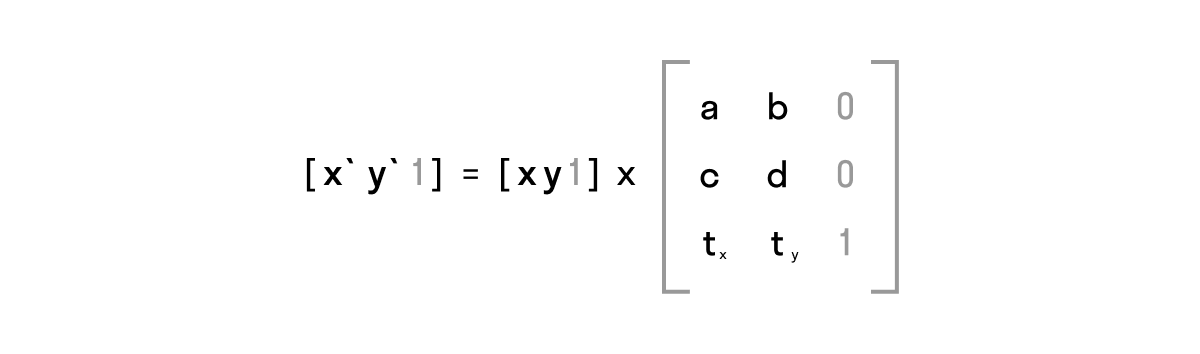
Координаты (x, y) нам понятны. Откуда берется 1? Дело в том, что если в Элементарной геометрии используется прямоугольная система координат (Декартова) (x, y), то в проективной – однородные координаты (xw, yw, w), где w – масштабный множитель, неравный 0. И когда мы хотим перевести координаты из однородных в двумерный вектор, делим каждую координату на множитель w:

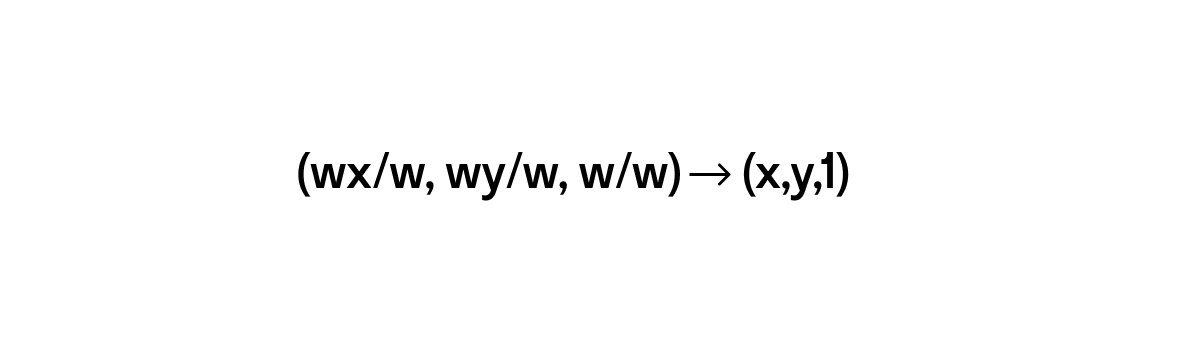
Если вам интересно, почему это именно так и как это объясняется математически, я предлагаю вам разобраться самостоятельно. А нам пока достаточно этого контекста.

3. Transforms

Думаю, сначала стоит разделить 2D и 3D трансформации. Несмотря на то, что UIView – строго двумерные объекты, мы в прошлый раз выяснили, что вью является всего лишь оберткой над слоями. А слои у нас живут уже в трехмерном пространстве. И вью предоставляет API для работы с трансформациями как в 2D, так и в 3D.

CALayer	UIView
setAffineTransform(_ m: CGAffineTransform)	transform
transform	transform3D

На всех примерах будем использовать API UIView, потому что оно удобнее. Но все то же самое справедливо, если мы будем работать напрямую со слоями.

3.1 2D Transforms

2D трансформации представлены аффинными преобразованиями и структурой CGAffineTransform, которая является матрицей 3х2. Как видно из префикса CG – они относятся к фреймворку Core Graphics. Важным критерием таких преобразований является сохранение коллинеарности точек (т.е. те стороны слоя, которые были параллельными до преобразования, останутся параллельными после него).

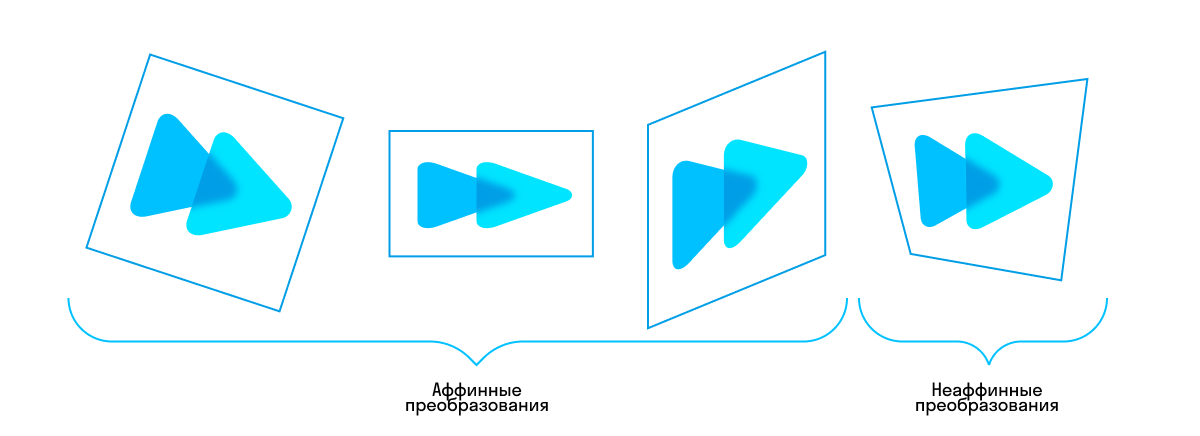
Аффинные преобразования происходят путем умножения вектора на матрицу 3x3 (вспоминаем однородные координаты). Что можно представить в виде системы уравнений, решением которого будут новые координаты для каждой точки.

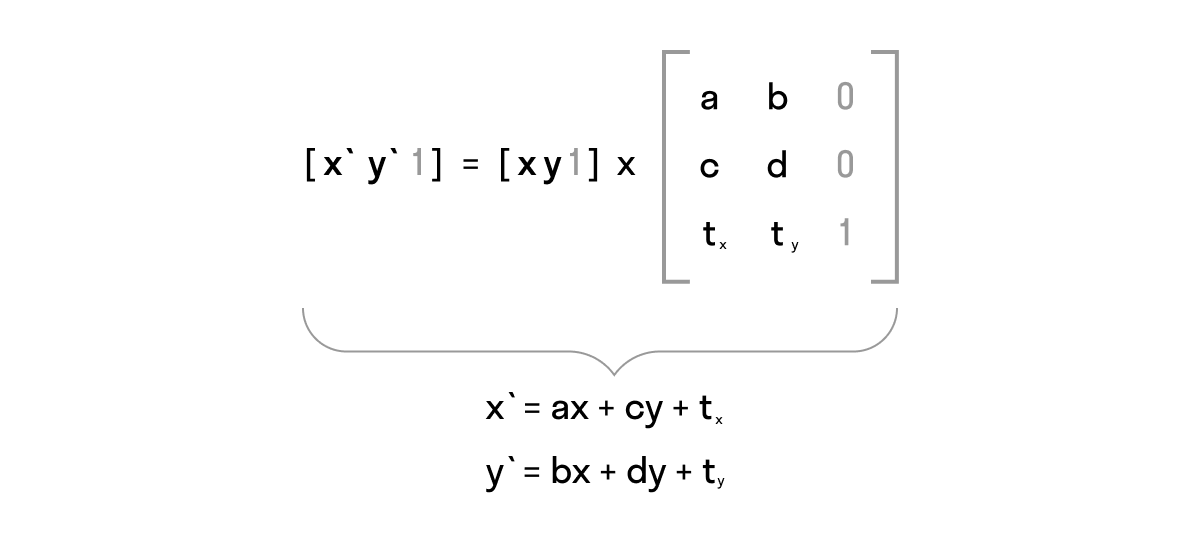
Если вы возьметесь сейчас проверять эти формулы и рассчитывать «на бумаге», как это работает, не забывайте про anchorPoint (по дефолту он в центре) и origin. Вообще это сложный механизм и, если просто хотите проверить вычисления, берите оба эти значения 0,0. 

Вот небольшая шпаргалка (имейте в виду, что anchorPoint перенесен в 0,0, для удобства восприятия).

Слой без преобразований имеет единичную матрицу и обозначается свойством CGAffineTransform.identity.

Давайте проверим вычисления этой матрицы в системе уравнений и увидим, что преобразованная точка равна исходной:

Перемещение:

Сверимся с нашей шпаргалкой и построим нужную матрицу с помощью CGAffineTransform

view.transform = CGAffineTransform(
  a: 1,
  b: 0,
  c: 0,
  d: 1,
  tx: 40,
  ty: 30
)

либо можем воспользоваться специальным инициализатором:

view.transform = CGAffineTransform(translationX: 40, y: 30)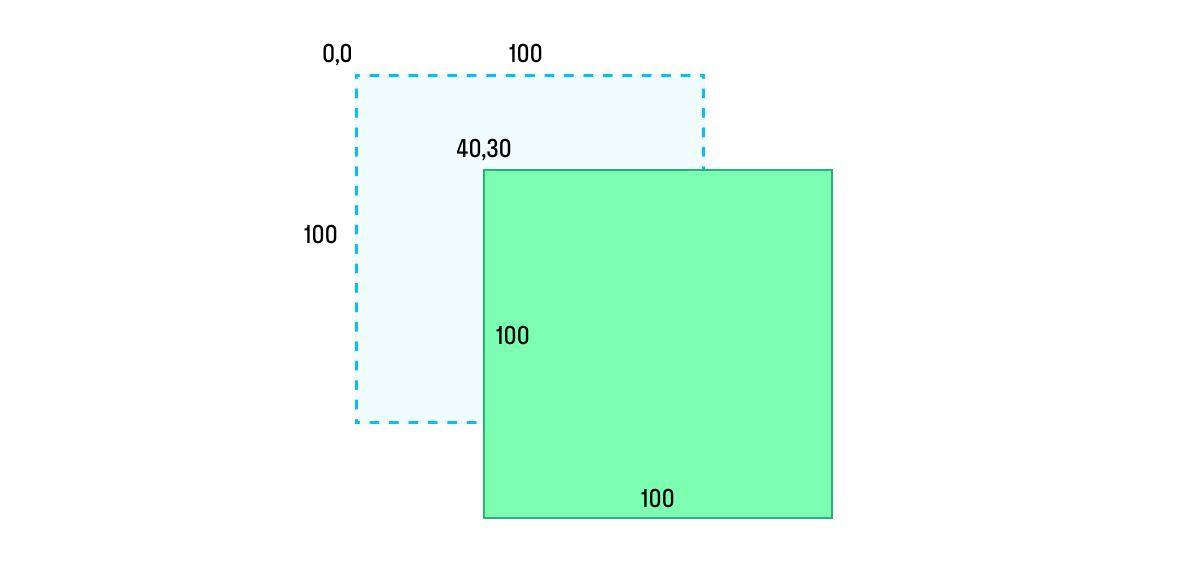

Вращение:

Строим матрицу:

view.transform = CGAffineTransform(
  a: cos(.pi / 4),
  b: -sin(.pi / 4),
  c: sin(.pi / 4),
  d: cos(.pi / 4),
  tx: 0,
  ty: 0
)

или:

view.transform = CGAffineTransform(rotationAngle: .pi / 4)

Масштабирование:

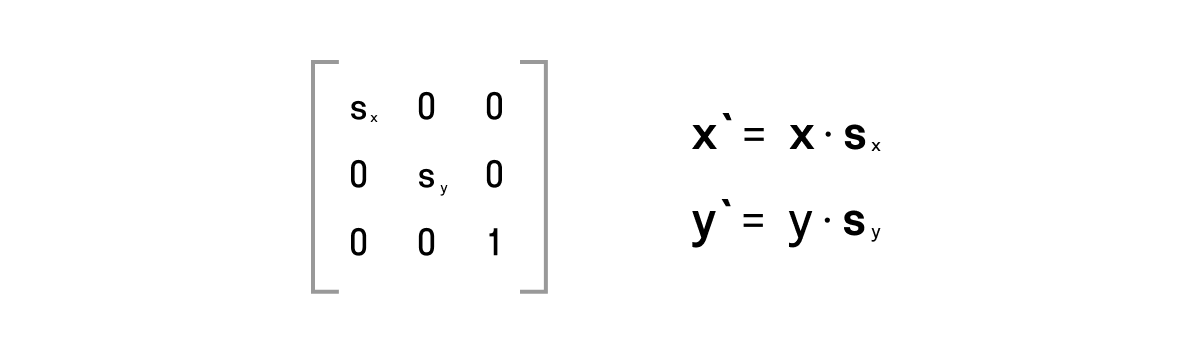
Строим матрицу:

view.transform = CGAffineTransform(
  a: 0.5,
  b: 0,
  c: 0,
  d: 0.5,
  tx: 0,
  ty: 0
)

или:

view.transform = CGAffineTransform(scaleX: 0.5, y: 0.5)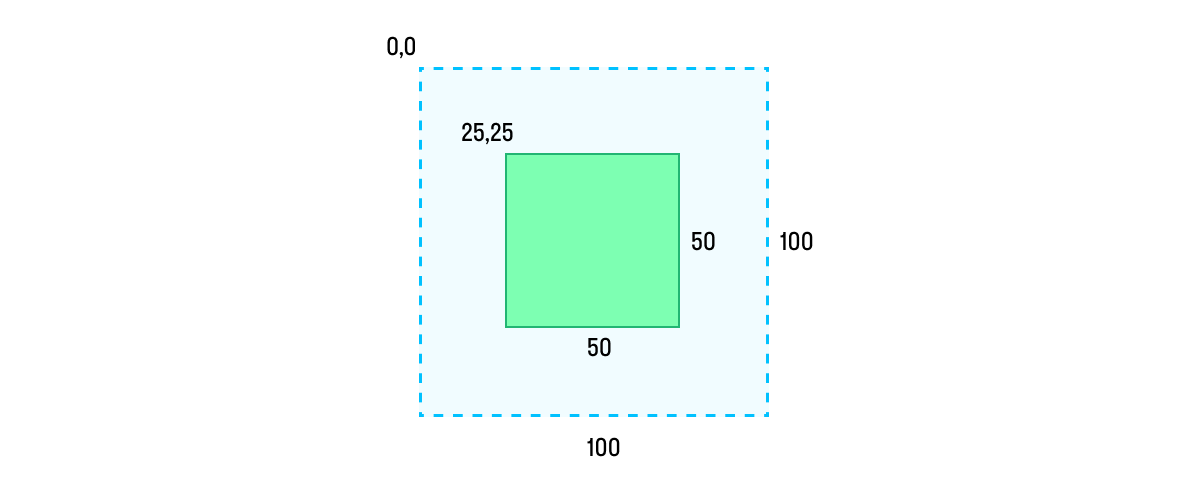

Сдвиг:
Для сдвига нет специального инициализатора, но мы можем просто, глядя на шпаргалку, построить матрицы:

view.transform = CGAffineTransform(
  a: 1,
  b: 0,
  c: tan(-.pi / 6),
  d: 1,
  tx: 0,
  ty: 0
) 
view.transform = CGAffineTransform(
  a: 1,
  b:  tan(.pi / 6),
  c: 0,
  d: 1,
  tx: 0,
  ty: 0
)

Для сдвига у нас нет специального инициализатора, но, понимая, как это работает и используя шпаргалку, мы можем написать расширение:

extension CGAffineTransform {
    init(shearXAngle: CGFloat) {
        self.init(
            a: 1,
            b: 0,
            c: tan(shearXAngle),
            d: 1,
            tx: 0,
            ty: 0
        )
    }
      init(shearYAngle: CGFloat) {
        self.init(
            a: 1,
            b: tan(shearYAngle),
            c: 0,
            d: 1,
            tx: 0,
            ty: 0
        )
    }
}

Теперь вызов для сдвига по оси X будет такой же простой, как и остальные:

view.transform = CGAffineTransform(shearXAngle: -.pi / 6)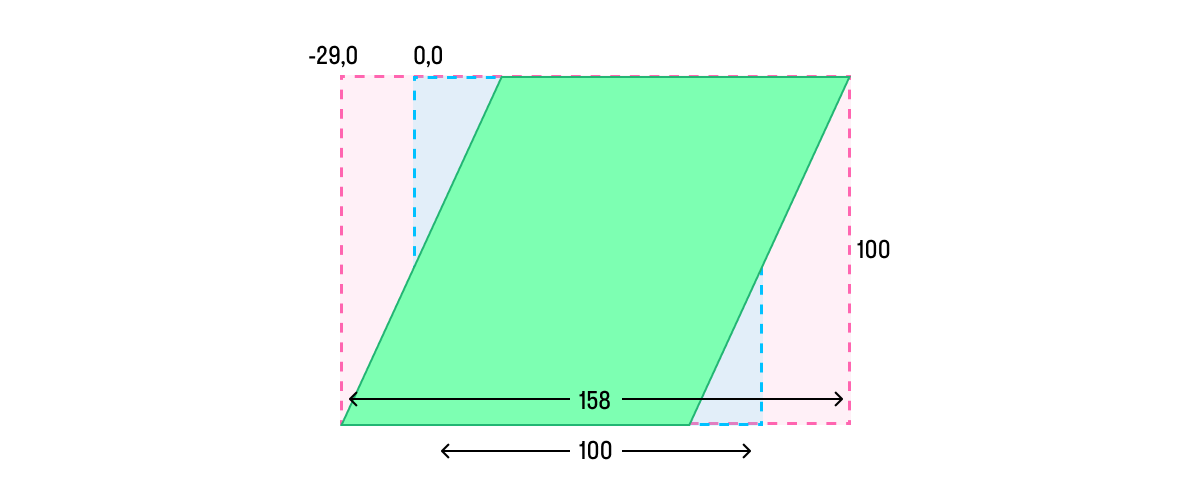

для сдвига по оси Y:

view.transform = CGAffineTransform(shearYAngle: .pi / 6)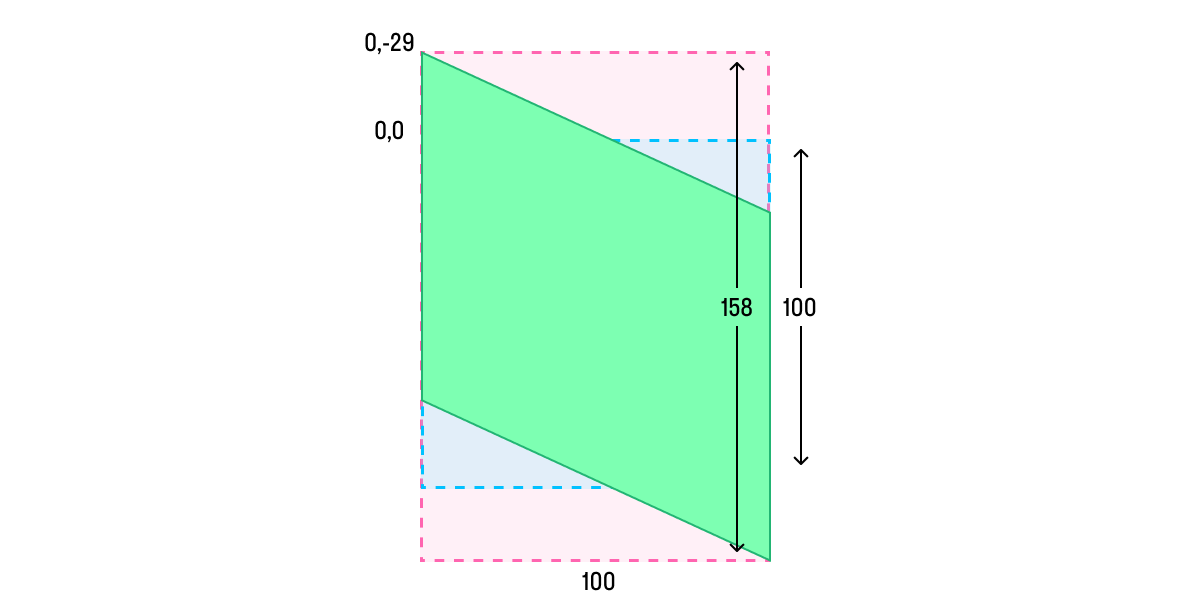

Еще мы можем комбинировать разные преобразования:

Все параметры, которые хотим изменить, мы можем указать в общем инициализаторе:

view.transform = CGAffineTransform(
  a: 0.5,
  b: 0,
  c: 0,
  d: 0.5,
  tx: 40,
  ty: 30
)

Но! Имейте в виду, что порядок применения преобразования очень важен. Матрица A Х Матрица B не всегда равно Матрица B Х Матрица A.

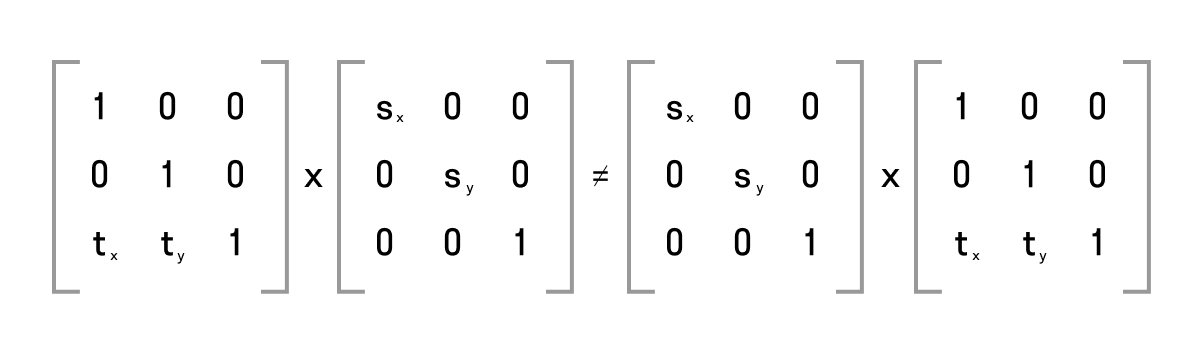
Поэтому обычно важно явно указывать порядок выполнения трансформации. Например:

var transform = CGAffineTransform.identity
transform = transform.translatedBy(x: 40, y: 30)
transform = transform.scaledBy(x: 0.5, y: 0.5)
view.transform = transform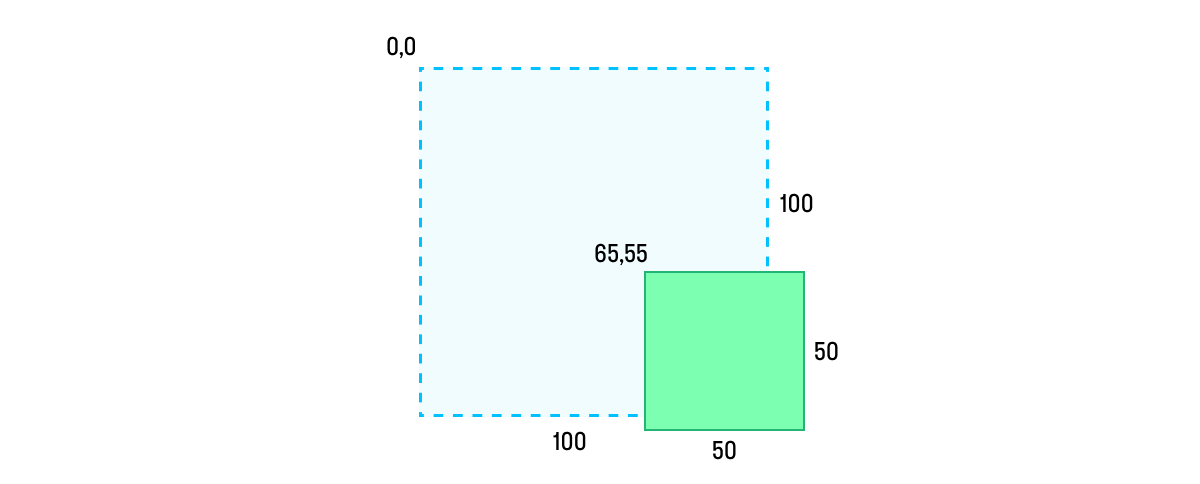

Результат не равен:

var transform = CGAffineTransform.identity
transform = transform.scaledBy(x: 0.5, y: 0.5)
transform = transform.translatedBy(x: 40, y: 30)
view.transform = transform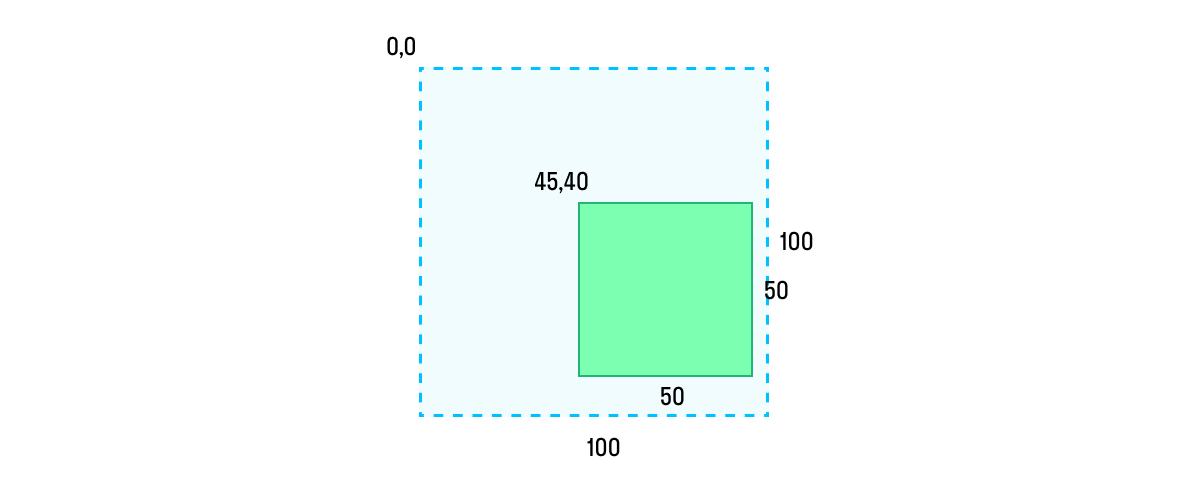

Так происходит, потому что, если мы сначала перемещаем слой, то его position (а вместе с ним и anchorPoint) меняет свое положение. Соответственно сжатие происходит уже вокруг другой точки.

3.2 3D Transforms

3.2.1 Вращение

Мы уже знаем, что виртуальный мир трехмерный. Соответственно и объекты мы можем «вертеть» относительно трех осей (X, Y, Z).

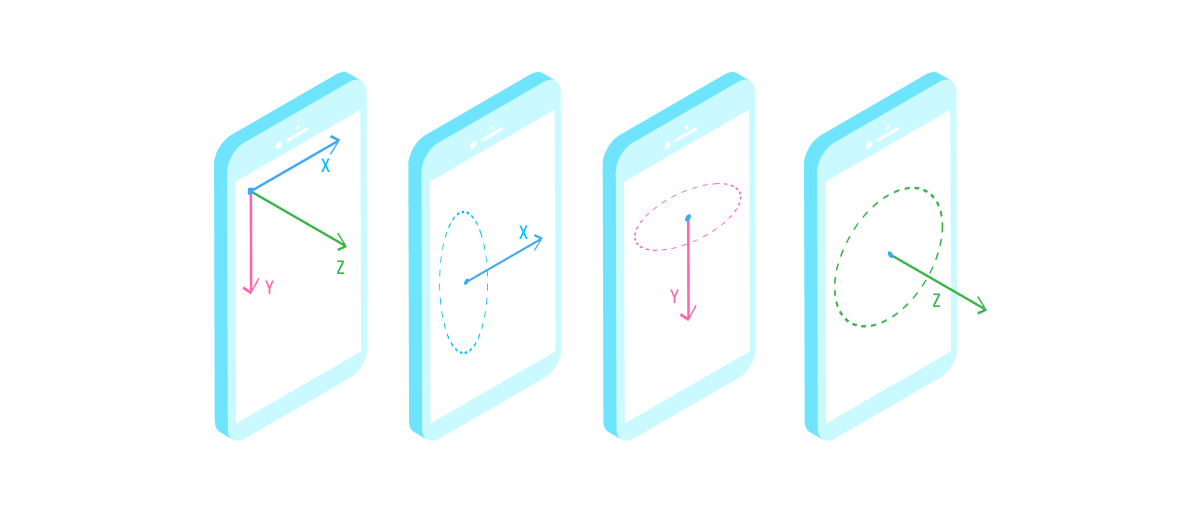
Как вы видите, вращение относительно оси Z аналогично вращению объекта с помощью аффинного преобразования.

А вот вращения объектов вокруг осей X и Y выходят за пределы двухмерного пространства. Когда объект вращается в реальном мире, мы ожидаем, что тот край, который удаляется от нас, становится меньше (эффект перспективы).

Для того, чтобы работать с трехмерными трансформациями, нам предоставлена структура CATransform3D, которая является матрицей 4х4. Подобно работе с 2D трансформациями (аффинными преобразованиями), 3D осуществляются путем умножения вектора на матрицу. Только в этом случае успользуются 3 координаты вектора и матрица 4х4.

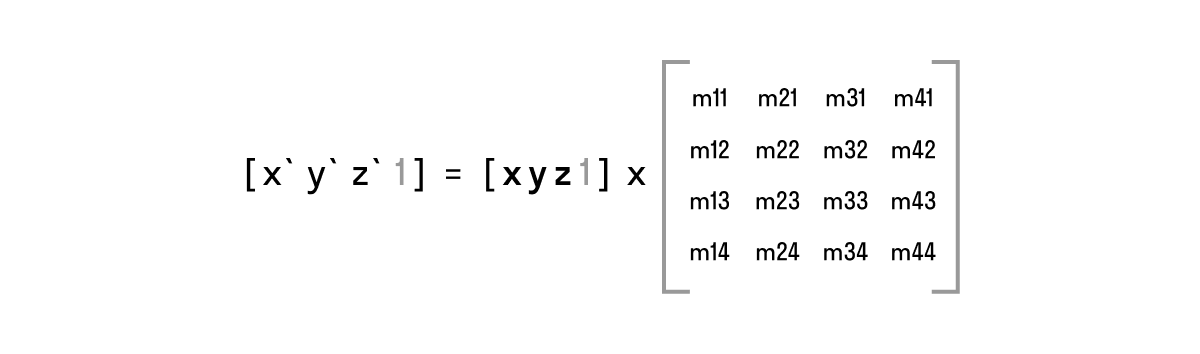
CATransform3DIdentity – глобальная константа, обозначающая матрицу без преобразований.

Небольшая шпаргалка для вращения объектов в 3D:

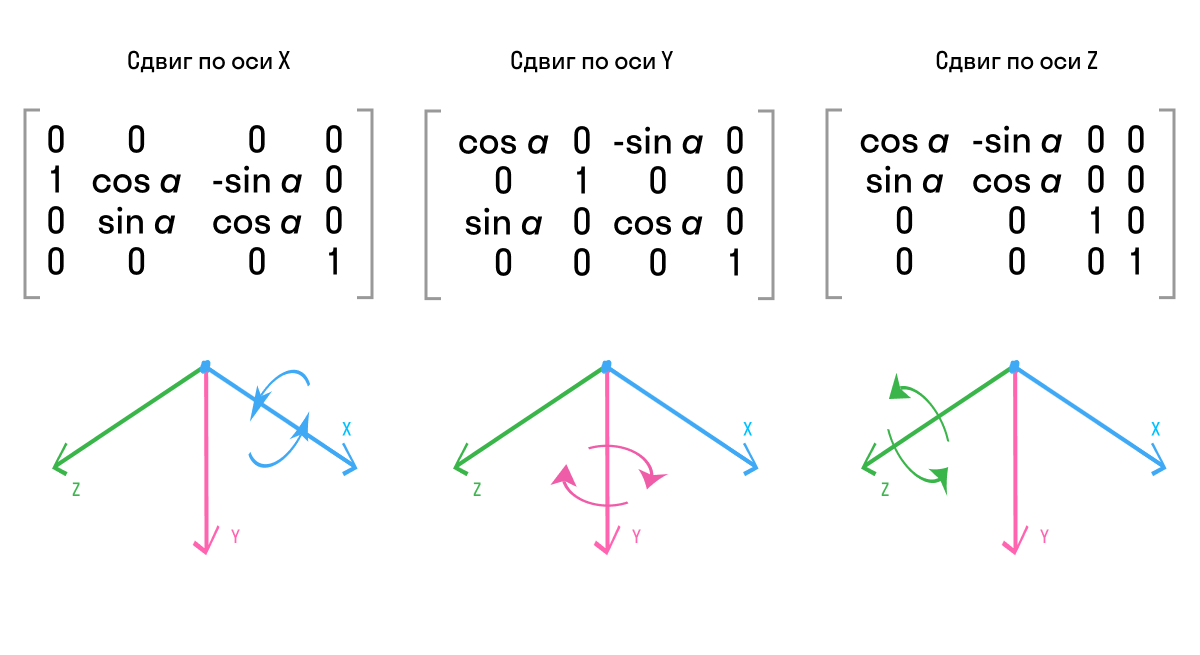
Давайте попробуем повернуть слой на 45° по оси Y. В случае с аффинными преобразованиями мы указывали только угол. Здесь же мы должны явно указать, по какой оси хотим получить вращение (x, y, z – в таком порядке аргументы и расположены). Если мы передаем 0, вращения относительно соответствующей оси не происходит. Любое другое значение приведет к повороту слоя на заданный угол. Причем числовое значение абсолютно не важно. Это не коэффициент, поэтому можно использовать любое отличное от 0 (0.01 и 100 дадут одинаковый результат). Но важен знак параметра, он управляет направлением поворота (0.01 и -0.01 повернут слой в противоположных направлениях). Несмотря на это, для общей консистентности и чтобы не создавать дополнительную когнитивную нагрузку, принято задавать эти параметры единицей, а направление поворота – знаком самого угла.

view.transform3D = CATransform3DMakeRotation(.pi / 4, 0, 1, 0)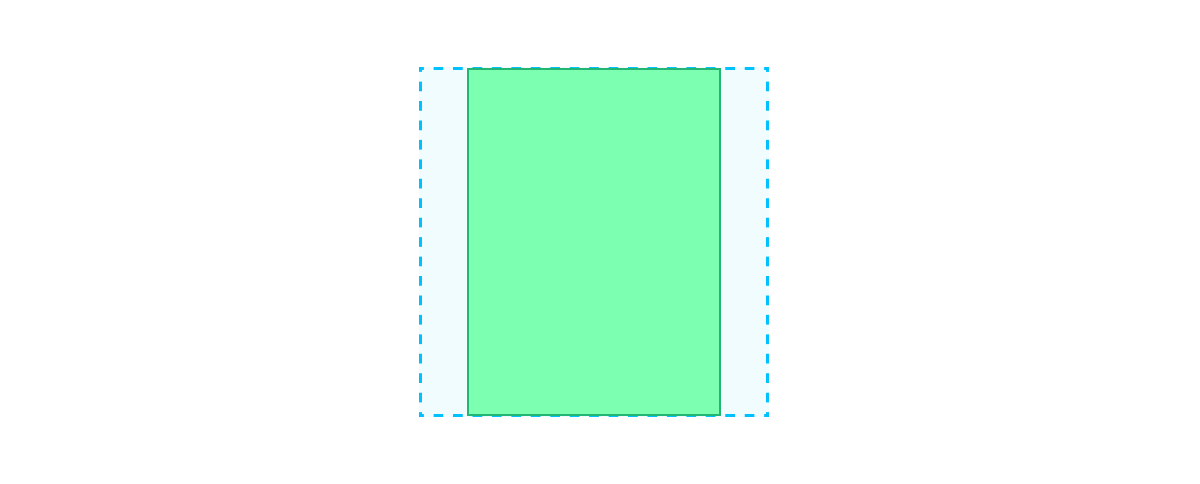

Выглядит, как сжатие. Дело в том, что по дефолту эффект перспективы не установлен. Более того, у нас нет простого и понятного API для этого. Когда мы хотим, чтобы объект или его часть меняли свой размер по мере приближения или удаления, нам нужно поменять один параметр матрицы.

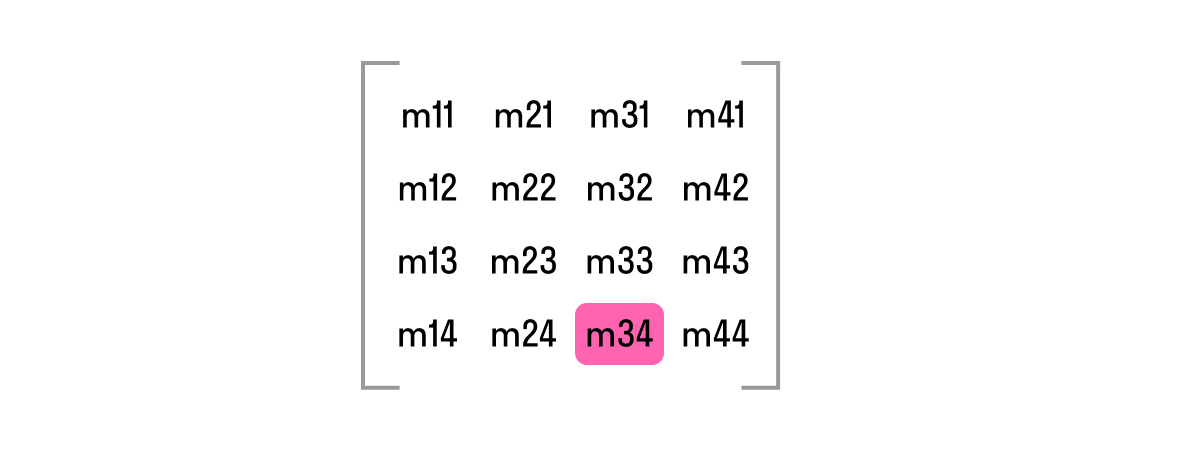
В реальном мире перспектива находится в центре и все объекты по мере удаления от нас будут стремиться к этому центру, превращаясь в точку.

Для большей реалистичности интерфейса будем придерживаться того же правила, поэтому значение будет иметь отрицательный знак (положительные значения по оси Z направлены в сторону камеры) и вычисляться по формуле -1 / value. Значения делителя подбирались эмпирическим путем и считаются оптимальными в диапазоне от 300 до 1000.

var transform3D = CATransform3DIdentity
transform3D.m34 = -1 / 500
view.layer.sublayerTransform = transform3D
        
view.transform3D = CATransform3DRotate(transform3D, .pi / 3, 0, 1, 0)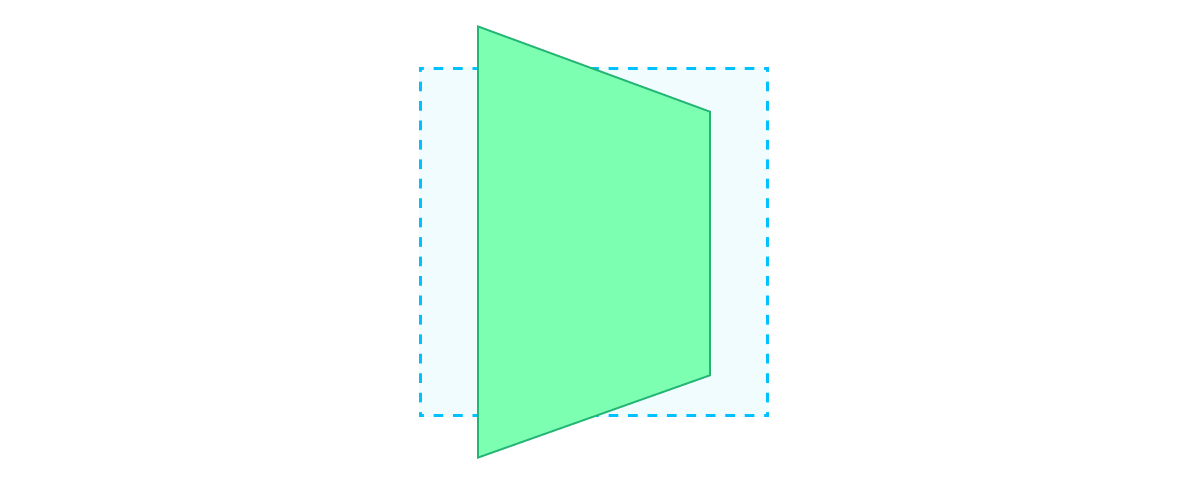

Да, для каждой трансформации этот параметр задается отдельно, но если мы хотим, чтобы все наши слои имели одинаковую перспективу, мы можем задать ее для родительского слоя, в котором они находятся с помощью свойства sublayerTransform. В этом случае точка перспективы будет находиться в центре того слоя, для которого вы устанавливаете этот параметр, как и в реальном мире.

var transform3D = CATransform3DIdentity
transform3D.m34 = -1 / 500
view.layer.sublayerTransform = transform3D
 
leftView.transform3D = CATransform3DMakeRotation(.pi / 3, 0, 1, 0)
rightView.transform3D = CATransform3DMakeRotation(-.pi / 3, 0, 1, 0)

Думаю многие хоть раз задавались вопросом, а что там на другой стороне вью. Это не сложно проверить. Достаточно развернуть ее на 180° и мы увидим развернутый слой.

Получается, что при отрисовке нашего слоя производятся вычисления сразу и для обратной стороны. Звучит неэффективно. Если мы не собираемся никогда заглядывать на обратную сторону слоев, то и считать их не нужно. У слоев есть для этого специальное свойство isDoubleSided. Это булевое свойство, которое управляет вычислениями обратной стороны слоев. По дефолту true. Так что, если вам никогда не будет нужно переворачивать свой слой и вы хотите прироста производительности, выставляйте isDoubleSided значение false.

3.2.2 Перемещение и Масштабирование

Вращение:

public func CATransform3DMakeRotation(_ angle: CGFloat, _ x: CGFloat, _ y: CGFloat, _ z: CGFloat) -> CATransform3D
public func CATransform3DRotate(_ t: CATransform3D, _ angle: CGFloat, _ x: CGFloat, _ y: CGFloat, _ z: CGFloat) -> CATransform3D

Перемещение:

public func CATransform3DMakeTranslation(_ tx: CGFloat, _ ty: CGFloat, _ tz: CGFloat) -> CATransform3D
public func CATransform3DTranslate(_ t: CATransform3D, _ tx: CGFloat, _ ty: CGFloat, _ tz: CGFloat) -> CATransform3D

Масштабирование:

public func CATransform3DMakeScale(_ sx: CGFloat, _ sy: CGFloat, _ sz: CGFloat) -> CATransform3D
public func CATransform3DScale(_ t: CATransform3D, _ sx: CGFloat, _ sy: CGFloat, _ sz: CGFloat) -> CATransform3D

Мы видим, что для всех трансформаций у нас есть по 2 метода. Один принимает только параметры для матрицы, а второй дополнительно объект CATransform3D. Во-первых, как мы уже выяснили, с помощью дополнительного объекта мы задаем эффект перспективы. Во-вторых, мы можем комбинировать разные трансформации.

Перемещение и масштабирование рассмотрим вкратце. Сами по себе они вряд ли могут быть полезными. Масштабировать объект по оси Z, который не имеет глубины, не представляется возможным. Поэтому эффективнее использовать аффинные преобразования. Перемещения объекта по осям X и Y эквивалентно перемещению с помощью аффинных преобразований, а вот по оси Z эффект будет аналогичен скейлу при помощи все тех же аффинных преобразований. Кстати, для того, чтобы с помощью перемещения по оси Z объект увеличился/уменьшился в 2 раза, значение нужно задавать равное делителю, который используем для установки коэффициента перспективы (m34).

Вообще API для работы с этими трансформациями может показаться достаточно странным на первый взгляд. На самом деле оно не многим сложнее работы с CGAffineTransform. Есть даже возможность приведения CATransform3D к CGAffineTransform. Зачем это нужно? Производить вычисления с матрицами 3х3 проще, чем 4х4. Поэтому, если хотите прирост в производительности, все трансформации, которые возможно, приводите к аффинным.

let transform3D = CATransform3DMakeTranslation(100, 100, 0)
if CATransform3DIsAffine(transform3D) {
     view.transform = CATransform3DGetAffineTransform(transform3D)
} else {
     view.transform3D = transform3D
}

Важный момент! CATransform3DIsAffine проверяет использует ли трансформация параметр для оси Z (true вернется только в том случае, когда значение z == 0). Так что имейте в виду, что, несмотря на визуальную схожесть перемещения объекта по оси Z и обычный 2D скейл, вы не сможете представить такую трансформацию в виде аффинных преобразований.

3.2.3 zPosition & anchorPointZ

zPosition – это просто координата на оси Z. В отличие от x и y при перемещении с помощью трансформации она не меняется. С помощью этого свойства также можно управлять положением слоя. Но не забывайте про коэффициент перспективы у родительского слоя sublayerTransform. В противном случае вы просто будете менять положение текущего слоя в иерархии отображения. Напоминаю, что на респондер чейн это никак не влияет.

anchorPointZ – это тоже координата на оси Z. По дефолту ее значение 0.  Вокруг этой координаты (аналогично anchorPoint) происходят трансформации в трехмерном пространстве. Когда мы задаем это свойство, фактически  меняется положение слоя на оси Z и, если установлена перспектива, мы это увидим, как в случае с zPosition. Но! Положительные значения направлены в обратном направлении (anchorPointZ == -zPosition). Когда мы меняем anchorPoint, то position сдвигаем в противоположную сторону. Для anchorPointZ и zPosition устанавливаются одинаковые значения.

Еще один важный момент: если в случае с anchorPoint менялось значение position, то при изменении anchorPointZ значение zPosition остается прежним (как и при трансформациях).
С помощью этого свойства и анимаций можно реализовывать интересные интерфейсные решения.

Вывод

Вот мы и разобрали все основные возможности работы с базовым классом CALayer. Есть и другие виды слоев, выполняющие специализированные функции, но их стоит разбирать отдельно.

Тема с трансформациями кажется не самой простой. Как правило у нас есть есть стек инструментов, которыми мы периодически пользуемся, примерно зная, как это работает. За остальным лезем на StackOverFlow. Надеюсь мне удалось систематизировать подход к трансформациям и вам было интересно это читать. А также, теперь вы будете охотнее использовать это на практике.

Теперь можно смело приступать к анимациям и создавать крутые интерфейсы.