Многие документы содержат защитные элементы, такие как голограммы, водяные знаки, гильош и т.д. В процессе сканирования таких документов возникает проблема — защитные элементы мешают системам распознавания (OCR). При разработке Smart PassportReader мы провели исследование, направленное на поиск и устранение подобных защитных элементов с изображений документов.


В нашей предыдущей статье по этой теме мы рассказали о первой половине решения задачи поиска — детектировании, т.е. определении наличия периодических элементов на изображении. Сегодня мы расскажем, как найти непосредственное положение периодических элементов на изображении, при условии, что детектирование прошло успешно: мы уверены, что элементы на изображении присутствуют. Вторая часть сильно зависит от первой, поэтому настоятельно рекомендуется сначала ознакомиться с первой, если вы этого еще не сделали.
Как и в прошлый раз, для этого будет использоваться преобразование Фурье.
Как и в прошлый раз, многие рассуждения будут показаны для одномерного случая, который потом легко переносится на двумерный.
Напомним, что) — исходное изображение длины
— исходное изображение длины  , состоящее из двух других: фонового изображения
, состоящее из двух других: фонового изображения ) и изображения
и изображения ) , содержащего периодический шаблон. Изображение
, содержащего периодический шаблон. Изображение ) , в свою очередь, мы представили сверткой (convolution) одного экземпляра шаблона
, в свою очередь, мы представили сверткой (convolution) одного экземпляра шаблона ) с гребнем Дирака
с гребнем Дирака ) :
:
%20%3D%20h(x)%20%2B%20g(x)%20%3D%20h(x)%20%2B%20f(x)%20%5Cast%20c(x))
Так как нам заранее известна структура периодического шаблона (в случае паспорта РФ — размер и период голограмм), для восстановления положения элементов достаточно знать только сдвиг всего шаблона по горизонтали и вертикали, что есть то же самое, что сдвиг одного из “орлов”.
Сдвиг сигнала паттерна) равносилен сдвигу импульсной функции
равносилен сдвигу импульсной функции ) , который приводит к измененной форме
, который приводит к измененной форме ) . Спектр преобразования Фурье сдвинутого сигнала изменяется только в фазе, оставляя неизменной амплитуду, позволяя, тем самым детектировать периодические паттерны вне независимости от их начального сдвига. Как важное следствие, вся полезная фазовая информация сосредоточена в тех же самых ДПФ позициях (частотах), что и пики амплитуды импульсного сигнала.
. Спектр преобразования Фурье сдвинутого сигнала изменяется только в фазе, оставляя неизменной амплитуду, позволяя, тем самым детектировать периодические паттерны вне независимости от их начального сдвига. Как важное следствие, вся полезная фазовая информация сосредоточена в тех же самых ДПФ позициях (частотах), что и пики амплитуды импульсного сигнала.
Предположим, что) сдвинут вправо на
сдвинут вправо на  , тогда:
, тогда:
%20%3D%20%5Cmathcal%7BF%7D_k%20c(x)%20%5Ccdot%20e%5E%7Bi%20%5CPhi_k%7D%2C)

Поскольку фазовый угол) для несмещенного
для несмещенного ) равен нулю, для смещенного
равен нулю, для смещенного ) он становится равным
он становится равным  . Для получения фазового сдвига
. Для получения фазового сдвига ) нам необходимо добавить каждый член
нам необходимо добавить каждый член  к соответствующему фазовому углу в
к соответствующему фазовому углу в ) для каждого
для каждого  . Заметим, что любой фазовый угол всегда берется по модулю
. Заметим, что любой фазовый угол всегда берется по модулю  и ограничивается интервалом
и ограничивается интервалом ) .
.
Фазовый сдвиг на в частотной области представляет сдвиг
в частотной области представляет сдвиг  во временной области, но
во временной области, но ) имеет период
имеет период  , поэтому мы может избежать избыточности рассмотрением лишь
, поэтому мы может избежать избыточности рассмотрением лишь  , обеспечив таким образом
, обеспечив таким образом  . Для удобства, пусть
. Для удобства, пусть  – это фазовый сдвиг, у которого
– это фазовый сдвиг, у которого  соответствует временному сдвигу на
соответствует временному сдвигу на  , а также пусть
, а также пусть  – это фазовый угол на
– это фазовый угол на  'ом амплитудном пике:
'ом амплитудном пике:

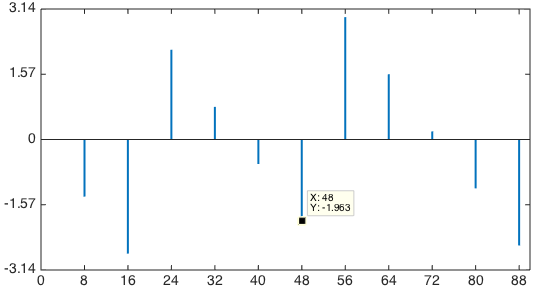
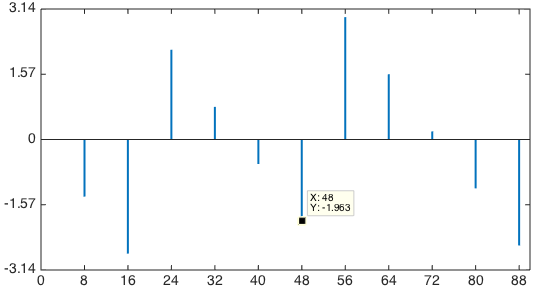
На рисунке показан пример ДПФ фазы сдвинутого импульсного сигнала с значениями , периодом
, периодом  и сдвигом
и сдвигом  . Например,
. Например,  и
и %20%5Ccdot%206%20%5Capprox%20-1%2C963) .
.
А вот так выглядит амплитуда и фаза ДПФ для похожей на шахматную доску сетки Гауссиан:
 — ДПФ -->
— ДПФ --> 

Для двумерного изображения, фазовый сдвиг теперь состоит из двух компонент
теперь состоит из двух компонент ) . Введем координатную сетку для ДПФ шахматоподобной системы пиков, показанных на втором и третьем рисунках выше, такую, что центральный пик имеет координаты
. Введем координатную сетку для ДПФ шахматоподобной системы пиков, показанных на втором и третьем рисунках выше, такую, что центральный пик имеет координаты ) , пики справа вверху
, пики справа вверху ) ,
, ) и так далее; ближайший диагональный пик имеет координаты
и так далее; ближайший диагональный пик имеет координаты ) . В общем случае, пик
. В общем случае, пик ) присутствует тогда и только тогда, когда
присутствует тогда и только тогда, когда ) – четно.
– четно.
Применяя вновь теорему о ДПФ сдвинутого сигнала, можно расширить уравнение сдвига и показать, что фазовый угол на
на ) пике для двумерного импульсного сигнала равен:
пике для двумерного импульсного сигнала равен:

Как и для одномерного случая, для получения сдвинутой фазы) необходимо добавить
необходимо добавить  к соответствующей фазе
к соответствующей фазе ) .
.
Для определения точного местоположения периодического паттерна достаточно оценить его фазовый сдвиг) , поскольку его пиксельная периодическая структура заранее известна. Пиксельный сдвиг
, поскольку его пиксельная периодическая структура заранее известна. Пиксельный сдвиг ) , впоследствии, нетрудно восстановить по информации о фазовом сдвиге.
, впоследствии, нетрудно восстановить по информации о фазовом сдвиге.
В первой статье мы описали различные стадии предобработки исходного изображения паспорта. Сначала из изображения вырезается зона, содержащая 2х2 решетку (подобную шахматной доске) и содержащая 2 шаблона по горизонтали и вертикали. Это может быть сделано (с ошибкой менее с 5%), поскольку физические размеры документа, размеры и период периодических шаблонов фиксированы и известны заранее. Положение региона может быть установлено комбинированием физических координат документа с его координатами на изображении.
Далее производится существенное сжатие и сглаживание изображения для подавления фона и нивелирования различий между периодическими паттернами. Рисунок ниже показывает изображение вырезанного региона Российского паспорта, результаты его предобработки и амплитуду его ДПФ.
 — обработка -->
— обработка -->  — ДПФ -->
— ДПФ --> 
Как и ожидалось, амплитуда ДПФ имеет заметные пики с распределением, похожим на шахматную доску.
В соответствии с моделью изображения, исходное изображение состоит из трех независимых сигналов: фонового изображения) и единичного образца периодического паттерна
и единичного образца периодического паттерна ) , который свертывается со сдвинутым импульсным сигналом
, который свертывается со сдвинутым импульсным сигналом ) , чтобы получить периодический паттерн
, чтобы получить периодический паттерн ) :
:
%20%3D%20h(x)%20%2B%20f(x)%20*%20c(x)%0A)
После выполнения ДПФ на) , мы имеем:
, мы имеем:
%20%3D%20%5Cmathcal%7BF%7D%20h(x)%20%2B%20%5Cmathcal%7BF%7D%20f(x)%20%5Ccdot%20%5Cmathcal%7BF%7D%20c(x)%0A)
Для получения сдвига фаз , хранящегося в
, хранящегося в ) , из
, из ) , которое мы вычислили для данного изображения, нам необходимо постепенно подавить остальные компоненты уравнения.
, которое мы вычислили для данного изображения, нам необходимо постепенно подавить остальные компоненты уравнения.
Если фон) после препроцессинга достаточно однороден на обрабатываемых документах, возможно простое вычисление усредненного спектра
после препроцессинга достаточно однороден на обрабатываемых документах, возможно простое вычисление усредненного спектра ) на изображениях документов, на которых отсутствует искомый периодический паттерн, с последующим его вычитанием из
на изображениях документов, на которых отсутствует искомый периодический паттерн, с последующим его вычитанием из ) .
.
Однако, фоновое изображение) в нашей модели фактически не является фоном в терминах структуры Российского паспорта: оно содержит персональные данные, которые по определению различаются на обрабатываемом наборе.
в нашей модели фактически не является фоном в терминах структуры Российского паспорта: оно содержит персональные данные, которые по определению различаются на обрабатываемом наборе.
Ранее мы уже упоминали тот факт, что ДПФ позиции (частоты) без пиков не содержат полезной информации касательно периодических паттернов, поскольку они представляют фон. Предположив, что) является гладким, мы можем интерполировать его вклад в каждый пик
является гладким, мы можем интерполировать его вклад в каждый пик ) , основываясь на значениях в соседних с пиком позициях. Усредненное значение
, основываясь на значениях в соседних с пиком позициях. Усредненное значение %7D) по
по ) по ближайшим соседям пика
по ближайшим соседям пика %5C%7D) в 3x3 окне является приемлемой оценкой
в 3x3 окне является приемлемой оценкой ) для вычитания из
для вычитания из ) , чтобы вычистить фон:
, чтобы вычистить фон:
%20%5Cleftarrow%20%5Cmathcal%7BF%7D%20I(x%2C%20y)%20-%20%5Coverline%7B%5Cmathcal%7BF%7D%20I(x'%2C%20y')%7D%0A)
Следующий рисунок содержит сжатое изображение и изображение, полученное в результате обратного ДПФ после вычитания интерполированного спектра фона и обнуления ДПФ на всех непиковых частотах.
 — ДПФ, вычитание спектра фона, обратное ДПФ ---->
— ДПФ, вычитание спектра фона, обратное ДПФ ----> 
Как и ожидалось, только периодический паттерн остался на простом монотонном фоне и экземпляры периодическиого паттерна стали более похожими друг на друга. Отметим, что фон не является черным, поскольку значение ДПФ на) , которое содержит усредненное по изображению значение, не было обнулено.
, которое содержит усредненное по изображению значение, не было обнулено.
После удаления фонового спектра у нас осталось%20%5Ccdot%20%5Cmathcal%7BF%7D%20c(x)) . При перемножении двух комплексных чисел, их фазы складываются. Тогда, для достижения фазового угла
. При перемножении двух комплексных чисел, их фазы складываются. Тогда, для достижения фазового угла ) у пика
у пика ) , соответствующий фазовый угол спектра единичного экземпляра периодического паттерна
, соответствующий фазовый угол спектра единичного экземпляра периодического паттерна ) должен быть вычтен.
должен быть вычтен.
Проблема состоит в том, что спектр периодического паттерна, как правило, неизвестен. Одним из возможных решений является экспериментальное вычисление фазы представленного образца паттерна и его последующее вычитание. В наших экспериментах мы использовали другой путь, предполагая, что фазовый вклад) постоянен, значит, к результирующему сдвигу
постоянен, значит, к результирующему сдвигу  добавляется еще один константный сдвиг. Эта сдвиговая константа может быть оценена экспериментально как систематическая ошибка на тестовом наборе данных.
добавляется еще один константный сдвиг. Эта сдвиговая константа может быть оценена экспериментально как систематическая ошибка на тестовом наборе данных.
По окончании предобработки спектра мы имеем фазовый угол импульсного сигнала) , который предположительно содержит всю необходимую информацию про фазовый сдвиг
, который предположительно содержит всю необходимую информацию про фазовый сдвиг %5ET%7D) .
.
Мы можем построить систему уравнений (каждое уравнение соответствует) пику) по модулю
пику) по модулю  :
:

Или, в матричной форме:

В левой части системы содержатся «идеальные» значения фазы, соответствующие пикам, а в правой — актуальные значение фазы ДПФ для данного изображения в позициях пиков.
Эта система переопределена, т.к. она имеет уравнений (по числу рассматриваемых пиков) и только 2 переменные:
уравнений (по числу рассматриваемых пиков) и только 2 переменные:  и
и  . Переопределенные системы уравнений могут быть приближенно решены методом наименьших квадратов (МНК) поиском решения, минимизирующего сумму квадратов невязок. Однако, эта система является системой по модулю
. Переопределенные системы уравнений могут быть приближенно решены методом наименьших квадратов (МНК) поиском решения, минимизирующего сумму квадратов невязок. Однако, эта система является системой по модулю  поэтому напрямую МНК не может быть применен, но мы можем вычислить начальное решение и скорректировать его последовательным решением системы.
поэтому напрямую МНК не может быть применен, но мы можем вычислить начальное решение и скорректировать его последовательным решением системы.
Посмотрим на два уравнения для пиков под номерами) и
и ) :
:

Эта система имеет 4 допустимых решения:) ,
, ) ,
, ) и
и ) . Из-за подобной шахматной доске структуры пиковых паттернов в нашем случае, а также, поскольку
. Из-за подобной шахматной доске структуры пиковых паттернов в нашем случае, а также, поскольку  представляет собой сдвиг на единичный период, первое с четвертым решения идентичны, как и второе с третьим. Остается два потенциальных решения:
представляет собой сдвиг на единичный период, первое с четвертым решения идентичны, как и второе с третьим. Остается два потенциальных решения: %5ET) и
и %5ET) .
.
Для выбора правильного решения мы можем добавить к системе два оставшихся уравнения для пиков) и
и ) , вновь сделав систему переопределенной. Тогда, значение невязки
, вновь сделав систему переопределенной. Тогда, значение невязки  вычисляется для
вычисляется для  -го решения
-го решения  с учетом всех
с учетом всех  уравнений:
уравнений:
%5E2%7D%0A%20%20%20%20%20%20%20%20%20%20%20%3D%20%5Cfrac%7B1%7D%7Bn%7D%7CA%5Cphi%5E*_k-b%7C%5E2%20)
Отметим, что промежуточные вычисления, затрагивающие фазовые углы (вычисление разностей), выполняются в) .
.
Наконец, решение , имеющее наименьшее значение
, имеющее наименьшее значение  выбирается в качестве
выбирается в качестве  , поскольку другое решение будет иметь намного большее значения невязки. Большое значение
, поскольку другое решение будет иметь намного большее значения невязки. Большое значение  для
для  может означать ложное обнаружение пика.
может означать ложное обнаружение пика.
Найденное выше начальное решение могло бы быть хорошим, если бы оставшийся спектр содержал только информацию про) и ничего более. К сожалению, он искажен спектральными составляющими от фона и от образцов периодических паттернов, которые не были полностью удалены во время предобработки.
и ничего более. К сожалению, он искажен спектральными составляющими от фона и от образцов периодических паттернов, которые не были полностью удалены во время предобработки.
На данном этапе выбранное решение является все еще верным, но может быть уточнено с использованием фазовой информации в других пиках, а не только по двум первым. Вычтем
является все еще верным, но может быть уточнено с использованием фазовой информации в других пиках, а не только по двум первым. Вычтем  (используя
(используя  уравнения) из обоих частей системы уравнений, сдвинув таким образом пространство решений по
уравнения) из обоих частей системы уравнений, сдвинув таким образом пространство решений по  и получив следующую переопределенную систему уравнений для корректирующего решения
и получив следующую переопределенную систему уравнений для корректирующего решения  :
:

Предполагая, что в первом приближении решения мы ошиблись не больше, чем на , мы можем не брать систему по модулю
, мы можем не брать систему по модулю  , т.к. после сдвига системы каждое уравнение будет внутри
, т.к. после сдвига системы каждое уравнение будет внутри  , что означает, что мы может приближенно решить систему, используя метод наименьших квадратов. После того, как решение
, что означает, что мы может приближенно решить систему, используя метод наименьших квадратов. После того, как решение  найдено, оно должно быть добавлено к ранее найденному начальному решению
найдено, оно должно быть добавлено к ранее найденному начальному решению  в качестве корректирующего значения.
в качестве корректирующего значения.
До сих пор мы рассматривали уравнения для первых 4 пиков) имеющих
имеющих ) сумму равную 2 (и
сумму равную 2 (и  из-за симметричности ДПФ), но ведь существуют другие пики с суммами, равными 4, 6 и так далее. Причина, почему они не были добавлены ранее, состоит в том, что при увеличении
из-за симметричности ДПФ), но ведь существуют другие пики с суммами, равными 4, 6 и так далее. Причина, почему они не были добавлены ранее, состоит в том, что при увеличении ) увеличивается и количество подходящих решений системы, и тем ближе они становятся друг к другу по модулю
увеличивается и количество подходящих решений системы, и тем ближе они становятся друг к другу по модулю  .
.
Для использования информации о фазовом сдвиге, содержащейся в остальных пиках, мы можем повторить вышеописанный процесс корректировки начального решения, заменив скорректированным решением, полученным для суммы, равной 4 и используя все уравнения, имеющие сумму, равную 6 и так далее, до достижения требуемой точности. Предполагая, что с увеличением итерации ошибка уменьшается, каждое уравнение будет находиться в пределах
скорректированным решением, полученным для суммы, равной 4 и используя все уравнения, имеющие сумму, равную 6 и так далее, до достижения требуемой точности. Предполагая, что с увеличением итерации ошибка уменьшается, каждое уравнение будет находиться в пределах  , что позволяет применять МНК для решения системы.
, что позволяет применять МНК для решения системы.
Теперь, имея фазовый сдвиг) , мы можем легко преобразовать его обратно в пиксельный сдвиг
, мы можем легко преобразовать его обратно в пиксельный сдвиг ) . Зная период и размер паттернов, мы можем восстановить положение каждого паттерна решетки. Размер и положение вырезанного региона, который мы использовали в процессе обработки, также известны, поэтому мы можем получить позиции паттернов на исходном изображении документа.
. Зная период и размер паттернов, мы можем восстановить положение каждого паттерна решетки. Размер и положение вырезанного региона, который мы использовали в процессе обработки, также известны, поэтому мы можем получить позиции паттернов на исходном изображении документа.
Следующий рисунок, который вы уже видели в самом начале статьи, представляет пример нахождения голографического периодического шаблона на российском паспорте.


Рамкой с кружком внутри обозначен результат, найденный после решения системы уравнений. Другими рамками обозначены экстраполированные позиции остальных паттернов.
Мы использовали набор данных из 484 изображений отсканированных российских паспортов, имеющих голографическое заполнение. Для каждого изображения в наборе мы подготовили истиное значение пиксельного сдвига его периодического паттерна. Таблица ниже содержит экспериментальные результаты для этого набора данных с усредненным значением невязки смещения как меры точности.
Ошибка задана в процентах от стороны единичного паттерна. Предобработка состояла из сжатия к размеру 56x58 и морфологической операции замыкания; при решении системы для получения фазового сдвига были рассмотрены уравнений пиков.
уравнений пиков.
Следующий рисунок показывает распределение и
и  ошибок для худшего (слева) и лучшего (справа) метода. Черные ячейки представляют ошибку по
ошибок для худшего (слева) и лучшего (справа) метода. Черные ячейки представляют ошибку по  , а белые – по
, а белые – по  .
.
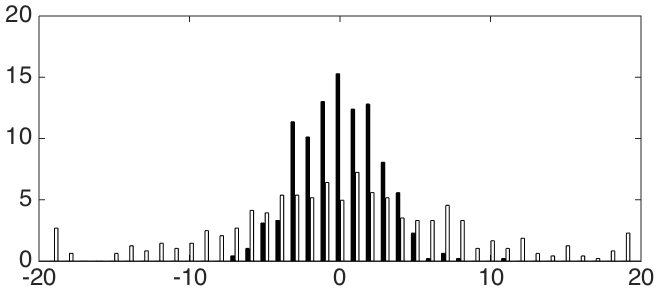
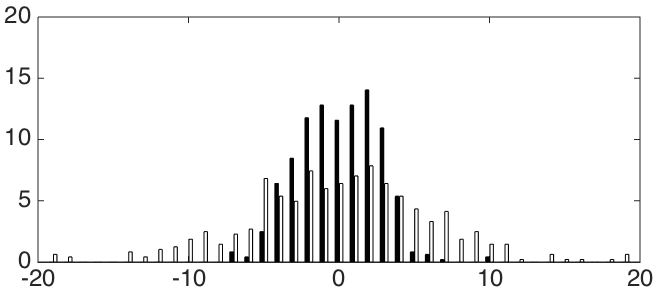
На этих гистограммах ось Y обозначает, сколько процентов изображений (из 484) имеет ошибку, близкую к соответствующему значению по оси X (в процентах от размера стороны периодического паттерна). Видно, что распределение ошибки для лучшего метода менее разбросано, чем для худшего.
ошибки для лучшего метода менее разбросано, чем для худшего.
Мы предложили метод поиска периодических шаблонов на изображениях документов, который использует дискретное преобразование Фурье и показал среднюю ошибку поиска в (от стороны периодического элемента) на наборе из 484 изображений.
(от стороны периодического элемента) на наборе из 484 изображений.
О подробностях применения нами этого метода мы расскажем в одной из следующих статей.


В нашей предыдущей статье по этой теме мы рассказали о первой половине решения задачи поиска — детектировании, т.е. определении наличия периодических элементов на изображении. Сегодня мы расскажем, как найти непосредственное положение периодических элементов на изображении, при условии, что детектирование прошло успешно: мы уверены, что элементы на изображении присутствуют. Вторая часть сильно зависит от первой, поэтому настоятельно рекомендуется сначала ознакомиться с первой, если вы этого еще не сделали.
Как и в прошлый раз, для этого будет использоваться преобразование Фурье.
Модель изображения
Как и в прошлый раз, многие рассуждения будут показаны для одномерного случая, который потом легко переносится на двумерный.
Напомним, что
Так как нам заранее известна структура периодического шаблона (в случае паспорта РФ — размер и период голограмм), для восстановления положения элементов достаточно знать только сдвиг всего шаблона по горизонтали и вертикали, что есть то же самое, что сдвиг одного из “орлов”.
Дискретное преобразование Фурье от сдвинутого периодического шаблона
Сдвиг сигнала паттерна
Предположим, что
Поскольку фазовый угол
Фазовый сдвиг на
На рисунке показан пример ДПФ фазы сдвинутого импульсного сигнала с значениями
А вот так выглядит амплитуда и фаза ДПФ для похожей на шахматную доску сетки Гауссиан:
 — ДПФ -->
— ДПФ --> 

Для двумерного изображения, фазовый сдвиг
Применяя вновь теорему о ДПФ сдвинутого сигнала, можно расширить уравнение сдвига и показать, что фазовый угол
Как и для одномерного случая, для получения сдвинутой фазы
Поиск периодического шаблона
Для определения точного местоположения периодического паттерна достаточно оценить его фазовый сдвиг
Вырезание, масштабирование и предобработка изображения
В первой статье мы описали различные стадии предобработки исходного изображения паспорта. Сначала из изображения вырезается зона, содержащая 2х2 решетку (подобную шахматной доске) и содержащая 2 шаблона по горизонтали и вертикали. Это может быть сделано (с ошибкой менее с 5%), поскольку физические размеры документа, размеры и период периодических шаблонов фиксированы и известны заранее. Положение региона может быть установлено комбинированием физических координат документа с его координатами на изображении.
Далее производится существенное сжатие и сглаживание изображения для подавления фона и нивелирования различий между периодическими паттернами. Рисунок ниже показывает изображение вырезанного региона Российского паспорта, результаты его предобработки и амплитуду его ДПФ.
 — обработка -->
— обработка -->  — ДПФ -->
— ДПФ --> 
Как и ожидалось, амплитуда ДПФ имеет заметные пики с распределением, похожим на шахматную доску.
Предобработка спектра
В соответствии с моделью изображения, исходное изображение состоит из трех независимых сигналов: фонового изображения
После выполнения ДПФ на
Для получения сдвига фаз
Подавление спектра фона
Если фон
Однако, фоновое изображение
Ранее мы уже упоминали тот факт, что ДПФ позиции (частоты) без пиков не содержат полезной информации касательно периодических паттернов, поскольку они представляют фон. Предположив, что
Следующий рисунок содержит сжатое изображение и изображение, полученное в результате обратного ДПФ после вычитания интерполированного спектра фона и обнуления ДПФ на всех непиковых частотах.
 — ДПФ, вычитание спектра фона, обратное ДПФ ---->
— ДПФ, вычитание спектра фона, обратное ДПФ ----> 
Как и ожидалось, только периодический паттерн остался на простом монотонном фоне и экземпляры периодическиого паттерна стали более похожими друг на друга. Отметим, что фон не является черным, поскольку значение ДПФ на
Подавление спектра экземпляров паттерна
После удаления фонового спектра у нас осталось
Проблема состоит в том, что спектр периодического паттерна, как правило, неизвестен. Одним из возможных решений является экспериментальное вычисление фазы представленного образца паттерна и его последующее вычитание. В наших экспериментах мы использовали другой путь, предполагая, что фазовый вклад
Восстановление фазового сдвига
По окончании предобработки спектра мы имеем фазовый угол импульсного сигнала
Мы можем построить систему уравнений (каждое уравнение соответствует
Или, в матричной форме:
В левой части системы содержатся «идеальные» значения фазы, соответствующие пикам, а в правой — актуальные значение фазы ДПФ для данного изображения в позициях пиков.
Эта система переопределена, т.к. она имеет
Вычисление начального решения
Посмотрим на два уравнения для пиков под номерами
Эта система имеет 4 допустимых решения:
Для выбора правильного решения мы можем добавить к системе два оставшихся уравнения для пиков
Отметим, что промежуточные вычисления, затрагивающие фазовые углы (вычисление разностей), выполняются в
Наконец, решение
Корректировка решения
Найденное выше начальное решение могло бы быть хорошим, если бы оставшийся спектр содержал только информацию про
На данном этапе выбранное решение
Предполагая, что в первом приближении решения мы ошиблись не больше, чем на
До сих пор мы рассматривали уравнения для первых 4 пиков
Для использования информации о фазовом сдвиге, содержащейся в остальных пиках, мы можем повторить вышеописанный процесс корректировки начального решения, заменив
Восстановление расположения периодических паттернов
Теперь, имея фазовый сдвиг
Следующий рисунок, который вы уже видели в самом начале статьи, представляет пример нахождения голографического периодического шаблона на российском паспорте.


Рамкой с кружком внутри обозначен результат, найденный после решения системы уравнений. Другими рамками обозначены экстраполированные позиции остальных паттернов.
Экспериментальные результаты
Мы использовали набор данных из 484 изображений отсканированных российских паспортов, имеющих голографическое заполнение. Для каждого изображения в наборе мы подготовили истиное значение пиксельного сдвига его периодического паттерна. Таблица ниже содержит экспериментальные результаты для этого набора данных с усредненным значением невязки смещения как меры точности.
Ошибка задана в процентах от стороны единичного паттерна. Предобработка состояла из сжатия к размеру 56x58 и морфологической операции замыкания; при решении системы для получения фазового сдвига были рассмотрены
| Подавление фона | Корректировка с МНК | x ошибка | y ошибка | Общая ошибка |
|---|---|---|---|---|
| Отсутствует | Отсутствует | 2.13 | 6.40 | 6.75 |
| Присутствует | Отсутствует | 2.09 | 6.04 | 6.40 |
| Отсутствует | Присутствует | 2.19 | 5.05 | 5.50 |
| Присутствует | Присутствует | 2.20 | 4.77 | 5.25 |
Следующий рисунок показывает распределение
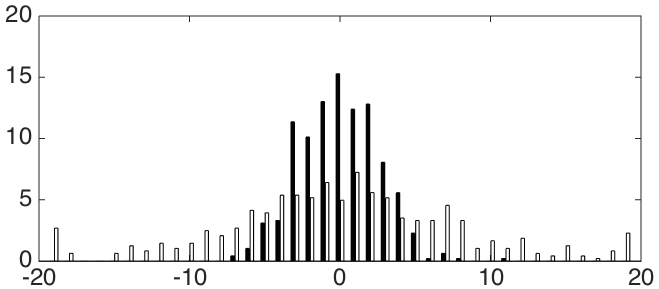
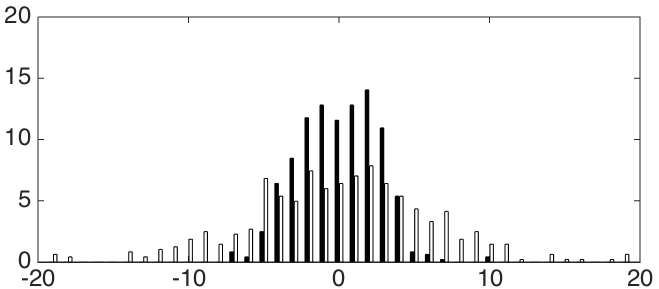
На этих гистограммах ось Y обозначает, сколько процентов изображений (из 484) имеет ошибку, близкую к соответствующему значению по оси X (в процентах от размера стороны периодического паттерна). Видно, что распределение
Заключение
Мы предложили метод поиска периодических шаблонов на изображениях документов, который использует дискретное преобразование Фурье и показал среднюю ошибку поиска в
О подробностях применения нами этого метода мы расскажем в одной из следующих статей.