Привет, Хабр! Сегодня мы очень подробно расскажем о неочевидных моментах в такой, казалось бы, простой операции: исправлении проективных искажений на изображении. Как это часто оказывается в жизни, нам пришлось выбирать, что важнее: качество или скорость. И чтобы достичь некого баланса мы вспомнили об алгоритмах, которые активно исследовали еще в 80-90-е годы в рамках задачи рендеринга структур, и с тех пор редко вспоминали в контексте обработки изображений. Если интересно, заглядывайте под кат!
Модель камеры обскуры, которая на практике неплохо приближает и короткофокусные камеры мобильных телефонов, подсказывает нам что при поворотах камеры изображения плоского объекта связаны между собой проективным преобразованием. Общий вид проективного преобразования такой:
где
матрица проективного преобразования, 
и 
координаты на исходном и преобразованном изображениях.
Проективное преобразование изображения — это одно из возможных геометрических преобразований изображений (таких преобразований, при которых точки исходного изображения переходят в точки конечного изображения согласно определенному закону).
Чтобы разобраться в том, как именно следует решать задачу геометрического преобразования цифрового изображения, нужно учитывать модель его формирования из оптического изображения на матрице камеры. Согласно Г. Уолбергу [1] наш алгоритм должен аппроксимировать следующий процесс:
Оптическое изображение это функция двух переменных определенная на непрерывном множестве точек. Этот процесс сложно воспроизвести напрямую, поскольку нам придется аналитически задать вид оптического изображения и его обрабатывать. Для упрощения этого процесса обычно используют метод обратного отображения (англ. reverse mapping):
Здесь 3 шаг соответствует восстановлению оптического изображения, а 1 и 4-й — дискретизации.
Здесь мы рассмотрим только простые виды интерполяции — те, которые можно представить в виде свертки изображения с интерполяционным ядром. В контексте обработки изображений лучше бы подошли алгоритмы адаптивной интерполяции, которые сохраняют четкие границы объектов, однако их вычислительная сложность существенно выше и потому нам не интересна.
Будем рассматривать следующие методы интерполяции:
Еще у интерполяции есть такой важный параметр как точность. Если мы примем, что цифровое изображение получено из оптического методом точечной выборки в центре пикселя и поверим в то, что исходное изображение было непрерывным, то идеальной функцией восстановления будет фильтр низких частот с частотой ½ (см. теорему Котельникова).
Поэтому сравним Фурье-спектры наших ядер интерполяции с фильтром низких частот (на рисунках представлены для одномерного случая).
И что, можно просто взять ядро с достаточно хорошим спектром и получить относительно точные результаты? На самом деле нет, потому что выше мы сделали два допущения: о том что есть значение пикселя изображения и о непрерывности этого изображения. При этом ни то ни другое не является частью хорошей модели формирования изображения, ведь датчики на матрице камеры не точечные, а на изображении очень много информации несут границы объектов — разрывы. Поэтому, увы, следует понимать, что результат интерполяции всегда будет отличаться от оригинального оптического изображения.
Но делать что-то все-таки нужно, поэтому коротко опишем достоинства и недостатки каждого из рассматриваемых методов с практической точки зрения. Проще всего это увидеть при увеличении масштаба изображения (в данном примере — в 10 раз).
Самая простая и самая быстрая, однако она приводит к сильным артефактам.
Лучше по качеству, но требует больше вычислений и вдобавок размывает границы объектов.
Еще лучше в непрерывных областях, но на границе возникает эффект гало (более темная полоса вдоль темного края границы и светлая вдоль светлого). Чтобы избежать такого эффекта нужно использовать неотрицательное ядро свертки например кубический b-сплайн.
У b-сплайна очень узкий спектр, что означает сильное “размытие” изображение (но и хорошее шумоподавление, что может быть полезно).
Такой сплайн требует оценки частных производных в каждом пикселе изображения. Если для приближения мы выберем 2-точечную разностную схему то мы получим ядро бикубической интерполяции, поэтому тут мы используем 4-точечную.
Сравним эти методы также по числу обращений в память (числу пикселей исходного изображения для интерполяции в одной точке) и по числу операций умножения на точку.
Видно, что последние 3 способа существенно более вычислительно затратные, чем первые 2.
Это тот самый шаг, которому совершенно незаслуженно уделяется очень мало внимания в последнее время. Самый простой способ произвести проективное преобразование изображения — оценить значение каждого пикселя конечного изображения по значению, которое получается при обратном преобразовании его центра на плоскость исходного изображения (с учетом выбранного метода интерполяции). Такой подход назовем попиксельной дискретизацией. Однако в областях, где изображение сжимается, это может привести к существенным артефактам, вызванным проблемой наложения спектров при недостаточной частоте дискретизации.
Наглядно продемонстрируем артефакты сжатия на образце паспорта РФ и отдельном его поле — место рождения (гор. Архангельск), сжатым с помощью попиксельной дискретизации или алгоритма FAST, который мы рассмотрим ниже.
Видно, что текст на левом изображении стал нечитаемым. Правильно, ведь мы берем всего одну точку из целого региона исходного изображения!
Раз нам не удалось выполнить оценку по одному пикселю, то почему бы не выбрать больше отсчетов на пиксель, а полученные значения усреднить? Такой подход называется суперсемплинг. Он действительно увеличивает качество, но вместе с тем и вычислительная сложность возрастает пропорционально числу отсчетов на пиксель.
Более вычислительно эффективные методы были придуманы в конце прошлого века, когда в компьютерной графике решалась задача рендеринга текстур, наложенных на плоские объекты. Одним из таких методов является преобразование с помощью mip-map структуры. Mip-map это пирамида изображений состоящая из самого исходного изображения, а также его копий уменьшенных в 2, 4, 8 и так далее раз. Для каждого пикселя мы оцениваем, какая степень сжатия для него характерна, и в соответствие с этой степенью выбираем нужный уровень из пирамиды, в качестве исходного изображения. Есть разные способы оценивать подходящий уровень mip-map (см. подробнее [2]). Здесь мы воспользуемся методом, на основе оценки частных производных по известной матрице проективного преобразования. Однако чтобы избежать артефактов в тех областях конечного изображения, где один уровень mip-map структуры переходит в другой, обычно используют линейную интерполяцию между двумя соседними уровнями пирамиды (это не сильно увеличивает вычислительную сложность, ведь координаты точек на соседних уровнях однозначно связаны).
Однако mip-map никак не учитывает тот факт, что сжатие изображения может быть анизотропным (вытянутым вдоль какого-то направления). Частично эту проблему позволяет решить rip-map. Структура в которой независимо хранятся изображения сжатые в
раз по горизонтали и 
раз по вертикали. В этом случае, после определения коэффициентов сжатия по горизонтали и по вертикали в данной точке конечного изображения, производится интерполяция между результатами с 4, сжатых в нужное число раз, копий исходного изображения. Но и этот метод не идеален, ведь он не учитывает, что направление анизотропии отличаться от направлений, параллельных границам исходного изображения.
Частично эту проблему позволяет решить алгоритм FAST (Footprint Area Sampled Texturing) [3]. Он объединяет идеи mip-map-а и суперсэмплинга. Мы оцениваем степень сжатия исходя из оси наименьшей анизотропии и выбираем число отсчетов пропорционально отношению длин наименьшей оси к наибольшей.
Прежде чем сравнивать эти подходы по вычислительной сложности, оговоримся, что в целях ускорения подсчета обратного проективного преобразования, рационально сделать следующую замену:
где
, 
— матрица обратного проективного преобразования. Так как 
и 
функции одного аргумента мы можем их пред-подсчитать за пропорциональное линейному размеру изображения время. Тогда для вычисления координат прообраза одной точки конечного изображения , потребуется только 1 деление и 2 умножения. Аналогичный трюк можно провернуть с частными производными, которые используются для определения уровня в mip-map или rip-map структуре.
Теперь мы готовы сравнить результаты по вычислительной сложности.
И сравнить визуально (слева направо попиксельная дискретизация, суперсемплиг по 49 отсчетам, mip-map, rip-map, FAST).
А теперь, давайте сравним наши результаты экспериментально. Составим алгоритм проективного преобразования сочетающий каждый из 5 методов интерполяции и 5 методов дискретизации (всего 25 вариантов). Возьмем 20 изображений документов обрезанных до размера 512x512 пикселей, сгенерируем 10 наборов из 3-х матриц проективного преобразования, таких что каждый набор в целом эквивалентен тождественному преобразованию и будем сравнивать PSNR между исходным изображением и преобразованным. Напомним что PSNR это
, где 
это максимум по исходному изображению а 
— среднеквадратичное отклонение конечного от исходного. Чем больше PSNR тем лучше. Так же будем замерять время работы проективного преобразования на ODROID-XU4 с процессором ARM Cortex-A15 (2000 MHz и 2GB RAM).
Чудовищная таблица с результатами:
Если хочется хорошего качества при не слишком низкой скорости работы, стоит подумать про билинейную интерполяцию в сочетании с дискретизацией с помощью mip-map-а или FAST. Однако если доподлинно известно, что проективное искажение очень слабое, для увеличения скорости можно использовать попиксельную дискретизацию в паре с билинейной интерполяцией или же даже интерполяцией по ближайшему пикселю. А если нужно высокое качество и не сильно ограничено время работы, можно использовать бикубическую или адаптивную интерполяцию в паре с умеренным суперсемплингом (например также адаптивным, зависящим от локального коэффициента сжатия).
P.S. Публикация подготовлена на основе доклада: A. Trusov and E. Limonova, “The analysis of projective transformation algorithms for image recognition on mobile devices,” ICMV 2019, 11433 ed., Wolfgang Osten, Dmitry Nikolaev, Jianhong Zhou, Ed., SPIE, Jan. 2020, vol. 11433, ISSN 0277-786X, ISBN 978-15-10636-43-9, vol. 11433, 11433 0Y, pp. 1-8, 2020, DOI: 10.1117/12.2559732.
Модель камеры обскуры, которая на практике неплохо приближает и короткофокусные камеры мобильных телефонов, подсказывает нам что при поворотах камеры изображения плоского объекта связаны между собой проективным преобразованием. Общий вид проективного преобразования такой:
где
матрица проективного преобразования, и координаты на исходном и преобразованном изображениях.Геометрическое преобразование изображений
Проективное преобразование изображения — это одно из возможных геометрических преобразований изображений (таких преобразований, при которых точки исходного изображения переходят в точки конечного изображения согласно определенному закону).
Чтобы разобраться в том, как именно следует решать задачу геометрического преобразования цифрового изображения, нужно учитывать модель его формирования из оптического изображения на матрице камеры. Согласно Г. Уолбергу [1] наш алгоритм должен аппроксимировать следующий процесс:
- Восстановление оптического изображения из цифрового.
- Геометрическое преобразование оптического изображения.
- Дискретизация (англ. sampling) преобразованного изображения.
Оптическое изображение это функция двух переменных определенная на непрерывном множестве точек. Этот процесс сложно воспроизвести напрямую, поскольку нам придется аналитически задать вид оптического изображения и его обрабатывать. Для упрощения этого процесса обычно используют метод обратного отображения (англ. reverse mapping):
- На плоскости конечного изображения выбирается сетка отсчетов (англ. sampling grid) — точек, по которым мы будем оценивать значения пикселей конечного изображения (это может быть центр каждого пикселя, а может быть несколько точек на пиксель).
- С помощью обратного геометрического преобразования эта сетка переносится в пространство исходного изображения.
- Для каждого отсчета сетки оценивается его значение. Поскольку он не обязательно окажется в точке с целыми координатами, нам потребуется некоторая интерполяция значения изображения, например, интерполяция по соседним пикселям.
- По отчетам сетки оцениваем значения пикселей конечного изображения.
Здесь 3 шаг соответствует восстановлению оптического изображения, а 1 и 4-й — дискретизации.
Интерполяция
Здесь мы рассмотрим только простые виды интерполяции — те, которые можно представить в виде свертки изображения с интерполяционным ядром. В контексте обработки изображений лучше бы подошли алгоритмы адаптивной интерполяции, которые сохраняют четкие границы объектов, однако их вычислительная сложность существенно выше и потому нам не интересна.
Будем рассматривать следующие методы интерполяции:
- по ближайшему пикселю,
- билинейную,
- бикубическую,
- кубическим b-сплайном,
- кубическим эрмитовым сплайном, по 36 точкам.
Еще у интерполяции есть такой важный параметр как точность. Если мы примем, что цифровое изображение получено из оптического методом точечной выборки в центре пикселя и поверим в то, что исходное изображение было непрерывным, то идеальной функцией восстановления будет фильтр низких частот с частотой ½ (см. теорему Котельникова).
Поэтому сравним Фурье-спектры наших ядер интерполяции с фильтром низких частот (на рисунках представлены для одномерного случая).
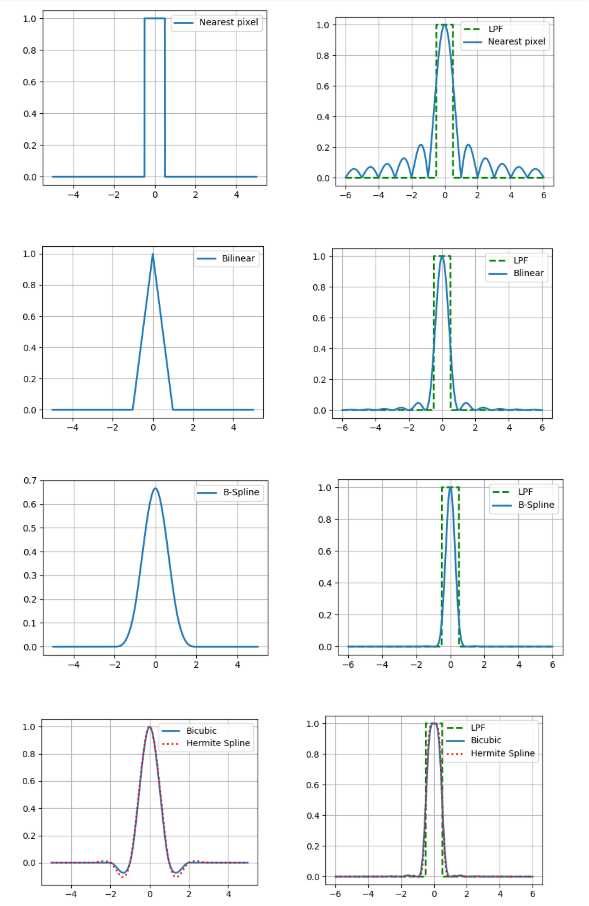
И что, можно просто взять ядро с достаточно хорошим спектром и получить относительно точные результаты? На самом деле нет, потому что выше мы сделали два допущения: о том что есть значение пикселя изображения и о непрерывности этого изображения. При этом ни то ни другое не является частью хорошей модели формирования изображения, ведь датчики на матрице камеры не точечные, а на изображении очень много информации несут границы объектов — разрывы. Поэтому, увы, следует понимать, что результат интерполяции всегда будет отличаться от оригинального оптического изображения.
Но делать что-то все-таки нужно, поэтому коротко опишем достоинства и недостатки каждого из рассматриваемых методов с практической точки зрения. Проще всего это увидеть при увеличении масштаба изображения (в данном примере — в 10 раз).
Интерполяция по ближайшему пикселю
Самая простая и самая быстрая, однако она приводит к сильным артефактам.
Билинейная интерполяция
Лучше по качеству, но требует больше вычислений и вдобавок размывает границы объектов.
Бикубическая интерполяция
Еще лучше в непрерывных областях, но на границе возникает эффект гало (более темная полоса вдоль темного края границы и светлая вдоль светлого). Чтобы избежать такого эффекта нужно использовать неотрицательное ядро свертки например кубический b-сплайн.
Интерполяция B-сплайном
У b-сплайна очень узкий спектр, что означает сильное “размытие” изображение (но и хорошее шумоподавление, что может быть полезно).
Итерполяция на основе кубического Эрмитового сплайна
Такой сплайн требует оценки частных производных в каждом пикселе изображения. Если для приближения мы выберем 2-точечную разностную схему то мы получим ядро бикубической интерполяции, поэтому тут мы используем 4-точечную.
Сравним эти методы также по числу обращений в память (числу пикселей исходного изображения для интерполяции в одной точке) и по числу операций умножения на точку.
| Интерполяция | Число пикселей | Число умножений |
| По ближайшему | 1 | 0 |
| Билинейная | 4 | 8 |
| Бикубическая | 16 | 68 |
| B-сплайн | 16 | 68 |
| Эрмитов сплайн | 36 | 76 |
Видно, что последние 3 способа существенно более вычислительно затратные, чем первые 2.
Дискретизация
Это тот самый шаг, которому совершенно незаслуженно уделяется очень мало внимания в последнее время. Самый простой способ произвести проективное преобразование изображения — оценить значение каждого пикселя конечного изображения по значению, которое получается при обратном преобразовании его центра на плоскость исходного изображения (с учетом выбранного метода интерполяции). Такой подход назовем попиксельной дискретизацией. Однако в областях, где изображение сжимается, это может привести к существенным артефактам, вызванным проблемой наложения спектров при недостаточной частоте дискретизации.
Наглядно продемонстрируем артефакты сжатия на образце паспорта РФ и отдельном его поле — место рождения (гор. Архангельск), сжатым с помощью попиксельной дискретизации или алгоритма FAST, который мы рассмотрим ниже.
Видно, что текст на левом изображении стал нечитаемым. Правильно, ведь мы берем всего одну точку из целого региона исходного изображения!
Раз нам не удалось выполнить оценку по одному пикселю, то почему бы не выбрать больше отсчетов на пиксель, а полученные значения усреднить? Такой подход называется суперсемплинг. Он действительно увеличивает качество, но вместе с тем и вычислительная сложность возрастает пропорционально числу отсчетов на пиксель.
Более вычислительно эффективные методы были придуманы в конце прошлого века, когда в компьютерной графике решалась задача рендеринга текстур, наложенных на плоские объекты. Одним из таких методов является преобразование с помощью mip-map структуры. Mip-map это пирамида изображений состоящая из самого исходного изображения, а также его копий уменьшенных в 2, 4, 8 и так далее раз. Для каждого пикселя мы оцениваем, какая степень сжатия для него характерна, и в соответствие с этой степенью выбираем нужный уровень из пирамиды, в качестве исходного изображения. Есть разные способы оценивать подходящий уровень mip-map (см. подробнее [2]). Здесь мы воспользуемся методом, на основе оценки частных производных по известной матрице проективного преобразования. Однако чтобы избежать артефактов в тех областях конечного изображения, где один уровень mip-map структуры переходит в другой, обычно используют линейную интерполяцию между двумя соседними уровнями пирамиды (это не сильно увеличивает вычислительную сложность, ведь координаты точек на соседних уровнях однозначно связаны).
Однако mip-map никак не учитывает тот факт, что сжатие изображения может быть анизотропным (вытянутым вдоль какого-то направления). Частично эту проблему позволяет решить rip-map. Структура в которой независимо хранятся изображения сжатые в
раз по горизонтали и раз по вертикали. В этом случае, после определения коэффициентов сжатия по горизонтали и по вертикали в данной точке конечного изображения, производится интерполяция между результатами с 4, сжатых в нужное число раз, копий исходного изображения. Но и этот метод не идеален, ведь он не учитывает, что направление анизотропии отличаться от направлений, параллельных границам исходного изображения.Частично эту проблему позволяет решить алгоритм FAST (Footprint Area Sampled Texturing) [3]. Он объединяет идеи mip-map-а и суперсэмплинга. Мы оцениваем степень сжатия исходя из оси наименьшей анизотропии и выбираем число отсчетов пропорционально отношению длин наименьшей оси к наибольшей.
Прежде чем сравнивать эти подходы по вычислительной сложности, оговоримся, что в целях ускорения подсчета обратного проективного преобразования, рационально сделать следующую замену:
где
, — матрица обратного проективного преобразования. Так как и функции одного аргумента мы можем их пред-подсчитать за пропорциональное линейному размеру изображения время. Тогда для вычисления координат прообраза одной точки конечного изображения , потребуется только 1 деление и 2 умножения. Аналогичный трюк можно провернуть с частными производными, которые используются для определения уровня в mip-map или rip-map структуре.Теперь мы готовы сравнить результаты по вычислительной сложности.
| Метод | Число отсчетов на пиксель | Число умножений на отсчет | Дополнительная память для структур (в долях исходного изображения) |
| Попиксельная дискретизация | 1 | 2 | 0 |
| Суперсемплинг | n | 2 | 0 |
| Mip-map | 2 | 7 | 1/3 |
| Rip-map | 4 | 7 | 3 |
| Fast | <= n | 7 | 1/3 |
И сравнить визуально (слева направо попиксельная дискретизация, суперсемплиг по 49 отсчетам, mip-map, rip-map, FAST).
Эксперимент
А теперь, давайте сравним наши результаты экспериментально. Составим алгоритм проективного преобразования сочетающий каждый из 5 методов интерполяции и 5 методов дискретизации (всего 25 вариантов). Возьмем 20 изображений документов обрезанных до размера 512x512 пикселей, сгенерируем 10 наборов из 3-х матриц проективного преобразования, таких что каждый набор в целом эквивалентен тождественному преобразованию и будем сравнивать PSNR между исходным изображением и преобразованным. Напомним что PSNR это
, где это максимум по исходному изображению а — среднеквадратичное отклонение конечного от исходного. Чем больше PSNR тем лучше. Так же будем замерять время работы проективного преобразования на ODROID-XU4 с процессором ARM Cortex-A15 (2000 MHz и 2GB RAM).Чудовищная таблица с результатами:
| Дискретизация |
Интерполяция |
Время (сек.) |
PSNR (дБ) |
| Попиксельная |
По ближайшему |
0.074 |
23.1 |
| Билинейная |
0.161 |
25.4 |
|
| Бикубическая |
0.496 |
26.0 |
|
| B-сплайн |
0.517 |
24.8 |
|
| Эрмитов сплайн |
0.978 |
26.2 |
|
| Суперсемплинг (x49) |
По ближайшему |
4.01 |
25.6 |
| Билинейная |
7.76 |
25.3 |
|
| Бикубическая |
23.7 |
26.1 |
|
| B-сплайн |
24.7 |
24.6 |
|
| Эрмитов сплайн |
46.9 |
26.2 |
|
| Mip-map |
По ближайшему |
0.194 |
24.0 |
| Билинейная |
0.302 |
24.6 |
|
| Бикубическая |
0.770 |
25.3 |
|
| B-сплайн |
0.800 |
23.9 |
|
| Эрмитов сплайн |
1.56 |
25.5 |
|
| Rip-map |
По ближайшему |
0.328 |
24.2 |
| Билинейная |
0.510 |
25.0 |
|
| Бикубическая |
1.231 |
25.8 |
|
| B-сплайн |
1.270 |
24.2 |
|
| Эрмитов сплайн |
2.41 |
25.8 |
|
| FAST |
По ближайшему |
0.342 |
24.0 |
| Билинейная |
0.539 |
25.2 |
|
| Бикубическая |
1.31 |
26.0 |
|
| B-сплайн |
1.36 |
24.4 |
|
| Эрмитов сплайн |
2.42 |
26.2 |
Какие можно сделать выводы?
- Использование интерполяции по ближайшему пикселю или попиксельной дискретизации приводит к низкому качеству (было очевидно еще по примерам выше).
- Интерполяция полиномами Эрмита по 36 точкам или суперсэмплинг — вычислительно затратные методы.
- Использование бикубической или b-сплайновой интерполяции с любым методом дискретизации, кроме попиксельной, также занимает достаточно много времени.
- Rip-map по времени работы сопоставим с FAST при этом качество у него несколько хуже, а дополнительной памяти он привлекает в 9 раз больше (выбор очевиден, да?).
- Дискретизация с помощью mip-map и интерполяция b-сплайном продемонстрировали низкий PSNR поскольку вызывают относительно сильное размытие изображения, что не всегда является такой уж серьезной проблемой.
Если хочется хорошего качества при не слишком низкой скорости работы, стоит подумать про билинейную интерполяцию в сочетании с дискретизацией с помощью mip-map-а или FAST. Однако если доподлинно известно, что проективное искажение очень слабое, для увеличения скорости можно использовать попиксельную дискретизацию в паре с билинейной интерполяцией или же даже интерполяцией по ближайшему пикселю. А если нужно высокое качество и не сильно ограничено время работы, можно использовать бикубическую или адаптивную интерполяцию в паре с умеренным суперсемплингом (например также адаптивным, зависящим от локального коэффициента сжатия).
P.S. Публикация подготовлена на основе доклада: A. Trusov and E. Limonova, “The analysis of projective transformation algorithms for image recognition on mobile devices,” ICMV 2019, 11433 ed., Wolfgang Osten, Dmitry Nikolaev, Jianhong Zhou, Ed., SPIE, Jan. 2020, vol. 11433, ISSN 0277-786X, ISBN 978-15-10636-43-9, vol. 11433, 11433 0Y, pp. 1-8, 2020, DOI: 10.1117/12.2559732.
Список используемых источников
- G. Wolberg, Digital image warping, vol. 10662, IEEE computer society press Los Alamitos, CA (1990).
- J. P. Ewins, M. D. Waller, M. White, and P. F. Lister, “Mip-map level selection for texture mapping,” IEEE Transactions on Visualization and Computer Graphics4(4), 317–329 (1998).
- B. Chen, F. Dachille, and A. E. Kaufman, “Footprint area sampled texturing,” IEEE Transactions on Visualizationand Computer Graphics10(2), 230–240 (2004).
