Составили для вас подборку книг, которые помогут прокачать полезные для работы скиллы и узнать что-то новое, не делая над собой титанических усилий.
Саймон Сингх. «Симпсоны и их математические секреты»
Одна из лучших научно-популярных книг по математике, читать ее легко и приятно.
Автор рассказывает про эпизоды мультсериала «Симпсоны» (и немного про «Футураму»), в которых фигурируют различные математические идеи, понятия и формулы. По всей видимости, создатель обоих сериалов Мэтт Грейнинг (Википедия утверждает, что его фамилия произносится именно так) увлекается математикой и с удовольствием вставляет в эпизоды математические шутки и парадоксы.
В книге много шуток про теорему Ферма, гомеоморфные фигуры, плотность Вселенной, саберметрику, простые числа Софи Жермен, совершенные числа, самовлюблённые числа, стратегию победы в камень-ножницы-бумага, нетранзитивные игральные кости, парадокс «Гранд-отель», гипотезу Страшилы, числа е и π, ряд Эйлера, многомерные пространства и многое другое.
Если математика (или «Симпсоны») вам хоть немного интересны, вы, как и я, получите удовольствие от прочтения.
Грейди Клейн и Алан Дебни. «Статистика. Базовый курс в комиксах»
Я часто читаю аналитические отчеты по информационной безопасности. При этом я уделяю особое внимание методологии исследования, описанию границ и допущений, проверяю и перепроверяю выводы. К сожалению, иногда в них встречаются логические ошибки, подмены понятий, сверхобобщения и другие случайные или умышленные искажения.
Эта книга интересна формой подачи материала, забавными примерами, и, в целом, хорошим и простым объяснением сложных понятий и формул, используемых в статистике. Она помогает лучше понимать, что стоит за данными различных отчетов, опросов и исследований. Книга учит обнаруживать ошибки и манипуляции в статистических выкладках, а значит, критически воспринимать информацию и понимать, стоит ли ей доверять.
«Как лгать при помощи статистики» Дарелла Хаффа – это, пожалуй, одной из самых полезных книг на тему понимания количественных исследований. Это далеко не новинка, книга была впервые издана в 1954 году, но актуальности не теряет до сих пор.
Мне очень нравится, что каждый способ манипуляции статистикой проиллюстрирован на реальном примере. Как правило, рассматриваются искажения в результатах тех или иных исследований, причем очень разного уровня значимости – от качества зубной пасты до эффективности вакцины от полиомиелита.
Такой подход позволяет быстро и практически незаметно для себя усвоить значение и значимость таких приемов.
К сожалению, книга не очень хорошо структурирована, поэтому самостоятельно даю перечень описываемых в ней уловок:
Анхельс Наварро. «Память не изменяет»
Книга, как это понятно из названия, рассказывает о том, как развивать и тренировать память.
В первой части автор дает немного теории, позволяющей лучше понять, как устроена память: на какие виды и фазы ее подразделяют, каковы ее физиологические основы, а также говорит о том, что с ней происходит по мере старения человека и способах этого избежать.
Примерно 2/3 книги отведены собственно практическим советам (вплоть до питания), а также упражнениям. Выполнять их интересно, и, на мой взгляд, достаточно регулярно выделять на это полчаса, чтобы в скором времени заметить прогресс.
Сами упражнения, например, такие:
Андрей Шапенко. «Комиксы про мироустройство. Как понять этот мир, прокачать себя и добиться всего, чего захочешь».
Несмотря на отвратительно пафосное название, книга действительно очень приятная. В ней практически нет «воды», она легко читается и отлично структурирована.
Ее идеи нельзя назвать прорывными, скорее, это набор хорошо сформулированных рациональных подходов к жизненным этапам/вопросам, которые часто пугают людей, мешая двигаться вперед.
Вот вам пара цитат, чтобы было понятнее, что я имею в виду:
«Сразу же узнать, что ты хочешь от жизни, куда движешься, очень проблематично. Дело в том, что сегодня у тебя может не хватать знаний и опыта для того, чтобы увидеть тот образ будущего, где тебе хотелось бы оказаться. Пробуя разные вещи, ты начинаешь отличать свое от чужого и понимаешь, что тебе действительно по душе. Не знаешь, куда ты идешь, не стыдно. Стыдно сидеть и ничего не делать, страдая от бессмысленности и тщетности бытия. Пусть твоей целью на сегодня станет просто новый путь, а потом уже разберешься».
«Если каждый день улучшать какое-то дело всего на 1%, то через год твоя эффективность в нем повысится в 38 раз. Если делать на 1% хуже, то она практически обнулится».
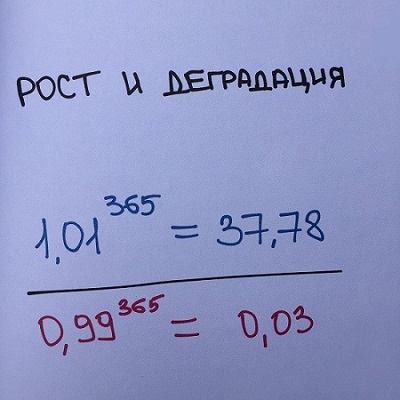
Повторюсь, хотя вы, скорее всего, не найдете в книге фантастических откровений, но если в новом году вас ждут перемены, она поможет избавиться от связанных с ними иррациональных страхов.
Успехов вам в наступившем году!
Саймон Сингх. «Симпсоны и их математические секреты»
Одна из лучших научно-популярных книг по математике, читать ее легко и приятно.
Автор рассказывает про эпизоды мультсериала «Симпсоны» (и немного про «Футураму»), в которых фигурируют различные математические идеи, понятия и формулы. По всей видимости, создатель обоих сериалов Мэтт Грейнинг (Википедия утверждает, что его фамилия произносится именно так) увлекается математикой и с удовольствием вставляет в эпизоды математические шутки и парадоксы. В книге много шуток про теорему Ферма, гомеоморфные фигуры, плотность Вселенной, саберметрику, простые числа Софи Жермен, совершенные числа, самовлюблённые числа, стратегию победы в камень-ножницы-бумага, нетранзитивные игральные кости, парадокс «Гранд-отель», гипотезу Страшилы, числа е и π, ряд Эйлера, многомерные пространства и многое другое.
Если математика (или «Симпсоны») вам хоть немного интересны, вы, как и я, получите удовольствие от прочтения.
Грейди Клейн и Алан Дебни. «Статистика. Базовый курс в комиксах»
Я часто читаю аналитические отчеты по информационной безопасности. При этом я уделяю особое внимание методологии исследования, описанию границ и допущений, проверяю и перепроверяю выводы. К сожалению, иногда в них встречаются логические ошибки, подмены понятий, сверхобобщения и другие случайные или умышленные искажения. Эта книга интересна формой подачи материала, забавными примерами, и, в целом, хорошим и простым объяснением сложных понятий и формул, используемых в статистике. Она помогает лучше понимать, что стоит за данными различных отчетов, опросов и исследований. Книга учит обнаруживать ошибки и манипуляции в статистических выкладках, а значит, критически воспринимать информацию и понимать, стоит ли ей доверять.
Дарелл Хафф. «Как лгать при помощи статистики»
«Как лгать при помощи статистики» Дарелла Хаффа – это, пожалуй, одной из самых полезных книг на тему понимания количественных исследований. Это далеко не новинка, книга была впервые издана в 1954 году, но актуальности не теряет до сих пор. Мне очень нравится, что каждый способ манипуляции статистикой проиллюстрирован на реальном примере. Как правило, рассматриваются искажения в результатах тех или иных исследований, причем очень разного уровня значимости – от качества зубной пасты до эффективности вакцины от полиомиелита.
Такой подход позволяет быстро и практически незаметно для себя усвоить значение и значимость таких приемов.
К сожалению, книга не очень хорошо структурирована, поэтому самостоятельно даю перечень описываемых в ней уловок:
- Необъективная выборка.
- Слишком маленькая выборка, которая могла дать случайный результат.
- Подмена объекта исследования.
- Грамотно выбранное среднее значение («лучшее» из одного: среднее арифметическое, медиана или мода).
- Игнорирование погрешности и вероятности ошибок.
- Использование псевдообоснованных цифр.
- Нарушение причинно-следственной связи.
- «Игры» с масштабом графиков, подписью осей и другим визуальным оформлением результатов.
- Представление величин в виде картинок, на восприятие которых сильно влияет их площадь. При этом разница величин представлена в виде разницы в высоте изображений.
- «Игры» с процентами (некорректное сложение, выбор удобного начального) и т.д.
Анхельс Наварро. «Память не изменяет»
Книга, как это понятно из названия, рассказывает о том, как развивать и тренировать память.
В первой части автор дает немного теории, позволяющей лучше понять, как устроена память: на какие виды и фазы ее подразделяют, каковы ее физиологические основы, а также говорит о том, что с ней происходит по мере старения человека и способах этого избежать.
Примерно 2/3 книги отведены собственно практическим советам (вплоть до питания), а также упражнениям. Выполнять их интересно, и, на мой взгляд, достаточно регулярно выделять на это полчаса, чтобы в скором времени заметить прогресс.
Сами упражнения, например, такие:
Андрей Шапенко. «Комиксы про мироустройство. Как понять этот мир, прокачать себя и добиться всего, чего захочешь».
Несмотря на отвратительно пафосное название, книга действительно очень приятная. В ней практически нет «воды», она легко читается и отлично структурирована.
Ее идеи нельзя назвать прорывными, скорее, это набор хорошо сформулированных рациональных подходов к жизненным этапам/вопросам, которые часто пугают людей, мешая двигаться вперед.
Вот вам пара цитат, чтобы было понятнее, что я имею в виду:
«Сразу же узнать, что ты хочешь от жизни, куда движешься, очень проблематично. Дело в том, что сегодня у тебя может не хватать знаний и опыта для того, чтобы увидеть тот образ будущего, где тебе хотелось бы оказаться. Пробуя разные вещи, ты начинаешь отличать свое от чужого и понимаешь, что тебе действительно по душе. Не знаешь, куда ты идешь, не стыдно. Стыдно сидеть и ничего не делать, страдая от бессмысленности и тщетности бытия. Пусть твоей целью на сегодня станет просто новый путь, а потом уже разберешься».
«Если каждый день улучшать какое-то дело всего на 1%, то через год твоя эффективность в нем повысится в 38 раз. Если делать на 1% хуже, то она практически обнулится».
Повторюсь, хотя вы, скорее всего, не найдете в книге фантастических откровений, но если в новом году вас ждут перемены, она поможет избавиться от связанных с ними иррациональных страхов.
Успехов вам в наступившем году!
